国土二调应用坐标系统转换方法与精度分析

王丽男，杨帆

(辽宁工程技术大学测绘与地理科学学院，辽宁阜新 123000)

1 引言

第二次全国土地调查(以下简称二调)作为一项重大的国情国力调查，目的是全面查清目前全国土地利用现状，掌握真实的土地基础数据，实现土地资源信息的社会化服务。随着时间的推移和土地利用的变化，我国在土地详查图件更新中采用了大量1980西安(以下简称西安80)坐标系下的地形图。为了实现国土二调数据成果的共享和全国性无缝拼接、做到不重不漏，国土部要求各地已有的成果库统一在西安80坐标系框架之下，因此，面临着大量的坐标转换问题。

目前解决这一问题最常用的方法是七参数法但是这种方法存在精度低且不均等的问题。随着测量技术的不断发展，测量界正在不断地探索寻求利用九参数法来解决这一问题。本文主要针对将1954年北京(以下简称北京54)坐标系与西安80坐标系下的平面坐标的转化，分别利用七参数法和九参数法实现，将其所得结果进行精度评定和比较分析。

2 坐标系统转换的方法

人们为了描述空间位置，采用了多种方法，从而也产生了不同的坐标系。在我国通常采用的是北京54坐标系、西安80坐标系或地方局部坐标系等参心坐标系。表1给出了北京54、西安80坐标系的椭球参数，可见两个椭球形状是不同的。

北京54、西安80坐标系的椭球参数 表1

2.1 七参数法

如图1所示，以椭球体中心O为原点，起始子午面与赤道面交线为X轴，在赤道面上与X轴正交的方向为Y轴，椭球体的旋转轴为Z轴，构成右手坐标系O－XYZ［1］。

图1 空间直角坐标系

通过平移旋转和缩放可以实现坐标系基准之间的转换。该法假设坐标基准转换过程中3个坐标轴的缩放因子相同，然后引入3个平移参数、3个旋转参数和1个尺度比参数共7个参数实现空间直角坐标基准的转换。

Brusa－wolf模型为:

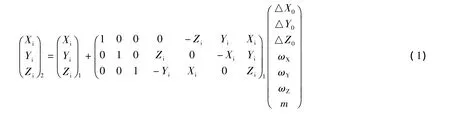
式中:Xi，Yi，Zi分别表示点在空间直角坐标系中的坐标;△X0，△Y0，△Z0表示坐标转换的平移参数;ωX，ωY，ωZ表示坐标转换的旋转参数;m表示坐标转换的尺度比参数。

2.2 九参数法

考虑到实际情况中，坐标系的三个坐标轴的缩放因子不可能完全一致，因此考虑采用九参数法解决空间直角坐标基准的转换问题，其模型为:

式中:mX，mY，mZ表示坐标转换的尺度比参数。

2.3 空间直角坐标与大地坐标的互换

不考虑大地高H时，空间直角坐标与大地坐标的互换由下式给出［2］:

其中X，Y，Z为椭球上点位在空间直角坐标系中的坐标，L，B为相应的大地经、纬度，H为转换点在椭球的大地高(高程异常可在高程异常图中近似内插求得)。e为椭球第一偏心率，N为卯酉圈曲率半径，且

3 数据实验与比较分析

某市C级GPS控制网65个点组成，其中有30个点为原国家一等三角点，采用10个具有“北京54坐标系”和“西安80坐标系 ”的重合点，具体点位分布情况如图2所示。

图2 被采用的重合点点位分布图

从测绘局资料处获得该10个点分别在北京54坐标系下和西安80坐标系下的平面坐标，据高斯投影反算得到大地坐标，高斯反算公式［1］:

式中凡脚注有“f”的函数符号都是以垂足纬度Bf代入求得的。而垂足纬度Bf可以根据子午线弧长公式，由x=X很快求出。这样根据式(6)就可以计算大地纬度B和经差l，进而求得大地经度L，具体解法参见［3］。

利用式(3)即可得到北京54坐标系下的空间直角坐标(X54，Y54，Z54)。然后利用3个公共点的坐标计算出坐标转换的七参数和九参数，利用七参数法和九参数法分别得到两组在西安80坐标系下的新的空间直角坐标()和()，根据高斯反算式(6)分别求得两组西安80坐标系下的大地坐标，再代入式(4)即可求出两组新的西安坐标系下的平面坐标)，最后将经转换得到西安80坐标系数据成果同该坐标系检核数据成果进行比较分析。具体研究技术路线如图3所示。

图3 研究技术路线示意图

通过计算可知利用七参数法和九参数法所得的新坐标与已知坐标在X轴，Y轴，Z轴方向均有一定的较差，部分点较差如表3所示。

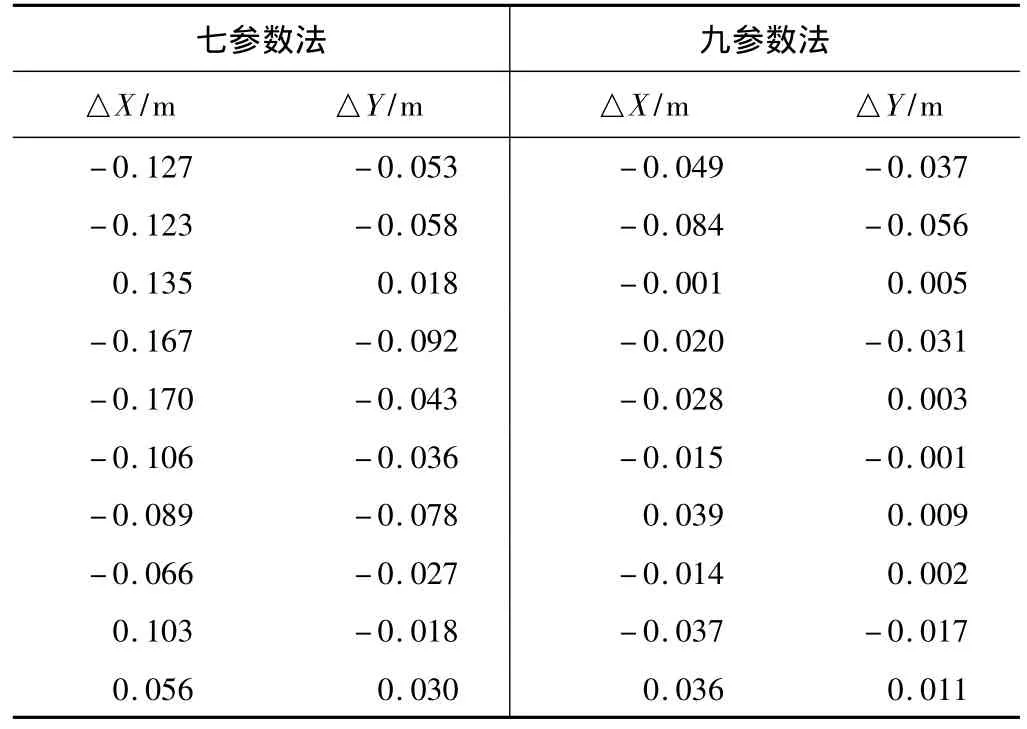
误差统计分析 表2

式中，Xi真值，Yi真值均为已知坐标;Xi计算值，Yi计算值均为利用坐标转换参数转换的坐标;△Xi，△Yi，均为已知坐标与转换坐标之差;mX为X坐标转换中误差，mY为Y坐标转换中误差。

图4 X分量较差

图5 Y分量较差

由于计算精度的限制，虽利用九参数法进行坐标转换得到的个别点的新坐标与原坐标的差值比七参数法得到的大，但从表2和图4、5中可以直观地看到九参数法整体优于七参数法。具体分析结果如下:

七参数法精度分析 表3

九参数法精度分析 表4

5 结论

本文通过对上述实验数据的分析和比较，可知，利用九参数法得到的平面坐标与已知坐标在各个坐标轴方向上的最大差值、最小差值以及中误差均小于七参数法得到的。由此得到结论:利用九参数法解决空间直角坐标基准转换问题在实际应用中具有一定的可行性，同时其精度要比七参数法高。

［1］孔祥元，郭际明，刘宗泉.大地测量学基础［M］.武汉:武汉大学出版社，2005.

［2］刘大杰.全球定位系统的原理与数据处理［M］.上海:同济大学出版社，1996.

［3］王彦伟，李海洋，裴亮等.高斯反算三种实用算法的比较研究［J］.矿山测量，2008(1):48－50.

［4］武汉测绘科技大学测量平差教研室.测量平差基础(第三版)［M］.北京:测绘出版社，2007.

［5］杨元喜.2000中国大地坐标系［J］.科学通报，2009，54(16):2271－2276.

［6］杨元喜.中国大地坐标系建设主要进展［J］.测绘通报，2005，52:6 －9.

［7］顾旦生，张莉，程鹏飞等.我国大地坐标系发展目标［J］.测绘通报，2003，3:1 －4.

［8］王解先.七参数转换中参数之间的相关性［J］.大地测量与地球动力学，2007，27(2):43 －46.

［9］王解先，徐志京.三种坐标间转换的雅可比矩阵数值导数计算方法［J］.大地测量与地球动力学，2004，24(4):19－23.

［10］王解先，王军，陆彩萍.WGS84与北京54坐标的转换问题［J］.大地测量与地球动力学，2003，23(3):70－73.

［11］王解先，邱杨媛.高程误差对七参数转换的影响［J］.大地测量与地球动力学，2007，27(3):25－27.

［12］徐仕琪，张晓帆，周可法等.关于利用七参数法进行WGS－84和BJ－54坐标转换问题的探讨［J］.测绘与地理空间信息，2007，30(5):33 －42.

［13］茹树青，吉长东，王宏宇.RTK坐标转换中四参数法与七参数法精度比较［J］.东北水利水电，2006，24(262):67－68.

［14］丛枝鲜，朱金海，李秀海.GPS坐标成果的游动九参数转换法［J］.交通科技与经济，2009，3(11):104－106.

［15］柳光魁，赵永强，张守忱等.北京54和西安80坐标系转换方法及精度分析—基于大连市C级GPS网成果［J］.测绘与空间地理息，2007，30(2):138 －142.

［16］武继军.不同大地坐标系间坐标转换模型研究［J］.河南理工大学学报，2006，25(5):282－285.