泡沫铝三明治板冲压成形数值模拟分析

陈盛贵 罗剑英 邓世春 孙振忠

(东莞理工学院 机械工程学院，广东东莞 523808)

泡沫铝是一种以纯铝或铝合金为基质，存在着大量连通的或闭合的孔洞结构的新型多功能材料，具有质轻、吸声、隔热、阻燃、电磁屏蔽、吸收冲击能等优异性能［1］。泡沫金属作为结构件通常都与传统的致密金属组合成复合构件使用，实现最佳的力学性能［2］。高技术的需求使得具有更高比强度、比刚度的泡沫铝夹芯结构正成为研究热点之一［3］。泡沫铝夹芯结构可分为两种:夹芯板结构、填充管结构。夹芯板结构通常是芯层为泡沫铝，上下层为铝板或其他金属薄板，例如泡沫铝三明治 (Aluminum Foam Sandwich，AFS)板材。

国外对泡沫铝夹芯结构的应用及力学性能已经开展了较为深入的研究。工程上已通过冲压工艺成形AFS板材轻型结构件。AFS板材冲压结构件相对于传统的钢制结构件，受载时有更均匀且更低的等效应力分布，对车身抗冲击安全性有较大的提高［4］。Contorno D等［5］研究了AFS板材的冲压性能，试验和数值模拟相结合研究了成形过程中板厚的变化规律，以及泡沫芯材料相对密度的变化及分布，试验和数值计算结果符合的较好。

与国外相比，国内对泡沫铝夹芯结构的应用及力学性能的研究较少，起步较晚。谢中友等［6］用实验和数值模拟的方法研究了泡沫铝填充薄壁圆管的三点弯曲行为，结果表明填充泡沫铝后，薄壁圆管三点弯曲承载能力有很大的提高。许坤等［7］通过理论进一步研究了泡沫铝填充薄壁方管的弯曲行为，在实验基础上提出了一个分析填充结构弯曲行为的理论方法。孙振忠等［8－10］通过实验方法研究了AFS板材弯曲成形工艺，分析了AFS板材冲压成形宏微观协调变形机制以及AFS板材冲压成形板面－泡沫铝芯间界面剥离、圆角处过度减薄、泡沫铝芯剪应力裂纹等主要成形缺陷，探讨了AFS板材压边力和冲压成形板厚的控制规律，最终通过变压边力工艺控制、强化芯材－面板结合强度等方法，显著提高了AFS板材的成形极限和成形质量。

上述的研究成果主要关注泡沫铝夹层结构的力学性能、承载能力、结构模型及数值模拟，对AFS板材冲压成形宏微观变形涉及到的问题研究较少。三明治板材板面与泡沫铝芯间大变形时界面特性和力学过程的交互影响，以及板面金属和泡沫铝之间大变形时不同的屈服特征，给三明治板材冲压成形的研究带来困难。

本文运用塑性力学理论研究泡沫金属材料有限元模型，并利用ABAQUS软件对AFS板材弯曲成形过程进行有限元数值模拟，结合文献［8－10］中的实验结果，最终分析AFS板材的冲压成形缺陷，为AFS板材冲压成形研究提供有效的数值模拟方法。

1 有限元模型基础理论

泡沫金属材料的力学性能依赖于孔壁材料的性质、材料的相对密度和孔的拓扑结构 (如孔的开、闭性，孔的形状和尺寸)等［11－12］。此外，泡沫金属材料的缺陷 (如孔的弯曲与破损)和裂纹对其力学性能也产生很大影响［13］。这些都表明泡沫金属材料的力学性能与一般金属材料相比有较大的不同。孔隙的存在使泡沫材料的性质不同于普通致密材料。孔隙的效应反映在塑性变形性能上，使材料呈现塑性可压缩性，这一点与普通 (或经典)的塑性不同。由于出现了塑性可压缩性，平均应力σm=σkk/3或静水压力p=－σkk/3必然要进入屈服判据和本构方程式，实验观测和理论模拟的重点也集中在这一点上。

随着泡沫金属材料在工程领域中的广泛应用，许多学者对其力学性能进行了深入的研究。其中Deshpande和Fleck对泡沫金属材料连续本构模型进行了较系统的研究［14］，Deshpande和Fleck的模型简称DF模型。DF模型考虑了平均应力σm或静水应力p在塑性本构关系中的重要作用，引进塑性泊松比vp作为新的材料参量，这些参量被作为塑性可压缩性的一个定量描述。对于各向同性强化的DF模型，可以把屈服面/加载面方程写成下面的一般形式:

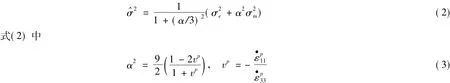
α为屈服面形状参数，刻画泡沫材料的塑性可压缩性，vp即所谓塑性泊松比，σe为von Mises有效应力，即

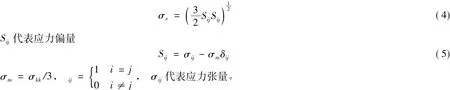
当α=0时，则DF广义有效应力还原为von Mises有效应力。但对泡沫金属材料而言，α≠0，一般地0＜ α2≤ 4.5。

在式(1)中，若

则式(1)代表初始屈服面。若

式(7)中h代表一个刻画材料变形历史的参量，则式(1)为屈服面演化方程，或加载面方程。

对于自相似各向同性硬化材料，根据流理论可以得到

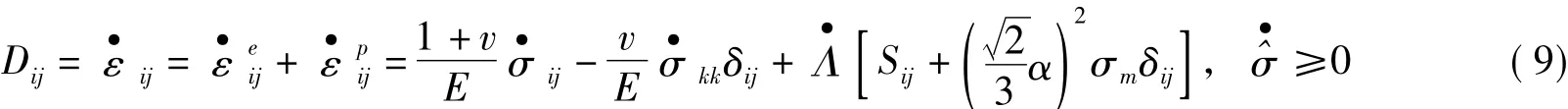
式(9)中

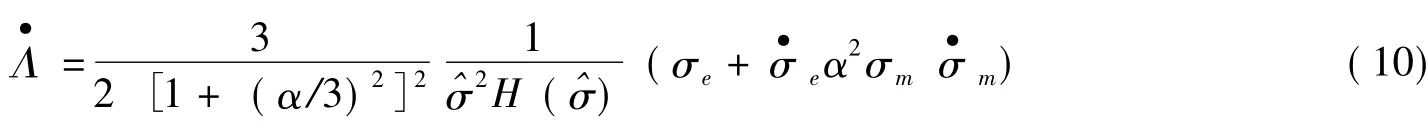
称为广义塑性流动因子。

DF模型形式简洁，使复杂的泡沫材料变形与强度 (包括断裂)问题的定量分析成为可能，甚至使解析求解成为可能，大大方便了分析研究，被广泛用来研究泡沫材料的各种力学行为。

2 弯曲成形数值模拟

2.1 有限元模型

建立泡沫铝材料的本构关系是AFS板材弯曲成形数值模拟研究的基础。本文应用有限元分析软件ABAQUS 6.11中专门用于金属成形分析的Explicit显式模块对AFS板材弯曲成形工艺过程进行数值模拟。弯曲成形数值模拟主要是研究AFS板材在凸模作用下的塑性变形行为和变形破坏规律。弯曲成形模具结构及尺寸如图1、图2所示，凹模中间槽位尺寸为40 mm×86 mm，圆角半径为10 mm;凸模为圆角半径为5 mm的平底冲头。

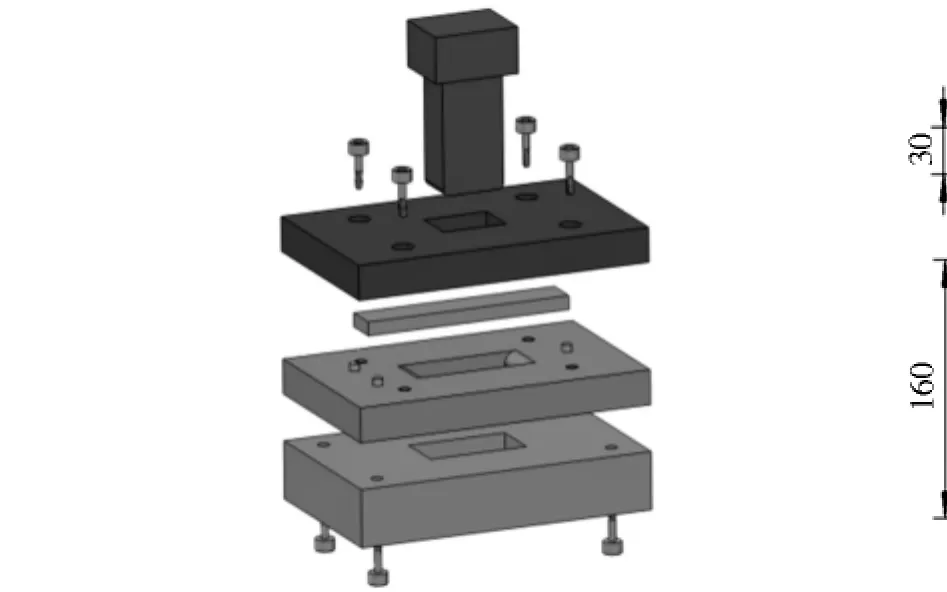
图1 实验模具结构

图2 凹模及凸模尺寸

数值模拟中，针对泡沫铝材料采用目前应用较广泛的各向同性强化本构模型［14］，即DF模型，并使用ABAQUS材料库中提供的可压缩泡沫材料模型;针对金属面板材料采用弹塑性本构模型 (Mises屈服面)，且不考虑各向异性的影响。有限元模型及网格划分如图3、图4所示。有限元模型的建立统一采用SI单位，凸模、凹模及压边装置简化为刚体材料，采用四节点刚体壳单元进行网格划分;凹模的六个刚体自由度全部被约束，凸模和压边装置被约束五个刚体自由度，保留竖直方向的平移自由度。上、下面板与芯材采用八节点六面体线性减缩积分单元建模，并进行沙漏控制，使用C3D8R单元进行网格划分。

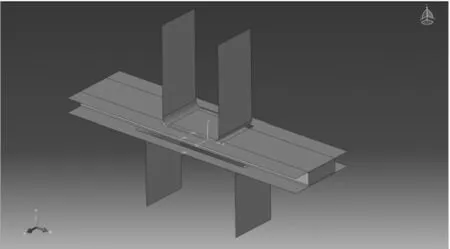
图3 有限元模型

图4 网格划分

2.2 材料模型及相关参数

上、下面板材料采用HRB335级钢材，材料密度为ρ=7800 Kg/m3、弹性模量为E=200 Gpa、弹性泊松比为v=0.3。泡沫铝采用Al－Mg－Si合金粉末为主要材料，材料密度为ρ=270 Kg/m3、弹性模量为E=4 Gpa、初始屈服强度为σ1=5 Mpa、硬化模量为Ep=1 Mpa、弹性泊松比为ve=0、塑性泊松比为vp=0、屈服面形状参数为α≈2.12(对于一般金属材料，由于其塑性体积的完全不可压缩性，塑性泊松比vp=0.5;而对于完全可压缩的泡沫金属材料，塑性泊松比vP=0，由式 (3)可知，α≈2.12)。

2.3 边界条件及载荷

凸模以200 mm/s的速度匀速下压，下压总位移约为40.33 mm;压边装置采用文献［9］中优化后的变压边力工艺曲线进行控制。在有限元分析过程中假定上、下面板与泡沫铝粘接很好，不发生分层破坏。该有限元模型中包括有三对接触，分别是凸模和AFS板材上板面的面面接触，以及压边装置、凹模和AFS板材上、下板面的面面接触。在三对接触中，作为刚体材料的凸模、凹模和压边装置设置为接触主面，而较软的AFS板材上、下板面为接触从面。为保证计算的收敛性和减少接触时的侵透量，从面的网格尺寸应小于主面的网格尺寸。ABAQUS的Explicit显式模块提供了罚函数方法和动态约束方法两种接触计算方法。本模型采用罚函数法计算接触，它具有对称性，动量守恒准确，不需要碰撞和释放条件，很少引起沙漏效应，噪声小，在数值计算中被广泛使用。

3 数值模拟结果

AFS板材弯曲成形的数值模拟分析结果如下。

在成形深度h=2.25 mm时，泡沫铝部分的Von Mises应力和平均压力云图如图5、图6所示，在与凸模圆角接触的领域产生了明显的应力，并且满足了屈服条件，进入了塑性变形状态;而AFS板材其它区域仍然处于弹性变形状态。

图5 成形深度h=2.25 mm时泡沫铝部分的Von Mises应力

图6 成形深度h=2.25 mm时泡沫铝部分的平均压力p

在成形深度h=24.19 mm时，泡沫铝部分的Von Mises应力在中性轴上、下方区域基本对称;而平均压力的计算云图同样显示 (如图7、图8所示)，中性轴上方靠近凸模的单元处于受压状态，而下方的单元则处于受拉状态。

图7 成形深度h=24.19 mm时泡沫铝部分的Von Mises应力

图8 成形深度h=24.19 mm时泡沫铝部分的平均压力p

在成形深度h=38.1 mm时，泡沫铝部分底部单元的等效塑性应变达到设定的极限值，单元产生破坏，这时板材的承载力开始下降，图9、图10、图11中显示泡沫铝部分开始破坏的情形。随后裂纹沿着泡沫铝的中央从底向上持续发展，直到成形深度h=40.33 mm时，泡沫铝部分被压断，这时承载力下降为0。凸模接触反力和成形深度的关系曲线如图12所示。

图9 成形深度h=38.1mm面时泡沫铝部分的Von Mises应力

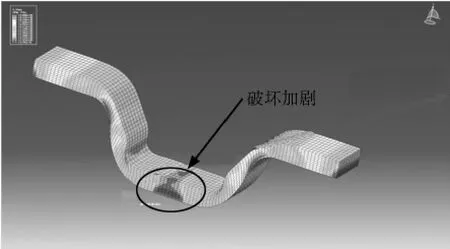
图10 成形深度h=40.01mm时泡沫铝部分的Von Mises应力

图11 成形深度h=40.33mm时泡沫铝部分的Von Mises应力

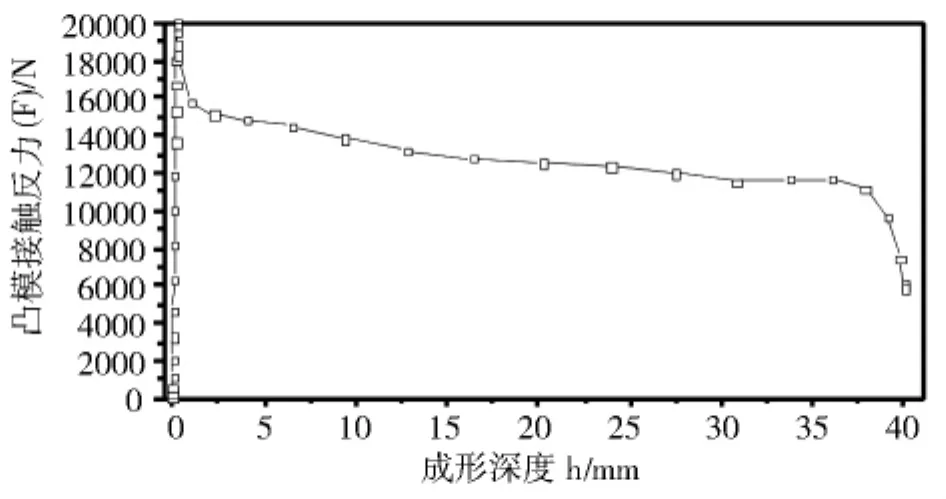
图12 凸模接触反力与成形深度的关系

4 讨论和分析

4.1 泡孔塑变微观组织结构演化

三明治板材压缩成形区域的压缩变形可分为弹性变形、坍塌、密实等3个阶段。弹性变形可以恢复，当作用于孔壁的力矩超过纯塑性力矩时，就开始塑性坍塌，并产生塑性变形。密实阶段试样孔楞或孔壁基本上全被压垮，挤压到一起，继续压缩时材料本身也要变形 (如图13所示)。

4.2 界面剥离

成形深度继续增大时，泡沫铝与板面结合处出现了较大的应力分布，如图14中数值模拟结果所示。由于冲压深度较大，面板弯曲，在实验过程中面板与泡沫芯间会出现明显的分离现象，这种界面分离主要是由于板面与泡沫铝芯间剪切应变产生的。

图13 圆角处泡沫铝密度变化云图

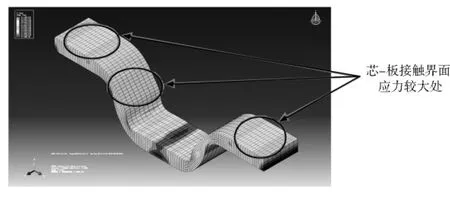
图14 泡沫铝与板面接触界面的应力云图

4.3 剪应力裂纹

在凸模的作用下，板料侧壁悬空部分，上面板受凸模向中心的拉力作用，下面板受凹模摩擦形成向外的拉力作用。在板厚方向上形成不同轴力的平衡，产生板材厚向应力和应变梯度效应诱发不均匀弯矩，使板芯区域形成很大的剪应力区，如图15所示。

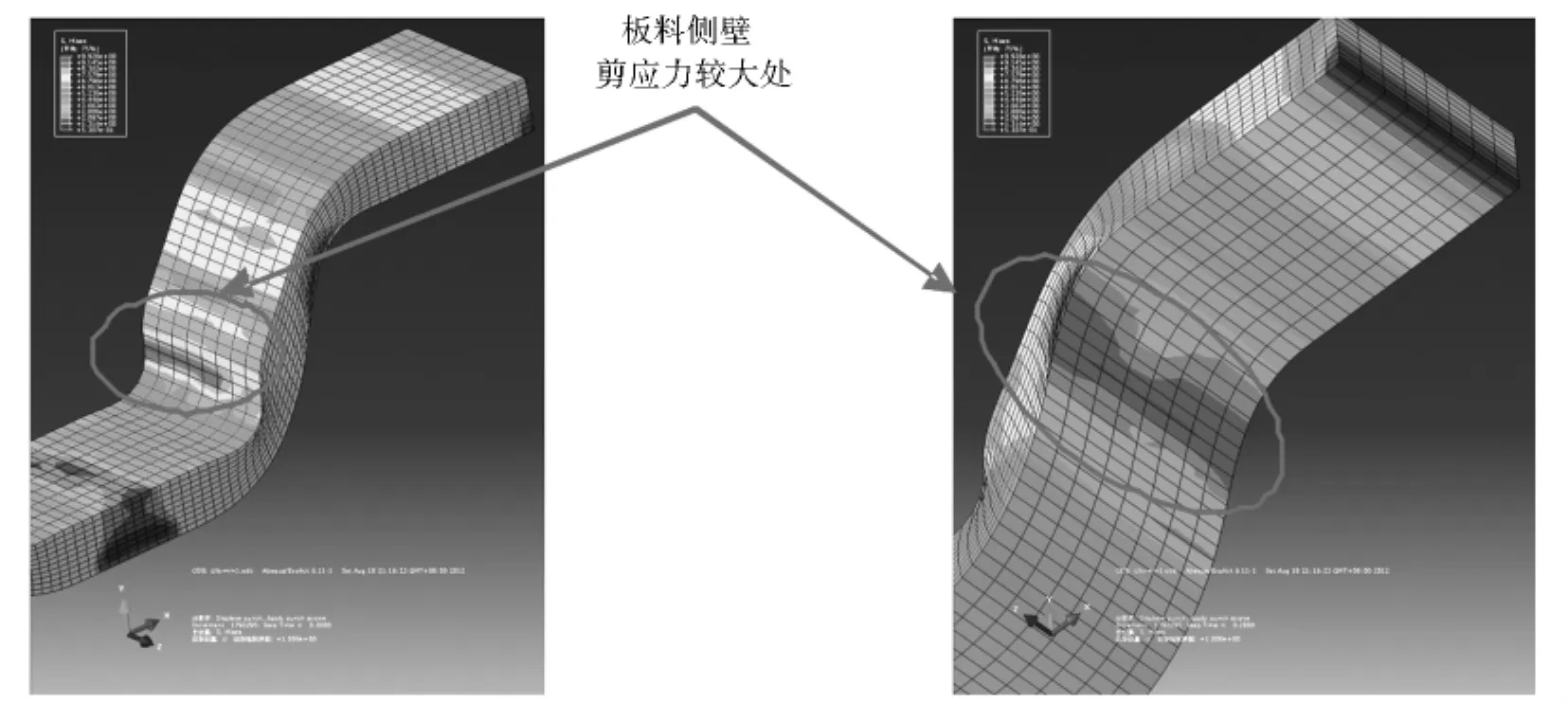
图15 板料侧壁剪应力分布云图

4.4 过渡圆角处板厚减薄

较小的圆角半径会使内表面承受较大压缩应力，外表面承受较大的拉伸应力，且变形不均匀，弯曲件过渡圆角处板厚减薄如图16所示。

图16 数值模拟件过渡圆角板厚减薄

5 结语

本文运用塑性力学理论研究泡沫金属材料的有限元模型，并利用ABAQUS软件对AFS板材弯曲成形过程进行有限元数值模拟。结合文献［8－10］中的实验结果，最终分析AFS板材的冲压成形缺陷，研究结论如下:

1)数值模拟结果与文献中的实验结果符合的较好，为AFS板材冲压成形研究提供有效的数值模拟方法。

2)在变形的初始阶段，泡沫铝部分经历了很短的弹性变形阶段，之后进入一个较长的屈服平台段。当成形深度为38.1 mm时，泡沫铝部分开始破坏，承载力下降，直到成形深度为40.33 mm时，试件完全丧失承载力。由于ABAQUS软件中的可压缩泡沫材料模型不能添加破坏参数，所以无法模拟破坏之后的情形，因此在达到破坏极限时，计算出来的承载力仍比较大，无法一下子完全丧失承载力，下降为0。

3)通过AFS板材的数值模拟分析可知，AFS板材冲压成形主要缺陷为界面剥离、剪应力裂纹、过渡圆角处板厚减薄等;采用文献中的变压边力控制方法进行数值模拟，有效地抑制了成形缺陷，使AFS板材在合理的受力、变形和流动状态下成形，显著提高了成形极限。

［1］黄安斌，胡治流，温石坤.泡沫铝材料结构与性能及其应用研究［J］.金属功能材料，2010，17(4):62－65.

［2］张敏，祖国胤，姚广春，等.泡沫铝夹心板的制备及其界面结合机理的研究［J］.功能材料，2006，37(2):281－283.

［3］梁晓军，朱勇刚，陈锋，等.泡沫铝芯三明治板的粉末冶金制备及其板/芯界面研究［J］.材料科学与工程学报，2005，23(1):77－80.

［4］Emmelmann H J，Bunsmann W，Seeliger W，et al.Complex shaped aluminium sandwich panel with aluminium foam［A］.International Conference on IBEC 97［C］.Stuttgart Germany，1997.

［5］Contorno D，Filice L，Fratini L，et al.Forming of aluminum foam sandwich panels:Numerical simulations and experimental tests［J］.Journal of Materials Processing Technology，2006，177(1－3):364－367.

［6］谢中友，李剑荣，虞吉林.泡沫铝填充薄壁圆管的三点弯曲实验的数值模拟［J］.固体力学学报，2007，28(3):261－265.

［7］许坤，寇东鹏，王二恒，等.泡沫铝填充薄壁方形铝管的静态弯曲崩毁行为［J］.固体力学学报，2005，26(3):261－266.

［8］孙振忠，何伟锋，陈盛贵.泡沫铝三明治板材弯曲成形试验研究［J］.精密成形工程，，2010，2(2):61－64.

［9］孙振忠，陈海彬.泡沫铝三明治板材U型弯曲成形变压边力控制研究［J］.锻压技术，2010，35(4):44－48.

［10］孙振忠，陈盛贵，陈海彬，等.泡沫铝三明治板材冲压界面剥离性能研究［J］.材料科学与工艺，2010，18:39－43.

［11］Lorna J Gibson，Michael F Ashby.Cellular Solids:Structure and Properties［M］.Cambridge:Cambridge University Press，1997.

［12］Ashby M F，Evans G A，Fleck N A，et al..Hutchinson and H.N.G.Wadley.Metal Foams:A Design Guide［M］.Oxford:Butterworth Heinemann，2000.

［13］Fleck N A，Olurin O B，Chen C，et al.The effect of hole size upon the strength of metallic and polymeric foams［J］.Journal of the Mechanics and Physics of Solids，2001，49(9):2015－2030.

［14］Deshpande V S，Fleck N A.Isotropic constitutive models for metallic foams［J］.Journal of Mechanical Physical Solids，2000，48(6 －7):1253－1283.

［15］RuiPing Guo，YW Mai，TianYou Fan，et al..Plane stress crack growing steadily in metal foams［J］.Materials Science and Engineering A，2004，381(1－2):292－298.