重力坝深层抗滑稳定分析中扬压力施加方法

黄耀英，沈振中，郑 宏

（1.三峡大学水利与环境学院，湖北宜昌 443002；2.河海大学水利水电学院，南京 210024；3.中国科学院a.武汉岩土力学研究所；b.岩土力学与工程国家重点实验室，武汉 430071）

重力坝深层抗滑稳定分析中扬压力施加方法

黄耀英1，沈振中2，郑 宏3a，3b

（1.三峡大学水利与环境学院，湖北宜昌 443002；2.河海大学水利水电学院，南京 210024；3.中国科学院a.武汉岩土力学研究所；b.岩土力学与工程国家重点实验室，武汉 430071）

针对采用有限单元法对扬压力进行计算时，常容易发生疑惑而导致错误的问题，首先对比分析了双斜面深层抗滑稳定分析时2种不同扬压力的作用方式，然后研究了采用有限元法分析重力坝沿坝基面或深层双斜面抗滑稳定时扬压力的施加方式。分析认为：扬压力作为面荷载作用在滑面上，或作为体荷载作用在滑块上，虽然总的作用力近似相等，但由于滑块为变形体，不一定引起相近的效应量（位移和应力等）；其中，在垂直方向分别按面荷载或体荷载作用引起的差异，相对于在水平方向分别按面荷载或体荷载作用引起的差异来说，前者引起的差异较后者引起的差异大一些。

扬压力；重力坝；有限元法；坝基面；双斜面

1 研究背景

在混凝土坝工程中，扬压力是一种重要而特殊的荷载。混凝土重力坝设计规范（SL319—2005，DL5108—1999）规定，坝体抗滑稳定分析采用刚体极限平衡法进行分析，并采用有限元法作为辅助方法。当采用刚体极限平衡法进行沿坝基面抗滑稳定分析时，在坝基面施加扬压力（面力）；对于深层抗滑稳定分析时，在滑面上施加扬压力（面力）。当采用有限单元法对扬压力进行计算时，常容易发生疑惑而导致错误。虽然目前许多学者对重力坝坝基扬压力进行了研究［1－2］，但仍存在较大的分歧。赵代深［3］指出采用有限元法分析混凝土坝时，在坝面、库底施加静水压力和沿坝底面施加扬压力（面荷载）的方法是不可取的，认为这种扬压力施加方法忽略了坝体内的扬压力。林绍忠［4］提出在坝基面单元两侧同时作用一对大小相等、方向相反的渗透压力（面荷载），这种施加方式只是对坝基面薄层单元的应力产生影响，忽略了渗透压力对坝体、基岩内部应力的影响。段亚辉等［5］在分析重力坝碾压层面失稳时，按规范给定的图形在计算层面施加扬压力，计算出的坝体竖向位移和应力与所考虑的层面位置有关。王媛等［6］对作用在坝基的水荷载组合方式进行了研究。柴军瑞［7］对作用在混凝土坝上的水荷载进行了讨论。张有天［8］认为混凝土坝虽然透水，但因坝体渗透系数很小，水力梯度很大，可近似按不透水介质处理，此时其上游面作用水压力（面荷载），建基面作用扬压力（面荷载）。范书立等［9］对渗透压力对重力坝有限元分析的影响进行了研究，建议将规范规定的扬压力分布线沿坝基面向上对折，作为坝体简化的浸润线，浸润线以下坝体采用浮重度的方式考虑坝基扬压力，即建议将扬压力作为体积力（浮力）考虑。梁通等［10］所持“扬压力一般分为浮托力和渗透压力2部分，扬压力等于作用面上孔隙水压力之和”的观点是扬压力的裂缝理论，而按照孔隙理论，扬压力是一种体积力，实质上就是静水浮力，其大小与渗透压力无关。显然，扬压力如何考虑，对混凝土坝工程的应力和位移的合理计算存在较大影响。另外，进行重力坝深层抗滑稳定分析时，作用在滑面上的扬压力，不同的专家也存在一些分歧。针对这些问题，本文首先对比分析双斜面深层抗滑稳定分析时2种不同滑面上扬压力的作用方式，接着探讨采用有限元法分析沿坝基面和深层抗滑稳定时扬压力的施加方式。

2 双斜面深层抗滑稳定分析时2种不同扬压力作用方式对比分析

设某重力坝坝基和坝体都没有进行防渗排水措施，在坝基存在AB和BC两条软弱面，上游水深H，下游无水，目前有如下2种滑面扬压力的施加方式，如图1所示。

图1 双斜面深层抗滑稳定分析时扬压力作用图Fig.1 Sketch of up lift pressure acting on double inclined p lanes in deep sliding stability analysis

将图1（a）双斜面上的扬压力分解为垂直向合力和水平向合力，有

区域ABD垂直向合力0.5ρgyLAD＋0.5ρgHLAD（↑），区域ABD水平向合力0.5ρgy2＋0.5ρgHLy（→）；

区域BCD垂直向合力0.5ρgyLCD（↑），区域BCD水平向合力0.5ρgy2（←）。

将图1（b）双斜面上的扬压力分解为垂直向合力和水平向合力，有

区域ABD垂直向合力0.5ρgyLAD＋ρgHLAD（↑），区域ABD水平向合力0.5ρgy2＋ρgHy（→）；

区域BCD垂直向合力0.5ρgyLCD＋0.5ρgHLCD（↑），区域BCD水平向合力0.5ρgy2＋0.5ρgHy（←）。

分析可知：

（1）图1（a）区域ABD垂直向合力第一项为区域ABD受到浮力的合力，第二项为坝基面AD受到三角形分布的扬压力的合力；图1（a）区域BCD垂直向合力为区域BCD受到浮力的合力；图1（a）区域ABD和区域BCD总的水平向合力为0.5ρgHy（→）。即图1（a）中斜面AB和BC上扬压力的合力，在垂直向等价于区域ABCDA受到浮力的合力（0.5ρgyLAD＋0.5ρgyLCD），以及坝基面AD受到三角形分布扬压力的合力（0.5ρgHLAD）；在水平向合力为0.5ρgHy。

（2）图1（b）区域ABD垂直向合力第一项为区域ABD受到浮力的合力，图1（b）区域BCD垂直向合力第一项为区域BCD受到浮力的合力；除此之外，在区域ABD上还受到垂直向合力ρgHLAD，区域BCD上还受到垂直向合力0.5ρgHLCD；图1（b）区域ABD和区域BCD上受到水平向总的合力为0.5ρgHy（→）。即图1（b）中斜面AB和BC上扬压力的合力，在垂直向等价于区域ABCDA受到浮力的合力（0.5ρgyLAD＋ 0.5ρgyLCD），以及ρgHLAD＋0.5ρgHLCD；在水平向为0.5ρgHy。

（3）图1（a）和图1（b）滑块上水平向总的合力相等，但图1（b）垂直向合力大于图1（a）。由于实际工程的岩基十分复杂，导致实际的裂隙渗流十分复杂，当且仅当软弱面AB完全贯通，不存在任何阻水效应，以致和库水形成“连通器”，而软弱面BC没有贯通，此时，可采用图1（b）的扬压力作用方式。一般情况下，软弱面AB和BC均没有完全贯通，存在阻水效应，此时，宜采用图1（a）的扬压力作用方式。

3 有限元法分析重力坝抗滑稳定时扬压力的施加方式

3.1 有限元分析坝基面抗滑稳定时扬压力的施加方式

设某重力坝坝基和坝体都没有进行防渗排水措施，上游水深90 m，下游无水，底宽70 m，如图2。采用有限元法进行该重力坝沿坝基面抗滑稳定分析，对比分析了4组不同扬压力施加方式。虽然刚体极限平衡法仅考虑滑裂面上的合力，而忽略力矩的作用效应，但采用刚体极限平衡法进行沿坝基面抗滑稳定分析得到工程界广泛认可，为此，将有限元法计算结果与刚体极限平衡法计算结果进行对比。为对比分析更加直观，以下着重分析采用不同扬压力施加方式进行有限元分析时，在坝基面上的垂直向合力，并与刚体极限平衡法分析时的坝基面合力进行对比。4组不同扬压力施加方式工况如下。

工况11：大坝有限元模型采用粗网格模型，混凝土弹性模量20 GPa、泊松比0.2，岩基变形模量18 GPa、泊松比0.25，扬压力作为面荷载作用在坝基面。

工况12：有限元模型同工况11，参考范书立等［9］研究，扬压力分布线沿建基面向上对折，作为坝体简化的浸润线，浸润线以下的坝体作用浮力（体积力）。

工况21：在工况11的有限元模型基础上，在坝基面处增设一厚度0.1 m的夹层单元，为保证夹层单元的计算精度，尽量使夹层单元的棱边夹角接近90°，以获得良好的夹层单元形态，夹层单元弹性模量和坝体混凝土相同，扬压力作为面荷载作用在夹层单元底面。

工况22：有限元模型同工况21，扬压力施加方式同工况12。

工况3：有限元模型同工况21，扬压力作为面荷载作用在夹层单元顶面。

工况4：在工况11的有限元模型基础上，在坝基面处增设厚度为0.05 m的2层夹层单元，夹层单元尽量保证良好的单元形态，扬压力作为面荷载作用在2层夹层单元最顶面。

采用有限单元法对上述4组工况进行分析，取出坝基面附近的垂直向节点应力和高斯点应力，然后积分获得坝基面垂直向合力见表1。采用刚体极限平衡法直接计算时，坝基面扬压力合力为3.087 0× 107N（记为扬压力标准值）。

表1 扬压力不同施加方式下坝基面附近节点和高斯点垂直向合力Table 1 Vertical resultant forces at dam foundation’s nodal and Gaussian points w ith differentmethods of applying uplift pressure

由分析可见：

（1）扬压力分布线沿建基面向上对折，作为坝体简化的浸润线，浸润线以下的坝体采用浮重度的方式考虑扬压力，即使大坝有限元模型的网格较粗，也可以获得精度良好的计算结果。但对于较粗的有限元网格，由于单元较大，应力存在一定的均化效应，对计算精度有一定的影响。而在坝基面处设置一夹层单元，可以克服应力均化效应，计算精度更高。如在坝基面处设置一夹层单元，工况22计算的节点垂直向合力和高斯点垂直向合力分别为3.021 6×107N和3.088 3×107N，与扬压力标准值3.087 0×107N十分接近。

（2）扬压力作为面荷载作用在坝基面，如果大坝有限元网格较粗，此时计算的节点垂直向合力和高斯点垂直向合力，都与扬压力标准值相差很大。当在坝基面附近设置一层夹层单元时，而扬压力作为面荷载作用在夹层单元顶面时，夹层底面节点垂直向合力和高斯点垂直向合力，与扬压力标准值较为接近，其中高斯点垂直向合力十分接近扬压力标准值。为了克服应力均化效应，在坝基面附近设置2层夹层单元，同时扬压力作为面荷载作用在2层夹层单元最顶面时，此时，夹层中面的节点垂直向合力也十分接近扬压力标准值。

（3）本文对比分析了夹层单元弹性模量取小值，其分析结果与夹层单元弹性模量取坝体混凝土弹性模量时的计算规律基本一致。

（4）由上述分析可见，采用有限元法进行沿坝基面抗滑稳定分析时，当在坝基面设置夹层单元，同时在坝基附近的混凝土和岩体均采用细网格时，此时，采用扬压力分布线沿建基面向上对折，作为坝体简化的浸润线，浸润线以下的坝体采用浮重度的方式考虑扬压力，以及扬压力作为面荷载作用在夹层单元顶面，2种不同的扬压力作用方式，引起的坝基面节点垂直向合力和高斯点垂直向合力，与扬压力标准值接近。但2种不同的扬压力作用方式并不一定引起大坝其余部位相近的位移和应力。

3.2 有限元分析双斜面深层抗滑稳定时扬压力的

施加方式

设某重力坝坝基和坝体都没有进行防渗排水措施，上游水深90 m，下游无水，底宽70 m，岩基内存在双斜面AB和BC，BD的深度为20 m，DC的宽度为50 m，如图3。采用有限元法进行该重力坝双斜面深层抗滑稳定分析，对比分析了3组不同扬压力施加方式。与3.1节类似，双斜面深层抗滑稳定分析时，将有限元计算结果与刚体极限平衡法计算结果进行对比。为对比分析更加直观，有限元法分析采用不同扬压力施加方式时，在滑块上的法向合力和切向合力，并与刚体极限平衡法分析时双斜面上的合力对比。3组不同扬压力施加方式工况如下。

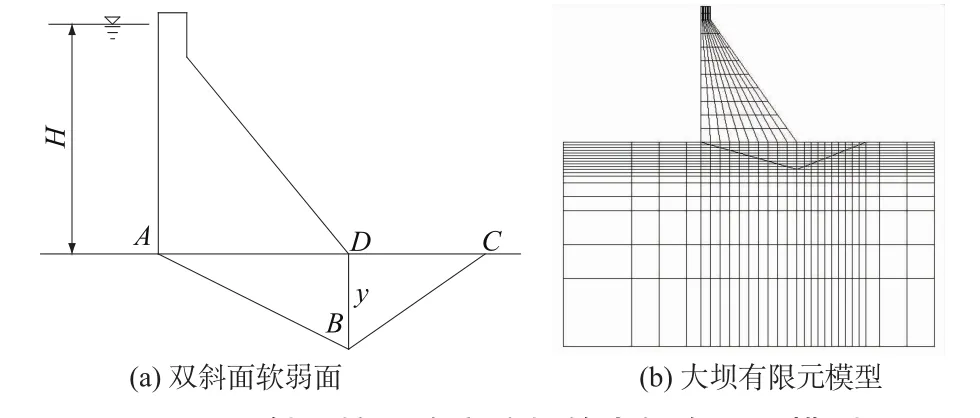
图3 双斜面抗滑稳定分析的大坝有限元模型Fig.3 Finite element dam model for the sliding stabilityanalysis for double inclined p lanes

工况1：大坝有限元网格如图3（b），混凝土弹性模量20 GPa，泊松比0.2，岩基变形模量18 GPa，泊松比0.25，双斜面采用厚度为0.1 m的夹层单元，夹层单元尽量保证良好的单元形态，双斜面夹层变形模量0.2 GPa，泊松比0.3，扬压力作为面荷载作用在双斜面的顶面（靠近滑块的面），作用方式如图1（a）；

工况2：大坝有限元网格如图3（b），假设坝体不透水，双斜面采用厚度为0.1 m的夹层单元，尽量保证良好的单元形态，夹层的渗透系数kj为岩基渗透系数kR的100倍，假设岩基为等效连续介质模型，先进行岩基稳定渗流场分析，获得岩基各节点水头H后，由节点水头计算获得渗流体积力，然后进行大坝和岩基的应力应变分析，此时，混凝土弹性模量20 GPa，泊松比0.2，岩基变形模量18 GPa，泊松比0.25，双斜面夹层变形模量0.2 GPa，泊松比0.3。参考本文第2节的垂直向和水平向受力特点，根据作用力施加方式的不同，又分为如下3种情况。

工况21a：岩基全区域作用工况2计算的水平向渗流体积力，且岩基全区域作用浮力；而坝基扬压力分布线沿建基面向上对折，作为坝体简化的浸润线，浸润线以下的坝体作用浮力。

工况21b：岩基全区域作用工况2计算的水平向渗流体积力，仅滑块ABCDA区域作用浮力；坝基扬压力分布线沿建基面向上对折，作为坝体简化的浸润线，浸润线以下的坝体作用浮力。

工况22：岩基区域仅滑块ABCDA区域作用工况2计算的水平向渗流体积力，而且岩基区域仅滑块ABCDA区域作用浮力；坝基扬压力分布线沿建基面向上对折，作为坝体简化的浸润线，浸润线以下的坝体作用浮力。

工况23：岩基区域仅滑块ABCDA区域作用浮力；参考图1（a）中，滑块ABCDA受到的水平向合力为0.5ρgHy，为此，假设在滑块ABCDA中面BD作用三角形分布的水平向面荷载，其中在D点的应力集度为ρgH，在B点的应力集度为0，水平向合力0.5 ρgHy；坝基扬压力分布线沿建基面向上对折，作为坝体简化的浸润线，浸润线以下的坝体作用浮力。

工况3：混凝土弹性模量20 GPa，泊松比0.2，岩基变形模量18 GPa，泊松比0.25，双斜面采用厚度为0.05 m的2层夹层单元，夹层单元尽量保证良好的单元形态，双斜面夹层变形模量0.2 GPa，泊松比0.3，扬压力作为面荷载作用在双斜面顶面（靠近滑块的面），作用方式如图1（a）。

当采用刚体极限平衡法对该重力坝双斜面进行抗滑稳定分析时，采用图1（a）计算的AB滑面的法向合力为3.924 0×107N，BC滑面法向合力为5.277 5×106N，记为扬压力标准值；当采用有限元法对上述3组工况进行分析，取出双斜面上的应力分量，转化获得双斜面法向和切向应力，然后积分获得双斜面法向和切向合力见表2，不同工况引起大坝典型部位位移见表3。表中，水平位移以向下游为正，垂直位移以上抬为正，反之为负；夹层顶面是指夹层靠滑块的面，夹层底面是指夹层远离滑块的面。其中，法向合力误差为有限元计算法向合力与刚体极限平衡法计算法向合力之差的绝对值与刚体极限平衡法计算法向合力的比值。

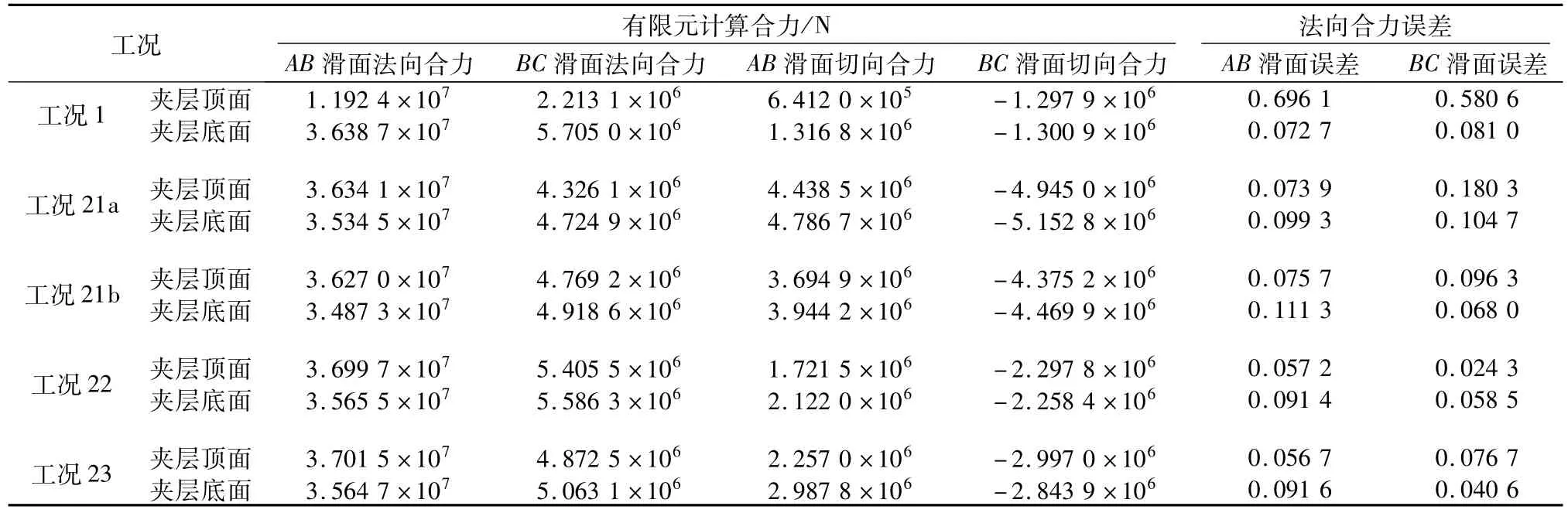
表2 不同工况下双斜面法向和切向合力Table 2 Normal and tangential resultant forces of double inclined planes in different cases

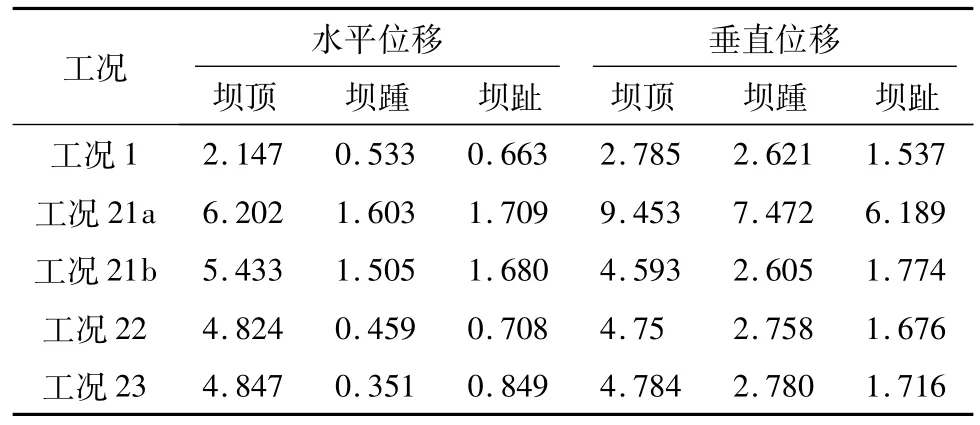
表3 不同工况下大坝典型部位位移Table 3 Disp lacements of typical parts of the dam in different cases mm

由分析可见：

（1）工况2计算的作用在滑块ABCDA区域水平向渗流体积力的合力为8.877 2×106N、垂直向渗流体积力合力为4.097×107N；按图1（a）计算的作用在滑块ABCDA区域水平向合力为8.820×106N、垂直向合力为4.263×107N，按图1（b）计算的作用在滑块ABCDA区域水平向合力为8.820×106N、垂直向合力为8.379×107N，由此可见，进行岩基稳定渗流场分析，然后由节点水头计算获得渗流体积力，其计算的结果更接近于图1（a）的计算结果。

（2）扬压力作为面荷载作用在滑块夹层顶面（工况1）时，进行有限元分析获得的夹层底面的法向合力和扬压力标准值（AB滑面3.924 0×107N，BC滑面5.277 5×106N）比较接近；AB滑面有限元计算的夹层底面切向合力和BC滑面有限元计算的夹层底面切向合力不等于0，但2个切向合力基本处于自平衡状态，如表2中，AB滑面有限元计算夹层底面切向合力为1.316 8×106N，BC滑面有限元计算夹层底面切向合力为－1.300 9×106N。由分析还可见，如果将夹层进一步细分为两层夹层，在夹层中面的法向合力更接近于扬压力标准值，但夹层顶面（靠近滑块的面）的法向合力与扬压力标准值差异较大。

（3）由工况21a和工况21b对比可见，相对于采用刚体极限平衡法进行双斜面抗滑稳定分析时，作用在斜面上的扬压力标准值而言，岩基全区域作用浮力时计算的滑面法向合力，较仅滑块作用浮力时计算的滑面法向合力的精度差。对比工况21和工况22可见，岩基全区域作用浮力和水平向渗流力时计算的滑面的法向合力，较仅滑块作用浮力和水平向渗流力时计算的滑面法向合力的精度差。由工况22和工况23对比可见，由于作用在滑块ABCDA上的水平向渗流体积力的合力为0.5ρgHy，将这个合力直接按三角形分布作用在BD面上，其引起的滑面上的法向合力和扬压力法向标准值十分接近，而且夹层底面的切向合力基本处于自平衡状态。

（4）由表3可见，扬压力作为面荷载作用在滑块上引起的大坝位移，和扬压力作为体积力作用在滑块上引起的大坝位移不一样；但从工况22和工况23对比来看，作用在滑块上的水平向力，按面力作用和按体积力作用，引起大坝的位移相差较小。

（5）综上可见，采用有限元法进行重力坝双斜面深层抗滑稳定分析时，仅在滑块ABCDA上作用由岩基稳定渗流分析计算获得的渗流体积力，相对于在岩基全区域作用由岩基稳定渗流分析计算获得的渗流体积力，前者引起滑面AB和CD上的法向合力较后者更接近于刚体极限平衡法对该重力坝双斜面进行抗滑稳定分析时在滑面上的扬压力标准值。由分析还可见，作用在滑块ABCDA上的水平向合力，无论是以水平向渗流体积力作用在滑块ABCDA上，还是三角形分布面力作用在滑块ABCDA中面BD上，2种不同作用方式引起的滑面上的法向合力接近，而且引起的大坝位移相差也较小。

4 结 语

（1）分析了作用在重力坝双斜面上扬压力的作用方式，认为由于双斜面没有完全贯通，存在阻水效应，斜面上的扬压力是线性减小，而不是线性增大。

（2）采用有限元法进行沿坝基面抗滑稳定分析时，当在坝基面设置夹层单元，同时在坝基附近的混凝土和岩体均采用细网格时，采用扬压力分布线沿建基面向上对折，作为坝体简化的浸润线，浸润线以下的坝体采用浮重度的方式考虑扬压力，以及扬压力作为面荷载作用在夹层单元顶面。2种不同的扬压力作用方式引起的坝基面节点垂直向合力和高斯点垂直向合力，与扬压力标准值接近，但2种不同的扬压力作用方式并不一定引起大坝其余部位相近的位移和应力等。

（3）采用有限元法进行重力坝双斜面深层抗滑稳定分析时，仅在滑块上作用由岩基稳定渗流分析计算获得的渗流体积力，相对于在岩基全区域作用由岩基稳定渗流分析计算获得的渗流体积力，前者引起滑面上的法向合力较后者更接近于刚体极限平衡法对该重力坝双斜面进行抗滑稳定分析时在滑面上的扬压力标准值。由分析还可见，作用在滑块上的水平向合力，无论是以水平向渗流体积力作用在滑块上，还是三角形分布面力作用在滑块垂直面上，2种不同作用方式引起的滑面上的法向合力接近，而且引起的大坝位移相差也较小。

（4）扬压力作为面荷载作用在滑面上，或作为体荷载作用在滑块上，虽然总的作用力近似相等，但由于滑块为变形体，不一定引起相近的效应量（位移和应力等）。其中，在垂直方向分别按面荷载或体荷载作用引起的差异，相对于在水平方向分别按面荷载或体荷载作用引起的差异来说，前者引起的差异较后者引起的差异大一些。

［1］ 张光斗.混凝土重力坝的渗透压力［J］.水利学报，1956，（1）：59－70.（ZHANG Guang dou.FiltrationPressure of Gravity Concrete Dams［J］.Journal of Hy draulic Engineering，1956，（1）：59－70.（in Chinese））

［2］ 潘家铮.论不稳定水头下的坝体扬压力问题［J］.水利学报，1958，（3）：90－111.（PAN Jia zheng.Pore Pres sures and Uplift Forces in Gravity Dams under Varied Water Surface［J］.Journal of Hydraulic Engineering，1958，（3）：90－111.（in Chinese））

［3］ 赵代深.重力坝的水荷载分析［J］.水利学报，1984，（7）：53－61.（ZHAO Dai shen.Analysis of Gravity Dam’s Water Load［J］.Journal of Hydraulic Engineer ing，1984，（7）：53－61.（in Chinese））

［4］ 林绍忠.有限元分析中坝基面和结构面渗透压力的合理模拟［J］.长江科学院院报，1993，10（2）：50－53.（LIN Shao zhong.Simulation of Osmotic Pressure Acting on Planes of Dam Foundation and Structure in FEM［J］.Journal of Yangtze River Scientific Research Institute，1993，10（2）：50－53.（in Chinese））

［5］ 段亚辉，赖国伟.碾压混凝土重力坝失稳破坏机理的初步分析［J］.水利学报，1995，（5）：55－59.（DUAN Ya hui，LAIGuo wei.Study of Failure Mechanism of Roller Compacted Concrete Gravity Dam［J］.Journal of Hydrau lic Engineering，1995，（5）：55－59.（in Chinese））

［6］ 王 媛，速宝玉.坝基应力计算中水荷载的组合方式［J］.勘察科学技术，1995，（3）：3－7.（WANG Yuan，SU Bao yu.Water load Combination Form in the Dam Foundation Stress Calculation［J］.Site Investigation Sci ence and Technology，1995，（3）：3－7.（in Chinese））

［7］ 柴军瑞.混凝土坝水荷载讨论［J］.水电能源科学，2000，18（2）：18－20.（CHAI Jun rui.On the Water Load Borne by a Concrete Dam［J］.Water Resources and Power，2000，18（2）：18－20.（in Chinese））

［8］ 张有天.岩石水力学与工程［M］.北京：中国水利水电出版社，2005.（ZHANG You tian.Rock Hydraulics and Engineering［M］.Beijing：China Water Power Press，2005.（in Chinese））

［9］ 范书立，陈健云，林 皋.渗透压力对重力坝有限元分析的影响研究［J］.岩土力学，2007，28（增刊）：575－580.（FAN Shu li，CHEN Jian yun，LIN Gao.Re search on Action of Seepage Pressure on Gravity Dam in FEM［J］.Rock and Soil Mechanics，2007，28（Sup.）：575－580.（in Chinese））

［10］梁 通，金 峰.基于广义有效应力原理的混凝土坝分析［J］.水力发电学报，2009，28（2）：47－51.（LI ANG Tong，JIN Feng.Analysis on Concrete Dams Based on the Concept of Generalized Effective Stress［J］.Jour nal of Hydroelectric Engineering，2009，28（2）：47－51.（in Chinese） ）

（编辑：刘运飞）

M ethod of Applying Uplift Pressure in the Analysis of Deep Sliding Stability of Gravity dam

HUANG Yao ying1，SHEN Zhen zhong2，ZHENG Hong3
（1.College of Hydraulic＆Environmental Engineering，China Three Gorges University，Yichang 443002，China；2.College ofWater Conservancy and Hydropower Engineering，Hohai University，Nanjing 210024，China；3.State Key Laboratory of Geomechanics and Geotechnical Engineering，Institute of Rock and Soil Mechanics，Chinese Academy of Sciences，Wuhan 430071，China）

Finite elementmethod often brings about errors in the calculation of uplift pressure.In view of this，two action modes of uplift pressure in the analysis of the deep sliding stability of double inclined planeswere compared and analyzed.Then themethods of applying uplift pressure when analyzing the sliding stability of double inclined planes and gravity dam’s foundation planes using finite elementmethod were researched.It’s found that uplift pressure，as surface load acting on the slip surface or as body load acting on the sliding block，though with approxi mately equal total force，doesn’t necessarily cause similar effect quantity（displacement and stress，etc）because sliding block is the deformation body.The difference caused by applying surface load or body load in the vertical direction is larger than that in the horizontal direction.

uplift pressure；gravity dam；FEM；dam foundation surface；double inclined planes

TV642.4；TV314

A

1001－5485（2013）12－0112－06

10.3969／j.issn.1001－5485.2013.12.021 2013，30（12）：112－117

2012－11－13；

2012－11－27

国家自然科学基金项目（51209124）；湖北省教育厅科学技术项目（D20101207）

黄耀英（1977－），男，湖南郴州人，副教授，博士，主要从事大坝安全监控及数值计算，（电话）13997662901（电子信箱）huangyaoying＠sohu.com。