基于复合单元法的含层面碾压混凝土坝温度场研究

张石虎，傅少君，陈胜宏

（武汉大学a.水资源与水电工程科学国家重点实验室；b.土木建筑工程学院，武汉 430072）

基于复合单元法的含层面碾压混凝土坝温度场研究

张石虎a，b，傅少君a，b，陈胜宏a

（武汉大学a.水资源与水电工程科学国家重点实验室；b.土木建筑工程学院，武汉 430072）

基于复合单元法的基本原理和不稳定温度场的隐式解法，推导了含有层面的混凝土温度场分析复合单元法控制方程。该算法可以离散模拟碾压混凝土坝中的层面，又避免了剖分层面网格的繁琐的前处理。除此之外，该算法还能整合到传统的有限单元分析程序中，如果某单元不含层面时，它将自动退化为传统的有限单元。基于该算法，建立了老挝南俄5碾压混凝土重力拱坝三维复合单元模型，进行了三维瞬态温度场仿真计算，计算值与监测值在规律和量值上吻合较好。研究结果表明该算法的合理性和在工程应用中具有实用性。

复合单元法；层面；碾压混凝土坝；瞬态温度场

1 研究背景

由于采用逐层碾压的施工方式，碾压混凝土坝身存在施工层面以及层间结合现象。层面不仅影响大坝的变形和渗流，也影响大坝温度场和温度应力分布［1－3］。碾压混凝土上下层温差是碾压混凝土坝温度控制的重要参数［4］，层间的抗拉强度较低［5］，当层面温度骤降时易被拉裂［6－7］。在对碾压混凝土施工期、运行期仿真计算时，合理模拟层面的温度效应是非常重要的。

在传统的有限元分析中，对碾压混凝土层面的模拟可以归为2大类［8－10］：一类是认为层面为无厚度的结构面，沿层面只布置一层节点，其初始温度为新老混凝土的平均温度，该方法不能模拟此处温度的不连续性以及浇筑结合后层面温度达到平衡的过程；另一类是认为层面为一个渐变过渡层，沿层面布置2层节点，但是层面厚度及层面的热力学参数一般难以确定，且前处理十分繁琐。碾压混凝土坝施工层薄，采用常规有限单元法进行施工仿真计算时，网格划分十分密集。同时，当施工方案出现变更时，需变更相应计算模型，对于常规有限单元法而言，需重新划分计算网格，工作量庞大并且繁琐。

复合单元法是陈胜宏等［11］提出的一种新的数值模拟方法，它吸收了数值流形方法、块体单元法、有限单元法等方法的优点，能够应用于连续变形分析和不连续变形分析。复合单元法已经逐步应用到应力场分析［12－13］、渗流场分析［14－15］、应力－渗流耦合分析［16］等研究领域，但是复合单元法在温度场方面的研究才刚刚起步。复合单元法在处理含有不连续面的问题时拥有独特的优势，本文基于复合单元法，根据变分原理，推导出含层面的复合单元法温度控制方程。对于含较多层面的碾压混凝土坝，划分网格的限制减小，前处理难度降低。层面由拓扑程序自动生成，当碾压混凝土结构变化时，可以方便地对模型进行修改和计算，不必重新划分网格，为前处理提供了较大的便利。并且复合单元可以整合到常规有限单元法分析中，当层面上下温度稳定且相等时，复合单元即可退化为常规有限元。

2 基本概念

复合单元法使用的网格与常规有限单元法相似，首先，不考虑层面的影响，单元尺寸和分布依据结构的形状和温度梯度而定，将研究对象离散成普通的有限元网格。然后，根据层面的空间信息和有限元网格进行代数和集合运算，得到复合单元网格信息［17］。在新的网格系统中，有一部分单元含有一个或者多个层面，这部分单元成为复合单元，被层面划分的子域称为子单元。

如图1所示为含nc个子单元，nc－1个层面的复合单元模型，每个子单元和层面可以有不同的热学参数和浇筑时间，每个子单元内的温度均由相应的节点温度插值。

图1 含nc个子单元的复合单元Fig.1 Composite element including ncsub elements

每个子单元内的温度由复合单元的节点温度插值得到，且插值表达式仅在相应的子单元内有效，其插值函数是常规有限元法中定义的形函数，此时复合单元的自由度是传统有限单元的nc倍。当碾压混凝土坝采用斜层碾压的施工方式时，每一个层面需要建立其局部坐标系，层面的局部坐标系，如图2所示，定义层面的倾向为j，倾角为θj，zj垂直于层面指向上方的法线方向，yj指向层面倾角方向，xj与zj，yj轴垂直，其指向由右手螺旋法则确定。层面j的局部坐标系与整体坐标系的转换关系为

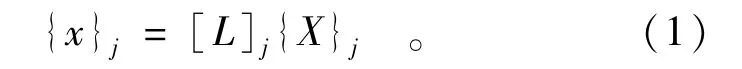
式中：｛x｝j为层面的局部坐标系；｛X｝j为整体坐标系；［L］j为倾向j和倾角θj的函数。

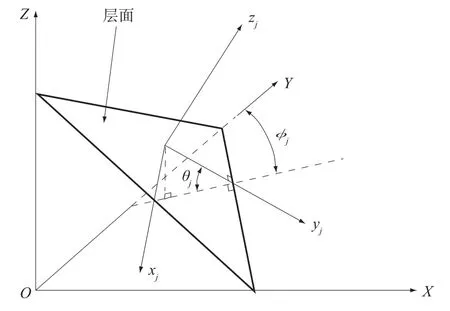
图2 层面的局部坐标系Fig.2 Local coordinates of lift interface

3 控制方程与算法

一个含有nc个子单元的复合单元三维瞬态温度场的热传导方程可表示为

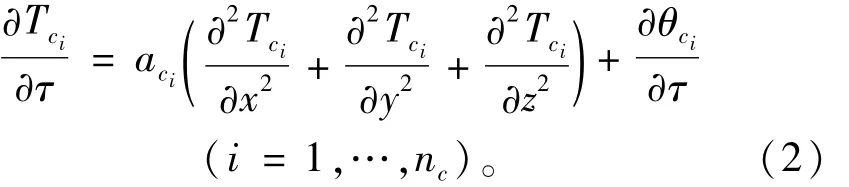
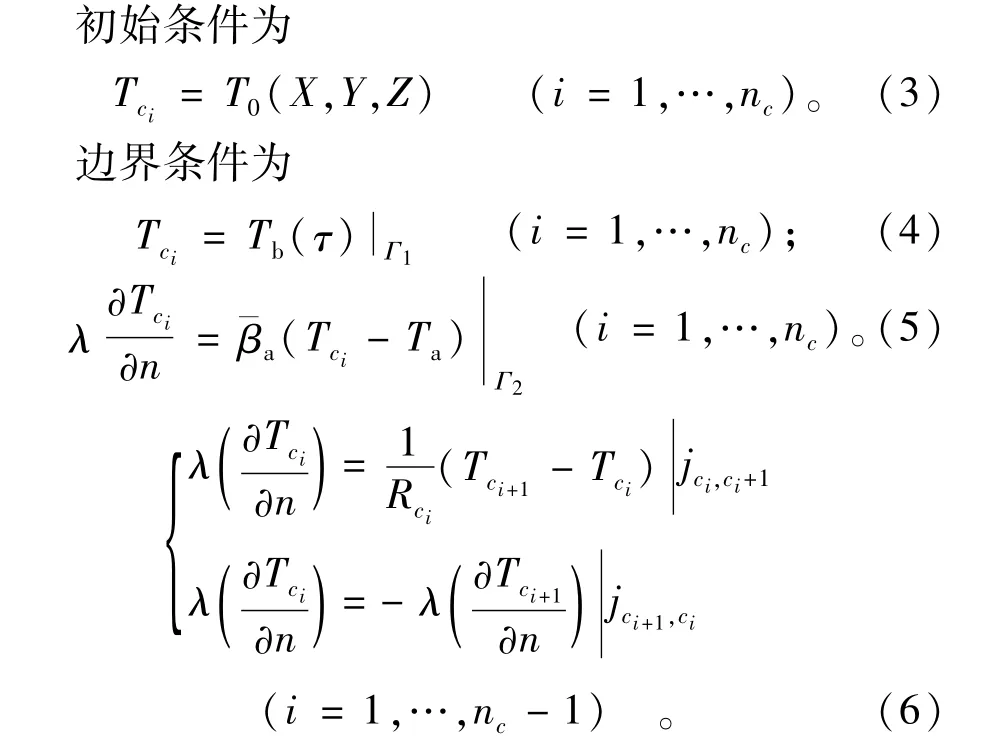
式中：aci为子单元的导温系数（m2／d）；τ为时间（d）；θci为子单元的绝热温升（℃）。上述边界公式中：λ为导热系数（kJ·（m·d·℃）－1）；n为垂直于边界面或者层面的法线方向；T0为初始温度值（℃）；Tb为边界处的温度值（℃）；Ta为大气温度（℃）；珔βa为与空气接触换热系数（kJ·（m2· d·℃）－1）；Rci为子单元之间的接触热阻（m2·d·℃· kJ－1）。

利用变分原理在空间上进行离散，可得到子单元ci的泛函：

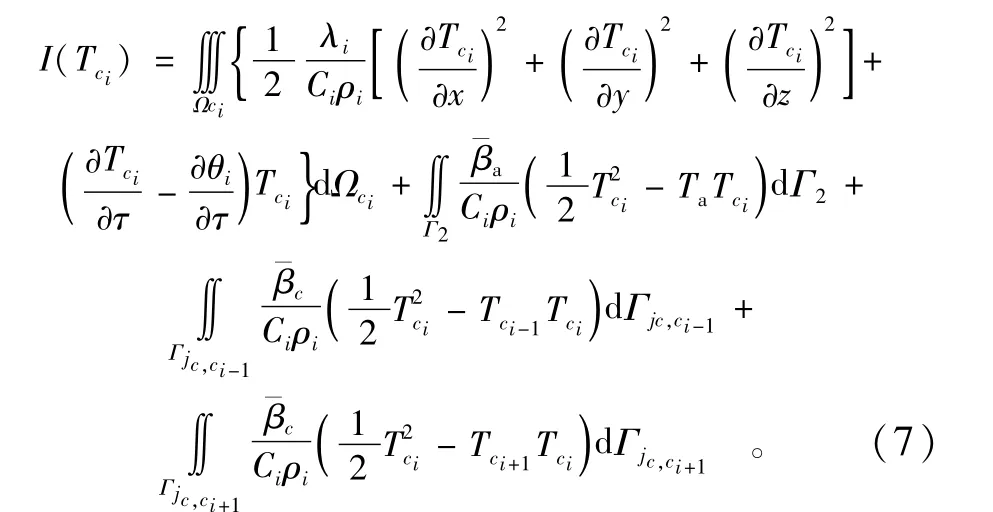
式中：Γ2表示子单元中与空气直接接触对流表面；Γci，ci－1表示子单元ci与ci－1的接触传热面；Γci，ci＋1表示子单元ci与ci＋1的接触传热面；珔βc为子单元之间的接触换热系数（kJ·（m2·d·℃）－1）；Ci为比热容（kJ·（kg·℃）－1）；ρi为密度（kg·m－3）。则有

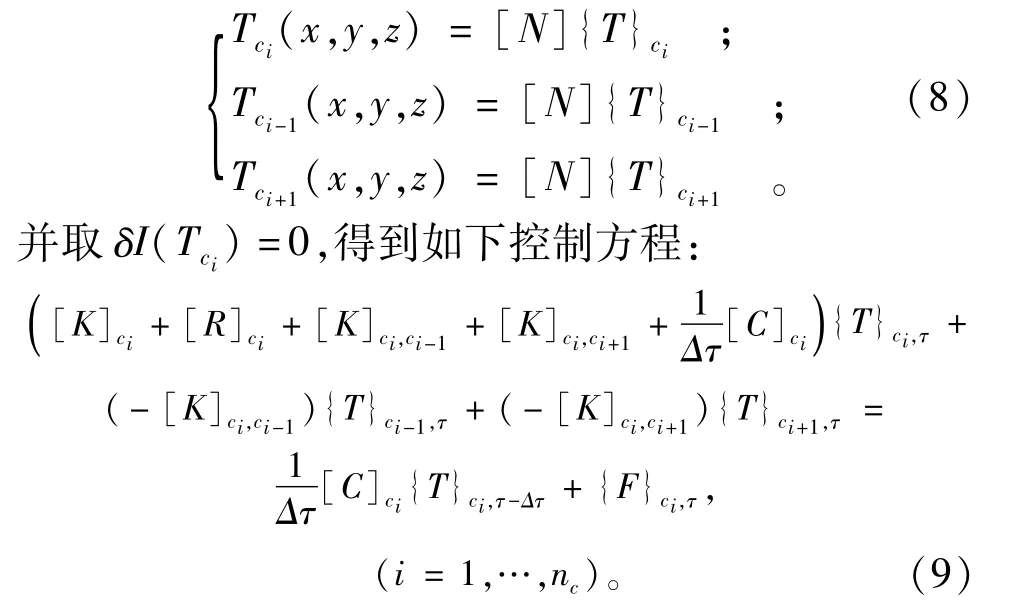
其中，

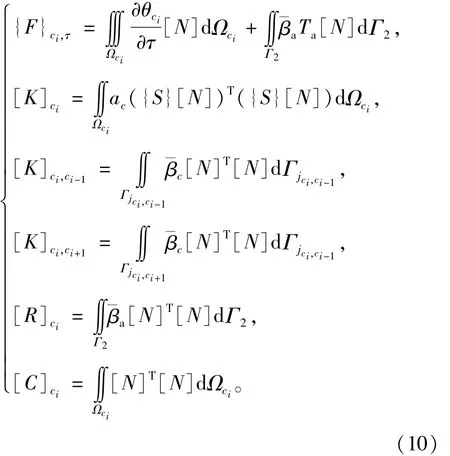
将上述各子单元的传导矩阵和右端项联立，即可得含多个层面的复合单元的基本计算方程组：

其中，

由上式可以看出，复合单元控制方程的格式和常规有限元格式相似，可以无缝接入常规的有限元整体刚度矩阵中，只是当一个复合单元含有nc－1个层面时，节点自由度由常规有限元的1组变成了nc组。当复合单元不含有层面或者各个子单元温度趋于稳定不再需要考虑层面效应时，复合单元也可以自动退化为常规的有限单元。于是，在程序的编制和求解方程组时，复合单元法可以很方便地和常规有限元整合在一起。

4 工程应用

4.1 工程背景与浇筑情况

老挝南俄5水电站位于老挝南俄河上游右岸支流Nam Ting河上。水库正常蓄水位1 100 m，电站首部枢纽由碾压混凝土重力拱坝和电站进水口等建筑物组成，最大坝高100.5 m，本工程已于2010年初开始浇筑大坝混凝土，至2011年10月底大坝碾压混凝土浇注至1 089.7 m高程。

4.2 计算模型参数与边界条件

4.2.1 计算模型和热学参数

根据提供的坝体体型资料建立了三维复合单元网格，为了对浇筑过程进行准确模拟，浇筑层的厚度取0.5 m左右。如图3所示，模型共含有18 260个复合单元，38 282个节点。坝体的混凝土热学参数如表1所示。

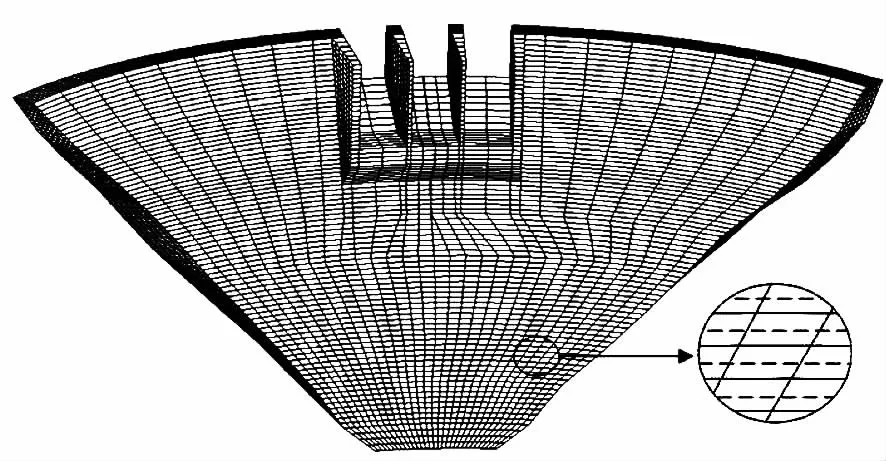
图3 三维复合单元网格Fig.3 Three dimensional composite elementmeshes

4.2.2 计算边界条件

模型中与基岩接触的面施加绝热边界，坝体上下游施加气温的对流边界，并且边界条件是一个随着浇筑过程动态变化的过程。根据气温监测资料，气象站气温监测值与拟合值对比曲线如图4所示，拟合的气温公式为

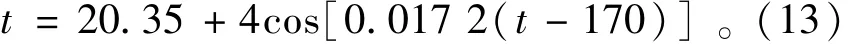
式中t为距起算时间2010年1月10日的天数。

4.3 计算结果与分析

4.3.1 温度场仿真结果与分析

根据上述的边界条件对坝体温度场进行仿真计算，计算截止时间为2012年的2月20日（最后一个浇筑块完成时刻）。分别在坝体1 063.5 m和1 081 m高程处选取了T1－13和T2－10两个典型测点，提供的监测资料截止到2011年11月19日。测点处计算值和监测值对比曲线如图5所示。

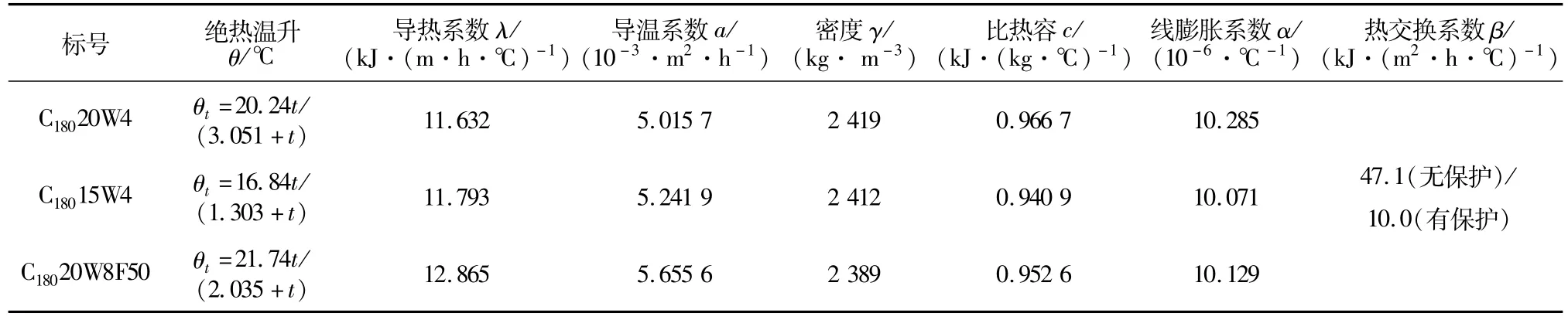
表1 混凝土热学参数Table 1 Thermal parameters of concrete

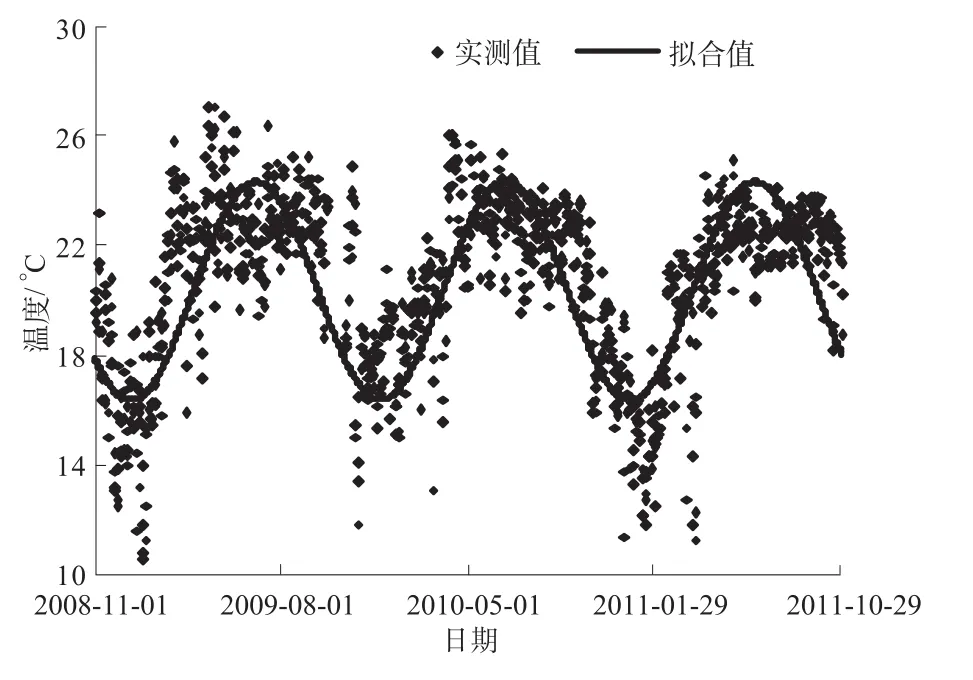
图4 气温时程曲线Fig.4 Time history curve of atmospheric tem perature

图5 温度时程曲线Fig.5 Time history curves of tem perature

（1）由图5可以看出，测点处温度的计算值和监测值变化规律是一致的，并且两者量值的差别较小，浇筑初期两者差异在2.5℃以内，后期差异保持在1℃以内，说明复合单元法研究含有层面碾压混凝土坝温度场是可行的。

（2）T1－13测点位于其浇筑层上部接近表面处，由图5（a）可以看出，浇筑初期受水化热的影响温度迅速上升至30℃左右，但是由于距离边界较近，受空气热对流影响，测点温度又迅速下降至23℃左右；随着新浇筑层的碾压形成，受到新浇筑层水化热影响，测点处又迅速上升至32℃，随后依靠自身的热传导逐渐冷却，最终达到稳定温度。

（3）T2－10测点位于其浇筑层的中下部，由图5（b）可以看出，浇筑初期水化热反应迅速温度很快上升至40℃左右，由于测点距离边界处较远，受到空气和上层浇筑层影响较小，测点处温度值依靠自身热传导开始缓慢冷却最终达到稳定温度。

由图6可以看出，坝体剖面温度场的分布符合一般规律，截至2012年2月20日，温度最大值出现在1 025 m高程内部，量值在34℃左右。从内部逐渐移动到边界处，温度值逐渐减小并达到19℃左右。

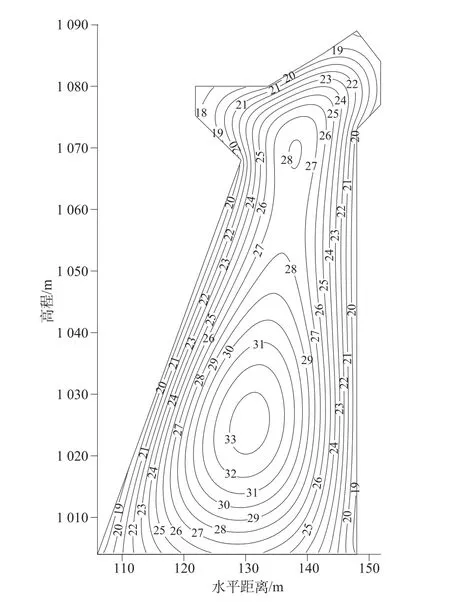
图6 坝右0＋000.0剖面温度等值线图（2012－02－20）Fig.6 Tem perature contours on p rofile 0＋000.0 in the right bank of dam（2012－02－20）

5 结 语

本文基于复合单元法，根据变分原理，推导出了含层面的复合单元法温度控制方程。将众多层面子单元内含在了普通有限单元中，使得前处理的难度大大降低，将复杂繁琐的层面传导矩阵形成工作交给计算机。复合单元法和有限单元法程序可以无缝结合。以老挝南俄5碾压混凝土坝为例，进行了坝体温度场的仿真，计算值和监测值在规律和量值上吻合都比较好，说明了含有层面复合单元法的合理性和实用性。考虑到层面附近温度变化较剧烈，温度梯度较大，将P型自适应技术引入到含有层面的复合单元法中，不改变网格情况下将提高计算的精度，后续工作将对此进行进一步的研究。

［1］ 朱伯芳，许 平.碾压混凝土重力坝的温度应力与温度控制［J］.水利水电技术，1996，（4）：18－25.（ZHU Bo fang，XU Ping.Thermal Stresses and Temperature Control of RCC Gravity Dam［J］.Water Resources and Hydropower Engineering，1996，（4）：18－25.（in Chi nese））

［2］ 朱伯芳.大体积混凝土温度应力与温度控制［M］.北京：中国电力出版社，1999.（ZHU Bo fang.Thermal Stresses and Temperature Control of Mass Concrete［M］.Beijing：China Power Press，1999.（in Chinese））

［3］ 苏培芳，汪卫明，陈胜宏.碾压混凝土重力坝全程综合仿真分析与安全评估［J］.岩土力学，2009，30（6）：1769－1774.（SU Pei fang，WANG Wei ming，CHEN Sheng hong.Integrated Simulation and Safety Assessment for RCC Gravity Dam on Rock Foundation during Whole Process of Construction［J］.Rock and Soil Mechanics，2009，30（6）：1769－1774.（in Chinese））

［4］ 黄达海，宋玉普，赵国藩.碾压混凝土坝温度徐变应力仿真分析的进展［J］.土木工程学报，2000，33（4）：97－100.（HUANG Da hai，SONG Yu pu，ZHAO Guo pan.Advancement of Thermal Creep Stress Analysis for RCCDam［J］.China Civil Engineering Journal，2000，33（4）：97－100.（in Chinese））

［5］ 张国新.碾压混凝土坝的温度控制［J］.水利水电技术，2007，（6）：32－38.（ZHANG Guo xin.Temperature Control of RCC Dam［J］.Water Resources and Hydro power Engineering，2007，（6）：32－38.（in Chinese））

［6］ 黎展眉.普定碾压混凝土拱坝裂缝成因探讨［J］.水力发电学报，2001，（1）：96－102.（LIZhan mei.The Pilot Study of Causes of Cracks in Puding RCC Arch Dam［J］.Journal of Hydroelectric Engineering，2001，（1）：96－102.（in Chinese））

［7］ 朱伯芳.混凝土坝温度控制与防止裂缝的现状与展望［J］.水利学报，2006，37（12）：1424－1432.（ZHU Bo fang.Current Situation and Prospect of Temperature Control and Cracking Prevention Technology for Concrete Dam［J］.Journal of Hydraulic Engineering，2006，37（12）：1424－1432.（in Chinese））

［8］ 顾冲时，黄光明，赖道平.碾压混凝土坝施工层面变形分析模型［J］.应用数学和力学，2007，（1）：70－76.（GU Chong shi，HUANG Guang ming，LAI Dao ping.Analytic Model of Deformation of Construction Interfaces of RCC Dam［J］.Applied Mathematics and Mechanics，2007，（1）：70－76.（in Chinese））

［9］ 顾冲时，程乐群，李婷婷.探讨碾压混凝土坝薄层单元有限元分析法［J］.计算力学学报，2004，21（6）：718－721.（GU Chong shi，CHENG Le qun，LI Ting ting.Study on Thin Layer Element and Application in FEM A nalysis of RCC Dams［J］.Chinese Journal of Computa tional Mechanics，2004，21（6）：718－721.（in Chi nese））

［10］黄达海，杨生虎.碾压混凝土上下层结合面上初始温度赋值方法研究［J］.水力发电学报，1999，（3）：25－34.（HUANG Da hai，YANG Sheng hu.A Study on the Methods of Setting Initial Temperature on the Joint Face of Roller Compacted Concrete［J］.Journal of Hydroelec tric Engineering，1999，（3）：25－34.（in Chinese））

［11］陈胜宏，强 晟，陈尚法.加锚岩体的三维复合单元模型研究［J］.岩石力学与工程学报，2003，22（1）：1－8.（CHEN Sheng hong，QIANG Sheng，CHEN Shang fa.Study on the Three Dimensional Composite Element Mod el of Bolted Rock Masses［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22（1）：1－8.（in Chi nese））

［12］CHEN SH，QIANG S，CHEN S F，et al.Composite Ele ment Model of the Fully Grouted Rock Bolt［J］.Rock Mechanics and Rock Engineering，2004，37（3）：193－212.

［13］CHEN SH，QIANG S.Composite ElementModel for Dis continuous Rock Masses［J］.International Journal of Rock Mechanics and Mining Sciences，2004，41（5）：865－870.

［14］CHEN S H，FENG X M.Composite Element Model for Rock Mass Seepage Flow［J］.Journal of Hydrodynamics，2006，18（2）：219－224.

［15］CHEN SH，XUE L L，XU G S，et al.Composite Element Method for the Seepage Analysis of Rock Masses Contai ning Fractures and Drainage Holes［J］.International Journal of Rock Mechanics and Mining Sciences，2010，47（5）：762－770.

［16］薛娈鸾，陈胜宏.岩石裂隙渗流与法向应力耦合的复合单元模型［J］.岩石力学与工程学报，2007，26（增1）：2613－2619.（XUE Luan luan，CHEN Sheng hong.Com posite Element Model of Seepage Normal Stress Couplingfor Rock Fractures［J］.Chinese Journal of Rock Mechan ics and Engineering，2007，26（Sup.1）：2613 2619.（in Chinese））

［17］QIANG S，ZHANG Y，ZHU Y M，et al.Research on the Pre process of Three Dimensional Composite Element Method for Discontinuous Rock［C］∥Proceedings of the 6th European Conference on Numerical Methods in Geotechnical Engineering.Graz，Austria，September 68，2006.London：Taylor and Francis Group，2006：283 288.

（编辑：黄 玲）

Research on Tem perature Field of RCC Dam Containing Lift Interfaces by Composite Element M ethod

ZHANG Shi hu1，2，FU Shao jun1，2，CHEN Sheng hong1
（1.State Key Laboratory ofWater Resources and Hydropower Engineering Science，Wuhan University，Wuhan 430072，China；2.School of Civil Engineering，Wuhan University，Wuhan 430072，China）

According to the principle of composite elementmethod（CEM）and the implicit expression of transient temperature field，the thermal governing equations of CEM formass concrete containing lift interfaces are deduced.The effect of each lift interface can bewell simulated and the difficulty of generatingmeshes around the lift interface is overcome.This algorithm can be incorporated into the conventional finite element analysis program.The element containing no lift interfacewill be degenerated to traditional finite element automatically.By using this algorithm，a three dimensional composite elementmodel of Laos Nam Ngum5 RCC gravity dam is established.The three dimen sional transient temperature field is simulated.The computational results agree with themonitored values very well in terms of variation regularity and quantity.The research results indicate that this algorithm is valid and practical in engineering application.

composite elementmethod；lift interface；RCC dam；transient temperature field

TV642

A

1001－5485（2013）12－0101－06

10.3969／j.issn.1001－5485.2013.12.019 2013，30（12）：101－106

2012－11－02；

2013－01－05

中央高校基本科研业务费专项（2012210020204）

张石虎（1987－），男，河南濮阳人，博士研究生，主要从事工程数值计算与分析方面的研究，（电话）027－68776698（电子信箱）hu hu1066＠126.com。

傅少君（1969－），男，重庆市人，教授，博士生导师，主要从事工程数值计算与分析方面的研究，（电话）027－68776698（电子信箱）shaojunfu69＠vip.sina.com。