低碳经济下班轮航线配船模型及其算法实现

许 欢,刘 伟,尚雨廷

(上海海事大学交通运输学院,上海200135)

低碳经济下班轮航线配船模型及其算法实现

许 欢*,刘 伟,尚雨廷

(上海海事大学交通运输学院,上海200135)

考虑到航速变化对航线配船决策所产生的非线性影响,推导了船舶航速与船舶往返航次时间、航次成本及航线配船数之间的数学关系式,把船舶航速作为决策变量引入传统的航线配船模型中,并且把船队的二氧化碳排放量作为优化目标之一,建立船队利润最大与碳排放量最小两个目标最优的双目标航线配船模型.针对模型非线性和混合整数解的特点,采用LINGO11.0优化平台,自编程序,应用分支定界算法,进行仿真算例研究.结果表明,该模型可以同时决策航线配船和船舶航速,其优化结果更符合实际情况,同时更有利于运力的有效利用,船舶燃油消耗的节省和碳排放的减少.

水路运输;航线配船;LINGO;航速;低碳经济

1 引 言

研究报告显示,航运业目前每年排放的二氧化碳超过12亿t,约占全球碳排放总量的4%[1].海运业的碳排放问题越来越引起人们的关注,国际社会也表达了减少海运业碳排放的决心.目前来看,减速航行是短期内显著减少船舶碳排放的有效措施.而船舶航速是班轮航线配船的影响因素之一,它不仅直接影响到船舶往返航次时间,而且影响到航次成本的计算及航线配船数,但是以往的航线配船模型中往往将船舶航速假设为常数,忽略了其对于航线配船决策的影响,并且没有考虑船舶的碳排放问题.文献[2-6]对航线配船问题进行了定义,并探讨了该问题的求解方法;文献[7,8]为国内航线配船问题的研究奠定了基础;文献[9-11]对航线配船模型的优化进行了研究和探讨,并且将优化目标从船队营运成本的最小化过渡到更为合理的船队经营利润最大化,分别建立了线性规划、非线性规划和动态规划模型,在实践及理论方面取得了许多有益成果;文献[12]对不确定情况下航线配船问题进行了探讨,拓展了航线配船问题的研究范畴;文献[13]为弥补目前航线配船问题研究存在的不足,以最大化船公司航线运营利润、最小化运力浪费为目标,建立双目标航线配船模型,通过遗传算法在解空间内的遍历和搜索,得到问题的满意解,并用实例证明了模型的可行性和算法的有效性.

这些研究主要以船队盈利或节省成本为优化目标,忽略了船舶航速的影响,将问题简单地处理为线性模型.这类模型都将船舶航速假定为常数,相应地,船舶往返航次时间和航次成本被当作常数.但实际情况往往并非如此,船舶航速并不是一成不变的.特别是在当前低碳经济时代,减速航行已成为船舶节能减排的重要手段.由于船舶的燃油消耗量和往返航次时间与航速之间存在着函数关系,因此当航速变化时,船舶的航次燃油成本和往返航次时间也会随之变化.如果还将其作为定值处理,求得的最优解会偏离实际情况.为了修正这种偏差,本文在传统的线性规划模型基础上,考虑船舶航速变化对航线配船决策产生的非线性影响,并且把船队的二氧化碳排放量也作为优化目标之一,尝试建立船队利润最大与碳排放量最小两个目标最优的双目标航线配船模型,并设计了模型的求解方法.

2 模型建立

2.1 模型假设

在由多港口组成的航线网络上,多船舶航线配船问题较为复杂.在建立具体的数学模型之前,做以下基本假设:

(1)研究期内企业不进行新船建造投资;

(2)研究期前的投资费用是已经确定的沉没成本,研究期内做的任何决策对它们都无影响,故在配船决策时不考虑这部分费用;

(3)船队承担运输任务的航区由若干装货港和若干卸货港组成,共形成G条有货运任务的航线,船舶以简单航次形式运输货物;

(4)研究期内欲营运的航线及挂靠港口的顺序已经确定;

(5)在给定航线的各港口对之间,已预测出年货运需求量,每条航线上的所有运输需求都必须被满足;

(6)在研究期内共有k种船型可供选择,同一航线上配置相同类型的船舶营运;

(7)研究期内船队规模不发生变化,即不存在新造船及退役船舶,并且不考虑船舶的租赁,包括出租和承租;

(8)研究期内各航线上的运价为已知;

(9)船舶载运能力及船舶在港口对之间承运的货物均以吨或集装箱数计量,货物若以集装箱装运,则采用整箱形式;

(10)研究期内同一航线上的发船频率相同,船舶以规则的间隔到港装卸货物,一个航次只能由一艘船舶执行,船舶在研究期内运行的船期表不变;

(11)研究期为一年.

2.2 模型参数

(1)决策变量.

Vjh——研究期内第j型船在第h航线上的营运航速;

xjh——研究其内在h航线上配置的j型船的数量,整数变量;

Oj——研究期内第j型船闲置的数量,整数变量.

(2)模型参数.

Z——船队总利润;

Uj——第j型船的额定载箱量;

rjh——第j型船在第h航线上的平均舱位利用率;

Pjh——第j型船在第h航线上的运价;

Rjh——第j型船在第h航线上的年营运费用;

Fj——第j型船年闲置费用;

Wh——h航线上年货运需求量;

Aj——刚进入研究期时,即年初船队中拥有的j型船数量;

Qjh——每艘第j型船在第h航线上完成的年货运量.

2.3 模型建立

传统的航线配船模型[14]

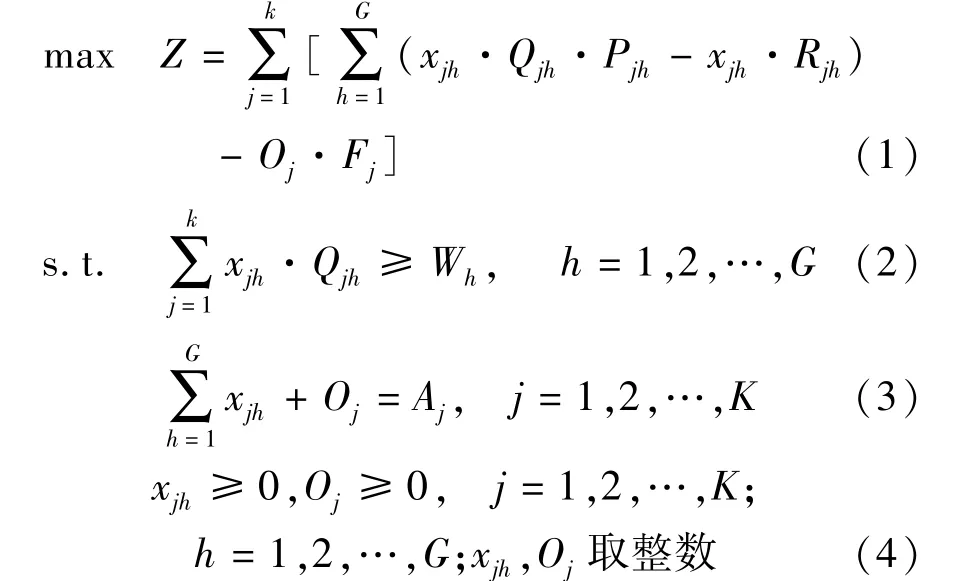
式(1)为船队总利润最大化;式(2)保证船队完成研究期内各航线的货运任务,即货运量约束;式(3)保证分配在各航线上的某船型的数量之和与船队中拥有的各船型的数量相等,即运力约束;式(4)保证决策变量的非负性.

显然这个模型没有考虑到航速对于航线配船决策的影响,目标函数也比较单一,不适应低碳经济的发展趋势,下面对此模型进行改进.

2.3.1 航速与航次时间及航线配船数的关系

设t0jh为第j型船在第h航线上每往返航次的停泊时间,它取决于船舶j的航次载货量及挂靠港的装卸效率;t1h为第h航线的发船间隔,它取决于船公司的服务频率;为第h航线的船舶平均往返航次时间,它取决于航线距离、船舶的航行速度和停泊时间,即

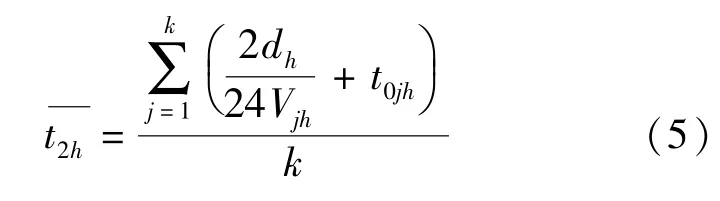
式中 dh——第h航线的距离.

根据赵刚的《国际航运管理》[14],航线h的配船数为

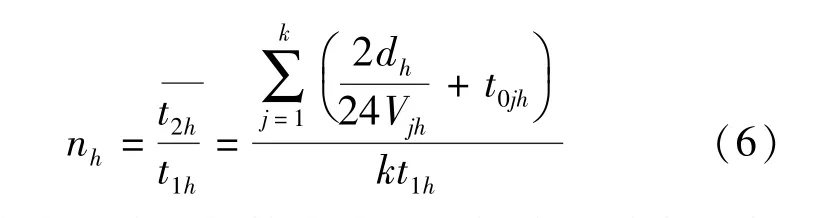
而航线h的配船数为分配到航线h的各种船型的数量之和,即

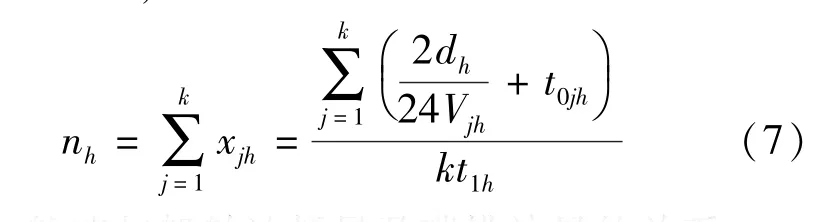
2.3.2 航速与船舶油耗量及碳排放量的关系

Hughes[15]在1996年的研究表明:船舶的燃油消耗与航速的立方成正比,该定理被普遍接受,并且应用在策略层面上进行油耗分析,因此本文采用油耗与航速之间的这种幂函数关系进行研究.

第j型船在第h航线上每往返航次的单船油耗量可表示为

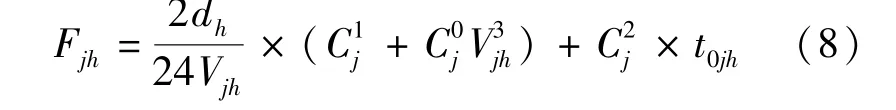
j船型的年营运天数用Tj表示,则每年每艘j型船在h航线上可完成的航次数可以表示为

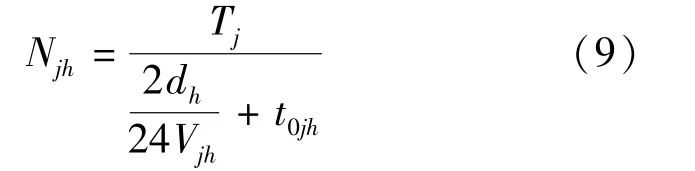
整个船队全年的燃油消耗量可用表示为

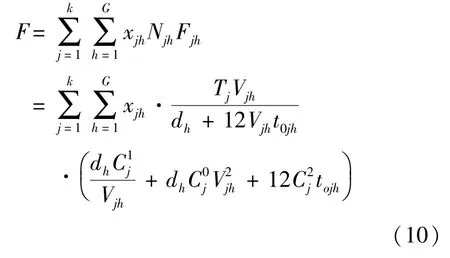
将式(10)乘上CO2的转化系数(这里采用IPCC的系数,即1 t船用燃油产生3.17 t CO2[16]),得到另一目标函数2.3.3 航速与营运成本的关系

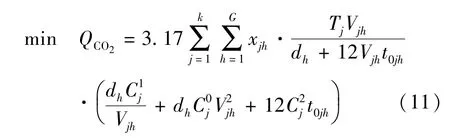
由于燃油成本在船舶总营运成本中占有很大的比例,即船舶营运成本与船舶营运航速存在一定的数量关系,所以原目标函数也应相应的进行改进.用Rjh0表示第j型船在第h航线上单船年营运成本(燃油成本除外),Rjh1表示第j型船在第h航线每年的单船燃油成本.则Rjh=Rjh0+Rjh1,其中

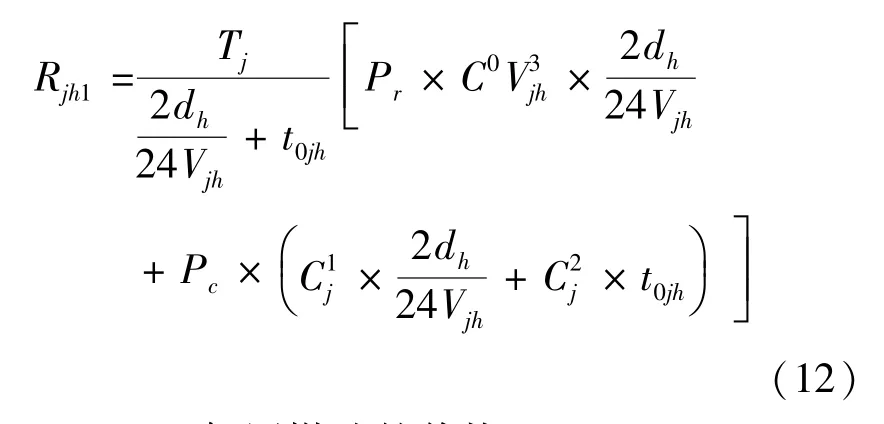
式中 pr——船用燃油的价格;

pc——船用柴油的价格.则原目标函数可以改写为

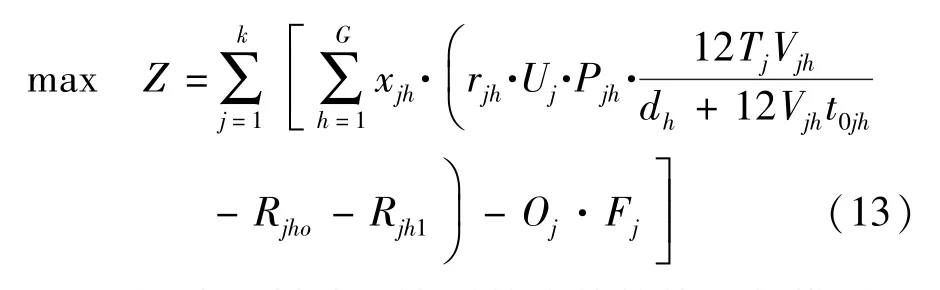
由此,建立低碳经济下的班轮航线配船模型.目标函数 f1:式(13); f2:式(11)

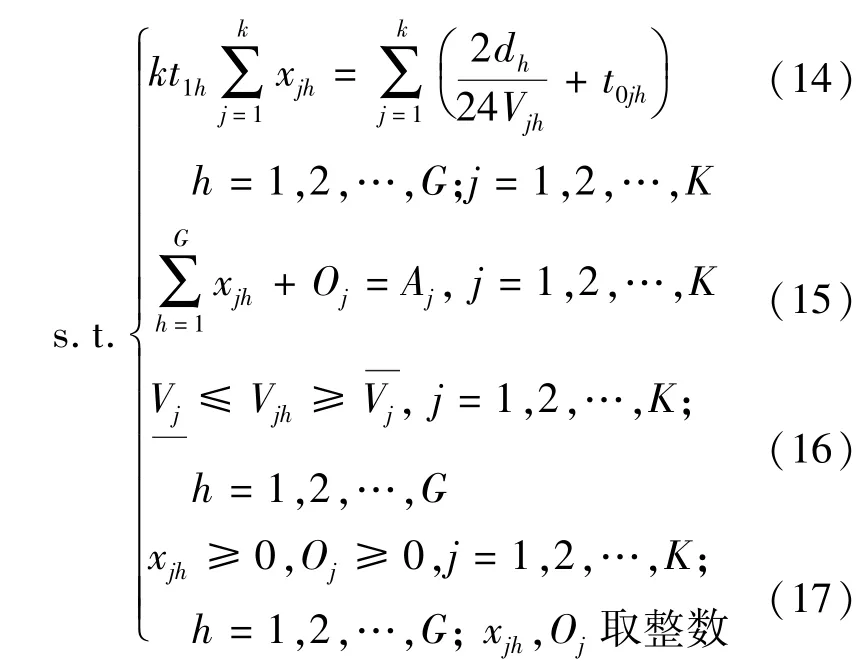
式(14)为航线配船数约束;式(15)为船舶运力约束;式(16)为船舶航速约束,式中分别为j型船的最低航速和最高航速;式(17)保证决策变量的非负性.

3 模型求解

上述模型是一个双目标混合整数非线性规划模型,它同时包含整数型变量和连续型变量(航线配船数xjh为整数型变量,航速Vjh为连续型变量),目标函数和约束条件均具有非线性,这给问题的求解带来了很大困难,且在多目标规划中,极少存在绝对最优解.这是因为在优化过程中,多个目标往往难以同时达到最优,因此在决策优化过程中,我们应当避免最差的结果,寻找其Pareto最优解(有效解)或弱有效解.

多目标规划问题的求解方法有约束法、分层序列法、功能系数法、评价函数法等.针对航线配船的实际情况及该模型的特点,本文采用约束法将双目标规划模型转化成单目标规划模型,即将f1作为主目标函数,将f2进行处理后加入约束条件中.转化的具体方法是:设定一个常数Q,令f2≤Q.Q的取值一般取决于期望目标值,在此模型中可以取政府相关部门规定的碳排放标准或者政府分配给每个航运企业的碳排放配额,由此将双目标模型转化为最终的单目标规划模型.转化后的航线配船模型为

目标函数 f:式(13);

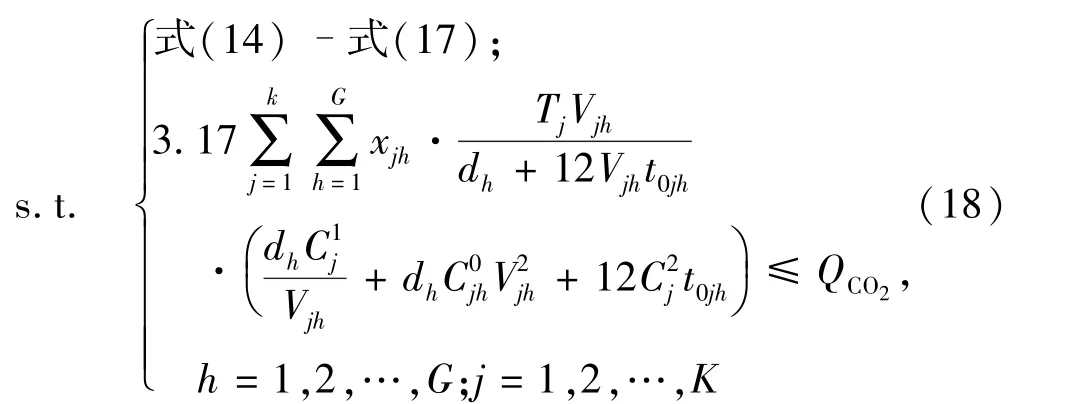
转化后的模型拥有(G+K+1)个约束条件, (2×K×G+K)个变量,仍然属于非线性混合整数规划模型.该类模型是整数规划中的一大类问题,由于问题本身的复杂性,至今没有太多有效的方法.本文将采用LINGO11.0优化平台,自编程序,进行实证算例研究,以证明所构建模型和求解思路的有效性.

4 仿真计算与分析

以某航运公司在未来一年内的航线配船问题为例,其船队及航线的基本情况如表1-表6所示.假设该公司拥有3种船型的船队,即K=3.各型船的年可营运时间为345天,研究期内营运3条航线,即G=3.假设企业拥有剩余运力,并且在未来一年内企业没有新增运力,根据各航线上的货运量预测结果,求出船队在未来一年内的最优航线配船方案.

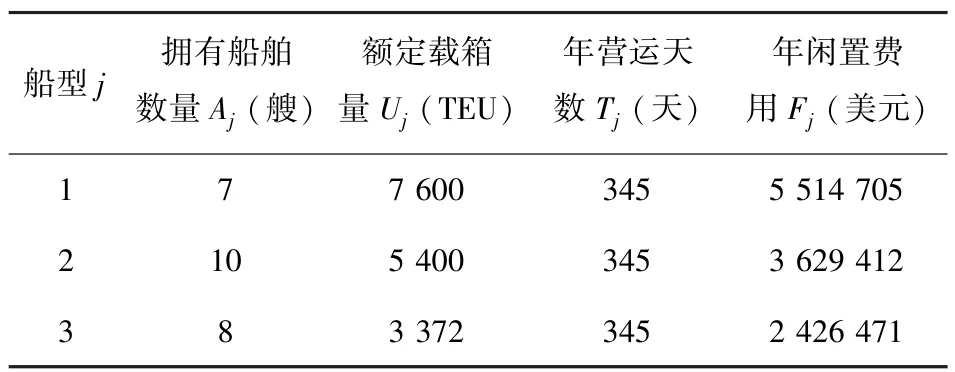
表1 研究期初船队基本情况Table 1 Fleet composition at beginning of the research horizon

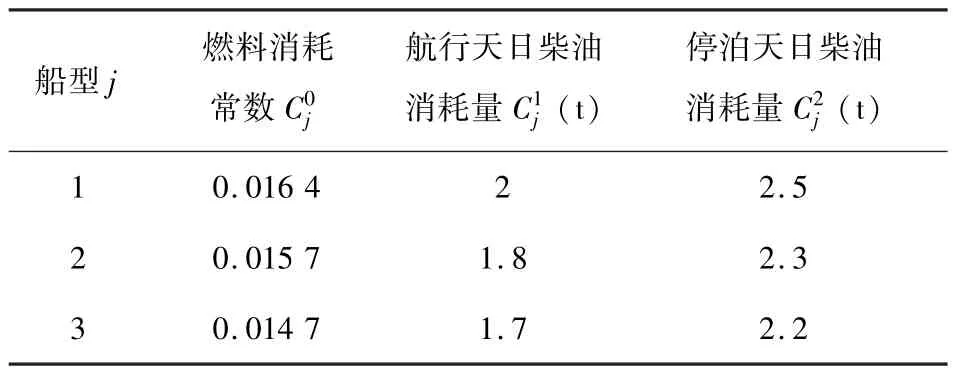
表2 各型船燃油消耗常数Table 2 Constants of fuel consumption for various types of ships

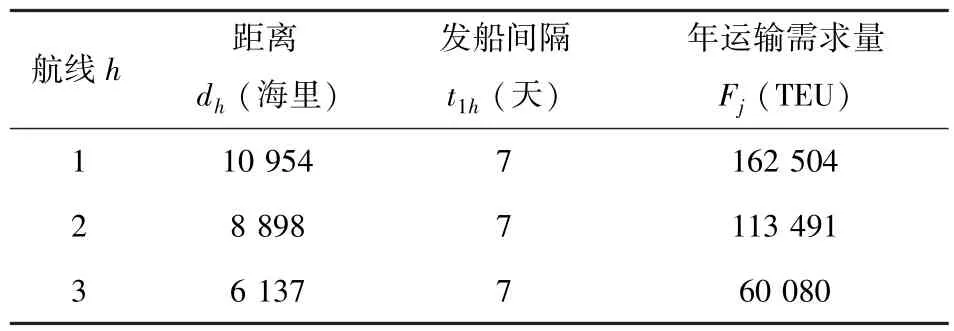
表3 航线情况Table 3 The conditon of the shipping route

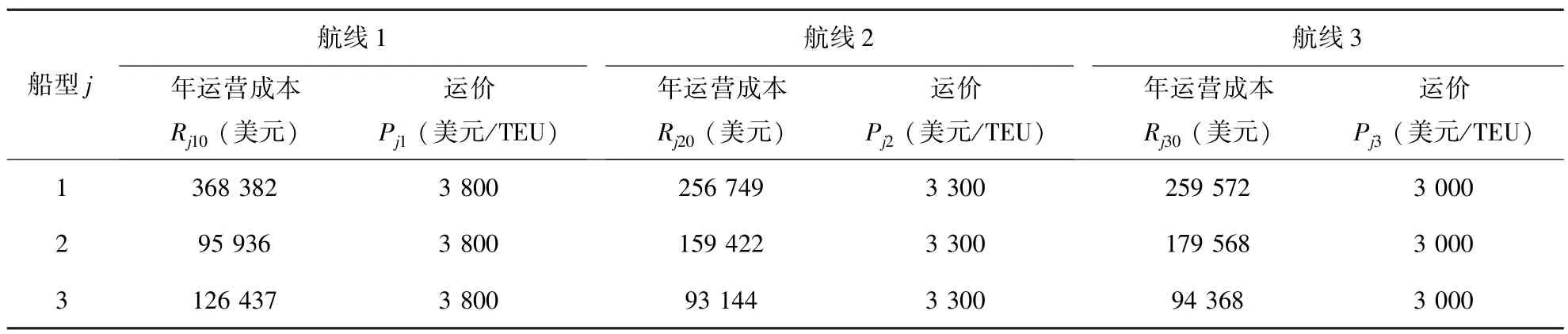
表4 各航线不同船型的年运营成本(燃油成本除外)及运价Table 4 Yearly operational cost(oil cost excluded)and frieight rate of various types of ships on each route

表5 各航线不同型船的平均舱位利用率及航次停泊时间Table 5 Average utilization ratio of the shipping space and the berth time in every voyage for various types of ships on each route

将上述参数输入所编写的LINGO程序,运行后,得到低碳经济下的航线配船方案如表6、表7所示.

经计算在该配船方案下,船队年利润112 993万美元,船队年油耗量为35万t,年二氧化碳排放量为110.8万t.

从该优化结果可以看出,低碳经济下的班轮航线配船模型不仅可以求解出航线配船方案,而且可以计算出船舶在各航线上航行的最佳航速.该模型较全面地考虑了航速与燃油成本、航速与二氧化碳排放、航速与航线配船数之间的关系,反映了船舶航速变化对航线配船产生的非线性影响,优化结果更加符合船队营运的实际情况,更为客观和科学.并且该模型同时考虑了环境效益和经济效益,能够实现节能减排这一可持续发展的目标.对于班轮公司来说,只要根据其船队的实际情况,将对应的参数输入本文所编写的LINGO程序,就可以快速地求解出低碳经济下的航线配船方案,操作简单、方便.

表6 低碳经济下船公司配船方案Table 6 Fleet deployment scheme under low-carbon economy

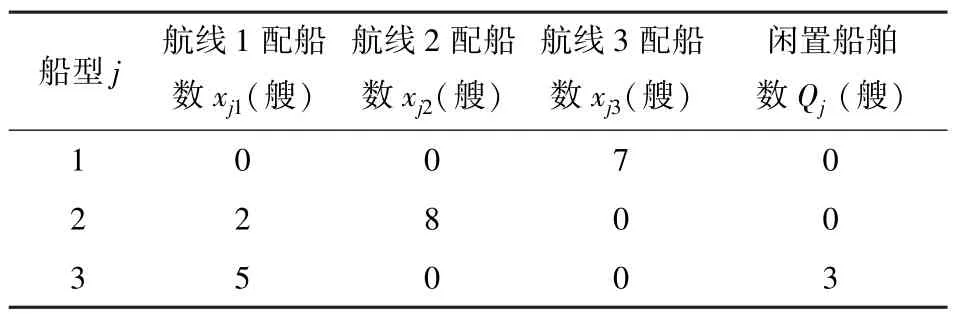
表7 各型船在各航线上采用的航速Table 7 Shipping speed of various types of ships on each route

5 研究结论

全球变暖、环境污染、能源价格上涨成为不可回避的话题,低碳经济越来越受到重视,并已成为应对全球变暖的最佳经济模式.“低碳经济”的发展,将不可避免地对造船、航运及相关配套产业在成本效益、技术、管理等方面带来挑战.本文在传统的班轮航线配船模型的基础上,把航速作为决策变量引入模型中,同时将减少船舶的碳排放量作为优化目标之一,建立了低碳经济下的班轮航线配船模型,并设计了模型的求解方法.通过仿真实验将该模型与传统的航线配船模型的优化结果进行比较分析.结果表明,该模型可以同时决策航线配船和船舶航速,其优化结果更符合实际情况,同时更有利于运力的有效利用,燃油消耗的节省和碳排放的减少.在低碳经济的今天,班轮航线配船也不应再以经营成本最小化或船东盈利最大化作为单一的决策目标,船舶经营者应承担起环境责任,因此航线配船模型的目标函数也应相应的进行调整.但是该模型把研究期定为一年,并且没有考虑到新船的建造、旧船的退役以及船舶的租赁和买卖.此外,航速的降低可能会影响到船东在市场上的竞争力及其市场占有率,进而影响到其船舶的舱位利用率及船公司的利润,将这些因素考虑进去,建立低碳经济下的船队规划模型,并进行优化将会是下一步的研究课题.

[1] Buhaug,J J Corbett,Endresen,et al.Second IMO greenhouse gas study[R].London:International Maritime Organization,2009.

[2] Eurardm.Optimization procedures in maritime fleet management[J].Maritime Policy and Management, 1987(1):27-48.

[3] Perakis A N,Jaramillo D I.Fleet deployment optimization for liner shipping Part1,Background, problem formulation and solution approaches[J]. Maritime Policy and Management,1991,18(3): 183-200.

[4] Jaramill D I,erakis A N.Fleet deployment optimization for liner shipping PartII:Implementation and results[J].Maritime Policy and Management, 1991,18(4):235-262.

[5] Powell B J,Perakis A N.Fleet deployment optimization for liner shipping:An integer programming model [J].Maritime Policy and Management,1997,123 (4):34-35.

[6] Cho S C,Perakis A N.Optimal liner fleet routing strategies[J].Maritime Policy and Management, 1996,23(3):249-259.

[7] 谢新连,李树范,纪卓尚,等.船队规划的线性模型研究与应用[J].中国造船,1989(3):61-68. [XIE X L,LI S F,JI Z S,et al.Application on the linear model of fleet planning[J].Shipbuilding of China,1989(3):61-68.]

[8] 谢新连.船舶调度与船队规划方法[M].北京:人民交通出版社,2000.[XIE X L.Ship scheduling and fleet planning method[M].Beijing:People's Communication Press,2000.]

[9] 杨华龙,钟铭.集装箱班轮航线配船优化决策研究[J].大连海事大学学报,1996,22(3):58-62. [YANG H L,ZHONG M.Studies on optimal decision -making of ship assignment by route in container lines [J].Journal of Dalian Maritime University,1996,22 (3):58-62.][10] 张海健.班轮公司航线配船问题研究[D].杭州:浙江大学,2007.[ZHANG H J.Study on the problem of liner fleet deployment[D].Hangzhou: Zhejiang University,2007.]

[11] 杨秋平,谢新连,苏晨.航线配船与船队规划模型及算法实现[J].大连海事大学学报,2009,35 (1):91-95.[YANG Q P,XIE X L,SU C.Model of ship routing and fleet planning[J].Journal of Dalian Maritime University,2009,35(1):91-95.

[12] 苏绍娟,王丽铮,王呈方.不确定性航线配船数学模型建模方法[J].船海工程,2007,36(4): 100-103.[SU S J,WANG L Z,WANG C F. Mathematical model and method research of ships routing forindeterminateroute[J].Ship&Ocean Engineering,2007,36(4):100-103.]

[13] 李佳,徐奇,殷翔宇,等.基于双目标规划和遗传算法的航线配船优化[J].大连海事大学学报, 2010(4):27-30.[LI J,XU Q,YIN X Y,et al. Optimization of fleet deployment based on bi-objective programming and genetic algorithm[J].Journal of Dalian Maritime University,2010(4):27-30.]

[14] 赵刚.国际航运管理[M].大连:大连海事大学出版,2006.[ZHAOG.Internationalshipping management[M].Dalian:Press of Dalian Maritime University,2006.]

[15] Hughes C.Ship performance:Technical,safety,environmental and commercial aspects[M].London:Lloyd's of London Press,1996.

[16] 王海峰,白佳玉.国际海运温室气体排放的量化分析及中国对策研究[J].海洋环境科学,2010(6): 923-926.[WANG H F,BAI J Y.Research on the quantification of GHG from ships and China's policy response[J].Marine Enviroment Science,2010(6): 923-926.]

Fleet Deployment Model for Liners under Low-carbon Economy and Its Algorithms Implementation

XU Huan,LIU Wei,SHANG Yu-ting
(College of Transport&Communications,Shanghai Maritime University,Shanghai 200135,China)

Considering the nonlinear influence of ship speed on fleet allocation strategy,the paper deduced the mathematical relationship between speed and round-trip time,voyage cost and the number of fleet allocation.It also introduced speed into the model as a decision variable,took the fleet's carbon emission as one of the optimized targets to build a bi-objective(maximum fleet profit and minimize carbon emission) fleet deployment model.Aiming at the nonlinear and mixed integer characteristics of the model,the paper used the self-compiled program and a branch-and-bound algorithm to analyze an example on LINGO11.0 optimization platform.The result shows that the model can develop fleet allocation and speed at the same time.The optimization result can not only further accord with the fact,but also benefit the utilization of the vessel capacity,the save of fuel consumption and the reduce of carbon emission.

waterway transportation;fleet deployment;LINGO;speed;low-carbon economy

F550.81;U692.2+1Document code: A

F550.81;U692.2+1

A

1009-6744(2013)04-0176-06

2013-01-30

2013-04-24录用日期:2013-05-07

国家自然科学基金项目(71272219);上海海事大学研究生创新能力培养专项基金资助项目(YC2010030).

许欢(1981-),女,辽宁锦州人,讲师.

*通讯作者:lovely_xuhuan@163.com