轨道交通模拟驾驶三维视景生成方法

王保山,丁 勇,刘海东

(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044)

轨道交通模拟驾驶三维视景生成方法

王保山*,丁 勇,刘海东

(北京交通大学城市交通复杂系统理论与技术教育部重点实验室,北京100044)

依据模拟驾驶区段的工务数据,在模拟驾驶过程中实时地生成三维视景.根据平面几何和立体几何的基础知识,设计三维空间直线和圆曲线对象的空间走向求解公式,以及以线路中心线为基准的纵断面顶点坐标求解公式.在将坡道、曲线重新组合的基础上,以线段为单位,计算轨道线路中心线的空间走向,根据线路、设备(设施)的纵断面结构,依据线路中心线的空间走向,求解纵断面的顶点坐标,构造三维视景所需要的三维平面要素.同时结合列车的运行状态,确定列车的空间方向,将线路的三维视景经三维平移、旋转得到驾驶场景.使用结果表明,三维虚拟场景能够还原真实场景,帧频率可达25fps,满足真实和实时的要求.

铁路运输;三维视景;三维建模;驾驶模拟;计算机仿真

1 引 言

最近几年,我国的城市轨道交通和高速铁路都在快速发展,模拟驾驶对于司机培训、教学研究都有十分重要的意义,为驾驶员提供真实的虚拟场景是模拟驾驶系统的基本功能.现有的研究成果介绍了三维视景展示所需要的关键技术[1,2],三维视景系统的系统框架和结构[3,4],以及利用三维建模工具创建线路、建筑、列车等三维实体[5,6],通过缩放、旋转再现模拟驾驶区段的三维场景.

本文利用模拟驾驶系统计算列车运行状态所必需的线路坡度、曲线半径等数据,设计线路中心线空间走向求解公式和线路、设备设施外表面顶点坐标求解公式,并用于模拟驾驶三维视景的自动生成.

2 三维视景自动生成的条件

在模拟驾驶路段,线路的坡度、曲线半径、桥梁、隧道等是计算列车运行状态所必需的工务数据.轨道交通线路主要由坡道和曲线组成,线路上有桥梁、隧道、车站,线路的两侧有信号机、里程碑(高架电力线路还有架空输电设备)等,如图1所示.

图1 轨道交通线路组成Fig.1 Composition of rail transit lines

在图1中,坡道根据坡度变化分段给出(l为长度,单位:m,g为坡度,单位:‰);曲线则根据曲线半径的变化分段给出(r为曲线半径,单位: m,0值表示直线);桥、隧、车站等标定的是其中点距线路起始点的距离(用c表示,单位:m)和自身的长度;信号机的位置是按照它与线路起始点的距离标定的.

在轨道交通线路上行驶的机车和车辆都是自动导向设备,线路上直线和曲线部分相连时两者是相切的关系,因此为自动计算线路的空间位置、绘制线路三维视景提供了条件.由于桥、隧、车站的位置是根据线路的位置确定的,所以可以根据线路的位置计算得到.

为三维计算的需要,对组成线路的坡道和曲线进行处理:从线路的起始点开始,沿着线路,在坡度或半径的变化点将线路分段得到若干首尾相连的部分,每一部分称为“线段”,线段的主要属性是长度、半径和坡度.

桥梁、隧道、车站所处位置用相对距离表示:起始点距离模拟驾驶区段起点的距离,终止点距离模拟驾驶区段的起点的距离.为了绘制三维视景,其断面的结构按照与线路中心线的相对位置依次给出,如图2所示.

图2 桥、隧、站房断面示意图Fig.2 Profile of bridge、tunnel and station

在图2中,桥梁、隧道、车站的断面结构简化成折线的形式,折线的顶点P1在水平和竖直方向的偏移分别为w1和h1;P2的偏移为w2和h2;P3的偏移为w3和h3.

3 确定线路空间走向

定义 空间曲(直)线上点P的空间走向是点P的三维坐标和空间曲(直)线在P点的方向组成的四元组,用(xP,yP,zP,εP)表示.定义空间直线上点的方向是它在坐标平面xoz上的投影直线与坐标轴ox的夹角(用弧度表示);空间曲线上点的方向是过该点在坐标平面xoz上的投影点,与空间曲线在坐标平面xoz上的投影曲线相切的切线与坐标轴ox的夹角.

3.1 空间圆曲线空间走向计算

已知AQB为空间圆曲线,曲线半径为r(单位:m,顺时针曲线半径为正值,反时针曲线半径为负值),坡度为gC‰(上坡为正值,下坡为负值,平坡为0值),点A的空间走向为(xA,yA,zA,εA),如图3所示.

图3 空间曲线示意图Fig.3 Sketch map of dimensional curve

空间圆曲线上距离点A为d(m)的任意一点G,它在坐标平面xoz上的投影是点G′,如图4所示.gC的值比较小,一般介于-30和30之间,因此曲线A′Q′B′仍然可以看作半径为r的圆曲线,圆心为C,|AG|≈|A′G′|.

图4 坐标平面xoz上投影曲线和投影点关系Fig.4 Relationship of curve projection and point projection on the coordinate plane of xoz

连接点C和点G′,过点G′作ox的平行线,与过点C平行于oz的直线交于C′,过点A′作ox的平行线,与CC′交于C″,连接点C和点A′.

根据圆心角计算公式有

由于A′C⊥A′A″,且C′C⊥ox,有

根据三角函数公式,有

过点G′在坐标平面xoz上作曲线A′Q′B′的切线G′G″,直线G′G″与坐标轴ox的夹角即曲线AQB在点G的方向,用εG表示,G′C⊥G′G″,且C′C⊥C′G′,所以有

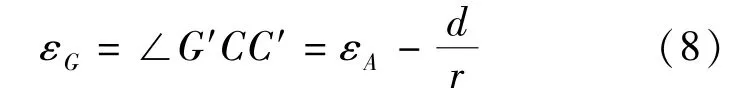
曲线AQB在点G的空间走向用(xG,yG,zG, εG)表示,根据图3和图4中点与线之间的关系,有

所以,根据点A空间走向求解点G空间走向的公式为:

3.2 空间直线空间走向计算

已知空间直线MN坡度为gL‰,方向为εM(弧度),直线MN在点M的空间走向为(xM,yM, zM,εM),如图5所示.

图5 空间直线示意图Fig.5 Sketch map of dimensional line

在空间直线MN上,点K与点M距离为τ (m),直线M′N′是空间直线MN在坐标平面xoz上的投影,点K′是点K在坐标平面xoz上的投影.在坐标平面xoz上,分别过点M′和点K′作坐标轴ox和oz的平行线,由于gL通常较小,所以有|MK|≈|M′K′|,根据三角函数公式,直线MN在点K的空间走向求解公式为

3.3 竖曲线三维坐标计算

两个不同坡度的坡道相连,坡度变化较大时,需要用竖曲线连接,以减少变坡点对列车的冲击,保证运行安全,在变坡点处常利用圆曲线连接两个相邻的坡道.下面以两个直线坡道为例计算竖曲线的空间坐标.

设AB和BD是两个相邻的直线坡道,坡度分别是gAB‰、gBD‰,如图6所示.连接AB和BD竖曲线EMF半径为rC,点E和点F分别是竖曲线EMF与AB和BD的切点.线路中心线AE→EB→BF→FD由AE→EMF→FD替代.

图6 三维竖曲线图示Fig.6 Sketch map of 3D vertical curve

设空间直线AB在点A的空间走向为(xA,yA, zA,εA),直线A′B′和B′D′分别是空间直线AB和BD在坐标平面xoz上的投影,A′、B′、D′三点共线,与坐标轴ox交于点V,则∠D′Vx=εA.竖曲线EMF在空间直线AB和BD所确定的平面上,取AB和BD所在的平面,如图7所示.

图7 竖曲线与轨道中心线平面关系Fig.7 Sketch map of vertical curve and track centerline

设曲线EMF圆心是点C,点A′、E′、B′、F′、D′、C′分别是点A、E、B、F、D、C在坐标平面xoz上的投影,A′、E′、B′、F′、D′、C′6点共线.由于gAB和gBD较小,AB与A′D′的夹角用α表示为

当∠ECF＞0时,令rc取负值;当∠ECF＜0时,令rc取正值.如圆弧半径为20 000 m,当∠ECF＞0时,令rc=-20 000;当∠ECF＜0时,令rc=20 000.

圆弧EMF的长度为

将图7简化,如图8所示.

BD与A′D′的夹角用β表示为

图8 竖曲线平面图解Fig.8 Vertical curve schematic diagram

位于EB上与点E距离l(m)的点Q和点C的连线,与曲线EMF交于Q′,过点E作QC的垂线,垂足为T.

根据式(20),y坐标的修正值为

对于式(22),当点Q在BF上时,l是点Q到点F的距离.

利用式(12)和式(13)的计算结果经过式(21)修正后就得到了竖曲线上点的空间走向.

4 纵断面顶点坐标计算

利用式(12)、式(13)和式(21)可以计算线路中心线的空间走向,根据线路的纵断面结构可以计算组成线路和设备的面的顶点坐标.过线路中心线上点Q与线路中心线垂直的平面截取线路得到如图9所示的断面结构.

图9 线路断面示意图Fig.9 Sketch map of line section

当点Q在曲线上时,为了运行舒适安全,外轨常高于内轨.在线路中心线上,沿线路的方向,设左轨超高υ(m),υ的符号与曲线半径符号相同,在直线段υ=0;轨距为d′(m);点QL相对点Q高度为h(m),点QL在点Q上方时h值为正,在下方时为负;点QL与点Q的相对水平距离μ(m),μ在中心线左侧时为负,在中心线右侧时为正.

过点QL作竖直线与过点Q的水平线交于W,过点Q′L作WQ的垂线,垂足为U.如图10所示.

图10 外轨超高示意图Fig.10 Sketch map of super elevation of outer rail

将坐标平面xoz平移至点Q,点U和点W之间的关系如图11所示.

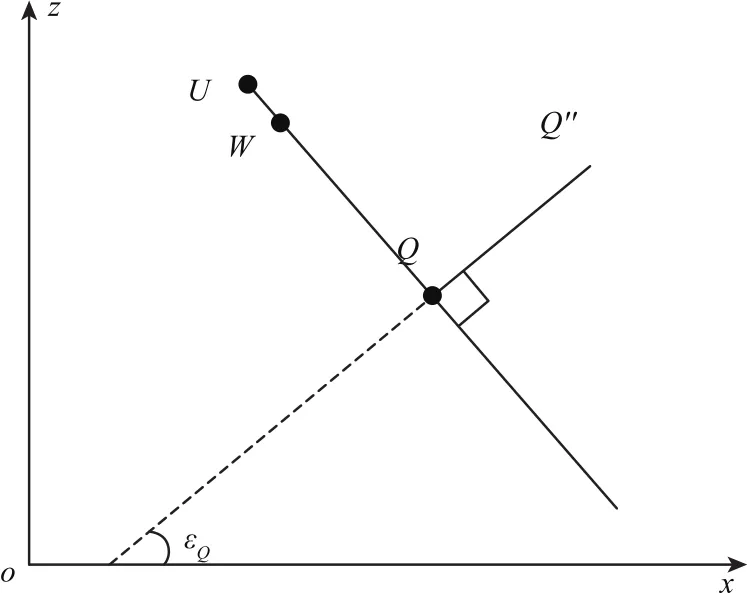
图11 投影点与线路中心线位置关系图Fig.11 Pointprojection and track centerline schematic diagram

点QL在中心线左侧,求解公式为

点QR在中心线右侧,求解公式为

5 模拟驾驶三维视景生成

5.1 模拟驾驶区段线路空间走向确定

设定模拟驾驶区段起点空间走向为(0,0,0, 0),从第1条线段开始,根据起始点的空间走向,曲线半径为0时利用式(13)计算曲线上任意点的空间走向,曲线半径不为0时利用式(12)计算曲线上点的空间走向;并将本线段终止点的空间走向作为其后续线段起点的空间走向.

将第1条线段和第2条线段的交点定为1号交点,并对线路上的交点按增序编号.计算第1个交点处第2条线段和第1条线段的坡度差,当坡度差大于规定值时(如坡度差值的绝对值大于3‰),根据选定的竖曲线半径(如rc=20 000 m)利用式(17)计算竖曲线长度lEMF;根据lEMF确定第1条线段和第2条线段上切点的位置(距离1号交点,利用式(21)修正式(12)或式(13)求得的y坐标作为竖曲线上点的y坐标;按照与第1个交点相同的方式处理所有后续的交点.

5.2 三维视景绘制

沿着线路中心线把线路分成小段(如1 m),每一部分是卧式的柱形结构,根据线路中心线的空间走向和断面结构,计算顶点的坐标,并绘制柱体的表面,得到三维视景.

隧道和站房不受外轨超高因素的影响,利用式(24)和式(25),令υ值为0求解顶点坐标;路基、钢轨、桥面在直线地段没有超高问题,υ取0值计算顶点坐标;路基、钢轨、桥面在曲线上要按照设定的υ值,根据半径的符号给υ设定相应的符号,利用式(24)和式(25)计算顶点坐标.

需要注意的是:在曲线的开始和结尾处要适当修正υ.考虑到车厢的长度约为20 m,所以在进入曲线20 m之内,和在即将离开曲线的最后20 m内,距离切点ζ(m)的地方外轨超高修正为通过修正υ,在从直线进入曲线时,外轨超高从0开始逐步达到最大值;在离开曲线时,也是逐渐减小外轨超高,进入直线时超高为0.

6 实例验证

在模拟驾驶过程中,根据区段内线段的长度、坡度、半径、列车基本阻力、机车牵引特性等,按照一定的时间间隔,依据牵引计算理论计算列车的速度和距模拟驾驶区段起点的距离,根据线段信息计算驾驶室所处的线段,并求得驾驶室距该线段起点的距离,进而计算驾驶室所处点的空间走向(xT, yT,zT,εT),将模拟驾驶区段三维视景平移到(-xT,-yT,-zT),再绕y轴旋转-εT,得到三维驾驶视景.

线路平移、旋转后,在三维坐标系的原点处根据驾驶室高度绘制各种仪表、控制设备等得到驾驶视景.本文利用VC++和OpenGL实现了模拟驾驶三维视景的展示,如图12所示.

图12 模拟驾驶三维视景Fig.12 3D scene driving simulation

驾驶室视景展示的是前方线路和列车运行状态,在图12中,列车处于牵引运行状态,时速约160 km/h,现在列车行驶在顺时针曲线上,线路前方是桥梁,远处是车站,进站信号机显示绿色.

7 研究结论

(1)设计了空间曲(直)线空间走向表达四元组及求解公式、竖曲线y坐标修正公式.利用模拟驾驶区段轨道线路的工务数据计算轨道线路中心线的空间走向,是绘制三维驾驶视景的重要依据.

(2)设计了以线路中心线为基准的外表面顶点坐标求解公式,计算直线和曲线路段及内外轨存在高差情况下的纵断面外表面顶点坐标,是绘制轨道线路、隧道、车站信号机等实体三维视景的基础.

(3)利用模拟驾驶过程中计算列车合力所必需的线路坡度、半径等数据,线路的断面结构,以及隧道、车站等设施的断面结构,通过空间走向求解公式、竖曲线坐标修正公式、以及断面顶点坐标求解公式求解线路、设施的外表面顶点坐标,生成模拟驾驶三维视景,省去了复杂的手工建模工作,具有很强的适应性,可以用于各种复杂路况模拟驾驶视景的自动生成.

(4)将公式应用于模拟驾驶实验系统,能够提供25 fps的三维景象,具有较高的效率.

(5)求解公式可以用于多列车运行仿真、信号布点、线路设计等系统的三维辅助显示.

[1] 程蓉杰,吴芳美.区间测试评估平台的三维交互虚拟场景子系统软件设计[J].铁道学报,2004,26(1): 54-59.[CHENG R J,WU F M.Software design of the interactive 3D virtual scene subsystem of the block testing and assessment platform[J].Journal of the China Railway Society,2004,26(1):54-59.]

[2] 金晓明,茅坪,丁浩,等.基于PC的模拟驾驶视景仿真技术研究[J].系统仿真技术,2008,4(3):167-172.[JIN X M,MAO P,DING H,et al.Scene dimulation in driving system based on PC[J].System Simulation Technology,2008,4(3):167-172.]

[3] 蒋熙,于勇,苗建瑞,等.编组站技术作业过程实时模拟培训系统的研究[J].铁道学报,2001,23(4):7-11.[JIANG X,YU Y,MIAO J R,et al.Study on realtime simulation training system of technological process at marshalling station[J].Journal of the China Railway Society,2001,23(4):7-11.]

[4] 苏虎,周美玉.高速列车模拟器的视景建模与仿真[J].系统仿真学报,2001,13(9):587-591.[SU H, ZHOU M Y.Visual modeling and simulation of the high-speed train simulator[J].Journal of System Simulation,2001,13(9):587-591.]

[5] 史红伟,徐元铭,刘博.基于虚拟现实的列车运行事故再现系统[J].计算机应用,2010,30(2):177-179.[SHI H W,XU Y M,LIU B.Train accident reconstruction system based on virtual reality[J]. Journal ofComputer Application,2010,30(2): 177-179.]

[6] 宋晓伟,唐涛.视景仿真技术在地铁列控系统中的应用[J].北京交通大学学报,2007,31(2):67-71. [SONG X W,TANG T.Application of scene visual simulation in subway trains operation control system [J].Journal of Beijing Jiaotong University,2007,31 (2):67-71. ]

3D Scenery Generation Method for Railway Driving Simulation

WANG Bao-shan,DING Yong,LIU Hai-dong
(MOE Key Laboratory for Urban Transportation Complex Systems Theory and Technology, Beijing Jiaotong University,Beijing 100044,China)

Based on the data of driving simulation section in railway system,three-dimensional(3D)scene is generated in real time during the process of railway simulation.According to the basic knowledge of plane geometry,solid geometry,and the formula of plane geometry,a calculation formula is proposed to solve the spatial location of line and circular curve in 3D space.Another formula is also proposed to calculate the vertex coordinate of vertical section using railway track's centre line as a benchmark.The ramp and curve are recombined and the spatial location of railway track's centre line is then calculated based on the line unit.In view of the vertical section of railway line and facility,the vertex coordinate of vertical section and the required elements of 3D space can be obtained on the basis of spatial location of railway track's centre line.The spatial location of the train is determined considering train running status.Driving scene is obtained after 3D translational motion and rotary motion to railway line.The applications show that 3D virtual display can restore the real scene and the frame frequency is 25 fps,which meets the requirements of the true and real time.

railway transportation;3D scene;3D modeling;driving simulation;computer simulation

U2Document code: A

U2

A

1009-6744(2013)04-0059-07

2013-02-11

2013-04-13录用日期:2013-04-27

国家基础研究计划项目(2012CB725406);国家自然科学基金重点项目(71131001,71231001,70971010);中央高校基本科研业务费专项资金资助项目(2012JBM072).

王保山(1966-),男,山东青州人,讲师,硕士.

*通讯作者:bshwang@bjtu.edu.cn