基于忆阻的自适应单神经元多变量解耦PID控制器

方晓燕，王丽丹，段书凯

(西南大学电子信息工程学院，重庆 400715)

目前，在工业控制中应用最广泛的调节器控制规律为比例、积分、微分控制，即 PID控制［1］。PID控制器问世至今已有近70多年，因其结构简单、稳定性好、工作可靠而成为最常用的工业控制器［2］。随着工业控制中非线性、时变、强耦合、多变量和不稳定等多种复杂控制对象的出现［3］，对PID控制器的参数整定、结构设计、硬件实现、操作手段、适应能力等提出了更高的要求。因此，研究人员提出了基于单神经元、神经网络、模糊［4－6］等的智能控制方法。

1971年，美籍华人科学家 Leon O.Chua教授［7－8］根据电路理论的完备性确定了电荷和磁通量之间的关系，定义了忆阻器，称之为第4种基本电路元件。它是通过控制外加电压(或电流)改变忆阻值实现参数的调整，使其本身可以作为滑动变阻器。同时，忆阻器是纳米级元件具有更微小的体积，而且其本身的类突触特性［9－10］使它可以代替神经网络中的突触权值。

本文利用忆阻器可以作为突触的优势，将此元件应用到PID控制网络中，用忆阻器取代神经网络中3个突触权值，即单神经元网络的比例、积分和微分系数。忆阻突触权值的自动调节使PID控制网络能适应环境的变化，实现多变量控制，满足现代工业对时变、非线性、高控制品质和多变量复杂系统的控制需求，从而可构建基于忆阻的单神经元多变量解耦PID控制器。本文以两变量解耦控制器为例。

1 单神经元自适应多变量解耦PID控制器

随着科技的发展，控制系统变得越来越复杂。其控制量不少于1个，而且所有控制量相互影响。一个变量的变化会引起与其相关的所有变量的变化，这不仅影响系统控制性能，而且影响生产过程的正常运行。为了解决由耦合现象所带来的弊端，需要利用神经网络将耦合的控制系统进行解耦。

为了获得满意的控制效果，研究人员根据多变量控制的理论和实践，提出了多变量解耦控制。解耦的方法为:把多变量耦合系统变成多个独立的单输入单输出控制系统，并利用单变量控制的成熟技术实现多变量系统的设计和控制。

单一的单神经元PID控制器可较好地实现单变量控制。多个单一的单神经元PID控制器构成的网络就可以实现单神经元、多变量PID控制。单神经元PID多变量控制器与单神经元控制器的控制原理是一样的，不同是:单神经元多变量PID控制器是多个输入对应多个输出;单神经元PID控制器是一个输入对应一个输出。本文的单神经元自适应多变量解耦PID控制器选择单神经元自适应两变量解耦PID控制器，其结构如图1所示。

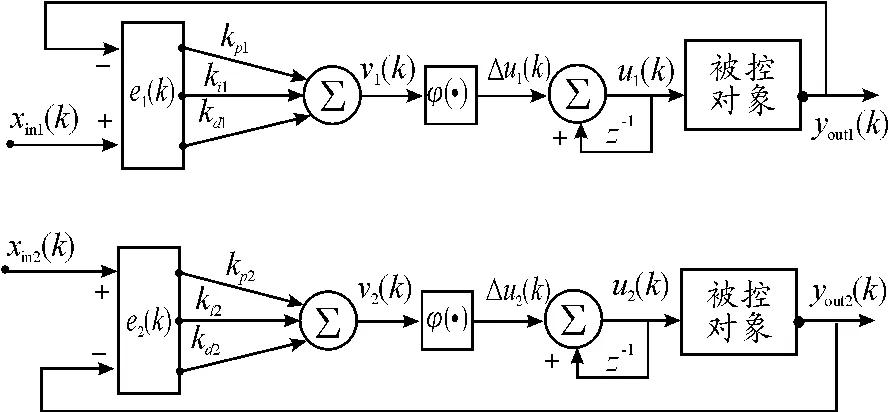
图1 单神经元自适应两变量解耦PID控制网络结构

单神经元两变量解耦PID控制器的工作原理和单神经元PID控制器的工作原理完全相同，只是输入变为2个:xin1(k)和xin2(k)，输出变量变为2个:yout1(k)和yout2(k)。

2 基于忆阻的单神经元自适应两变量解耦PID控制器

根据单神经元两变量解耦PID控制器的结构和忆阻器可以替代神经突触的特性，用忆阻器替代单神经元两变量PID控制网络中的突触权值，得到基于忆阻的单神经元两变量解耦PID控制网络结构，如图2所示。

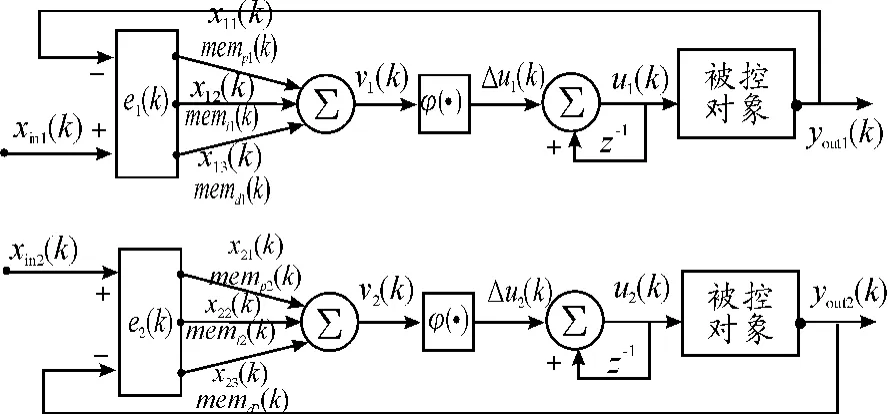
图2 基于忆阻的单神经元自适应两变量解耦PID控制网络结构

基于忆阻的单神经元自适应两变量解耦PID控制网络的真正输入是误差信号e1(k)和e2(k)，表达式分别为:e1(k)=xin1(k)－yout1(k);e2(k)=xin2(k)－yout2(k)。2个误差信号同时输入到网络中，PID控制网络进行并行处理，2个单神经元PID控制器分别根据某学习规则，使突触权值不断进行学习修正，直到2个PID控制器的误差都为零为止。

本文用忆阻器替代PID网络中的比例、积分和微分系数，得到基于忆阻的PID两变量控制器的突触权值表达式:

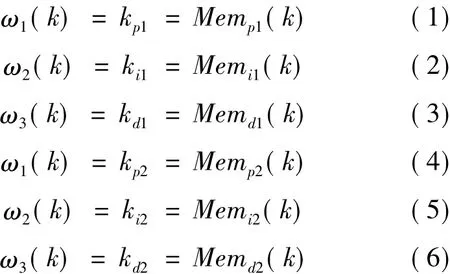
基于忆阻的PID两变量控制器的输入状态量分别为:

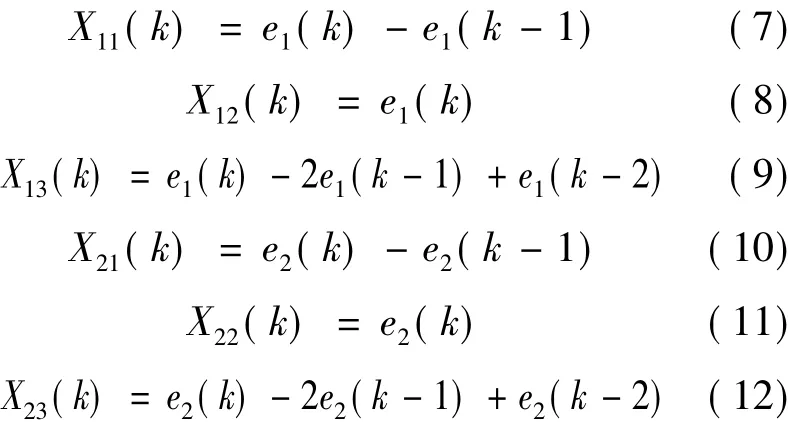
输出作用律表达式分别为:

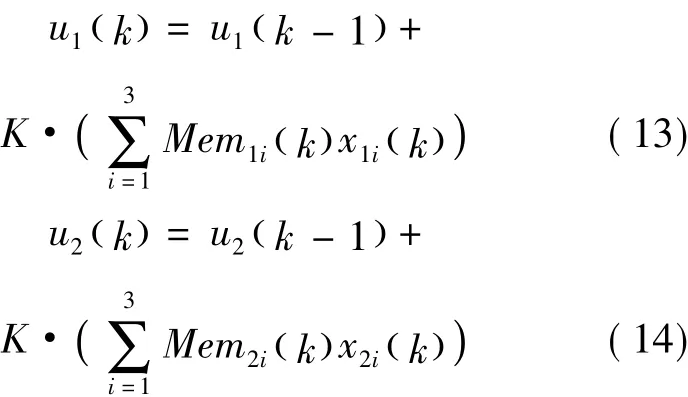
其中φ(·)是基于忆阻的单神经元自适应两变量解耦PID控制网络的激活函数，这里为神经元比例系数K，且为正实数，取值范围为K∈(0，1)。

3 忆阻感知器不同学习规则下的基于忆阻的单神经元自适应两变量解耦PID控制器的Matlab仿真

本文给定的输入为单位阶跃输入，即xin1(k)=1，xin2(k)=0。PID控制器中2个变量的被控对象分别为:

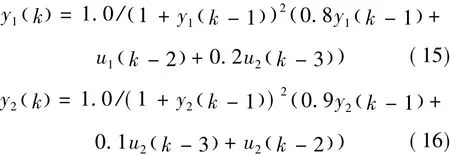
输入信号的初始值分别为:x11=0，x12=0，x13=0，x21=0，x22=0，x23=0;2个PID网络的学习效率为:αp=0，αi=0，αd=0;2个 PID 网络的突触权值的初始值分别为:Memp1=0.1，Memi1=1.1，Memd1=1.6;Memp2=0.01，Memi2=0.006，Memd2=0.005，采样时间为 0.001s。

根据权值修正公式，得到不同规则下的位置跟踪曲线(见图3～6，其中虚线为输入阶跃信号xin1=1和xin2=0，光滑实线是输出曲线yout1，实线是输出曲线yout2)。

在无监督的Hebb学习规则下，基于忆阻的单神经元两变量解耦PID控制器的突触权重的修正公式为:在有监督的Hebb学习规则下，基于忆阻的单神经元两变量解耦PID控制器的突触权重的修正公式为:

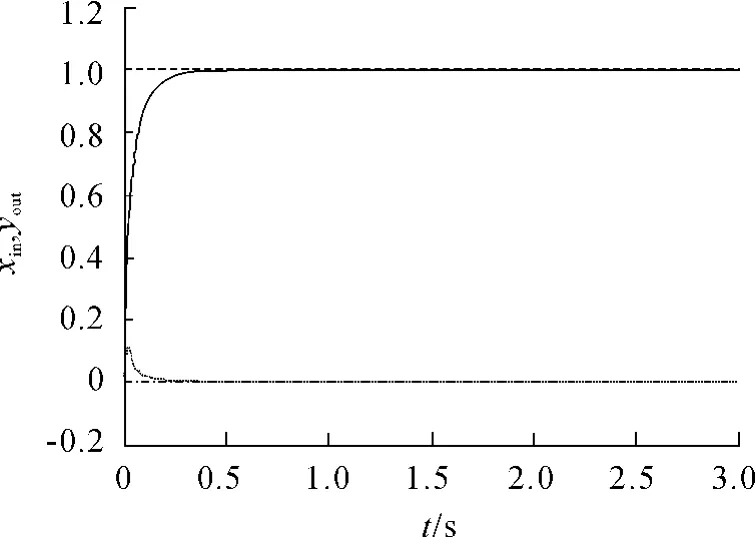
图3 无监督的Hebb学习规则下的位置跟踪曲线

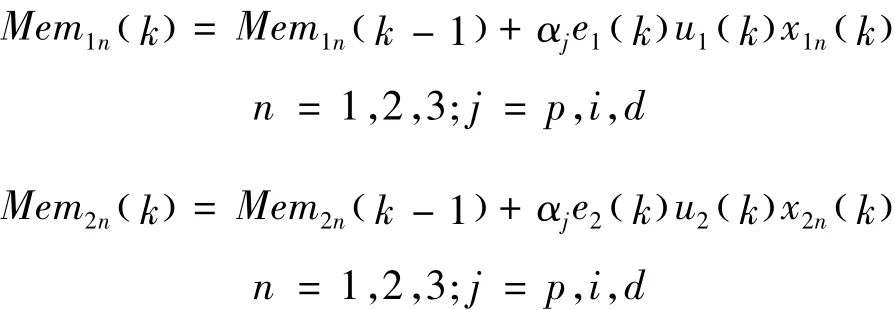
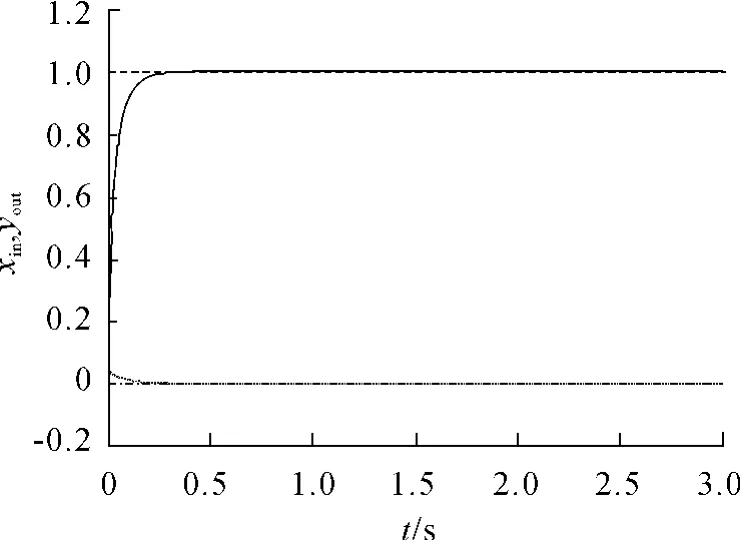
图4 有监督的Hebb学习规则下的位置跟踪曲线

在LMS学习规则下，基于忆阻的单神经元两变量解耦PID控制器突触权重的修正公式为:

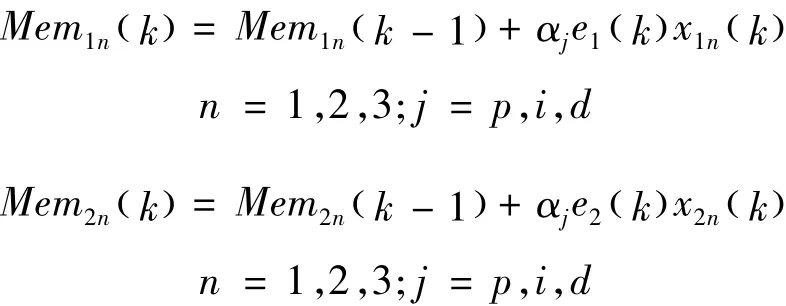
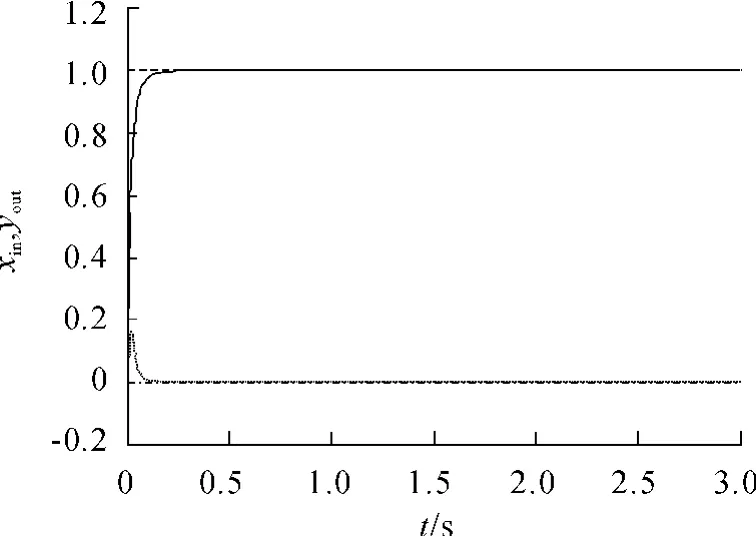
图5 LMS学习规则的位置跟踪曲线

改进的基于忆阻的单神经元两变量解耦PID控制器的突触权重的修正公式为:

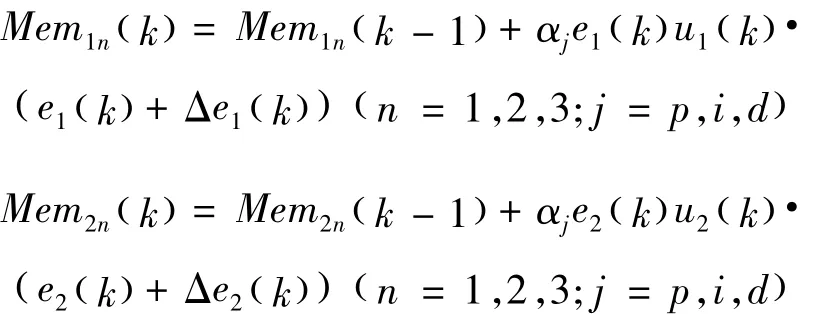
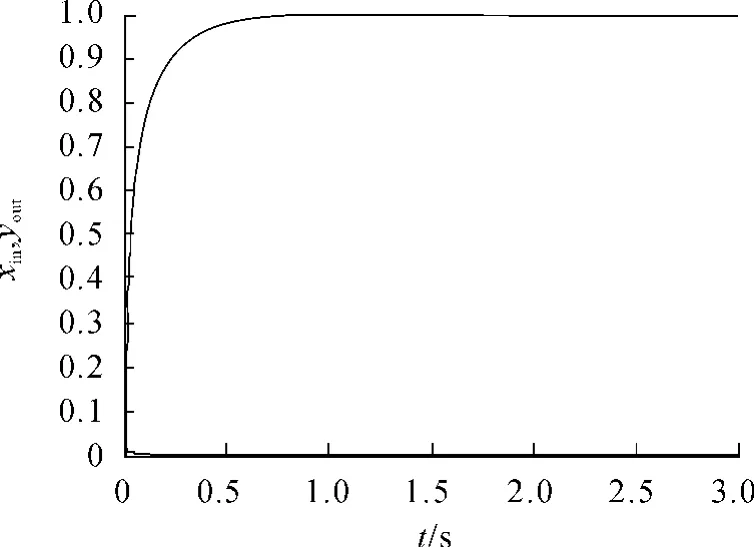
图6 改进的学习规则的位置跟踪曲线

4 基于忆阻的单神经元两变量解耦PID控制器与单神经元两变量解耦PID控制器的比较

在相同的初始值、相同的学习规则下，将基于忆阻的单神经元两变量解耦PID控制器与单神经元两变量解耦PID控制器的输入输出跟踪曲线和误差曲线分别进行分析比较，其曲线见图7、8(两控制器输入分别为1和0，都为蓝色线;黑色、红色曲线分别是在控制器输入为1时基于忆阻PID控制器和PID控制器的输出曲线;品红色、绿色曲线分别是在控制器输入为1时基于忆阻PID控制器和PID控制器的输出曲线)。

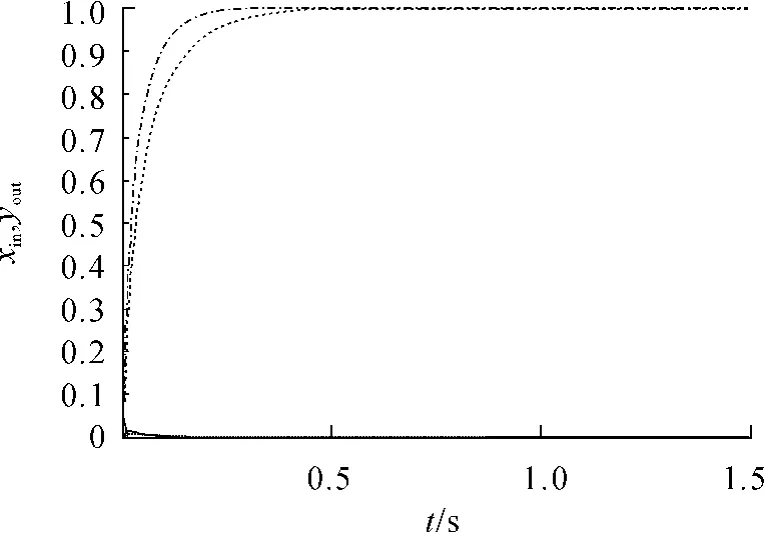
图7 2个PID控制器的输入输出跟踪曲线

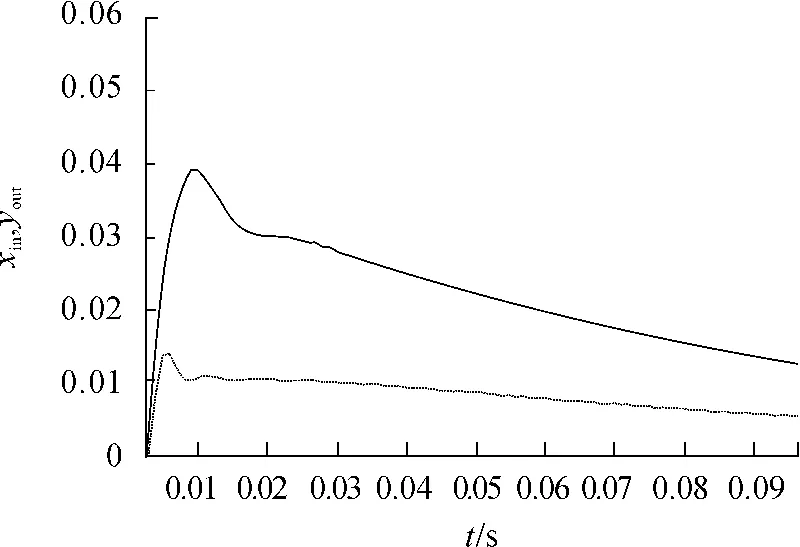
图8 放大后的PID控制器的输入输出跟踪曲线，输入信号为xin(k)=0

从以上2个PID控制器的输入、输出曲线(图7、图8)，可以观察到基于忆阻PID控制器(绿色)与PID控制器的输出跟踪曲线(品红)相比，前者上升时间(输入信号为xin(k)=1的情况下)和下降时间变短(输入信号为xin(k)=0的情况下)，超调量变小，使整个系统的学习速度快，曲线拟合效果好，系统稳定，达到较好的自适应控制效果。

5 基于忆阻的单神经元两变量解耦PID控制器的应用

倒立摆系统是一个典型的非线性、强耦合、多变量和不稳定系统。本文以一阶倒立摆作为PID控制系统的被控对象，系统的2个输入信号分别为阶跃信号xin(k)=1和xin(k)=0，被控对象分别为倒立摆摆杆角度和小车位置。因此，构成了两输入两输出的两变量控制系统。

摆杆角度的传递函数为

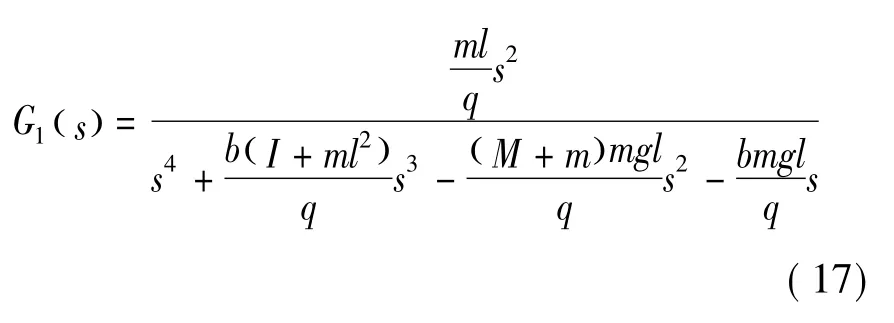
小车位置的传递函数为

其中:M是小车质量;m是摆杆质量;b是小车摩擦因数;l为摆杆转动轴心到杆质心的长度;I为摆杆惯量;ts为采样时间。以上参数的取值分别是:b=0.1，M=0.5，m=0.2，g=9.8，I=0.006，ι=0.3，ts=0.001，q=(M+m)·(I+mι2)－ (mι)2。

从图9可观察到，系统的2个响应曲线跟踪效果较好，而且摆杆角度跟踪曲线超调比较小，整个系统的控制比较理想。

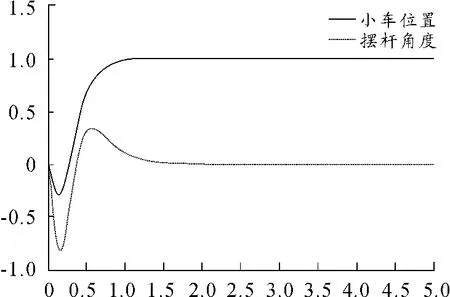
图9 小车位置和摆杆角度跟踪曲线

6 结束语

本文从理论阐述和仿真实验2个方面对基于忆阻的单神经元多变量解耦PID控制器进行了分析。此系统不仅可以实现较好的跟踪控制，而且误差和超调量都比较小，权值学习修正速度较快，符合控制要求。由于忆阻器是纳米级器件，所以有可能实现体积小、功耗低、精度高、功能强的超大规模集成(VLSI)电路和微控制器。本控制系统经过解耦设计后，整个控制系统振荡明显降低，且具有自适应能力强、响应速度快、两变量控制效果好和抗干扰能力强等特点。基于忆阻的单神经元多变量解耦PID控制器的实现为基于忆阻的多输入多输出的单神经元多变量解耦PID控制器的实现和应用奠定了基础。

［1］Yin Y H.The Intelligent PID control of filature production line slack-loop system［C］//2011 The 6th International Forum on Strategic Technology.Harbin:［s.n.］，2011:378－381.

［2］Bennett Stuart.A history of control engineering，1930 －1955［M］.［S.l.］:The Institution of Engineering and Technology(IET)，1993.

［3］Chen J，Cheng N，Zhang J.Neural based PID control for networked processes［C］//Proceedings of the 2011 4th International Symposium on Advanced Control of Industrial Processes.Hangzhou:［s.n.］，2011:466 －471.

［4］Chen X X，Wang C G，Wu H Z.PID:Controllers Parameters Self-tuning algorithm based on frequency characteristic［C］//2010 International Conference on Measuring Technology and Mechatronics Automation.Changsha:［s.n.］，2010:891 －894.

［5］Zhang Y H，Zhao D.Research on PID Controller Based on the BP Neural Network［C］//2011 International Conference on Electronic＆Mechanical Engineering and Information Technology.Harbin:IEEE，2011:516 －519.

［6］Guangjun Yang，Bing Xiao，Xiaojuan Zhu.A Method of Neuron PID Control Based on Fuzzy Regulating Gain［J］.Automatic Control and Meter，2004，19:44 －46.

［7］Chua L O.Memristor－ The Missing Circuit Element［J］.IEEE Transactions on Circuit Theory，1971:507－519.

［8］Chua L O.Device Modeling via Nonlinear Circuit Elements［J］.IEEE Transactions on Circuits and Systems，1980，27:1014 －1044.

［9］Sharifi M J，Banadaki Y M.General Spice Models for Memristor and Application to Circuit Simulation of Memristor-Based Synapses and Memory Cells［J］.Journal of Circuits，Systems，and Computers(JCSC)，2010，19:407－424.

［10］Corinto F，Ascoli A，Gilli M.Memristive Based Oscillatory Associative and Dynamic Memories［C］//Cellular Nanoscale Networks and Their Applications(CNNA)，2010 12th International Workshop on，2010:1 －6.