Logit随机网络配流模型的改进Dial算法
2013-07-31严余松户佐安
杨 泳,严余松,户佐安,马 毅
(西南交通大学交通运输与物流学院,成都610031)
Logit随机网络配流模型的改进Dial算法
杨 泳,严余松*,户佐安,马 毅
(西南交通大学交通运输与物流学院,成都610031)
研究Logit随机网络配流模型及实现模型求解的Dial算法,针对原模型及算法的缺陷,通过引入路段长度相关的容错系数指标重新定义有效路径的判定条件,在此基础上提出一种改进的Dial算法,并应用于Logit随机网络配流模型中.改进算法在不降低原算法精度下不仅保留了原算法的无需路径枚举、计算效率高等优越性,而且满足实际出行者偏好在较短路段上“迂回”选择潜在有效路段的特点.最后通过一个路网实例对2种算法的配流结果进行了对比.结果表明,改进的算法避免了原算法缺陷导致的结果异常,配流效果更加符合实际,其计算效果明显优于原算法.
城市交通;配流;有效路段;Logit模型;Dial算法;交通网络;容错系数
1 引 言
给定交通需求与路网供给特征,求解网络流量分布的交通问题被称为配流问题.每个出行者总是力图选择起讫点之间阻抗最小的路径,当不存在出行者能单方面改变出行路径从而降低阻抗时,达到一种稳定状态,被称为用户平衡状态(UE)[1].在用户平衡配流中,假定用户知道每条可选路径的准确交通时间,而且能够持续做出完全正确的路径选择决策.在此假设前提下,形成的交通流平衡状态称为确定性用户平衡[2].然而该假设是不合理的,由于客观信息的缺乏和主观路径的偏好,对于同一路径,不同用户估计的交通时间不同.将用户对路段阻抗的理解值与实际值之间的差别视为随机变量,出行者会选择自己认为阻抗最小的路径而达到一种平衡状态,被称为随机用户均衡状态,把这种条件下的流量分配也称为随机性配流[1,2].
在随机性配流问题中,路径集的选取相当重要,因为路径集的定义不同,选择路径的行为准则和概率则不同,将直接影响配流的效果.Dial于1971年提出的STOCH算法[3]是求解非拥挤交通网络随机配流问题的经典算法之一,该算法以路段为媒介,无需路径列举,配流结果满足多项式Logit模式,适用于大规模交通网络,也称Dial算法.该算法有识别有效路径的初始化阶段,许多明显不被出行者考虑的路径被隔离在有效路径集之外,OD流量仅限在有效路径集上进行分配.但由于Dial算法对有效路径集的选取过于严格,导致出现阻抗较低的路径未被使用而阻抗较高的路径反被使用的异常现象,配流结果明显不满足Wardrop第一与第二原则[1],从而限制了 Dial算法在实际中的应用.
针对Dial算法实际应用中存在的局限,各国研究者设计了一些改进的模型和算法.Bell[4]、BAR-GERAH[5-7]提出了相关的Logit改进模型及改进Dial算法,通过网络权重矩阵的求和序列及矩阵变换来计算Logit模型,但对于求解大规模交通网络缺乏有效的算法;李景等[8,9]针对有效路段和有效路径两个概念对多路径分配问题进行了深入的研究及模型的改进;李志纯等[10,11]分别从广度优先和深度优先2个方向给出了求解网络中2个节点间所有连通路径的算法,这2种搜索方法的时间复杂度相同,只是对节点的访问顺序不同;李军等[12]基于拓扑排序的思想提出寻找路径的算法,但只有在网络存在环路的情况下才可以排除不合理路段,这个假定条件对于实际的交通网络而言并不合理.这些方法多基于图论的有效路径算法或连通路径算法,在求解实际问题时存在一定的困难.
本文在研究随机交通流分配中有效路径选择的基础上,提出一种改进Dial算法.在新算法中放宽对有效路径的定义,选取有效路段时考虑该路段实际阻抗,避免原算法所产生的错误的同时,合理解释实际交通过程中出行者的路径选择行为,使交通流分配结果更符合实际情况.
2 Logit模型及Dial算法
在随机性配流问题中,定义起讫点r,s间各备选路径具有令人满意的程度为效用,出行者总是选择主观判断效用最大的路径,第k条路径的效用值可表示为
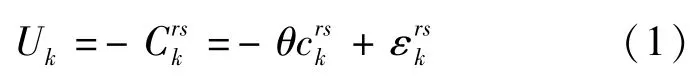
式中 Uk为起迄点选择路径k的效用;crks为路径k的实测阻抗;θ为将一个实测阻抗转换成效用的正的转换参数;εrks表示路径不能观测到的因素构成的随机误差项.Logit模型就是建立在随机误差项相互独立且服从Gumbel分布的基础上[13],基于Logit模型的求解选择路径k的概率为

这样通过各路段的选择概率Prks,就可以得到各路径上的流量

式中 qrs为r,s之间的交通需求量.当含有n个节点完全图中,任意两个节点之间的路径数为其中Pi=n!/i! .在实际交通网络中,
n虽然节点的邻接边比较少,但要找出r,s间所有的路径进行计算也是不切实际的.
Dial算法定义OD对r,s之间的路径上任意满足下列条件的路段i,j为有效路径
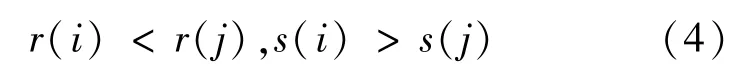
式中 r(·)为相应节点到起点r最小路径阻抗; s(·)为相应节点到终点s的最小路径阻抗.
Dial算法的具体执行步骤如下[1].
步骤1 初始化.对路网中每一个节点,采用最短路径算法求解 r(i),s(i).最短路径算法有Dijkstra算法、Floyd-Warshall算法和Moore-pape算法等,本文计算采用Floyd-Warshall算法.
步骤2 计算路段似然值.对每条路段i,j,计算各有效路段的似然值
式中 cij为路段i,j的实际阻抗值.
步骤3 向前计算路段权重.从起点r开始,按r(i)的上升顺序依次考虑节点,对于每个节点,计算离开它的所有路段的权重值W值.W(i,j)的计算公式为

式中 Ii为终点为i的路段起点集合,当达到终点s时终止计算.
步骤4 向后计算路段流量.从终点s开始,按s(j)的上升顺序依次考虑节点,对每个节点,计算进入它的所有路段的流量X,计算公式为

式中 qrs为OD对r,s之间的交通需求量;Oi为起点为i的路段终点集合,当达到起点r时终止计算.
3 有效路段的重新定义
1971年Dial提出的算法能较好地实现Logit模型的求解过程,其出发点是通过判断一条路径是否为“有效路径”来排除大量的“无效路径”.由于Dial算法对有效路径的定义过于严格,将导致分配结果中阻抗较低的路径不被使用,而阻抗较高的路径反被使用的现象.
如图1的算例网络中,共有9个节点,13条路段,弧段上方或右侧数字代表该路段的时间阻抗.起点1到讫点9的OD分布量q1,9=1 000个单位出行量,根据Logit模型及相应的Dial算法对该道路网络进行流量分配,结果如图2所示.

图1 道路网络图Fig.1 Example for road network

图2 Dial算法的配流结果Fig.2 Assignment result with Dial's algorithm
从配流结果图2可以看出,路段7-8并没有得到流量分配.表1列出Dial算法初始化后响应节点到起点1的最小阻抗值,根据Dial算法对有效路段的定义,可以发现路段(7,8)并不属于有效路段,所以1-4-7-8-9就被排除在配流的有效路径之外.然而1-4-7-8-9的阻抗为8,而被认为有效路径的1-2-3-6-9阻抗也为8,显然,这结果是不合理的.

表1 Dial算法的初始化Table 1 Initialization of Dial's algorithm
在实际的交通网络中,出行者在进行路径选择过程中,通常不会严格遵守Dial定义的“离起点越来越远,离终点越来越近”有效路段条件,而在可预见范围内能容忍一定程度的偏差.这种偏差易引起出行者在选择有效路段时与Dial严格定义的有效路段形成一定的误差,实际上选择一些在严格意义上的非有效路段而“迂回”前进,从而达到不断靠近终点的出行目的.这些额外被考虑的“有效路段”,其费用通常可以预见且在出行者可承受范围之内.受这一现象的启发,本文通过引进基于路段量化指标Δ(i,j)——容错系数.对此,可重新定义有效路段为,如果OD对r,s之间路段i,j满足下列条件,则该路段为有效路段

从式(8)可以看出,有效路段的判断准则根据出行者的实际出行行为进行优化,从而达到对有效路段进行有效控制和扩展的目的.在实际的路网中,按照这种方法确定有效路段集会随出行者对路网的熟悉程度及风险偏好程度的变化而发生变化,因而引入容错系数上线来定量描述路网中出行者实际出行条件下对不满足“离起点越来越远,离终点越来越近”的量化容忍程度,且分别用定义出发点、终止点的容错系数,两者相互独立.容错系数上限越高,说明出行者越偏好在路网中“迂回”选择有效路段,而且对于相同容错系数上限而言,路段越长,出行者越容易考虑其相连通且路段长度较短的支路.在的情况下,式(4)和式(8)等价,即原始有效路段判定条件是假定出行者完全掌握路网信息且不能容忍任何非有效路段介入的特殊情况.
在原始的Dial算法中,计算节点序列与有效路段的判定是密切相关的.根据有效路段的重新定义后,依然可以采用原始算法的执行步骤,保留算法无需穷举所有连通路径的优点,因此改进后的Dial算法在步骤2计算路段似然值时更新如下
步骤2(更新) 计算路段似然值.对每条路段i,j,计算各有效路段的似然值

4 算例分析
以图1算例网络为例进一步说明改进后的模型流量分配结果,取详细计算结果如表2所示.
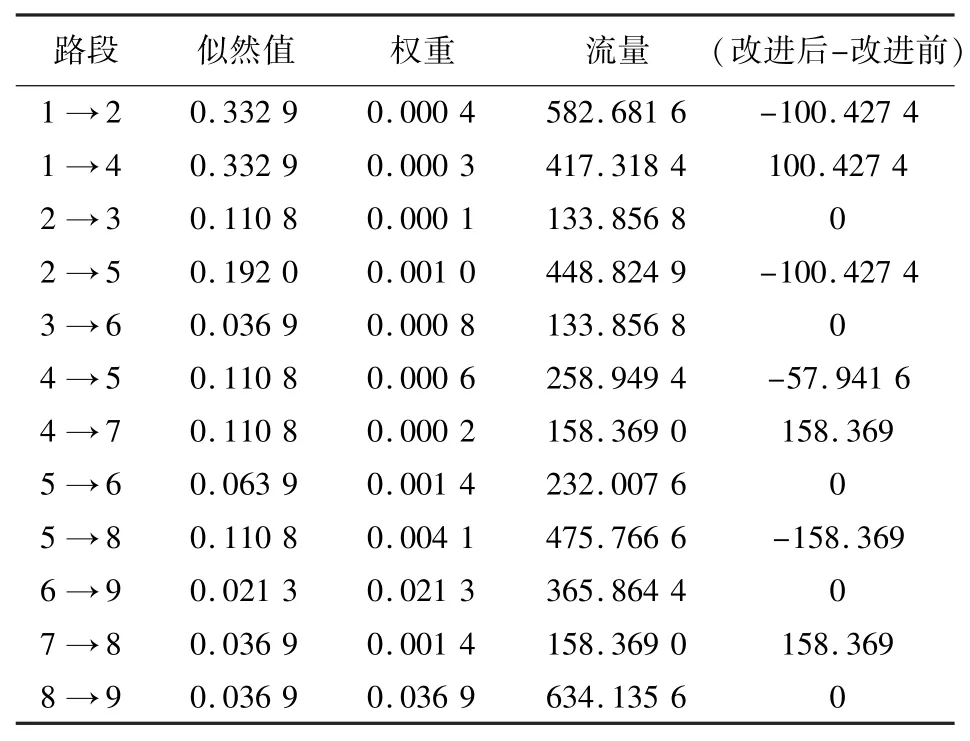
表2 算法改进前后配流结果对比Table 2 The assignment result comparison between before improvement and after improvement
图3为网络中基于改进的有效路段判定条件下的配流结果,对比图2可以明显看出,路径4-7-8从零流量的不合理情况得到一定的流量分配,解决了一些本应被选择的有效路径没有分配到交通量的不合理配流现象.
图4显示算法改进前后流出节点流量的结果对比,横坐标表示道路网络图1中对应的节点序号,纵坐标表示节点流出的流量,可以明显看出,随着新的有效节点7的流量分流,网络中大部分节点的流量保持不变或者有所降低,整个网络流量分配趋于均匀合理化,而在流量减少的节点中,以交通最为拥挤的中心节点5下降最为明显,降幅高达18.3%,说明正确的交通流分配模型及算法对于合理分配路网流量特别是交通量非常高的中心路段的分流作用是非常明显的.而对于节点4,流出流量有一定程度的上升,原因是节点4连通中心节点5及新的有效节点7,但其流量总量(417.3)相比于中心节点5不大,有利于提升节点4的路网使用效率.根据改进Dial算法,可以确保一部分非严格意义上的有效路段也得到一定的流量分配,得到比原始Dial算法更符合世纪的配流结果.

图3 改进Dial算法的配流结果Fig.3 Assignment result with improved Dial's algorithm

图4 算法改进前后节点流量对比Fig.4 The node flow assignment comparison between before improvement and after improvement
5 研究结论
本文针对Logit模型的Dial算法固有缺陷,提出一种基于路段阻抗的容错系数对有效路段重新定义,并在路网中验证改进模型和算法.研究结果表明:
(1)改进Dial算法保留了原Dial算法的优点,即在配流过程中,不需要列举所有连通路径,而是通过路段信息进行有效路段的筛选;
(2)对有效路段进行了重新定义,与原Dial算法相比,改进Dial算法可得出更加合理的有效路段集合,从而避免了原Dial算法遗漏有效路段的内在缺陷,使配流结果更加合理;
(3)在改进Dial算法中,影响有效路径集合的因素主要是出行者在路段预见范围内对偏差容忍程度,即路段容错系数Δ(i,j),系数越大,说明出行者越偏好在路网中“迂回”选择有效路段,在零容错条件下模型与原模型等价;
(4)改进的Dial算法在考虑路段的容错能力时,仅考虑了本路段的阻抗,并没有考虑其相邻路段的阻抗;然而,在出行者实际交通选择过程中,不仅仅考虑本路段的状况,还将考虑相邻路段的情况,因此如何在“有限”范围内考虑相邻路段的实际情况来进一步研究有效路段的选择,有待做进一步的研究.
[1]Sheffiy.Urban transportation networks equilibrium analysis with mathematicalprogramming methods [M]. Englewood Cliffs New Jersey:Prentice Hall,1985.
[2]Sheffiy.城市交通网络[M].云辉,戴香菊,译.成都:西南交通大学出版社,1992.[Sheffiy.Urban transportation networks[M].YUN H,DAI X J, Translate.Chengdu:Southwest Jiao Tong University Press,1992.
[3]Dial R B,A probabilistic multipath traffic assignment model which obviates path enumeration[J]. Transportation Research,1971,5(2):83-111.
[4]Bell M G H.Alternatives to Dial's Logit assignment algorithm[J].Transportation Research Part B,1995, 29(4):287-295.
[5]Bar-Gera H.Primal method for determining the most likely route flowsin large road networks[J]. Transportation Science,2006,40(3):269-286.
[6]Larsson T,Lundgren J T,Patriksson M,et al.Most likely traffic equilibrium route flows:analysis and computation[M].Netherlands:Kluwer Academic Publishers,2001:129-159.
[7]Bar-Gerah Luzonal.Differences among route flow solutions for the user equilibrium origin-based algorithm for the traffic assignment problem[J]. Journal of Transportation Engineering,2007,133(4): 232-239.
[8]李景,彭国雄,臧亦文.改进型多路径分配模型及算法设计[J].系统工程理论与实践,2001(9): 130-134.[LI J,PENG G X,ZANG Y W.An improved multi-path assignment model and algorithms design[J].Systems Engineering-Theory&Practice, 2001(9):130-134.]
[9]郭仁拥,黄海军.考虑OD需求变异的网络交通流演化模型[J].系统工程理论与实践,2009(1): 118-123.[GUO R Y,HUANG H J.Network traffic flow evolution model considering OD demand mutation [J].Systems Engineering-Theory&Practice,2009 (1):118-123.]
[10]李志纯,黄海军.随机交通分配中有效路径的确定方法[J].交通运输系统工程与信息,2003,3(1): 28-32.[LI Z C,HUANG H J.Determining the efficient paths in stochastic traffic assignment[J]. Journal of Transportation Systems Engineering and Information Technology,2003,3(1):28-32.]
[11]朱顺应,王炜,邓卫.交通网络可靠度及其通路算法研究[J].中国公路学报,2000,13(1):91-94. [ZHU S Y,WANG W,DENG W.Research on traffic network reliability and access road algorithm[J]. China Journal of Highway and Transport,2000,13 (1):91-94.]
[12]李军,辛松歆,蔡铭.基于拓扑处理的Logit型网络加载算法[J].中国公路学报,2005,18(4):87-90.[LI J,XIN S X,CAI M.Algorithm for Logit network loading problem based on topological sorting [J].China Journal of Highway and Transport,2005, 18(4):87-90.]
[13]黄海军.城市交通网络平衡分析-理论与实践[M].北京:人民交通出版社,1994.[HUANG H J. Urban transportation network equilibrium analysis: theory and practice [M]. Beijing: China Communications Press,1994.]
Improved Dial's Algorithm for Logit-Based Stochastic Traffic Assignment Model
YANG Yong,YAN Yu-song,HU Zuo-an,MA Yi
(School of Transportation and Logistics,Southwest Jiaotong University,Chengdu 610031,China)
This paper analyzes the multi-path Logit assignment model and the classical Dial's algorithm. To overcome the drawback in existing model and algorithm,an improved algorithm is presented.The efficient path condition is modified based on a quantitative correction coefficient on individual path.The improved algorithm retains the main advantages of original algorithm,in which the path enumeration is not required and a similar computing efficiency with the original algorithm is guaranteed.Meanwhile,the preference to potential valid road links with short distance among urban traffic travellers is satisfied.A numerical example based on a traffic road network is used to illustrate the application of proposed algorithm and two algorithms are then compared.Results show that the improved algorithm is able to eliminate the abnormal behavior of the original algorithm with more feasible and reasonable traffic flow assignment results.It is evident that the proposed algorithm is more effective than the original one.
urban traffic;traffic flow assignment;effective path;Logit model;Dial's algorithm;traffic network;correction coefficient
TP18,U491
A
TP18,U491
A
1009-6744(2013)02-0158-06
2012-10-30
2013-01-25录用日期:2013-02-05
国家自然科学基金(61104175).
杨泳(1982-),男,湖北大治人,博士生.
*通讯作者:yanyusong@263.net
