首都机场航班延误分布规律分析

杨文东,黄鹂诗,刘万明,2

(1.南京航空航天大学民航学院南京210016;2.中国民用航空局运输司北京100710)

首都机场航班延误分布规律分析

杨文东*1,黄鹂诗1,刘万明1,2

(1.南京航空航天大学民航学院南京210016;2.中国民用航空局运输司北京100710)

近年来航班延误现象愈演愈烈,严重影响旅客、机场和航空公司的利益.受天气、管制、人为因素的影响,难以彻底消除航班延误,但可以探究航班延误的内在原因及其发展规律,减少或避免不必要的损失.通过对首都机场的追踪统计,分析不同航空公司、不同时段的延误时长、延误率和延误波动;建立一天延误时长分布的核概率密度函数,证明在以往机场仿真时将延误时长分布看作是正态分布并不合理;提出直接利用延误总时长拟合最佳窗宽的方法.结果表明,该方法精度达到航班延误规律分析要求,可以为不正常航班情形下的运行调度和恢复提供参考.

航空运输;航班延误;延误时长分布;核概率密度函数

1 引 言

民航业的快速发展,使我国空域日趋拥挤、机场更加繁忙.近年来航班延误现象愈演愈烈,严重影响了机场、航空公司和旅客的利益,广大旅客对出行延误反映强烈.中国民用航空局出台了一系列措施,努力减少航班延误,但延误现象还是时有发生.一个机场的延误程度究竟如何,不同航空公司、不同时段的延误情况需要定量的数据进行刻画,同时也是进一步采取改进措施的基础.

目前国内外对航班延误分析较多,部分文献从定性角度和处治措施方面进行了一定程度的研究[1-3];部分文献从航班延误的波及关系出发,提出了航班延误链式反应波及的机场个数与飞机的初始延误时间[4-9];也有文献对航空公司的延误成本结构进行了分析,提出了测算航班延误成本分析模型[10].上述研究对机场航班延误的统计规律有所忽略,未给出机场航班延误时长的仿真建议.机场仿真一般是以航班时刻表进行驱动,或采用计划航班时刻表,或认为航班延误时长为正态分布,或用每次调查数据作为输入参数,但对新建机场进行系统容量和优化仿真时,无法获得实际数据直接影响分析的科学性,为此本文选取首都机场的航班情况进行延误分析,探究延误现象的具体表现和内在规律.

2 航班延误调查

此次调查以一个星期为周期,记录每日航班的计划离港时间和实际离港时间,分析航班延误情况.调查期间周六遇到下雪天气,航班延误情况比较严重,属于特殊情况.被调查机场共有15家航空公司,其中基地航空公司4家,分别是A、B、C、D.各航空公司每日航班数如表1所示,I～O航空公司每日航班数不超过10个班次,基地航空公司中尤以A公司航班最多.

(1)延误总时长分析.

按照规定延误超过15 min的航班作为延误航班,各航空公司每日航班的延误总时长如表2所示.周六由于受天气影响,机场航班延误总时长超过了平时的2倍,达36 020 min.除去周六,机场延误总时长一般在13 712～18 843 min之间,每个航班平均延误时间在37～45 min之间,表明航班延误出现的几率基本相近,每日延误航班数处于一个稳定的水平.

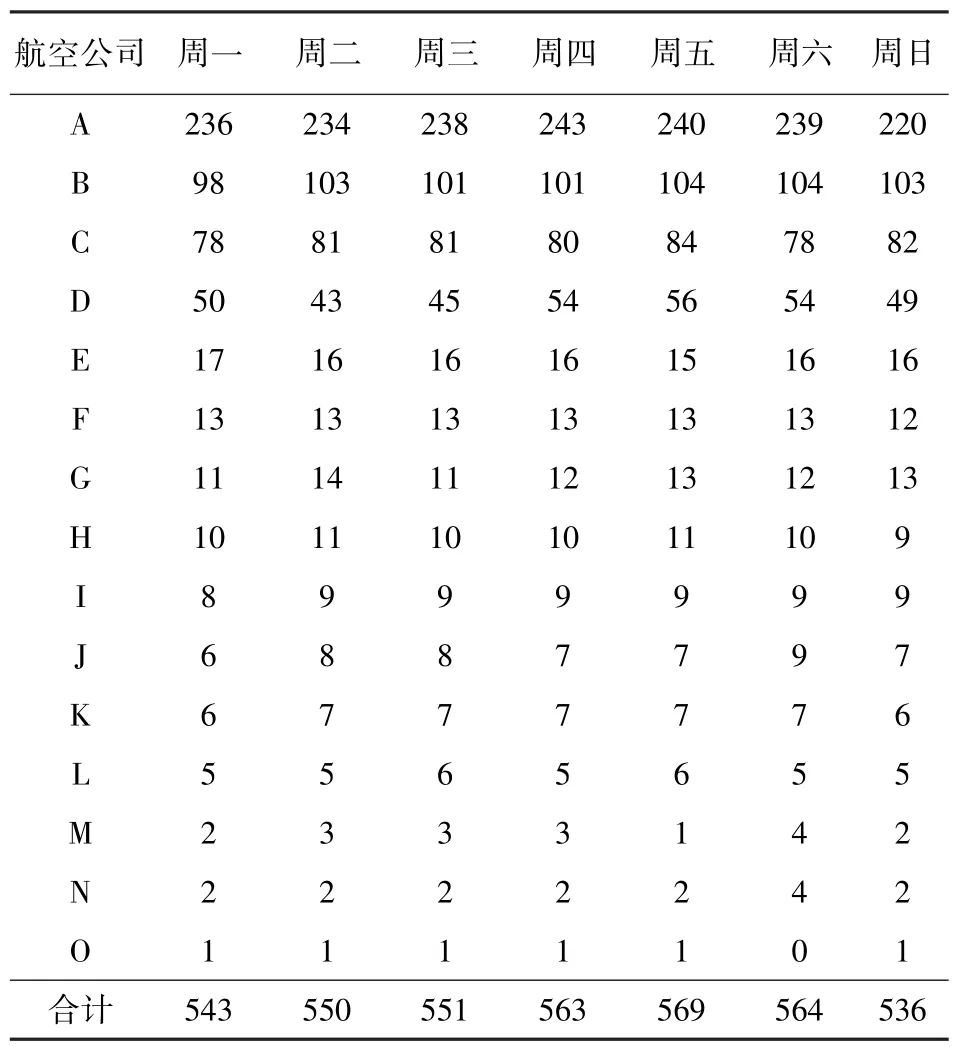
表1 各航空公司每日航班数Table 1 Flight number of each airline

表2 每日延误情况Table 2 Delay each day (min)

不同航空公司之间、同一航空公司不同时段之间的延误时长具有明显的波动性,航空公司的航班延误时间与其航班量之间基本成正比关系,航班数少的航空公司每个班次的延误时长对在当天的延误总时间影响大.图1是A、B、C三家基地航空公司每日延误总时长,图2是日航班数不超过10班的J、K、O航空公司每日延误时长.航空公司O每日一个航班,此航班延误导致其周一延误时长达到114 min.

图1 基地航空公司每日延误时长Fig.1 Delay time of base airline each day

(2)延误航班分析.

①每周不同时段航班延误.

航班延误时间多在15～40 min之间,其总数约占总航班量的43.9%,甚至高于每日正常航班数比例.周六受天气影响,取消航班高达22个;延误时间在15～40 min的航班有140个 ,正常航班91个仅有平时的一半.除去周六特殊情况,取消和延误4 h以上航班数最多的是周一,航班数分别是12个和10个,占航班总数的2.23%和1.86%;其次是周五,取消11个航班,占总航班数的1.93%.正常航班数最多是周二,占总航班数的39.2%,航班延误具体数据如表3所示.

图2 小型航空公司延误时长Fig.2 Delay time of small airlines

表3 航班延误统计Table 3 Flight delay statistics (个)

②每日不同时段航班延误.

将每小时延误航班进行累加,延误最高时段是在14:00～18:00,延误航班数为774个,延误率高达80.88%;其次是在11:00～14:00,延误航班数是566个,占总航班数的76.28%;其中延误率最低是在21:00～24:00,延误航班数为200个,延误率为57.97%.

在调查期内各个时段的延误情况来看,延误率从5:00-8:00到14:00-18:00呈上升趋势,在14:00-18:00到达最高峰,而后呈下降趋势,在21:00-24:00处于最低谷,各时段延误率变化如图3所示.

(3)各公司延误率分析.

延误率最低的是M航空公司38.89%,却是所有航空公司中平均延误时长最长的公司,同时由于其航班数很少,数据会有很大波动;其次是航空公司G,其延误率为43%;延误率最高的航空公司是L,延误率高达81.08%,虽延误率高,但其平均延误时长是所有航空公司中最短的,平均延误时长是36 min.

图3 各时段延误率变化情况Fig.3 Change of delay period

基地航空公司 A、B、C、D延误率分别为65.58%、67.65%、60.99%、60.4%,延误率最高的是航空公司B,其次是A,延误率最低的是D.四个航空公司的平均延误时间分别是47 min、45 min、45 min、39 min,平均延误时间由高到低的航空公司为航空公司A、B、C、D.航班较少的航空公司延误时长更具有偶然性,波动十分明显;航班较多的航空公司每日平均延误分别在30 min～1 h之间.从每日延误情况来看,14:00-18:00的延误率最高, 21:00-24:00的延误率最低,各航空公司延误情况如表4所示.

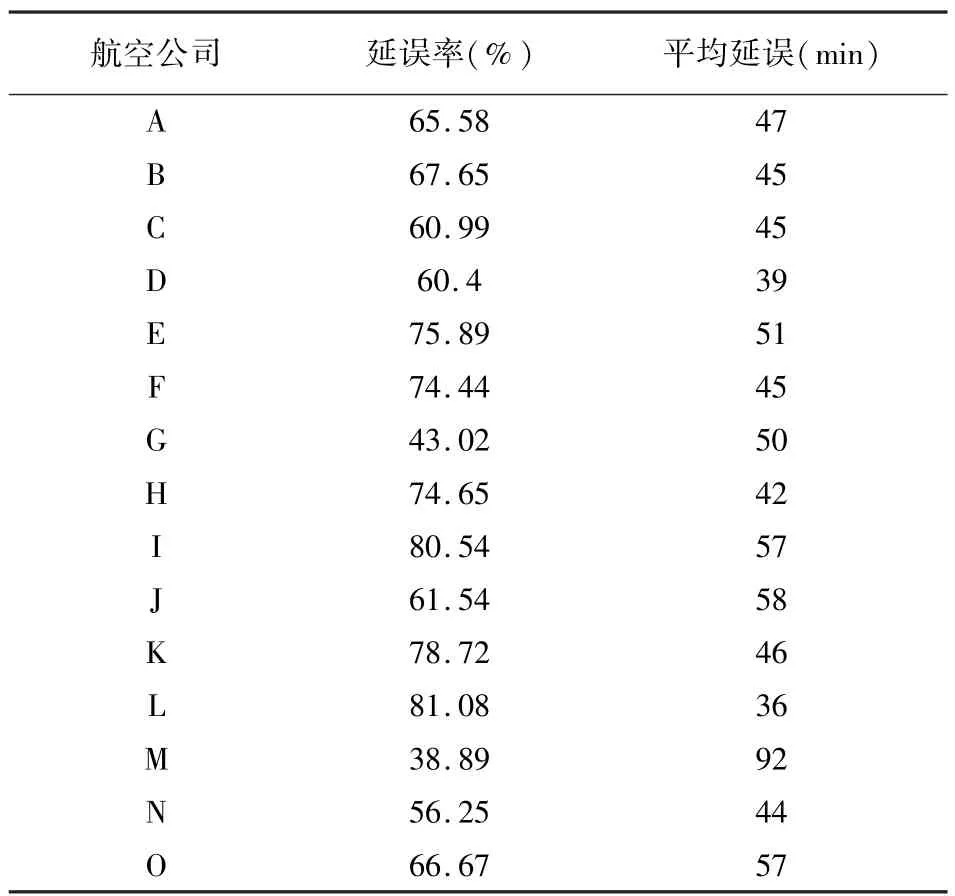
表4 各航空公司延误情况Table 4 Delay statistics of airlines

多个因素造成了首都机场的延误特点.一是首都机场日平均起降量已基本处于饱和状态,天气、流控、设备保障等因素极易引发延误;二是航班量越多,目的地机场越多,一旦目的地机场恶劣天气、流控等发生时也易造成首都机场离港航班延误;三是存在虚占时刻,难以保证航班时刻安排合理.提高机场容量、科学安排航班时刻、保障设备正常可以显著减少航班延误,而天气、突发因素造成的航班延误客观上难以避免,但可以通过寻找延误发生规律预先采取处置措施,下面分析航班延误时长的分布规律.

3 航班延误时长分布分析

航空运输系统仿真中多将航班延误时长看作正态分布,以此进行机场、航空公司的运行仿真.本文航班延误分布分析中包括延误时间在15 min以内的航班及延误航班,但不包括取消的航班.7天一共有3 816个航班,航班仿真时一般以1天作为优化时间段,航班延误时长分布规律的分析同样以天为单位.

(1)每天航班延误时长直方图.

若航班延误时长服从正态分布,则

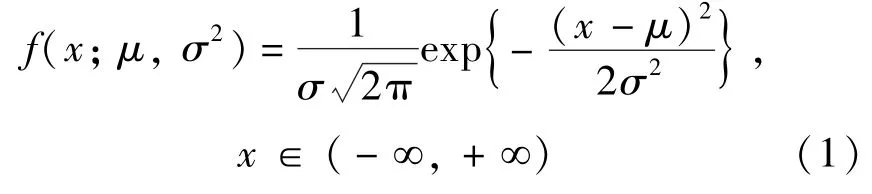
式中 σ,μ分别为延误时长的均值和标准差.

检验正态性的方法很多,如查看延误时长的直方图,如果直方图呈现大致的对称性,则初步认为服从正态分布.通过分析7天共3 816个航班的延误时长,发现有一半以上延误时长为右偏.延误时长普遍出现结构偏移的情况,即更多的延误时长高于平均延误时间.图4描绘了4天(周一、周五、周六、周日)的延误时长直方图.

在正常天气和交通管制条件下,每天的延误时长规律相似,绝大多数延误航班的时间在1 h之内,体现为绝大多数延误航班的延误时长集中,表明的延误时长的数学区分度并不好.每天的延误时长全部没有通过正态、指数等检验.

(2)延误时长的统计规律.

航班延误时长难以用参数估计方法给出延误规律,为此采用非参数估计中核概率密度估计方法.核概率密度估计是在直方图基础上演变而来的具有良好统计性质的密度估计方法,由于核密度估计方法不利用有关数据分布的先验知识,对数据分布不附加任何假定,是一种从数据样本本身出发研究数据分布特征的方法.计算某一点周围的数据分布时,充分考虑其统计特性,具体地,一元核概率密度估计的定义为,设x为随机变量,X1,X2,…,Xn为来自x的一个连续总体的样本,则在任一点x的总体密度函数f(x)的核密度估计为

式中 K()为核函数,可以选择不同核函数,如 Uniform 函 数Gauss 函 数Triangle函数((1-|u|) I(|u|≤1));h称为窗宽;n为样本容量.取不同的核函数对估计影响不大[1].但窗宽不同取值会影响到核密度函数的光滑程度,若h取较大的值,将有多的样本对x处的密度估计产生影响,并且距x较近的点与较远的点对应的核函数值差距不大,此时核密度函数的图像是较为光滑的曲线,但同时丢失了数据所包含的一些信息;若h取较小的值,只有很少的样本点对x处的密度估计产生影响,并且距x较近的点与较远的点对应的核函数差距比较大,此时核密度函数的图像不是光滑的曲线,但它能反映出每个数据所包含的信息.

图4 4天的延误时长直方图Fig.4 Delay period histogram of four days

窗宽的取值也与数据量有关,数据量越大,h取值大,亦之相反,为此通过估计量的MISE(Mean Integral Square Error)的最小值确定最优窗宽h.

利用式(4)求得调查期间每天的最佳窗宽,如表5所示.在平常延误情形下,最佳窗宽处于同一数量级4～5之间,周六的特殊天气造成了其最佳窗宽明显异于其他的调查日,达到了14.708 2.

(3)最优窗宽计算的捷径.

每天的延误分布有相似的形态,但到具体的核概率函数参数有一定差别,而最佳窗口的变化与延误总时长的变化具有相似的趋势,每天总延误时长是容易获得的数据,为此考虑能否直接用延误总时间直接得出每天延误分布的最佳窗宽,下面对窗宽与对应的延误总时间进行拟合.

表5 不同日期最佳窗宽Table 5 Optimal bandwidth of different days

选取线性拟合、对数拟合、二次多项式拟合、指数拟合、乘幂等方式进行数据拟合实验,其中二次多项式拟合优度最佳,判定系数R2=0.995 7,拟合的公式为

为验证式(5)的正确性,对被调查机场随机选取两天进行重新调查,记录每个航班的延误时间,利用式(4)和式(5)分别计算最优窗宽和拟合窗宽,其绝对误差小于0.2,此精度对于核概率密度函数的窗宽选择已经满足要求,因此仅利用延误总时间可以非常方便计算出每天延误的窗宽和核概率密度函数.

4 研究结论

(1)据调查显示,机场航班量达到一定数量条件下每天会出现取消和延误航班,应采取相应措施尽量减少取消和延误的航班数,方便旅客出行,减少航班不正常给旅客带来的不便.

(2)被调查机场延误航班占航班总数的半数以上,表明该机场容量已达到饱和状态,稍微出现的天气、流控因素会导致大面积延误发生,单一措施已不能解决这一问题,需要民航主管部门、航空公司和机场联合行动以减少延误航班比率.

(3)建立航班延误分布的核概率密度模型,在此基础上得到了利用延误总时长获得最佳窗宽的拟合函数.同时应看到核概率密度模型与机场的航班量直接相关,若是小型机场仅有为数不多的航班量是不能利用核概率密度函数.

[1]刘光才,李微微.公共问题视角下航班延误治理机制创新研究[J].北京航空航天大学学报,2011,24 (2):60-64.[LIU G C,LI W W.The innovative research from the angle ofpublic problem on governance mechanism of flight delays[J].Journal of Beijing University of Aeronautics and Astronautics( Social Sciences Edition),2011,24(2):60-64.]

[2]李杨,熊莹.航班延误的应对机理及制度形塑[J].大连海事大学学报,2011,10(3):60-64.[LI Y, XIONG Y. Solutionsmechanism and institutional shaping of flight delay[J].Journal of Dalian Maritime University(Social Sciences Edition),2011,10(3): 60-64.]

[3]姚韵,朱金福,柏明国.关于民航业航班延误服务补救的探讨[J].企业经济,2006,(10):64-66.[YAO Y,ZHU J F,BAI M G.Discussion of flight delay remedialservice about aviation industry[J]. Enterprise Economy,2006(10):64-66.]

[4]GEORGINA S,MAEL R.Determinants of delays at European airports[J].Transportation Research Part B:Methodological,2010,44(3):392-403.

[5]王红,刘金兰,曹卫东,等.航空公司航班延误预警管理模型与分析[J].计算机仿真.2009,26(4): 292-296.[WANG H,LIU J L,CAO W D,et al. Modeling and analysis of airline flight delay early warning management[J].Computer Simulation,2009, 26(4):292-296.]

[6]吕晓杰,王红.大型枢纽机场大面积航班延误预警方法研究[J].计算机工程与设计,2009,30(19): 4564-4566.[LV X J,WANG H.Method for swept flight delay early warning of large aeronautic hub[J]. Computer Engineering and Design,2009,30(19): 4564-4566.]

[7]徐涛,丁建立,王建东,等.基于贝叶斯网络的航班延误与波及分析模型[J].系统仿真学报,2009,21(15): 4818-4822.[XU T,DING J L,WANG J D,et al. Model for predicting flight delays and analyzing delay propagation based on bayesian networks[J].Journal of System Simulation,2009,21(15):4818-4822.]

[8]WONG J T,TSAI S C.A Survival model for flight delay propagation[J].Journal of Air Transport Management, 2012(23):5-11.

[9]MAHARJAN B,MATIS T I.An optimization model for gate reassignment in response to flight delays[J]. Journal of Air Transport Management,2011,17(4): 256-261.

[10]JOHNSON T,SAVAGE I.Departure delays,the pricing of congestion,and expansion proposals at Chicago O'Hare Airport[J]. JournalofAirTransport Management,2006,12(4):182-190.

Flight Delay Distribution Law at Capital Airport of Beijing

YANG Wen-dong1,HUANG Li-shi1,LIU Wan-ming1,2
(1.College of Civil Aviation,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China; 2.Transport Division,Civil Aviation Administration of China,Beijing 100710,China)

Flight delay often occurs in air transportation in recent years,which severely affects benefits of airports,airlines and passengers.Flight delay cannot be entirety eliminated because of the effects of weather,air control and human factors.However,we are able to analyze the internal reasons and underlying laws to reduce till avoid unnecessary loss.Based on statistics during a week at the Capital Airport in Beijing, China,the paper analyzes the delay length,delay rate,delay fluctuation of different airlines and different durations.It develops a kernel density evaluation function of a day delay duration distribution,and then proves that the delay duration distribution looked on as normal distribution is not accurate enough.The method to fit optimal bandwidth is presented.The result shows that the method meets the accuracy request to analyze flight delay,which provides reference for analyzing operation and recovery for abnormal flights.

air transportation;flight delay;delay duration distribution;kernel density evaluation function

U15

A

U15

A

1009-6744(2013)02-0199-06

2012-11-14

2012-12-17录用日期:2013-01-09

国家软科学研究项目(2011GXQ4B023).

杨文东(1975-),男,山东寿光人,副教授,博士.

*通讯作者:ywendong@nuaa.edu.cn