地面交通拥堵对民航旅客航班时刻选择的影响

陈 蒂,张 宁,刘 健

(北京航空航天大学经济管理学院,北京100191)

地面交通拥堵对民航旅客航班时刻选择的影响

陈 蒂,张 宁*,刘 健

(北京航空航天大学经济管理学院,北京100191)

研究了高峰期地面交通拥堵对民航旅客航班时刻选择行为的影响.在考虑地面交通瓶颈的基础上建立了民航旅客出发时间选择模型,给出了模型的用户均衡的性质.并进一步分析了票价差额对用户均衡的影响,得到了均衡人数不变时票价差额的取值范围,以及民航旅客的总排队时间和航空公司票价增量收益随票价差额变化的特征.研究表明:在均衡状态下,选择不同时刻航班的旅客人数由航班时刻差和瓶颈通行能力共同决定.对给定的航空出行需求,可通过调整票价差额,减少总排队时间(减缓交通拥堵)或者增大票价增量收益(增加航空公司票价收益).最后利用数值算例对结论进行了有效验证.

综合交通运输;航班时刻选择;瓶颈模型;航空运输;拥堵

1 引 言

随着经济的快速发展,航空出行已经成为城市间交往的重要交通方式.但由于航空出行需求的迅速增长,各大机场进场道路常常在高峰期出现交通拥挤而形成瓶颈状态,极大地降低了航空服务质量及旅客出行效率.人们在选择航空出行时会考虑到机场地面交通的拥堵程度,即地面交通拥堵对民航旅客选择航班时刻有作用,此现象是一个非常值得深入研究的学术问题.对航空公司来说,如何针对不同的航班时刻,制定价格策略来降低地面交通拥堵,增加经济效益,也是一个需要深入探究的实际问题.

目前研究民航旅客出行时间选择的文献并不多见,许多学者主要通过研究需求运量预测[1,2]、顾客对航班的满意度测评[3]、航班时刻和机票价格两个因素的竞争[4,5]等对民航旅客出行特征进行分析和论证,来最大化航空公司和民航旅客的收益.这些研究都是针对航班特性的,没有考虑地面交通对民航旅客出行的影响.本文用一个简明模型来揭示地面交通拥堵对民航旅客出行选择的影响原理.著名的瓶颈模型是由诺贝尔经济学奖得主Vickrey在1969年提出的,是首次应用确定性排队理论建立的、令所有出行者具有相同交通出行费用的内生出发时间选择模型[6].该模型简单、直接地透析了出行者的出发时间选择机理.瓶颈模型提出之后,得到了全球有关学者的广泛关注,并进行了广泛的拓展研究[7-10],但较少对其在航空旅客出行中的应用进行分析.

本文对瓶颈模型进行拓展,考虑同一航空公司两个不同时刻的航班可供民航旅客选择,民航旅客需要经过一段包含交通瓶颈的道路到达机场,简洁地构建出考虑地面交通拥堵的针对民航旅客的出发时间选择模型,确定了均衡状态下民航旅客出行的规律.最后通过分析票价差额对均衡的影响,得到了一个重要结论:对给定的航空出行需求,科学调整票价差额,即可减少民航旅客的总排队时间或增加航空公司的票价增量收益.

2 基本模型及其性质

2.1 基本模型

已知A机场每天有两班航班到B机场,第一班起飞时刻为t*1,第二班起飞时刻为t*2,不妨设t1*＜t2*.N个同质的民航旅客在高峰期需要通过某条道路到达A机场乘飞机到B机场,该条道路包含一个通行能力为s的瓶颈.假定民航旅客对航班时刻无偏好,可以早到,不允许迟到,忽略登机时间.其中N1个民航旅客选择第一班飞机,称为第一类出行者,N2个民航旅客选择第二班飞机,称为第二类出行者.本文考虑民航旅客的出发时间选择问题.

民航旅客出行费用包括排队时间成本、早到惩罚和机票价格,为使模型更加简明,首先考虑两个航班的机票价格相同,不妨设为0.那么对两类出行者,单个出行者的出行费用

式中 t为出行者出发时刻;T(t)为t时刻出发的出行者在瓶颈处的排队时间;α为单位排队时间费用;β为单位早到时间费用(α＞β).另外记第i类出行者的最早出发时刻为tai,第i类出行者准时到达(t*

i时刻到达)的出发时刻为tbi,因不允许迟到,此即为第i类出行者的最后出发时刻.

设民航旅客有出发时间的完全信息,因此在均衡状态,所有旅客的出行费用是相同的,任何出行者都不能通过单方面改变出发时间来减少出行费用.在两类出行者独立出行、互不影响的前提下,对第一类出行者:

最早出发的人没有排队时间,其出行费用为

最后出发的人正好在t1*时刻到达(没有早到惩罚),其出行费用为

在整个出发期间,瓶颈全能力负荷运行.因此

结合式(2)-式(4)和等费用条件可得

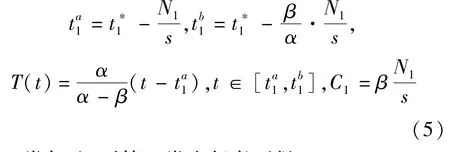
类似地,对第二类出行者可得2.2 模型性质

下面就航空出行需求N讨论均衡状态存在的条件,分析均衡存在的规律.均衡状态下所有出行者出行费用相同,即C1=C2.设航班时刻差Δt=t2*-t1*,下面的引理1和引理2给出了由于地面交通瓶颈的存在,第二类出行者人数N2对均衡的影响.

引理1 若N2＞Δt·s,则用户均衡不存在.

证:因瓶颈通行能力有限,在t1*和t2*之间到达的出行者人数最多为Δt·s.若N2＞Δt·s,因不允许迟到,此时第二类出行者必然有部分要在t1*时刻之前到达,两类出行者出现交织出发并混行的现象.t时刻出发的两类出行者混行,其排队时间T(t)必然相等,且t+T(t)＜t1*,则其出行费用分别为

显然C1＜C2,因此与均衡状态下所有出行者出行费用相同矛盾.证毕.

引理1说明均衡状态下,由于瓶颈通行能力的限制,选择航班时刻为t2*的民航旅客(第二类出行者)人数不会多于Δt·s.

引理2 若N2＜Δt·s,当且仅当N1=N2时,用户均衡存在.

证:若N2＜Δt·s,由公式(6)知t*,则此时两类出行者独立出行且相互无影响.根1据式(5)、式(6),当且仅当N1=N2时,有C1=C2,即达到均衡状态.证毕.

引理2说明均衡状态下,选择航班时刻为t2*的民航旅客少于Δt·s时,选择航班时刻为t1*的民航旅客必与选择航班时刻为t2*的民航旅客人数相等.

于是下面就航空需求N的取值,分析均衡状态下民航旅客出行的规律,并用下面的定理1和定理2表述.

定理1 当N≤2Δt·s时,均衡状态下必有N1=N2.

证明:若N2＞Δt·s,则由引理1知不可能达到均衡状态.若N2≤Δt·s,则根据引理2,均衡状态下必有N1=N2.证毕.

定理1表明,当航空出行需求N小于等于阈值2Δt·s时,均衡状态下第一类出行者和第二类出行者人数相等且出发时刻、排队时间互不影响,相互独立.即此时,选择两个航班的民航旅客人数是相等的.

根据引理1和引理2知,当航空出行需求N＞2Δt·s时,均衡状态下,N2=Δt·s.此时第二类出行者最早出发的到达时刻为t*1,对第一类出行者的均衡不产生影响,因此第一类出行者的出发时间和费用仍为式(5).又均衡状态下C1=C2,此时第二类出行者的第一个出发者必须在第一类出行者全部通过瓶颈之前出发,在瓶颈处经过一段时间的排队,在t*1时刻提前到达,即有

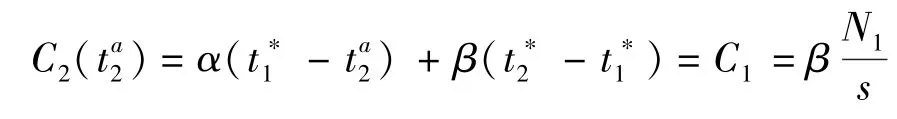
得到最早出发时刻

最晚出发的第二类人准时到达,其费用为

于是可得定理2如下.

定理2 当N＞2Δt·s时,均衡状态下,必有N2=Δt·s,第一类出行者的出发时刻、排队时间和出行费用仍为式(5).但第二类出行者的出发时刻、排队时间和出行费用分别为

得到最晚出发时刻即与式(6)相比,第二类出行者排队时间增加·出行费用相应地也增加

定理2表明,当航空出行需求 N大于阈值2Δt·s时,均衡状态下,第二类出行者人数由航班时刻差和瓶颈通行能力共同决定,即为定值Δt·s,其余旅客均为第一类出行者.也即此时,选择第一个航班的人数多于选择第二个航班的人数.记N*=2Δt·s,称为航空出行需求阈值.

3 票价差额调控的有效阈值

设两个航班票价差额Δp=p2-p1,其中p1、p2分别为两个航班的票价.对给定的航空出行需求N,若已知选择第一个航班的人数为N1,选择第二个航班的人数为N2,则航空公司票价总收益为G= N1p1+N2p2.基本模型中假设两个航班票价一样,即Δp=0,不妨设p1=0,此时票价总收益G0=0.实际上,航空公司可对不同航班制定不同的价格策略,记ΔG=G-G0,称为航空公司票价增量收益,则有ΔG=N2Δp.本节讨论票价差额Δp的取值对总排队时间TT和票价增量收益ΔG的影响.

考虑当N≥N*时的情形:

用户均衡状态下,若Δp=0,两类出行者人数为N1=N-Δt·s,N2=Δt·s.首先讨论保持均衡人数不变时,Δp的取值范围.此时第一类出行者排队时间、出行费用不变,仍为式(5),第二类出行者的个人出行费用与第一类出行者相同C2=C1=β即有

于是得

为使第二类出行者在t2*之前全部到达,第一个第二类出行者的出发时间最晚为t1*,最早为最后一个第一类出行者的出发时间tb1,即满足tb1≤ta2≤t*1,结合式(5)、式(11)得 -βΔt≤ Δp≤

因此当N≥N*时,当且仅当-βΔt≤Δp≤β时,均衡人数与Δp=0时相同.总排队时间票价增量收益ΔG=(Δt·s)·Δp.

当Δp＜-βΔt时,第二个航班的出行费用比第一个航班出行费用低,由于瓶颈通行能力的限制,第二类出行者必有部分在t1*之前到达.因此,均衡时,所有人选择第二个航班,此时总排队时间TT=票价增量收益ΔG=N·Δp.

类似地可对N＜N*时的情形进行讨论.

因此,对给定的航空出行需求N,总排队时间TT和票价增量收益ΔG分别为

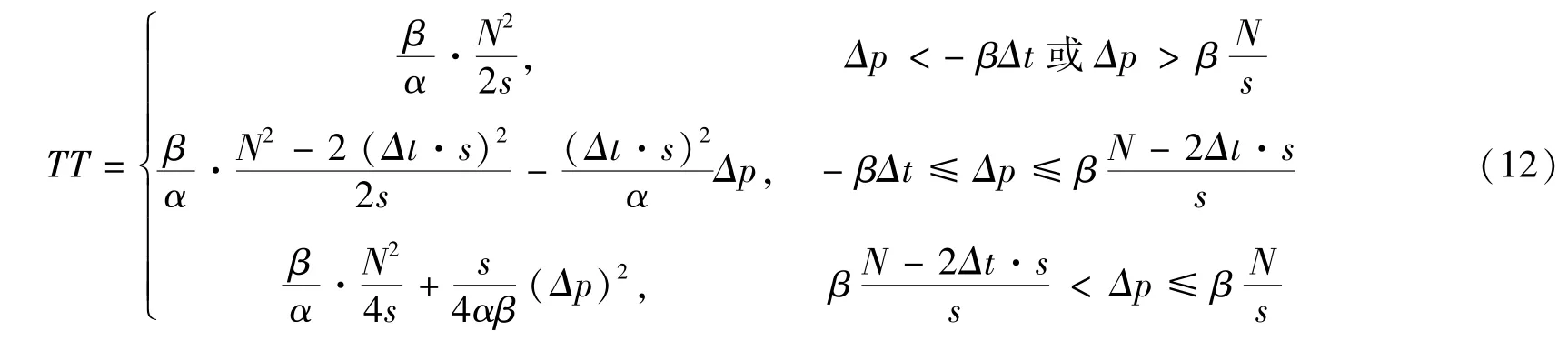
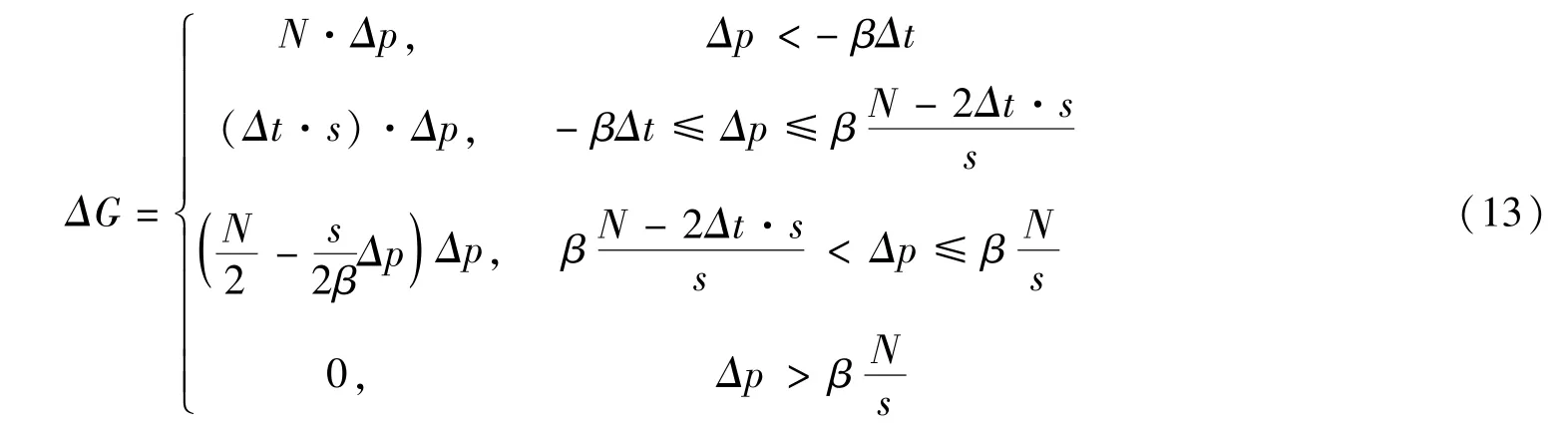
根据式(12),对给定的航空出行需求N,当Δp＜-βΔt时,所有民航旅客选择第二个航班,当时,所有民航旅客选择第一个航班,此时总排队时间 TT为常数,票价差额调控失效.当时,若N≥N*=2Δt·s,当时,在瓶颈处总排队时间TT最少;若N＜N*,当Δp=0时,在瓶颈处总排队时间TT最少.

4 算例分析

下面通过两个算例验证:(1)当出行需求已知时,选择不同航班的出行者人数由航班时刻差和瓶颈通行能力共同决定.(2)对给定的航空出行需求,科学安排票价差额,可减缓地面交通拥堵或增加航空公司票价收益.

4.1 算例1

设航空出行需求N=1 200 P,图1给出了民航旅客选择不同航班时刻的决策空间.曲线O1O2表示Δt·s=600 P,在区域A,选择两个航班的民航旅客人数相等,均为600 P,两类出行者独立出行,互不影响.在区域B,选择第一个航班的旅客人数多于选择第二个航班的旅客人数,且选择第二个航班的旅客人数由航班时刻差和瓶颈通行能力共同决定,即为N2=Δt·s,其余旅客均选择第一个航班,即N1=N-N2.例如,区域B中,在点(Δt,s)=(20 min,10 P/min)时,选择第二个航班的人数即为200 P,选择第一个航班的则为1 000 P;在点(Δt,s)=(30 min,15 P/min)时,选择第二个航班的人数即为450 P,选择第一个航班的则为750 P.可见,对固定的航空出行需求,两类出行者的人数由航班时刻差和瓶颈通行能力共同决定.

图1 民航旅客选择不同航班时刻的决策空间Fig.1 The decision space for flight choice among aviation passengers

4.2 算例2

设航班时刻t1*=7:00,t2*=8:00,瓶颈处通行能力s=10 P/min,单位排队时间费用和早到时间费用分别为α=1 yuan/min,β=0.5 yuan/min.计算得航空出行需求阈值N*=2Δt·s=1 200 P.

图2给出了对不同的航空出行需求N,民航旅客总排队时间TT随票价差额Δp的变化特征.当Δp＜-30或Δp＞时,所有旅客选择同一航班出行,总排队时间TT为常数,不随票价差额发生变化.在-30≤Δp≤时,代表典型特征分两种情况:

(1)当N=800(＜1 200)时,在区间[-30,0],随着票价差额Δp的增大总排队时间TT减少,在区间[0,40],随着票价差额Δp的增大,排队时间TT增加.在Δp=0(A1点)时,选择两个航班的旅客人数相等,TT取得最小值.

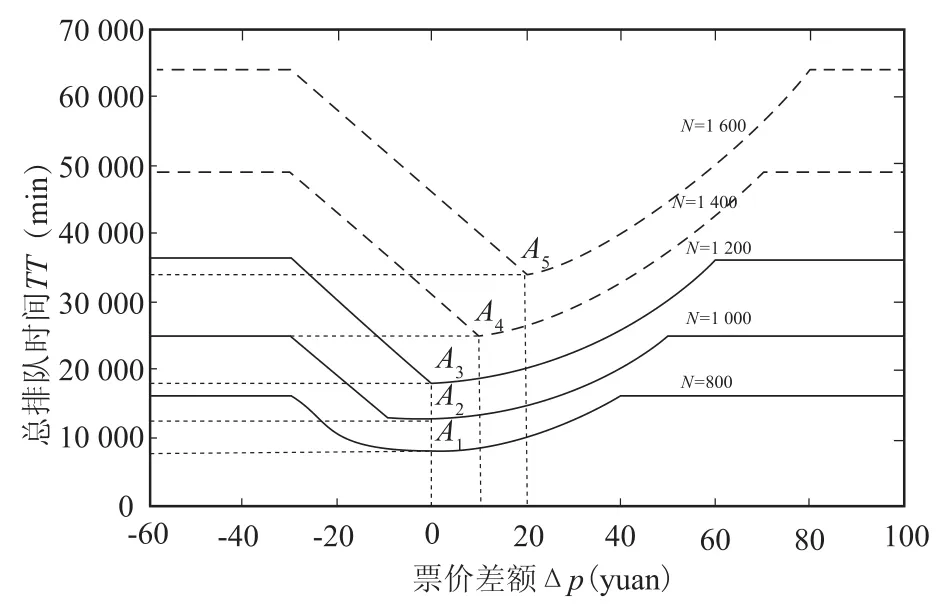
图2 票价差额对总排队时间的影响Fig.2 The effect of different airfares on total queuing time

(2)当 N=1 600(＞1 200)时,在区间[-30,20],随着票价差额Δp的增大总排队时间TT随之而减少,在区间[20,80],随着票价差额Δp的增大排队时间TT增加.在Δp=20(A5点)时,选择第二个航班的人数恰好为两个航班时刻间瓶颈能通过的出行者人数,且选择两个航班的旅客独立出行、互不影响,此时TT取得最小值.

这一现象说明,若航空出行需求比较小,当两个航班的机票价格一样时,总排队时间最少;若航空出行需求足够大,当第二个航班的机票价格适当高于第一个航班的机票价格时,总排队时间最少.因此,可通过科学安排机票价格差额,使总排队时间减少,减缓交通拥堵.

图3给出了对不同的航空出行需求N,航空公司票价增量收益ΔG随票价差额Δp的变化特征.当Δp≤时,票价增量收益ΔG随票价差额Δp的增大而增加,当Δp＞时,票价增量收益ΔG随票价差额Δp的增大而减少,直到Δp=之后票价收益增量为0.当Δp=(B点,i=1,i2,3,4,5)时,票价增量收益ΔG最大.由于本文为简化问题,提炼规律,只考虑了民航旅客对航班时刻选择无偏好的情形,因此在不存在地面交通瓶颈的条件下,调整票价差额导致民航旅客全部选择票价低的航班,不影响票价增量收益;在存在地面交通瓶颈的前提下,对给定的航空出行需求,可通过适当调整票价差额,增加航空公司票价增量收益.

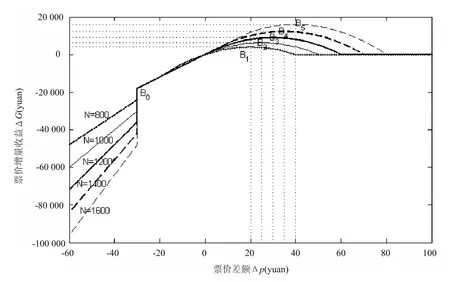
图3 票价差额对票价增量收益的影响Fig.3 The effect of different airfares on incremental revenue

5 研究结论

首先,本文证实了地面交通拥堵对民航旅客选择航班有重大的影响.当出行需求比较小时,在出行费用均衡的条件下,不同航班的旅客对交通拥堵的影响是独立的,如果两个航班的票价一致,选择两个航班的旅客人数分布相同;当出行需求足够大时,在出行费用均衡的条件下,后续航班的旅客受前期航班旅客出行的影响,后续航班旅客的地面交通瓶颈制约高于前期航班,在票价不变的前提下,民航旅客倾向于选择前期航班出行.其次,本文构建了票价差额调节策略:一方面通过适当提升票价差额,可以减少总排队时间,减缓地面交通拥堵;另外一方面较大程度地提高票价差额,可以提高票价增量收益,增加航空公司收益.

上述结论与现实情况是相符的.但本研究为了简洁地揭示地面交通拥堵对民航旅客出行选择的影响,在建模时作了大量的简化,与实际交通状况还是有一定的距离.因此,根据实际情况,进一步深入考虑航班时刻偏好、航班舒适度及准点率,或引入弹性航空出行需求,增加更多的航班时刻等.研究复杂条件下的航空旅客出行规律,是未来值得深入探讨的科学问题.

[1]Coldren G M,Koppelman F S.Modeling the competition among air-travel itinerary shares: GEV model development[J].Transportation Research Part A: Policy and Practice,2005,39(4):345-365.

[2]Koppelman F S,Coldren G M,Parker R A.Schedule delay impacts on air-travel itinerary demand[J]. Transportation Research PartB: Methodological, 2008,42(3):263-273.

[3]毛曼,朱金福.航空公司顾客满意度测评模型及实证研究[J].交通运输系统工程与信息.2010,10 (005):201-207.[MAO M,ZHU J F.Airlines customer satisfaction testing model and case study[J]. Journal of Transportation Systems Engineering and Information Technology,2010,10(5):201-207.]

[4]Schipper Y,Nijkamp P,Rietveld P.Deregulation and welfare in airline markets:An analysis of frequency equilibria[J]. European JournalofOperational Research,2007,178(1):194-206.

[5]Brueckner J K,Flores-Fillol R.Airline schedule competition[J].Review of Industrial Organization, 2007,30(3):161-177.

[6]Vickrey W S.Congestion theory and transport investment [J].The American Economic Review,1969,59(2): 251-260.

[7]Arnott R,De Palma A,Lindsey R.The welfare effects of congestion tolls with heterogeneous commuters[J]. Journal of Transport Economics and Policy,1994,28 (2):139-161.

[8]吴子啸,黄海军.瓶颈道路使用收费的理论及模型[J].系统工程理论与实践.2000,20(1):130-133.[WU Z X,HUANG H J.The pricing theory and models in a highway with bottleneck[J].Systems Engineering-Theory& Practice, 2000, 20(1): 130-133.]

[9]吴文祥,黄海军.考虑地铁车内拥挤和早到与迟到惩罚的通勤者出发时间选择模型[J].交通运输系统工程与信息.2009,9(1):128132.[WU W X, HUANG H J.Model of subway commuters'departure time choice with in-carriage congestion and arrival early/late penalty[J]. JournalofTransportation SystemsEngineering and Information Technology, 2009,9(1):128-132.]

[10]Liu Y,Nie Y M.Morning commute problem considering route choice,user heterogeneity and alternative system optima[J]. Transportation Research Part B: Methodological,2011,45(4):619-642.

Effect of Road Traffic Congestion on Aviation Passenger's Flight Choice

CHEN Di,ZHANG Ning,LIU Jian
(School of Economics and Management,Beihang University,Beijing 100191,China)

This paper investigates hovo passengers choose flight times in view of ground traffic congestion. The departure time choice model of aviation passengers is developed by extending Vickrey's bottleneck model.The conditions are determined for the existence of the user equilibrium in the model.Then,the range of the difference between the airfares is established while the number of aviation passengers choosing the same flight time remains unchanged at the user equilibrium.Moreover,the tendency of the total queuing time and the incremental airfare revenue is derived along with the difference between the airfares.The results show that the number of aviation passengers is jointly determined by the flight time and the bottleneck capacity for different schedules.Under the given passenger volume,the total queuing time(traffic congestion)can be reduced or the incremental airfare revenue can be increased by properly adjusting the airfares'difference.Two numerical examples are presented to demonstrate the principle and its application.

integrated transportation;flight choice;bottleneck model;air transportation;congestion

U121

A

1009-6744(2013)02-0096-07

U121

A

2012-11-13

2012-12-15录用日期:2013-01-09

国家自然科学基金资助项目(70971003).

陈蒂(1981-),女,河南舞阳人,博士生,讲师.

*通讯作者:nzhang@buaa.edu.cn