广义Gamma分布簇广义线性混合模型的参数估计

谢远涛，杨 娟,徐梅笛

（1.对外经济贸易大学a.保险学院;b.国际经济贸易学院，北京 100029；2.中国人民大学统计学院，北京 100872）

0 引言

广义Gamma分布簇广义线性混合模型与广义线性混合模型乃至广义线性模型的关键区别是，变量不再满足指数分布簇，因此，统计推断问题变得异常复杂，本文主要讨论广义Gamma分布簇广义线性混合模型的参数估计问题。

自1972年Nelder和Wedderburn引进广义线性模型以来，学者一直尝试在更广义的分布中建立模型，如指数分布簇，单参数Gamma分布（Clayton and Cuzick,1985），正则稳态分布（Hougaard,1986），逆高斯分布(Hougaard,1986)，对数正态分布（McGilchrist and Aisbett,1991）。

同时，不断引入异质性来增强模型的适应性。Zeger,Liang and Albert(1988)集中在纵向数据系统讨论了随机效应模型的建模问题。Gurka et al.(2006)把Box-Cox变换推广到线性混合模型，He and Lawless(2005)建立了一类位置-尺度模型。随机效应模型与重复观测效应结合起来分析，最终产生了广义线性混合模型，模型参见Jiang（2007）。

国内对广义线性混合模型的研究文献极少，谢远涛和杨娟（2010）构造了广义Gamma分布簇广义线性混合模型，充分利用响应变量之间的相关性结构，在变量满足广义Gamma分布簇时能有效降低模型误设的风险，但是作者没有展开分析参数的估计问题。

参数估计等推断的前提是构造似然函数，那么对随机效应的处理，无论是条件似然法还是极大似然法都会遇到很多麻烦。

Zeger,Liang and Albert(1988)集中在纵向数据系统讨论了随机效应模型的建模问题。关于随机效应部分建模，这里有两种不同的思路。第一种思路是把ui当作扰动（nuisance）变量，仅仅使用不包含ui信息的那部分数据来对特定系数进行推断。这被称为总体平均法（PA，population-averaged）。第二种思路被称为个体设定方法（SS，subject-specific），该法重点关注单个个体随机效应u的估计，以及它与总体参数也即固定效应β之间的关系。这里把ui看作来自某一分布的若干独立样本，同时估计固定效应βi和随机效应ui。

在随机常数项模型中，在这两种推断方法之间的选择导致使用横截信息与使用纵向信息的不同。第一种思路仅仅使用了纵向信息，也即，在个体内进行比较来估计ui。而第二种思路中假定ui满足一个分布，我们可以同时考虑纵向数据信息和横截信息，相应的每个数据源的权重由ui的变动性来确定。

这两种思路的选取将直接影响似然函数的构造。第一种思路产生了偏似然估计，包括条件似然估计和边际似然估计；第二种思路产生了完全似然估计，后者要复杂很多。

一些学者选择偏似然方法（Cox,1975）进行边际模型估计，偏似然是边际似然和条件似然的推广。而Fraser（1968）、Kalbfleisch and Sprott(1974)早已对边际似然和条件似然进行了研究。

完全似然方法也有不少学者研究，其中最关键的一步是对似然函数的推广。Wedderburn(1974)提出拟似然（quasi-likelihood）函 数 ，在 McCullagh(1981)、McCullagh and Nelder(1989)的文献中有系统论述。

拟似然的提出为一大类模型提供了推断的基础。对于大多数非正态模型，需要使用数值积分（如Crouch and Spiegelman,1990）。在阶数取更高的时侯，可以使用Mon-te Carlo积分方法。Li and Raghunathan（1991）在先验分布中使用重要重复抽样（或者Gibbs抽样来回避数值积分（Zeger and Karim，1991）。对于求解极大似然估计，最常用的是EM算法（Dempster等，1977）。

到了后来，一些基于近似的方法逐渐提出并占主流地位。这类近似方法包括Laplace近似方法（Tierney等1989）和Taylor序列展开式方法。后文会有详细的论述。

这些参数估计理论非常丰富，但前提是，这些估计思想只适用于正态分布，或者指数分布簇，对于含随机效应项的广义Gamma分布簇，尚缺乏研究结果。

本文将重点讨论广义Gamma分布簇广义线性混合模型的参数估计问题。这类模型的参数估计理论没有公开发表，这是本文的创新点。另外，本文在推断上广泛应用广义线性混合模型的研究成果，这是本文的特点。

1 模型与对数拟似然函数的构建

广义Gamma分布簇广义线性混合模型可以用矩阵形式来表述如下：

其中，η为线性预测，等于连接函数g(μ)，μ为条件均值。X是固定效应解释变量矩阵，β是固定效应系数向量，Z是随机效应设计矩阵，u是随机效应系数向量，均值为0，协方差矩阵为G，后文中常常用到的假定是随机效应项满足MVN（0，G）分布，e是扰动项，协方差矩阵为R。记为：

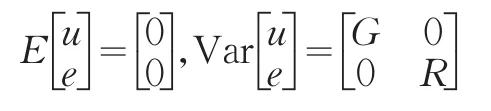
设该协方差结构中包含的未知参数为φ。此框架下，可以同时设定随机效应的方差结构G和重复观测效应方差结构R。

如果yi是来自广义Gamma分布的随机样本，构造对数拟似然函数写成标准参数形式为：

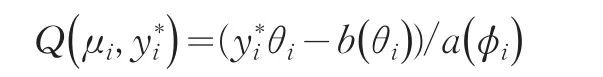
2 参数估计

本文讨论的参数估计方法是基于近似的一类估计方法。主要根据拟似然、伪似然、边际似然构建极大似然估计和受限极大似然估计。6种参数估计的方法，也即罚拟似然、边际拟似然、伪似然的ML估计和REML估计，尽管理论假设不同，分析思路不同，但是最终的估计形式惊人的一致。

罚拟似然（PQL）方法基本思想是把完全似然函数用Laplace方法来近似，通过对对数似然函数关于参数δ偏导并令其等于零来构造得分方程，然后我们可以通过求解一些得分方程来找到极大似然估计。

边际拟似然（MQL）方法的最大优点是稳健性，即使方差成分误设，广义估计方程仍然能提供固定效应的一致性估计，当然前提条件是一阶矩设定正确它的一个特点是可重复性和容易实施，通过重复调用常规正态分布观测值方差分析软件就可以用来估计非正态分布模型，如重复调用广义最小二乘来估计广义线性模型。因此这种方法很流行。

Breslow and Clayton(1993)同时对两种方法进行系统介绍和比较，为把得分方程组的求解转化为迭代方式求解提供了理论支持，具体求解使用的方法是迭代（再）加权最小二乘算法（Nelder and Wedderburn,1972）。Vonesh等（2002）同时扩展了罚拟似然方法和广义估计方程，在估计方程中引入了一二阶条件矩。Lin等（1997）进一步把协变量效应引入到方差成分中。

Wolfinger and O’Connell（1993）使用的伪似然方法在实际编程应用中有重要地位。伪似然（Carroll and Ruppert，1988,P71）是指“伪称其他回归参数β已知并且等于当前的估计值进一步基于正态性假定得到参数θ的极大似然估计。”伪似然实施过程中，是轮流估计参数β和θ，迭代直到收敛。如果在估计随机效应协方差矩阵G和残差协方差矩阵R的参数时使用了ML方法，那就得到PL估计量;如果在估计随机效应协方差矩阵G和残差协方差矩阵R的参数时使用了REML方法，那就得到REPL估计量。伪似然方法提供了SS推断和PA推断的统一的框架，并且把PQL和MQL作为特例包含进来。而且，该方法可以允许自定义G和R的协方差结构以适应更一般的模型。更重要的一点是，PL或REPL方法可以很方便地利用SAS的固有线性混合模型模块来实现。

Davidian and Giltinan(1993)讨论了两类非线性混合模型的估计方法，一种他们称为pooled two stage（PTS）法，另外一种他们称为线性化混合效应（LME）方法。PTS法对从每个个体得到的估计进行合成；LME方法是Vonesh and Carter（1992）线性化方法的推广。Wolfinger and O’Connell（1993）伪似然方法与LME方法非常相似，不同之处在于，LME对于随机效应的线性化是0，但Wolfinger and O’Connell（1993）的方法以及Lindstrom and Bates（1990）的方法都对参数的当前估计进行线性化。

总结一下，Breslow and Clayton(1993)利用拟似然总结了PQL和MQL两种方法，但最终以特例形式在Wolfinger and O’Connell(1993)的伪似然方法中体现出来。同时，伪似然方法与LME方法思路非常相似，只是在线性近似处理上有所不同。

综合这些模型，得出本模型参数估计的基本思路如下：

首先固定τ，伪称其估计已知τ=τ̂，然后讨论其余参数的估计，最后基于搜索算法求的使所有参数估计最优的τ̂。

具体说来，通过使用Laplace近似的方法（Tierney等1989）或者Taylor序列近似，可以得到目标似然函数的线性近似或者分析近似，构造出得分方程组，求解都可以运用Fisher得分法得到迭代（再）加权最小二乘估计。也即可以通过下面的方程组以迭代方式求解β和u：

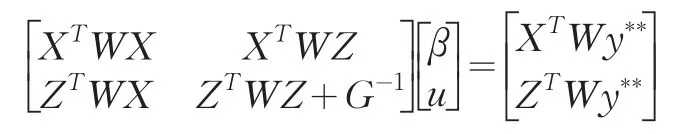
然后可以得到随机效应的收缩估计：

迭代（再）加权最小二乘法迭代求解的时候要求Ĝ非奇异。但是在迭代运算的过程中，常常会出现迭代估计失败造成方差成分取边界值0。如果奇异，需要使用Cholesky分解进行调整(Henderson 1984)。

设是̂的Cholesky下三角根那么迭代（再）加权最小二乘法方程组变为：

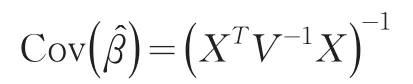
而且，这个结论还可以推广，如果把V用一致性估计替换，以上渐进性依然成立。

把这些参数估计带入到目标似然函数，得到调整后参数ϕ的近似概括拟似然函数，利用这个公式关于ϕ偏导并令其为0，得到得分方程，基于此可以求解

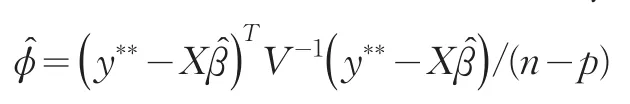
在建模过程中假定尺度参数φ=1可以得到Breslow and Clayton的罚拟似然方法（penalized quasi-likelihood,PQL）；而 Wolfinger and O’Connell方法为伪似然方法（pseudo-likelihood,PL）或者受限伪似然方法（restricted pseudo-likelihood,REPL），在建模过程中假定尺度参数φ是未知的，因此利用PL得到尺度参数的极大似然估计或者利用REPL方法获得尺度参数的受限极大似然估计。从这种意义上说，罚拟似然方法只是伪似然方法中尺度参数φ=1的特例。

利用前面的方法可以得出固定τ下的参数估计，假定为，把它们带回联合似然函数，得到联合似然函数的估计式

因为y*=yτ，在τ＞0时为单调函数，那么τ的估计可以直接对联合似然函数极大化来求解：

本文设计非对称有记忆二分搜索算法：

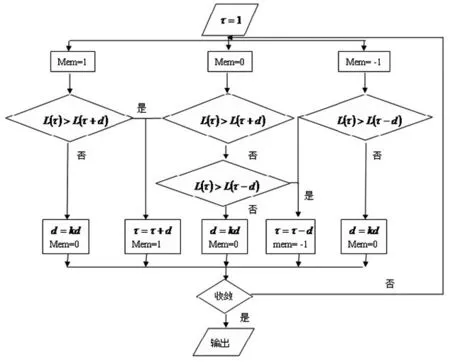
图1 直接搜索算法流程图

纵观算法，运算不外乎两类：一是τ的变化，二是步长d的变化。我们把τ的变化（加减d个步长）定义为延展，把τ不变化而步长改变定义为收缩。一旦运算进入收缩阶段，就会收敛到最小值，当然，这个最小值可能是局部最小值。

初始化时可以选择τ=1，初始化步长d，d的取值不易大于1，防止τ取负，同时，d的取值不易太小，以防解收敛于局部最小值；该算法对往正方向移动还是往负方向移动是非对称的。k为步率，反映了调整步长的程度。当τ的解往正方向或负方向移动时，步长不改变，恒定为；但是，一旦发现无论是正方向移动还是负方向移动都失败时（极值点出现在当前估计值的(τ-d,τ+d)区间上），程序会自动调整步长为原来步长的k倍，以防止出现来回震荡的情况。

3 结论

本文提出了广义Gamma分布簇广义线性混合模型的参数估计方法，该方法充分利用了指数分布簇广义线性混合模型参数估计的结果，并且参数估计表达式上与6种广义线性混合模型参数估计结果形式相同，但是模型假设和表示的含义有异。而且，该方法可以通过反复调用广义线性混合模型中的参数估计模块来实现，具有渐进正态性，因此有较好的易用性。

[1]谢远涛，杨娟.广义Gamma分布簇广义线性混合模型的构建[J].统计研究，2010,(10).

[2]Nelder J A,Wedderburn R W M.Generalized Linear Models[J].Jour⁃nal of the Royal Statistical Society,Ser.A,1972,(135).

[3]Clayton D G,Cuzick J.Multivariate Generalizations of the Proportion⁃al Hazards Model(with Discussion)[J].Journal of the Royal Statistical Society,Ser A,1985,(148).

[4]Hougaard P.A Class of Multivariate Failure Time Distributions[J].Biometrika,1986,(73).

[5]Hougaard P.Survival Models for Heterogeneous Populations Derived from Stable Distributions[J].Biometrika,1986,(73).

[6]McCullagh P,Nelder J A.Generalized Linear Models(2ndEdtion)[M].London:Chapman&Hall/CRC,1989.

[7]Zeger S L,Liang K Y,Albert P S.Models for Longitudinal Data:a Generalized Estimating Equation Approach[J].Biometrics,1988,(44).

[8]Geert Verbeke,Geert Molenberghs.Linear Mixed Models for Longitu⁃dinal[M].New York：Springer,2000.

[9]Gurka M J,Edwards L J,Muller K E,Kupper L L.Extending the Box-Cox Transformation to the Linear Mixed Model[J].Journal of the Royal Statistical Society,Ser，A,2006,(169).

[10]He W Q ，Lawless J F.Bivariate Location-Scale Models for Regres⁃sion Analysis,with Applications to Lifetime Data[J].Journal of the Royal Statistical Society,Ser，B,2005,(67).

[11]Jiang J.Linear and Generalized Linear Mixed Models and their Ap⁃plications[M].New York：Springer,2007.

[12]McCullagh P，Nelder J A.Generalized Linear Models(2ndEditon)[M].London:Chapman and Hall,1989.

[13]Breslow N E，Clayton D G.Approximate Inference in Generalized Linear Mixed Models[J].JASA,1993,(88).

[14]Wolfinger R ，O’Connell M.Generalized Linear Mixed Models:a Pseudo-likelihood Approach[J].J.Statistics,Computation simula⁃tion,1993,(48).

[15]Carroll R J ，Ruppert D.Transformation and Weighting in Regres⁃sion[M].London:Chapman and Hall,1988.

[16]Harville D A.Maximum Likelihood Approaches to Variance Compo⁃nent Estimation and to Related Problems[J].Journal of the American Statistical Association,1977,(72).