多气囊平流层浮空器动力学建模及控制

郭宗易，郭建国，周军

（西北工业大学精确制导与控制研究所，陕西西安 710072）

0 引言

平流层浮空器运行在平流层空域内，其独特的特性使得浮空器在通信、遥感观测、运输、监控和军事侦查等方面具有广阔的应用前景，已经成为新一轮的研究热点［1-6］。

文献［7］建立了一般浮空器模型；文献［8］建立了浮空器俯仰角姿态动力学模型，使用离散滑模变结构方法设计控制律，但没有考虑气囊变化；文献［9］建立了浮空器姿态模型，采用自适应滑模神经网络方法，没有考虑气囊运动和质量变化；文献［10］推导了带有升降气囊和质量块的浮空器模型，但没有进行姿态控制。

本文针对平流层浮空器，详细分析了其受力和力矩，建立了带有多气囊的动力学模型方程，并利用积分变结构控制方法设计其控制律。

1 动力学建模

本文的研究工作基于以下三点假设:

（1）浮空器的体积中心与浮力中心重合；

（2）视浮空器和气囊为刚体，忽略其弹性效应；

（3）浮空器所处的空气条件是稳定的，即没有温度、气压等条件的突变。

以上三点假设是合理的，也是目前国内外研究工作中普遍采用的简化方法［8］。

1.1 外力和外力矩

如图1所示，Oxyz为机体坐标系，原点位于浮空器体心O，浮心与体心重合，质心在浮心正下方。

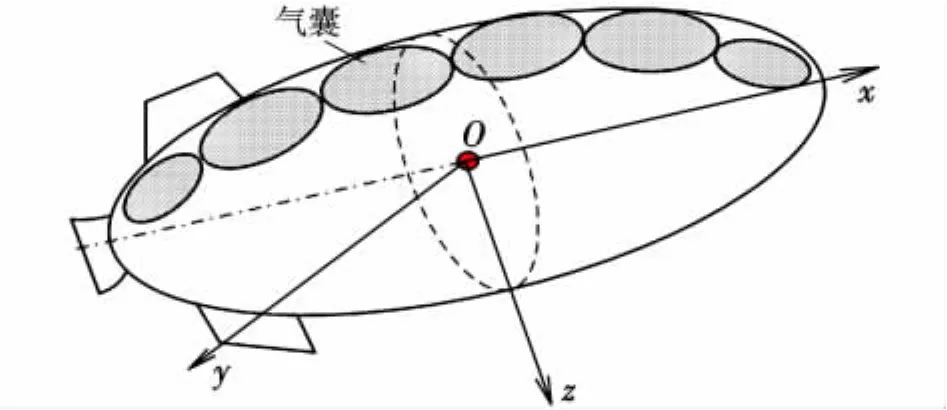
图1 浮空器结构和机体坐标系Fig.1 Structure and body coordinate of airship

在机体坐标系中，浮空器所受总外力FΣ和总外力矩MΣ可表示为:

式中，R1为速度坐标系与机体系之间的转换矩阵；R2为惯性系到机体系的转换矩阵；其他各参数的意义和计算如下:

（1）流体惯性力FI和流体惯性力矩MI

与传统飞行器相比，浮空器具有很大的体积/质量比，在空气中运动时，其惯性特性不能忽略，因此必须考虑其所受的流体惯性力［11］。

浮空器受到的流体惯性力和流体惯性力矩为:

式中，B和K分别为浮空器动量和动量矩；ω=［p，q，r］T为浮空器在机体坐标系中的角速度；V为飞行速度，且V=［u，v，w］T。

（2）气动力FA和气动力矩MA

浮空器受到的空气作用可归并为作用于体心的气动力和气动力矩:

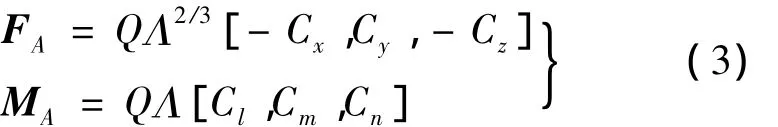
式中，Q=0.5ρV2为动压；ρ为空气密度；Λ为浮空器体积；Cx，Cy，Cz分别为轴向、侧向和法向气动力系数；Cl，Cm，Cn分别为滚转、俯仰和偏航气动力矩系数。

（3）浮力FB和浮力矩MB

浮空器所受浮力由其体积排开的空气产生，即:

式中，g为重力加速度。

浮力作用于机体坐标系原心，不产生力矩，即:

（4）重力FG和重力矩MG

浮空器所受重力为:

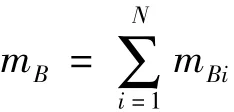
浮空器所受重力矩为:

式中，rJ=［xJ，yJ，zJ］T和rBi（i=1，2，…，N）分别为机体质心和各气囊质心在机体坐标系中的位置向量。

（5）推力FT和推力矩MT

平流层浮空器由直流发动机带动螺旋桨产生推力，其推力与飞行速度和发动机转速有关:

浮空器的发动机沿Ox轴安装于浮空器尾部，推力沿Ox轴方向。所以浮空器所受推力矩为:

1.2 动量和动量矩

在机体坐标系，机体动量为:

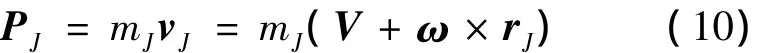
式中，vJ为机体的绝对速度。

浮空器机体的动量矩为:

式中，JJ为机体质量mJ在机体系的惯性矩阵。

在机体坐标系，气囊的动量为:

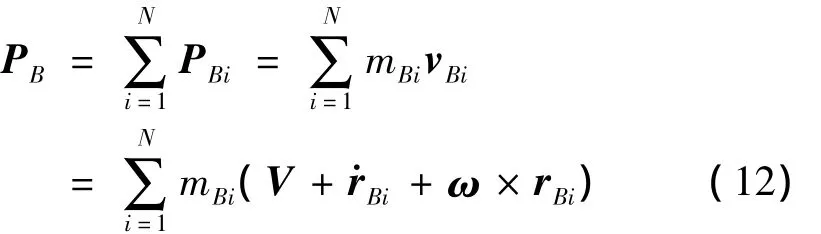
式中，vBi（i=1，2，…，N）为气囊的绝对速度。

气囊的动量矩为:

1.3 动力学模型

浮空器的总动量和动量矩为:

考虑到飞艇升降过程中气囊充放气，所以各气囊质量并不恒定，质心也不断变化。若对式（14）求导则可求得FΣ和MΣ:

综合计算式（10）～式（15），可以得到带有质量块浮空器的动力学方程为:

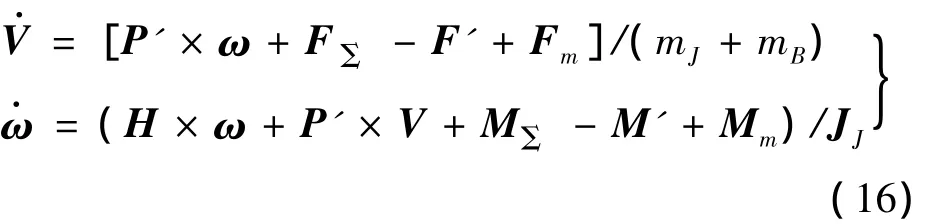
其中:

由式（16）可以看出，力Fm和力矩Mm由气囊的质量变化和非定常运动引起，这是由于带有多气囊的浮空器本质是一个多体系统，内部气囊自身质量变化和运动以及和机体相互作用产生了附加力和附加力矩，这导致浮空器模型变得复杂。如果认为各气囊质量恒定且质心不变，即=0Bi=0，那么模型（16）将变为如文献［12］的普通浮空器模型。

2 控制律设计

考虑俯仰通道模型，那么侧向参数均为零。假设通过合理配置浮空器质量分布，可以保证机体的质心和气囊位置始终在纵向平面内。令:

式中，rB为浮空器所有气囊的平均质心位置。

一般取在某特征点处进行控制律设计，此时u=U0，w=W0，可以得到俯仰通道姿态运动方程:

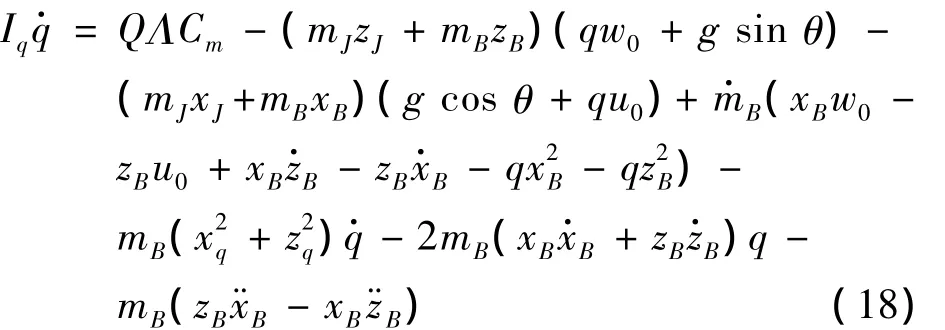
其中:

这里认为D为干扰，实际运动中，气囊运动位移、速度和加速度均有限，所以D有界。

变结构控制方法具有良好的动态性能和强鲁棒性，工程实现容易［13］。所以本文采用此种方法来针对所研究的浮空器姿控模型设计控制律。

定理1:对于如式（19）的系统，如果满足条件

在俯仰舵偏控制律

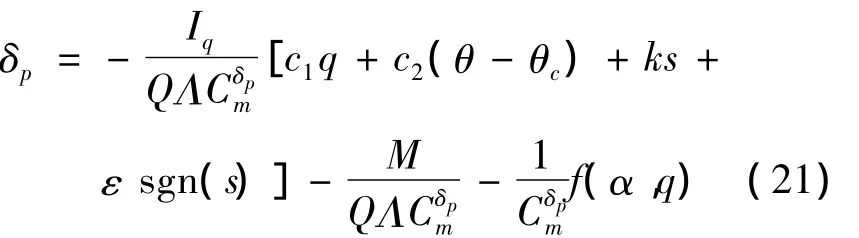
的作用下，系统能够实现对俯仰角指令的稳定跟踪。

证明:设期望俯仰角为θc，那么定义指令跟踪误差e=θ－θc。取滑模超平面

对Lyapunov函数V=s2/2求导得:

代入控制律式（21）和Cm，则有:

只要满足式（20）即有:

式中，k和η为正数，所以＜0，于是由Lyapunov定理可知系统全局渐近稳定。

另一方面，滑模超平面上满足=0，所以对s求导得:

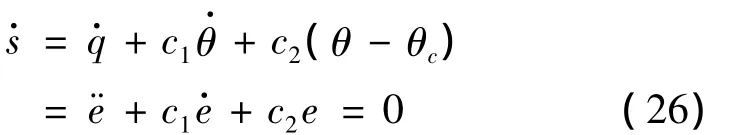
根据霍尔维茨（Hurwitz）准则，可以通过配置c1和c2的值来保证，随着时间t→∞，跟踪误差e→0，实现了控制系统的稳定跟踪。证毕。

注1:对于不加积分项的变结构控制律，一般取其超平面为s=+ce。要获得精确的指令跟踪，必须保证达到s=0平面，而从式（26）的证明可以看出，本文设计的变结构控制律只须使得=0，就可以保证有限时间内跟踪误差的收敛为零。

3 仿真研究

以文献［2］提供的平流层浮空器数据为例:初始俯仰角θ0= －3°；期望俯仰角θc=3°；俯仰舵偏限幅［－20°，20°］；限速率［－20，20］/（°）·s－1；大气密度拉偏范围为－15% ～15%；法向力、轴向力和侧向力系数拉偏范围分别为－15% ～15%，－20% ～20%和－15% ～15%；气动力矩系数拉偏范围为－30%～30%。在Matlab/Simulink环境下进行数字仿真，比较变结构控制律加入积分项前后控制效果，结果如图2～图4所示。

图2 标称情况俯仰角和俯仰舵偏变化曲线Fig.2 Behaviour of pitch angle and rudder in nominal condition

图3 正拉偏情况俯仰角和俯仰舵偏变化曲线Fig.3 Behaviour of pitch angle and rudder in positive condition

图4 负拉偏情况俯仰角和俯仰舵偏变化曲线Fig.4 Behaviour of pitch angle and rudder in negative condition

对以上的仿真结果曲线进行分析可得到以下结论:

（1）控制律加入积分项前，俯仰角调节时间较长，超调量较大，俯仰舵偏变化较剧烈。加入积分项之后，浮空器的姿态在各种情况下，50 s以内均可以收敛到期望的跟踪俯仰角，调节时间较短；标称和负拉偏情况下超调量为零，正拉偏情况超调量很小，动态性能得到很大改善，俯仰舵偏的变化也较为平滑。

（2）仿真考虑了俯仰舵偏的限幅和限速率，在标称和正负拉偏情况下均可以实现俯仰角和俯仰舵偏的快速精确收敛。这说明设计的控制器具有良好的鲁棒性和适应性。

4 结束语

浮空器的动力学方程由于多气囊的运动和质量变化而变得复杂，而本文针对此问题采用积分变结构控制方法，使用Lyapunov理论证明其稳定性，而且通过仿真分析比较了加入积分项前后的控制效果，验证了这种控制律具有良好的鲁棒性和动态性能，而这种控制律会随着我国浮空器技术的进一步发展而获得更大应用。

［1］Ferguson D C，Hillard G B.Paschen considerations for high altitude airships［R］.AIAA-2004-1260，2004.

［2］Mueller J B，Paluszek M A，Zhao Yiyuan，et a1.Development of an aerodynamic model and control law design for a high altitude airship［C］∥AIAA 3rd Unmanned Unlimited Technical Conference，Workshop and Exhibit.Chicago，Illinois，2004:2-17.

［3］Colozza A，Dolce J L.High-altitude，long-endurance airships for coastal surveillance［R］.NASA-TM-2005-213427，2005.

［4］Lambert C.Developing architectures for high altitude airships［R］.AIAA-2003-6781，2003.

［5］Khoury G A，Gillett J D.Airship Technology［M］.UK:Cambridge University Press，1999:28-33.

［6］Griffin D K，Swinyard B M，Sidher，et al.Feasibility study of a stratospheric airship observatory［C］//Proceeding of SPIE.2003:227-238.

［7］Gomes V B，Ramos J G.Airship dynamic modeling for autonomous operation［C］//Proceedings of the 1998 IEEE International Conference on Robotics and Automation.Belgium:IEEE，1998:3462-3467.

［8］方存光，王伟.自主飞艇俯仰角姿态动力学建模及控制［J］.控制理论与应用，2004，21（2）:231-238.

［9］郭建国，周军.基于滑模神经网络的自主飞艇姿态［J］.飞行力学，2009，27（1）:40-42.

［10］Cai Zili，Qu Weidong，Xi Yugeng.Dynamic modeling for airship equipped with ballonets and ballast［J］.Applied Mathematics and Mechanics，2009，26（8）:1072-1082.

［11］Tuckerman L B.Inertia factors of ellipsoids for use in airship design［R］.NACA Report No.210，1925.

［12］Ouyang J.Research on modeling and control of an unmanned airship（in Chinese）［D］.Ph.D.Thesis，Shanghai Jiaotong University，Shanghai，China，2003.

［13］高为炳.变结构控制理论基础［M］.北京:中国科学技术出版社，1998:241-273.