一种计算雷达高度计重跟踪修正表的新方法及其应用

王 磊 许 可 徐曦煜 史灵卫

①(中国科学院微波遥感技术重点实验室 北京 100190)

②(中国科学院空间科学与应用研究中心 北京 100190)

③(中国科学院大学 北京 100049)

1 引言

雷达高度计是海洋动力环境测量的重要仪器。对其观测数据进行处理，可以获得高精度的海面高度、海面有效波高和海面后向散射系数等参数。目前，雷达高度计在海面地形测量，海洋大尺度环流、中尺度洋流和涡流，潮汐，海洋异常观测等方面得到了广泛的研究和应用[1-5]。国际上，以欧美为代表，已发射了TOPEX/Poseidon, Geosat, GFO,ERS-1, ERS-2, Envisat, Jason-1, Jason-2等卫星雷达高度计。我国也于2011年8月16日成功发射了我国第1颗海洋动力环境卫星HY-2，其主载荷之一为雷达高度计[6]。

为了获得高精度的数据处理结果，高度计在卫星上获得观测数据以后，通常都是将数据打包后下传到地面再进行精细的处理。在雷达高度计数据的地面处理流程中，回波重跟踪是关键步骤，它是获得高精度的海面参数的重要保证。回波重跟踪，即采用理论回波模型对实际回波信号进行拟合以提取精确的测量参数。在回波重跟踪时，由于数据量大且准确的高度计回波模型计算复杂，为了提高处理速度，通常采用近似的回波模型对实际回波进行拟合，然后再计算由于模型近似带来的重跟踪误差，并将这一重跟踪误差制作成误差修正表，利用误差修正表对重跟踪结果进行修正[7,8]。

目前已有的计算高度计重跟踪修正表的方法，在计算修正值时将平坦海面脉冲响应函数用指数函数近似表示[7,8]。本文分析了导致雷达高度计回波重跟踪结果产生误差的主要因素，通过仿真分析了将平坦海面脉冲响应函数近似为指数函数对修正表的影响，在此基础上提出了采用平坦海面脉冲响应函数准确形式计算修正表的方法，并采用该方法计算了HY-2卫星雷达高度计的重跟踪修正表，对其数据进行了处理。结果表明，在天线误指向角较大时，采用指数函数近似的平坦海面脉冲响应函数来计算修正值会带来较大的误差，而采用准确的平坦海面脉冲响应函数则可以显著降低这一误差。

2 雷达高度计回波重跟踪修正表

2.1 回波模型中的近似项分析

雷达高度计回波信号随时间变化的函数，即高度计的回波模型，可以表示为3个函数的卷积[9-11]。

式(1)中W(τ)表示雷达高度计回波信号的平均功率，Pfs(τ)是平坦海面的脉冲响应函数，PTR(τ)是高度计系统的点目标响应函数，PDF(τ)是海面散射点的概率密度函数。

散射点的概率密度函数一般用有偏的高斯函数来表示[12-14]。

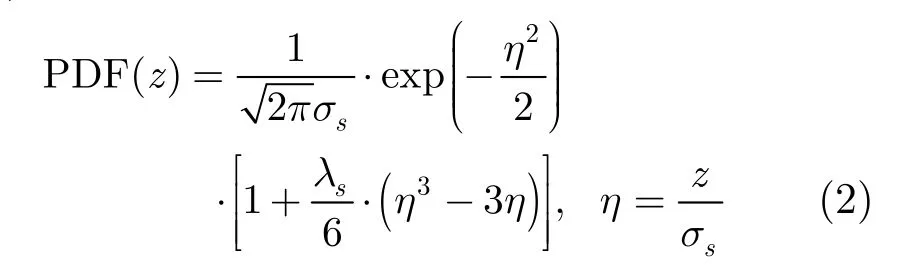
式(2)中，z是散射点距平均海平面的高度，z=0定义为平均海平面，延时与高度的换算关系为τ=-2(z/c);σs是均方根波高，有效波高定义为它的4倍。

高度计系统的理想点目标响应函数是sinc函数的平方：

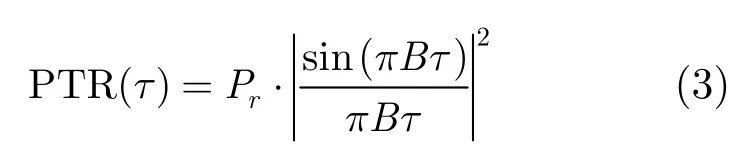
式(3)中B是高度计发射信号的带宽，Pr是一个与高度计系统及发射信号功率有关的常数。高度计硬件系统的实测点目标响应与式(3)描述的理想形式之间会有一定的差别。

平坦海面的脉冲响应函数可表示为[10,11]

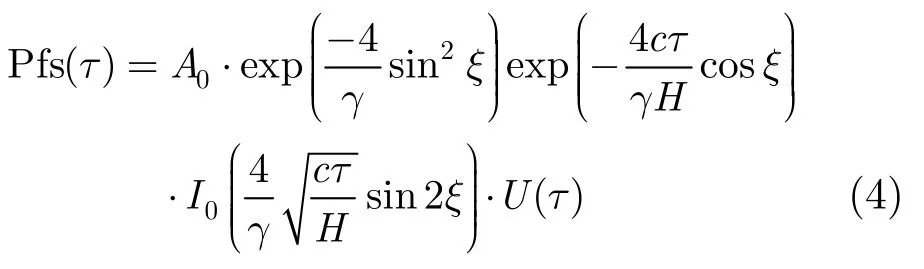
式(4)中I0(·)是第1 类修正的 0阶贝塞尔函数，U(·)是阶跃函数；A0是一个与高度计系统参数及轨道高度H、海面的后向散射系数有关的常量；γ=(2/ln2)·si n2(θw/2),θw是天线主瓣的3 dB波束宽度；ξ是天线指向偏离星下点的角度，即误指向角。

如上所述，在雷达高度计的回波模型中，高度计硬件系统的实测点目标响应无法用明确的数学函数表达，因此不可能得到高度计真实回波模型的解析表达式；同时，平坦海面脉冲响应函数中含有第1类修正的 0阶贝赛尔函数，计算比较复杂。而在实际工程应用中，由于需要处理的数据量很大，若在回波重跟踪时采用式(2)和式(4)及系统的实测点目标响应，然后直接用式(1)计算回波模型将会使得计算量过大而延误数据的时效性。因此通常先采用近似模型对实际回波重跟踪，在重跟踪之后再校正由于模型近似带来的误差。

目前，在高度计回波重跟踪中常用的回波模型是由 Rodgiguez[15]在 Brown[10]和 Hayne[11]的基础上推导出来的，他将系统的点目标响应函数用高斯函数近似为

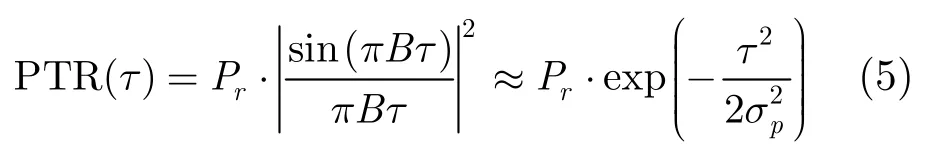
并将式(4)所示的平坦海面脉冲响应函数中的第1类0阶贝赛尔函数用指数函数近似为

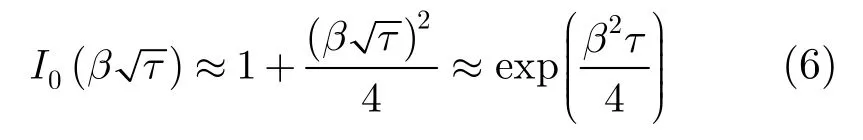
将式(6)代入式(4)，可得平坦海面脉冲响应函数的指数近似形式为

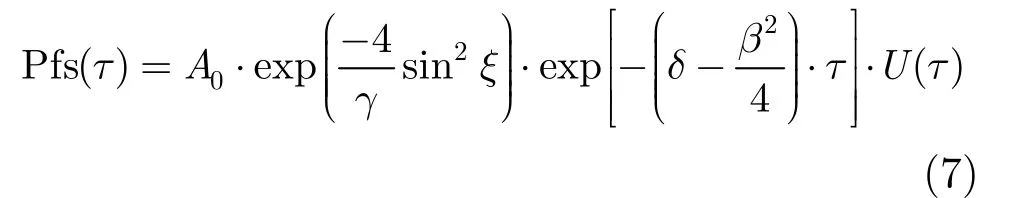
将式(2)，式(5)，式(7)代入式(1)，可得近似回波模型为

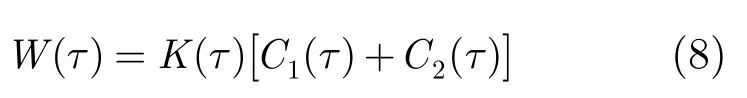
在式(8)中

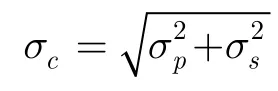
如上所述，Rodgiguez近似模型[15]与准确模型之间存在两方面的误差：平坦海面脉冲响应函数中第1类0阶贝塞尔函数用指数函数近似的误差；高度计系统点目标响应函数用高斯函数近似的误差。因此在计算修正表时，这两个方面都应考虑。

另外，高度计系统的信噪比对修正值也有一定的影响[8]，通过仿真发现，当高度计系统的信噪比从13 dB变化到25 dB时，高度修正值的变化不超过3 mm，有效波高的修正值不超过2 cm，散射系数的修正值几乎不变。高度计在正常工作时的信噪比通常都高于13 dB且稳定性较好，因此信噪比的影响可以忽略不计。

2.2 修正表制作流程

在计算高度计修正表时，海面的有效波高不同，重跟踪结果的修正值不同；天线的误指向角不同时，重跟踪结果的修正值也不同。因此修正表应该是以有效波高和天线误指向角为索引的2维查找表。计算修正值的流程如下：

首先采用平坦海面脉冲响应函数、波高概率密函数及系统实测点目标响应函数，仿真出不同误指向角、不同有效波高下的高度计海面回波，然后采用近似模型对仿真回波进行重跟踪，最后将仿真时设定的参数减去其对应的重跟踪结果，即可得重跟踪结果的修正值。

此外，修正值还与重跟踪算法有关系，重跟踪算法不同修正值也不同，比如采用最小二乘算法和最大似然算法得到的修正值是不一样的。因此，计算修正值的算法与回波重跟踪算法应保持一致。

3 指数函数近似平坦海面脉冲响应函数对修正值的影响

如第2节所示，在计算修正值时，应同时考虑平坦海面脉冲响应函数和高度计系统点目标响应函数这两方面的因素。然而 Hayne等人[7]在计算TOPEX卫星雷达高度计的修正表，及Amarouche等人[8]在计算Jason-1卫星雷达高度计的修正表时，都忽略了平坦海面脉冲响应函数的影响，他们都将平坦海面的脉冲响应函数用指数函数近似表示。

如图 1所示是当误指向角分别为0.2°和 0.7°时，平坦海面脉冲响应函数(Pfs)的准确形式与其指数函数近似形式。从图中可以看出，在误指向角较小时，用指数函数近似平坦海面脉冲响应函数误差较小；但在误指向角较大时两者之间的误差较大，必然会对重跟踪结果的修正值带来较大的误差。

为了确定平坦海面脉冲响应用指数函数近似后对修正值的影响，本文假设高度计系统为理想状况，即其点目标响应为sinc函数平方；波高概率密度函数为式(2)所示的高斯函数；令平坦海面脉冲响应函数分别为其准确形式及指数函数近似形式计算了重跟踪结果的修正表。重跟踪算法采用最小二乘算法，同时估计高度、有效波高、回波幅度和误指向角这4个参数。

图2所示是当海面的有效波高为2 m时，平坦海面脉冲响应函数分别为准确形式和指数函数近似形式时的修正值随指向角的变化趋势。图中，实线(修正值 1)是采用准确形式得到的修正值，虚线(修正值2)是采用指数函数近似形式得到的修正值，点线是两者之差。从图中可以看出，当雷达高度计天线的误指向角较小时(小于 0.2°)，将平坦海面脉冲响应函数近似为指数函数得到的修正值与准确平坦海面脉冲响应函数得到修正值之间的误差较小，但随着误指向角的增大，指数函数近似的平坦海面脉冲响应对修正值带来的误差也随之增大，当误指向角增大到0.7°，高度修正值的误差达到了10 cm，有效波高修正值的误差超过了 50 cm，后向散射系数修正值的误差达到了2 dB，而误指向角修正值的误差超过了0.1°。如此大的误差，对于高度计是不能接受的。

图3所示是当天线的误指向角为0.7度时，近似平坦海面脉冲响应函数和准确平坦海面脉冲响应函数情况下重跟踪结果的修正值随有效波高的变化趋势。图中，实线(修正值1)是采用准确的平坦海面脉冲响应函数得到的修正值，虚线(修正值2)是采用其指数函数近似形式得到的修正值，点线是两者之差。可以看出，在误指向角为0.7°，采用指数函数近似的平坦海面脉冲响应函数得到的修正值与采用准确的平坦海面脉冲响应函数得到的修正值之间的误差随有效波高的变化而变化，其中高度与有效波高修正值的绝对误差随着有效波高的增大而增大；后向散射系数修正值的绝对误差随有效波高的变化很小，基本保持在2 dB左右；误指向角修正值的绝对误差随有效波高的变化也很小，基本保持在0.11°左右。

综合图2和图3可知，在计算修正表时，采用指数函数来近似平坦海面脉冲响应函数，在天线误指向角较小时修正表的误差较小，在误指向角较大时则会带来较大的误差。虽然目前雷达高度计卫星指向精度控制已较高，但仍然难以避免天线出现误指向角较大的情况，比如 Jason-1雷达高度计[16]及HY-2卫星雷达高度计入轨初期都曾出现天线误指向角较大的情况。为了保证在误指向角较大的情况下数据处理的准确性，在计算修正表时，应采用准确的平坦海面脉冲响应函数。

图1 平坦海面脉冲响应函数(Pfs)及其指数近似形式

图2 高度、有效波高、后向散射系数及误指向角的修正值随实际误指向角的变化

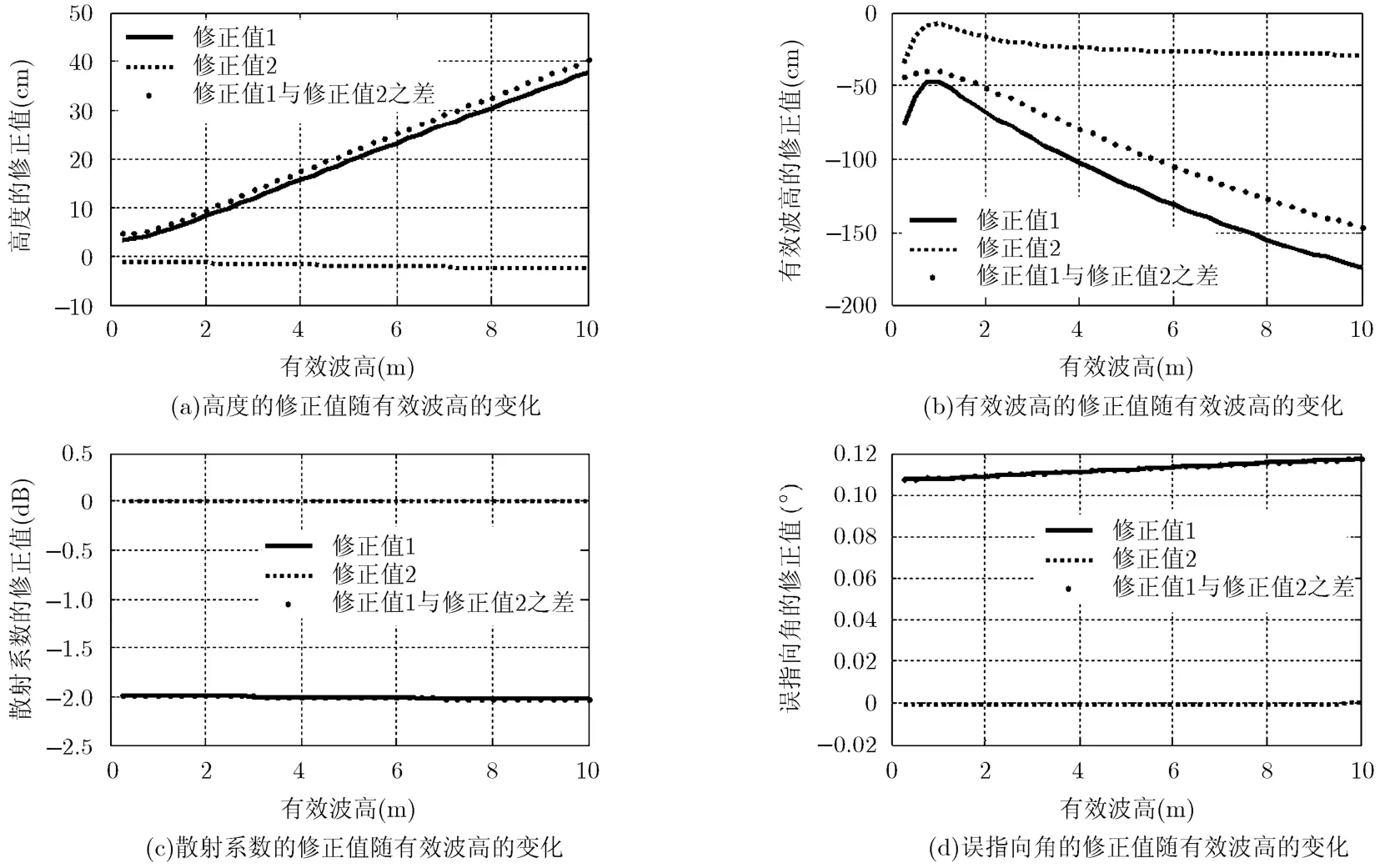
图3 高度、有效波高、后向散射系数及误指向角的修正值随有效波高的变化

4 HY-2卫星雷达高度计的修正表及回波数据处理

2011年8月16日，我国HY-2卫星成功发射，目前已正常运行。在 HY-2卫星刚入轨后的卫星姿态调整期间，雷达高度计天线的误指向角较大，在此阶段雷达高度计也获得了一些数据。为了验证本文的工作内容，本文针对 HY-2卫星雷达高度计计算了其重跟踪修正表并对其回波数据进行了处理。回波重跟踪算法采用最小二乘算法，在算法中同时联合估计高度、有效波高、散射系数和误指向角这4个参数。HY-2卫星雷达高度计与回波重跟踪相关的主要参数见表1。

表1 HY-2卫星雷达高度计主要参数

图4是HY-2卫星雷达高度计系统的实测点目标响应(PTR)、理想点目标响应和用高斯函数(σp=0.513·rt)近似的点目标响应的归一化曲线。从图中可以看出，HY-2卫星的系统点目标响应函数十分接近其理想形式。

本文计算出的 HY-2卫星雷达高度计重跟踪结果的修正表共4张，即高度、有效波高、后向散射系数、误指向角都需校正。每张修正表均以有效波高和误指向角为索引。修正表的制作方法如第2节所述，受篇幅所限，在此不列出修正表的具体内容。

图5(a)所示是HY-2卫星姿态调整正常后，误指向角较小时获得的海面回波及模型拟合结果；图5(b)是在姿态调整期间，误指向角较大时获得的海面回波及模型拟合结果。可以看出，天线误指向角较小时和较大时的回波信号存在很大的差别。

由于调姿阶段的轨道高度没有经过精密定轨，因此无法得到高度计测量海面高度的准确值。为了验证本文的工作内容，本文将高度计回波中反演出的海面有效波高与 NDBC(National Data Buoy Center)海洋浮标的同步观测结果进行了对比。NDBC的每个浮标每小时公布一个有效波高的测量值。高度计数据与浮标数据匹配的空间、时间标准为：高度计足迹与浮标的距离小于50 km，时间间隔小于0.5 h。本文先对匹配区域内的所有回波分别进行重跟踪，然后对重跟踪结果进行1 s平均并用修正表修正，最后对所有 1 s平均并修正过的数据进行统计平均得到最终结果，再与浮标测量结果比较。对误指向角较大时的高度计回波数据处理得到的海面有效波高值与浮标测量值如表2所示。

在表2中，以浮标测量的海面有效波高值为真值，可得采用由平坦海面脉冲响应的指数函数近似形式计算出的修正表修正后的有效波高的标准差为86.3 cm，采用由平坦海面脉冲响应函数准确形式计算的修正表修正后的有效波高的标准差为31.1 cm。可见在误指向角较大的情况下，采用指数函数近似的平坦海面脉冲响应函数计算的修正表误差很大；而采用准确的平坦海面脉冲响应函数计算的修正表误差较小。

表3所列是对HY-2卫星雷达高度计在姿态正常时获得的回波数据处理得到的海面有效波高与浮标测量值。以浮标测量的海面有效波高值为真值，可得采用由平坦海面脉冲响应的指数函数近似形式计算出的修正表修正后的有效波高的标准差为 9.4 cm，采用由平坦海面脉冲响应函数准确形式计算出修正表修正后的有效波高的标准差为9.2 cm。可见在天线误指向角较小的情况下，采用指数函数近似的平坦海面脉冲响应函数计算出的修正表与准确的平坦海面脉冲响应函数计算出的修正表之间的误差很小，都可获得准确的重跟踪结果修正值。

5 结论

图4 不同形式的高度计系统点目标响应

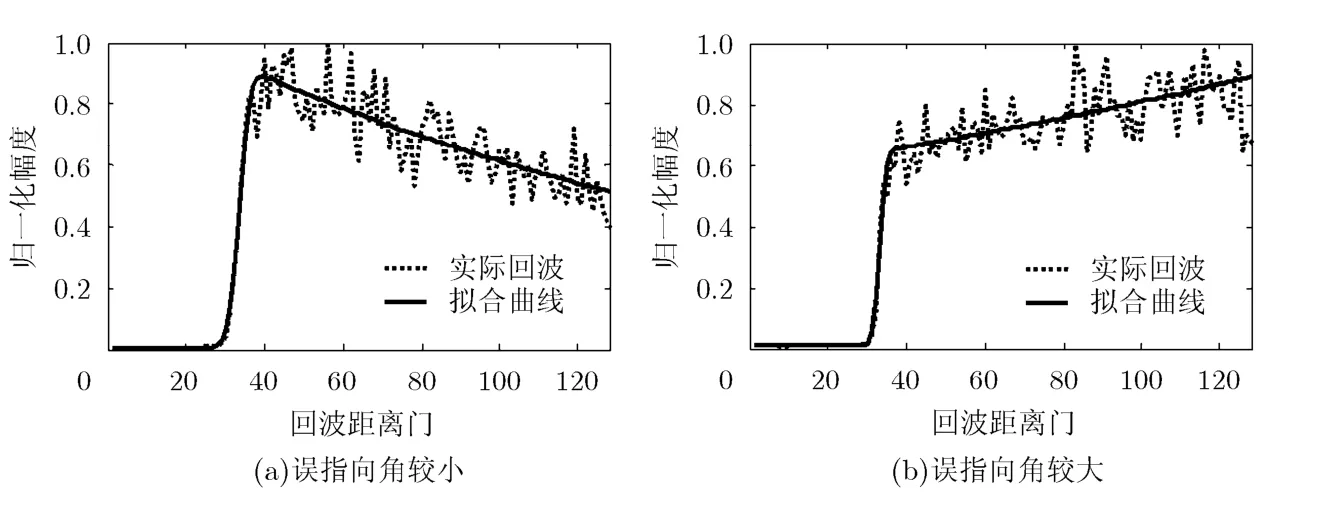
图5 HY-2卫星雷达高度计的典型海面回波及模型拟合回波

表2 高度计数据反演出的有效波高与浮标测量值(反演出误指向角约0.7°)

表3 高度计数据反演出的有效波高与浮标测量值(反演出误指向角小于0.2°)

在高度计回波重跟踪时，为了提高数据处理的速度往往采用近似的回波模型，这种近似对重跟踪结果会带来误差，该误差的校正一般采用查找表的方式。传统的计算修正表的方法，将平坦海面脉冲响应函数近似为指数函数，这样得到的修正表在天线误指向角较小时误差较小，但在天线误指向角较大时则会带来较大的误差。

本文分析了将平坦海面脉冲响应函数近似为指数函数对修正表的影响，提出了采用平坦海面脉冲响应函数准确形式计算重跟踪修正表的方法，并针对 HY-2卫星雷达高度计制作了修正表，对其在姿态调整阶段误指向角较大时获得的数据，以及姿态调整正常后误指向角较小时获得的数据进行了处理。处理结果表明，在误指向角较大时，采用准确平坦海面脉冲响应函数计算修正表可以获得更准确的海面参数。

[1]姜祝辉, 黄思训, 刘刚, 等. 星载雷达高度计反演海面风速进展[J]. 海洋通报, 2011, 30(5): 588-594.

Jiang Zhu-hui, Huang Si-xun, Liu Gang,et al.. Research on the development of surface wind speed retrieval from satellite radar altimeter[J].Marine Science Bulletin, 2011, 30(5):588-594.

[2]Klemas Victor. Remote sensing techniques for studying coastal ecosystems: an overview[J].Journal of Coastal Research, 2011, 27(1): 2-17.

[3]Klemas Victor. Remote sensing of coastal and ocean currents:an overview[J].Journal of Coastal Research, 2012, 28(3):576-586.

[4]Sadatipour S M T, Kiamehr R, Abrehdary M,et al.. The evaluation of sea surface topography models based on the combination of the satellite altimetry and the global geoid models in the Persian Gulf[J].International Journal of Environment Research, 2012, 6(3): 645-652.

[5]Zhang Lin-lin, Sun Che, and Hu Dun-xin. Interannual variability of the Antarctic Circumpolar Current strength based on merged altimeter data[J].Chinese Science Bulletin,2012, 57(16): 2015-2021.

[6]Jiang Xing-wei, Lin Ming-sen, Liu Jian-qiang,et al.. The HY-2 satellite and its preliminary assessment[J].International Journal of Digital Earth, 2012, 5(3): 266-281.

[7]Hayne G S, Hancock D W, Purdy C L,et al.. The corrections for significant wave height and attitude effects in the TOPEX radar altimeter[J].Journal of Geophysical Research, 1994,99(C12): 24941-24955.

[8]Thibaut P, Amarouche L, and Zanife O Z. Jason-1 altimeter ground processing look up correction tables[J].Marine Geodesy, 2004, 27(3/4): 409-431.

[9]Moore R K and Williams C S. Radar terrain return at near vertical incidence[J].Proceedings of The IRE, 1957, 45(2):228-238.

[10]Brown G S. The average impulse response of a rough surface and its application[J].IEEETransactions on Antennas and Propagation, 1977, 25(1): 67-74.

[11]Hayne G S. Radar altimeter mean return waveforms from near normal incidence ocean surface scattering[J].IEEE Transactions on Antennas and Propagation, 1980, 28(5):687-692.

[12]Srokosz M A. On the joint distribution of surface elevation and slopes for a nonlinear random sea, with an application to radar altimetry[J].Journal of Geophysical Research, 1986,91(C1): 995-1006.

[13]Tokmakian R T, Challenor P G, Guymer T H,et al.. The U.K.EODC ERS-1 altimeter oceans processing scheme[J].International Journal of Remote Sensing, 1994, 15(4):939-962.

[14]Gomez Enri J, Gommenginger C P, Srokosz M A,et al..Measuring global ocean wave skewness by retracking RA-2 Envisat waveforms[J].Journal of Atmospheric and Oceanic Technology, 2007, 24(6): 1102-1116.

[15]Rodriguez E. Altimetry for non-Gaussian oceans: height biases and estimation of parameters[J].Journal of Geophysical Research, 1988, 93(C11): 14107-14120.

[16]Amarouch L, Thibaut P, Zanife O Z,et al.. Improving the Jason-1 ground retracking to better account for attitude effects[J].Marine Geodesy, 2004, 27(1/2): 171-197.