基于差分演化算法的自适应无迹卡尔曼滤波

金 瑶 蔡之华 梁丁文

(中国地质大学(武汉)计算机学院 武汉 430074)

1 引言

在离散时间随机动态系统状态估计问题中，应用了大量的滤波技术。线性系统中一般是用贝叶斯递推关系计算条件状态的概率密度函数，从概率密度函数中获取详细的系统状态估计信息，从而进行准确的估计[1]。其中最著名的是Kalman滤波——线性高斯系统下的最优滤波。而非线性滤波系统的状态估计一般采取次优的近似方法。一种方法是将非线性环节线性化处理，对高阶项逼近或截断，其中最常用的是扩展卡尔曼滤波(Extended Kalman Filter, EKF)[2]。另一种方法是用采样方法近似非线性函数的概率密度分布，常用的有粒子滤波器(Partial Filter, PF)[3]、无迹卡尔曼滤波(Unscented Kalman Filter, UKF)[4]。

EKF将非线性函数的 Taylor展开式中高阶项截断，但是截断的高阶项必然会造成误差。此外，EKF计算过程中需要计算非线性函数的 Jacobi矩阵，计算过程复杂且可能无解，这些问题限制了EKF的应用。PF使用参考分布，随机产生大量粒子，由系统定义的非线性函数将这些粒子转换后通过策略统计组合得到系统估值，PF虽然克服了EKF的缺点但近似过程需要生成数量庞大的粒子，在高维问题中计算量很大；此外粒子在迭代后产生退化问题，也影响了滤波精度[5]。UKF与PF一样也应用采样策略近似非线性分布的方法，不同之处在于UKF用无迹变换(Unscented Transformation, UT)进行确定性采样而非随机采样。UT通过一组能够伸缩且确定数目的Sigma点，计算其均值与协方差近似系统状态。UKF的计算量基本与EKF相当，但性能优于EKF；由于采用的是确定性采样，也避免了PF的粒子退化问题[5]。

由于 UKF在解决某些应用问题时性能要明显优于EKF与PF，对UKF算法的研究与改进也一直是非线性随机动态系统状态估计研究的热点。文献[6]对Sigma点采样策略进行改进，减少了Sigma点数量，在高维问题计算中能显著提高计算效率。文献[7]对 UKF噪声处理方式进行改进，提出了增广UKF，将系统噪声与观测噪声加到状态变量的协方差中，扩维后经过UT过程能处理非累加性噪声，提高滤波精度。文献[8]由新息和残差的正交性原理估计过程噪声协方差的实时变化，利用协方差匹配原则修正噪声理论协方差以逼近真实噪声，提出一种基于新息和残差序列在线估计噪声统计特性的自适应UKF。文献[9]根据极大后验估计原理，推导出一种次优无偏极大后验估计常值噪声统计估计器；采用指数加权的方法给出时变噪声统计估计器递推公式得到带噪声统计估计器的自适应UKF。

对UKF算法的改进很多，但主要集中在应用研究，对UT变换的理论分析研究与创新相对较少。UT变换最明显的特点是具有缩放能力的采样点，缩放参数控制采样点的分布并影响近似准确性。虽然UT变换对非线性状态后验分布近似达到二阶，但同时也引进了额外的高阶项，若选择合适的缩放参数可以使这些高阶项更加近似真实情况；相反不合适的缩放参数会大幅降低UKF精度甚至发散，即缩放参数的选择增加了UKF性能的不确定性[10]。文献[6]给出了常规的缩放参数选择方法，但实际应用时效果并不理想，仍需要使用者根据实际问题设定才能获得理想的滤波精度。目前针对UKF缩放参数的讨论并不多，因此本文将主要讨论缩放参数选择方法，并结合差分演化算法对其进行优化，提出基于差分演化算法的自适应缩放参数的UKF。本文第2节介绍无迹变换；第3节对一些缩放参数自适应方法进行分析；第4节提出基于差分演化算法的自适应缩放参数的UKF算法并进行仿真实验；第5节进行总结。

2 无迹变换

一个非线性动态系统可以描述为

UKF通过一组带有权重的 Sigma点近似模拟非线性函数随机变量分布，Sigma点计算方法就是通过 UT变换。UT变换在给定采样均值与协方差后，通过特定方法生成一组Sigma点并赋予权重，将所有Sigma点通过非线性转换，将转换后的统计值作为估计值。

Sigma点计算方法为

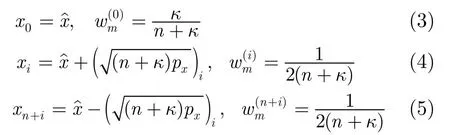
其中i=1,…,n,x0为中心Sigma点，xi是以x0为中心对称分布的Sigma点，为Sigma点均值，px为协方差，n为状态变量维数，wm为Sigma点权重，κ为缩放参数。UT变换共生成2n+1个Sigma点，权重和为1。将Sigma点通过非线性函数yi=h(xi)转换，计算转换后的统计特征。

3 缩放参数选择方法分析

UT变换过程中Sigma点采样策略非常重要，决定了非线性函数近似的效果。在对称采样式(3)-式(5)中，缩放参数κ决定了Sigma点的个数、大小与权重，调节Sigma点与均值点的距离，下面讨论几种κ取值方法。

3.1 常规的缩放参数选择方法

文献[4]就κ值的选择进行了分析，κ变化仅影响二阶之后高阶矩带来的偏差，对于高斯分布，κ取值满足n+κ=3 时可使近似误差控制在四阶矩；当系统维数大于 3时，κ为负值可能导致协方差失去正定性，式(4)，式(5)无法求取平方根导致滤波发散[10]。由此给出了一种κ值选择框架。

当系统维数小于3时，Sigma点分布范围与权重方式固定。当系统维数大于3时，κ只有0一种取值方法，Sigma点分布范围随系统维数增加而扩大相应权重减小。这种取值方法简单被广泛应用，κ为整数由系统维数决定。常规方法实际效果如何，κ取值对滤波精度有怎样的影响，下面通过实验来说明。以Bearings-Only Tracking(BOT)[12]模型为例，用不同κ值的 UKF对其进行滤波处理对比误差。BOT模型定义为

表 1列出了κ取 13个参数进行 100次试验后MSE计算结果。从表1结果看，常规取值方法κ=1时滤波精度并不理想，κ＞1时滤波精度提高，在本次试验中κ=3.5时滤波精度最高。另随机抽取 10组单次试验数据分析发现，13个参数都有可能取得较高的滤波精度MSE小于2，也有可能使滤波发散MSE大于20，并且κ变化会引起滤波MSE很大的波动，说明κ对滤波精度有较大影响，滤波精度对κ选择非常敏感。将上述BOT模型扩展到4维，进行同样的实验也得到了类似的结果。表2列出了在4维系统中不同κ取值的滤波MSE。实验结果显示在4维系统中UKF精度要明显低于2维系统，由常规方法κ=0得到的滤波误差较大，当κ大于2后滤波精度提高。由此可见按照常规方法选择的κ效果并不理想，κ设置更大值时可能提高滤波精度。由于UT变换过程中引进了额外的高阶项， 3n+κ=的条件只是在保证四阶矩近似误差最小情况下获得，并不能保证UT变换对高于四阶矩的近似误差最小[10]。这种取值方法限制了Sigma点的分布与权重可能降低非线性近似效果，实验也证明当κ增大时，扩大Sigma点分布范围有利于提高非线性函数概率密度分布的近似度。

通过上述2维及4维BOT系统应用不同κ进行UKF的实验，可以得出结论：κ设置对UKF精度有较大影响，κ=3-n的固定取值方法并不合适。在κ≥0保证协方差正定性前提下，κ应根据当前时刻估计均值与协方差适时调整才能有效提高滤波精度。另外，κ变化幅度对滤波精度也有较大影响，很小的变化可能导致滤波误差增大甚至发散，滤波精度对κ设置非常敏感。因此需要研究一种新的参数取值方法动态调节κ，降低滤波误差并避免发散。

3.2 其他的缩放参数取值方法

为了提高κ的自适应调整能力，文献[13]通过实验表明κ取值变化比率与UKF精度有较大联系，提出了一种判别式学习方法。通过一组先验实验数据用判别学习方法训练κ，判别方法是以滤波精度是否提高对κ进行定量增减处理。这种学习判别方法原理简单便于实现，但缺点也很明显。首先必须准备大量与模型对应的准确的先验数据作为判别标准，κ优化效果取决于训练数据规模。当模型参数变化后又需要新的训练数据，应用时很不方便。此外滤波精度对κ变化十分敏感，κ变化幅度难以控制。学习判别过程需要花费大量时间，算法效率不高不便广泛应用。

表1 2维系统κ不同取值UKF MSE计算结果

表2 4维系统κ不同取值UKF MSE计算结果

文献[1]通过对 UKF误差分析得出结论，κ=3-n是用缩放参数消除四阶项和最直接的方式，但实际上UT过程中引入的高阶项可能产生更大的误差，这仅是一种先验参考方法[1]。然后提出了一种自适应取值方法，定义以κ为参数的每时刻状态预测估计的近似似然函数为

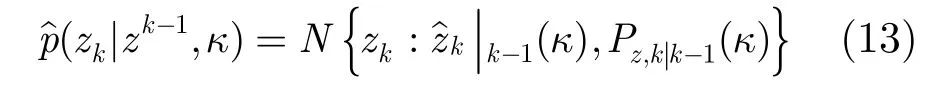
由观测值zk计算最合适的κ值：

似然函数由高斯概率密度函数近似获得。应用网格方法或随机搜索的方法对κ进行选择，指定范围κ∈[0,9n]。κ最大值为9n是为了使非中心的Sigma点权重和最小为0.1，避免这些Sigma点因权重太小被忽略[1]。

这种方法要优于文献[13]提出的判别式学习方法。使用释然函数作为κ选择标准无需先验数据具有较强实用性。但应用网格搜索方法并未解决κ难以调节的问题，且效率不高。网格法与文献[13]的定量变化方法类似，κ取值范围与网格密度相关，在有限个数的候选解中择优选择。滤波精度提升只是当前网格密度下最优。网格稀疏时κ候选解较少，滤波精度提升有限；网格密集时κ候选解过多，则计算耗时更长。如何平衡网格密度与滤波精度又成为新的问题。此外这种方法只能对κ一个参数进行优化，仅适用于常规的UKF，无法处理需要3个参数的Scaled UKF。

4 基于差分演化算法的自适应UKF

4.1 差分演化算法

上述介绍的两种优化方法中κ变化幅度人为指定，这限制了κ取值精度，而且κ的选择方法效率不高。观察整个UKF过程，可以将κ选择看作一个参数优化问题，优化评价标准为滤波精度。这样便可以使用启发式优化方法对κ优化选择达到自适应的效果。差分演化算法(Differential Evolution,DE)[14]正是这样一种基于种群中样本差异的全局优化算法，具有算法简单、收敛速度快、鲁棒性高、参数易设置等特点，在约束优化计算、聚类计算、非线性优化控制、神经网络优化、滤波器设计等其它方面得到广泛应用[14]。

DE采用实数编码，其原理与遗传算法相似，在给定值域内生成NP个随机样本，对种群内各个样本进行变异、交叉、选择操作。变异操作通过随机选取种群两个不同个体，利用个体间差分向量对个体进行扰动，实现个体变异[15]。DE利用群体分布特性使其具有优秀的搜索能力，迅速确定目标优化值域；交叉操作使个体基因延续至下一代，保持种群多样性；选择操作采用贪婪算法选择更优秀的个体进入下一代种群，使优化对象不断改善[16]。用 DE对κ进行优化，相当于在给定范围内κ有无限个候选解。而 DE优秀的搜索能力使κ调节更自由，能够解决滤波精度对κ选择敏感的问题。

4.2 基于差分演化的自适应无迹卡尔曼滤波

本文将DE与UKF结合，提出一种基于差分演化的UKF缩放参数自适应策略，并应用到滤波计算中。用DE优化UKF的缩放参数κ，利用DE高效的勘探与开采能力，在给定κ值范围内进行寻优处理，以滤波MSE作为DE评价函数，选择使滤波误差最小的κ。在每次滤波计算中根据当前时刻Sigma点均值与协方差对κ进行独立的 DE操作得到经优化选择的κ，其滤波值作为当前时刻滤波结果。将每次滤波计算视为单独的优化问题，贯穿整个滤波过程。基于差分演化的自适应缩放参数UKF的计算步骤为：

步骤 2 由DE对k时刻的UKF的Sigma点缩放参数进行差分演化计算，在给定缩放参数范围内进行种群初始化、变异、交叉、选择操作，完成G代演化过程或到达到中止条件后中止演化。将演化得到最优κk的滤波计算结果作为当前时刻滤波结果。

步骤 3k=k+1，重复步骤2，直到滤波过程结束。

本文提出的自适应策略与文献[1]提出的方法相比，前者用每时刻最小滤波误差作为κ的评价标准比后者用每时刻测量值的近似似然函数为评价标准对滤波精度提升更直接。DE全局随机搜索能力比网格法更强，κ选择更自由有助于提升滤波精度。此外提出新策略不受参数个数的限制，能处理缩放UKF算法。

4.3 仿真实验

表3给出了两种方法在2维，4维系统中滤波MSE与Vc结果，基于DE的自适应UKF精度比使用固定缩放参数的UKF有大幅提升，在4维系统中更为明显。图 1为κ取定值与自适应时滤波误差对比，用 DE选择κ后每时刻滤波误差均不同程度降低，表明这种策略是有效的。在使用固定κ时，Sigma点分布范围与权重固定，可能在某时刻因为误差引起滤波发散降低滤波精度。图2为在2维系统单次试验中的X1模拟效果，固定参数UKF出现了滤波发散的现象。而基于DE的自适应UKF由于κ实时调整，滤波值能始终贴近真实值滤波没有发散。

图 3为这种自适应策略优化后缩放参数κ随时间变化的分布图。κ在整个值域内都有分布，在极值两端区域分布较密集。图3结果表明在非线性滤波状态估计这样的动态系统中，使用固定的参数并不合适，需要实时调节才能提高滤波精度并避免发散，但κ整体分布随意且毫无规律，难以用数学公式进行描述。将κ取值范围扩大设κ∈[0,30]进行实验，优化后κ分布也是同样的现象，值域内分布随意两端密集。但滤波MSE略微增大，因为更大的值域使κ有更多的选择，但增加了 DE的负荷，可能在设定的最大演化代数结束时还未收敛而影响滤波精度。

缩放UKF应用SUT，应用比例修正的方法需要3个参数，文献[5]介绍了一种SUT伸缩参数取值方法：α∈[0,1],β=2,κ=3-n或0。用DE分别对3个参数进行组合优化，并与固定缩放参数缩放UKF进行对比。在2维BOT系统中进行100次独立试验结果如表4。

表4说明在缩放UKF自适应策略同样有效，滤波精度提升明显，并且优化后缩放UKF精度略高于单参数的UKF。观察对3个参数组合优化后的结果，当β=2时对α,κ优化后滤波误差最小，滤波精度高于其它单个或多个参数组合优化的结果。说明在等比例采样方式中β=2是合适的设定，验证了文献[11]提出的高斯分布时β=2是 SUT最佳设定的结论。单独对另两个参数优化结果显示对α优化后MSE低于对κ优化后的MSE，优先对α优化对滤波提升更明显。因此设β=2，对α和κ优化或只对α优化是最佳组合且能提高效率。在上述实验中固定参数的缩放UKF也出现了随机发散现象，而自适应缩放UKF则未发散。

5 结束语

本文介绍并讨论了无迹变换Sigma点缩放参数的取值问题，结合差分演化思想提出了一种基于差分演化算法的自适应缩放参数取值策略：利用 DE调整无迹变换缩放参数，优化Sigma点分布以提高非线性近似效果，并应用到UKF计算中。通过实验表明新策略使用后，不仅有效提高了UKF精度，而且能避免UKF随机波动。但这种后验优化方式无法解释缩放参数选择的依据，优化后的缩放参数分布具有很强随机性难以总结规律。对UKF缩放参数取值方法还需进行深入的研究，下一步考虑引入支持向量回归技术，将滤波估计均值、协方差，新息等内容作为变量因素，用DE优化后的缩放参数作为训练数据，用支持向量回归技术指导UKF缩放参数取值。

表3 固定参数UKF与本文提出的自适应UKF的MSE与Vc对比

图1 固定参数与自适应参数MSE对比

图2 X1模拟图

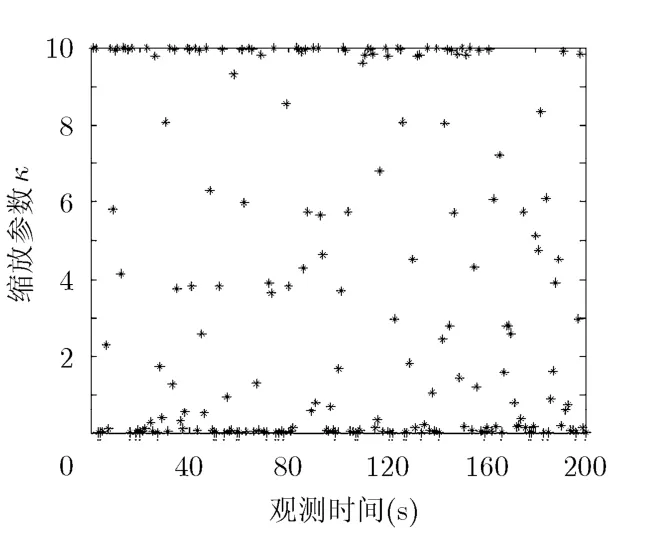
图3 基于DE的自适应缩放参数分布

表4 缩放UKF自适应参数与固定参数MSE与Vc对比

[1]Dunik J, Simandl M, and Straka O. Unscented Kalman Filter:aspects and adaptive setting of scaling parameter[J].IEEE Transactions on Automatic Control, 2012, 57(9): 2411-2416.

[2]Gustafsson F and Hendeby G. Some relations between extended and unscented Kalman filters[J].IEEE Transactions on Signal Processing, 2012, 60(2): 545-555.

[3]Wu Xin-jie and Huang Guo-xing. Application of particle filter algorithm in nonlinear constraint optimization problems[C].2012 8th International Conference on Natural Computation,Chongqing, 2012: 822-826.

[4]Julier S J, Uhlmann J K, and Durrant-White H F. A new method for the nonlinear transformation of means and covariance in filters and estimators[J].IEEE Transactions on Automatic Control, 2000, 45(3): 477-482.

[5]潘泉, 杨峰, 叶亮, 等. 一类非线性滤波器—UKF综述[J]. 控制与决策, 2005, 20(5): 481-489.

Pan Quan, Yang Feng, Ye Liang,et al.. Survey of a kind of nonlinear filters— UKF[J].Control and Decision, 2005, 20(5):481-489.

[6]Julier S J and Uhlmann J K. Reduced sigma point filters for the propagation of means and covariances through nonlinear transformations[C]. American Control Conference, Alaska,2002: 887-892.

[7]Wu Yuan-xin, Hu De-wen, Wu Mei-ping,et al.. Unscented Kalman filtering for additive noise case: augmented versus no augmented[J].IEEE Signal Processing Letters, 2005, 12(5):357-360.

[8]周卫东, 乔相伟, 吉宇人, 等. 基于新息和残差的自适应UKF算法[J]. 宇航学报, 2010, 31(7): 1798-1804.

Zhou Wei-dong, Qiao Xiang-wei, Ji Yu-ren,et al.. An innovation and residual-based adaptive UKF algorithm[J].Journal of Astronautics, 2010, 31(7): 1798-1804.

[9]赵琳, 王小旭, 孙明, 等. 基于极大后验估计和指数加权的自适应UKF滤波算法[J]. 自动化学报, 2010, 36(7): 1007-1019.

Zhao Lin, Wang Xiao-xu, Sun Ming,et al.. Adaptive UKF filtering algorithm based on maximum a posterior estimation and exponential weighting[J].Acta Automatica Sinica, 2010,36(7): 1007-1019.

[10]王小旭, 潘泉, 黄鹤, 等. 非线性系统确定采样型滤波算法综述[J]. 控制与决策, 2012, 27(6): 801-812.

Wang Xiao-xu, Pan Quan, Huang He,et al.. Overview of deterministic sampling filtering algorithms for nonlinear system[J].Control and Decision, 2012, 27(6): 801-812.

[11]Julie S J. The scaled unscented transformation[C]. American Control Conference, Alaska, American, 2002, 6: 4555-4559.

[12]Su Xiao-jing, Yan Jin, and Yan She-feng. A UKF algorithm with two arrays in bearings-only tracking [C]. 2011 4th International Congress on Image and Signal Processing,Shanghai, 2011, 5: 2709-2712.

[13]Sakai A and Kuroda Y. Discriminatively trained unscented Kalman filter for mobile robot localization[J].Journal of Advanced Research in Mechanical Engineering, 2002, 1(3):153-161.

[14]Chakraborty U K. Advances in Differential Evolution[M].Berlin: Heidelberg, Springer-Verlag, 2008: 1-27.

[15]杨启文, 蔡亮, 薛云灿. 差分进化算法综述[J]. 模式识别与人工智能, 2008, 21(4): 506-511.

Yang Qi-wen, Cai Liang, and Xue Yun-can. A survey of differential evolution algorithms[J].Pattern Recognition and Artificial Intelligence, 2008, 21(4): 506-511.

[16]李红伟, 王俊, 王海涛. 一种基于差分演化的粒子滤波算法[J].电子与信息学报, 2011, 33(7): 1639-1643.

Li Hong-wei, Wang Jun, and Wang Hai-tao. A new particle filter based on differential evolution method[J].Journal of Electronics&Information Technogy, 2011, 33(7): 1639-1643.