Molecular Dynamics Simulation of Heterogeneous Nucleation of Argon Vapor onto a Spherical Solid Particle
2013-07-25SONGFenHongLIUChaoZHOUXuan
SONG Fen-Hong LIU Chao,* ZHOU Xuan
(1Key Laboratory of Low-Grade Energy Utilization Technologies and Systems of Ministry of Education,College of Power Engineering,Chongqing University,Chongqing 400030,P.R.China; 2Department of Mechanical Engineering,University of Michigan-Dearborn,Dearborn,MI 48128,USA)
1 lntroduction
Nucleation,which is the first step in a phase transition where clusters form from the supersaturated systems,occurs in numerous natural phenomena and industrial processes,such as condensation,boiling,crystallization and so on.In recent years,a large number of experiments and theoretical studies about melting of solids have greatly enhanced the understanding of the metal nucleation phenomenon.1-5In addition to the cooling and heating rates,6-8the specific surface area,surface roughness,and surface orientation of these nanoparticles have great effect on these condensations and nucleations.9-12The heterogeneous nucleation with already-existent nuclei(foreign material)is much more frequently observed in microelectronics,13nanotechnology,14especially in the atmospheric and geological processes.In the atmosphere,for example,pollutant aerosol particles and dust serve as the cloud condensation nuclei.15,16
The theory of the heterogeneous nucleation of vapor on a solid surface was first proposed in 1958.17Subsequently,a heterogeneous nucleation of a vapor bubble and a liquid droplet on a solid surface was examined by molecular dynamics(MD)simulation,respectively.18,19Additionally,Rżyskoet al.20investigated the nucleation phenomenon of fluids confined in the slit-like pores.In these studies,the bulk surface acts as the heterogeneous nucleation nucleus.Therefore,up to now the general principles of the heterogeneous nucleation on a bulk surface are relatively mature.21While an important characteristic of the atmosphere is the ubiquitous presence of solid particles.When the sulfuric acid or any organic acids condense on one of these solid particles in sufficient quantity,the heterogeneous nucleation will emerge.22However,little is known about the details of how this nucleation process changes when the heterogeneity becomes microscopic scale.Understanding the details of the heterogeneous nucleation is crucial at the micro-level.
Lazaridiset al.23studied the effect of the surface roughness of the solid atmospheric aerosol particles on their heterogeneous nucleation capability,and found that roughness is important to enhance the wetting and rate of heterogeneous nucleation.An experiment24was conducted about an organic vapor(n-propanol)condensing on small clusters,charged and uncharged nanoparticles.The experimental result shows that nucleation occurs at the supersaturation well below that predicted by classical nucleation theory(CNT).25,26It indicates that small particles are much better for the activation nucleation.Inci and Bowels27studied heterogeneous nucleation by adding heterogeneity seed in the same size with vapor particles.
In order to examine the heterogeneous nucleation occurring in the atmosphere at the atomic level,we proposed a novel model that the pre-existing heterogeneous nucleus is represented by a solid nanoparticle in size of a few times larger than that of atoms of nucleation substance.28In this work,we are mainly concerned with the different effects of the cooling rate on the homogeneous and heterogeneous nucleation processes based on our proposed model by directly molecular dynamics simulation,which provides a useful tool for the microscopic studies.29-35In particular,we are further interested in recovering the microscopic dynamic properties of the heterogeneous nucleation of a supersaturated vapor onto a solid nanoparticle.
2 Simulation method
In this paper,a system(shown in Fig.1)was established to simulate the heterogeneous nucleation,in which a spherical solid nanoparticle consisting of 200 Pt atoms acts as the pre-existing nucleus and 5000 Ar atoms as the condensation vapor.The classical Lennard-Jones(LJ)12-636,37potential function was employed to describe the interaction between vapor atoms as following,
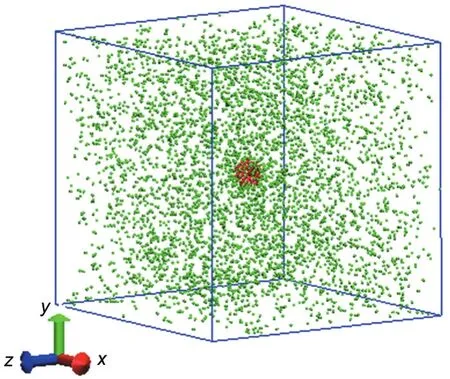
Fig.1 Schematic plot of the simulation system

whereφis the potential energy,rijis the interatomic distance,σandεare the length and energy parameters,respectively.
In order to calculated the potential energy between Ar and Pt atoms,a modified LJ potential function38was used
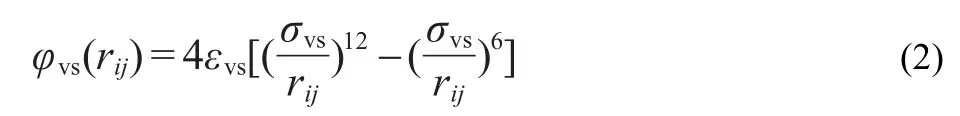
here,v represents vapor,s represents solid.σvsandεvsare the mixed length and energy parameters.These values can be determined by using the Lorentz-Berthelot mixing rule,39
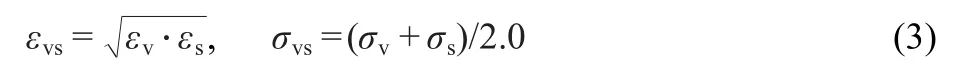
The corresponding potential parameters are listed in Table 1.
The size of the simulation box is 20.5 nm×20.5 nm×20.5 nm.At the start of the simulation,initial velocities of each atom were randomly assigned according to the system temperature of 155.8 K.At this temperature,the system state was above the bimodal(liquid-vapor coexistence)line.40Periodic boundary conditions were applied in all three directions.Newtown's motion equations were solved by the velocity-verlet algorithm41and the time step was set as 5 fs.The Nose-Hoover thermostat(NHT)method42was used to keep the system at the desired temperature at every time step.100000 time steps were run to achieve an equilibrium state.Then,the system temperature was reduced gradually by removing some heat from the system.This removal heat per unit time is defined as the cooling rate,denoted byq.Thus the scale factor of each atom velocity,η,changes to

wherekeis the kinetic energy of all atoms within the system.This method is different from the traditional temperature quenching technique,40and Fig.2 gives the time dependence of temperature distribution for these two methods.It can be seen that the heat removal method can dramatically reduce the disturbance of the system.
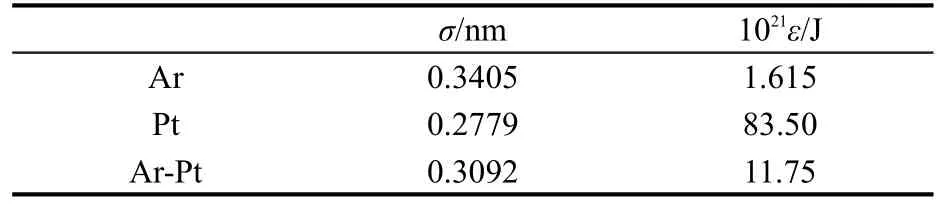
Table 1 Potential parameters adopted in the simulation
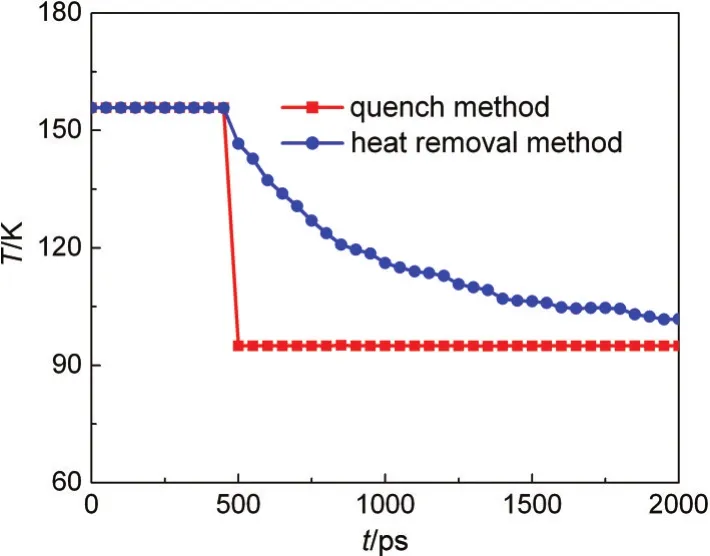
Fig.2 Temperature profiles for two cooling methods
Upon removing heat from the system,data were recorded every 1000 time steps for post-simulation analysis.The total simulation time steps are 1600000.In the work,a cluster during the nucleation process is defined as a interconnecting collection of atoms(at least five atoms)43and whose interatomic distance is less than 1.5σ.Hereσis the length parameter of Ar atom.
3 Results and discussion
3.1 Snapshots of the heterogeneous and homogeneous nucleation
In order to gain a better insight of the heterogeneous nucleation phenomenon,homogeneous nucleation is also investigated with the same initial condition and cooling rate.The evolution of two nucleation processes is depicted in Fig.3 at the cooling rate of 1.50×10-9J·s-1.In the heterogeneous nucleation,argon atoms nucleate on the solid particle to form a larger cluster,and the heterogeneous cluster generated keeps growing(seen in Fig.3(a1,b1)).At the instant of 4000 and 8000 ps,the radii of this cluster are about 2 and 4 nm,respectively.However,in the homogeneous nucleation clusters of various sizes appear and distribute randomly.Some clusters keep growing or disappear or some new clusters form.At 4000 ps four large clusters can survive in the system,and at 8000 ps the largest cluster consists of about 700 atoms as shown in Fig.3(a2,b2).However,the largest cluster is not located in the centre of the simulation box.The reason is that the homogenous nuclei formed by the atoms same as the vapor atoms randomly form and distribute.Additionally,at the instant of 8000 ps the vapor density and the cluster size are almost the same for two systems.It implies that the pre-existing nucleus in the heterogeneous nucleation plays a more important role at the beginning of nucleating(<4000 ps)and then its effect becomes ignorable.The detailed discussion will be given in the following section.
3.2 Temperature profiles
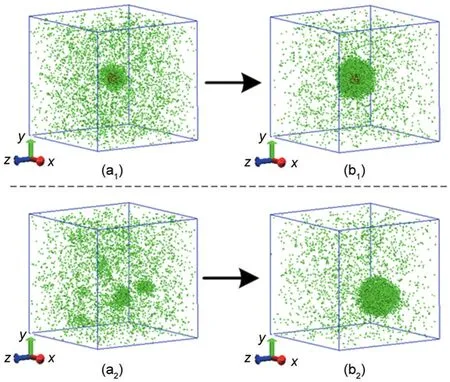
Fig.3 Snapshots of the heterogeneous and homogeneous nucleation at t=4000 ps(a)and t=8000 ps(b)for the cooling rate of 1.50×10-9J·s-1
In this section,we will examine the evolution of the system temperature during the nucleation.It is already known that vapor nucleation is an exothermic process and the latent heat of condensation is released in the form of radiation.44Therefore,how the removal heat balances with the latent heat released will significantly impact on the system temperature.
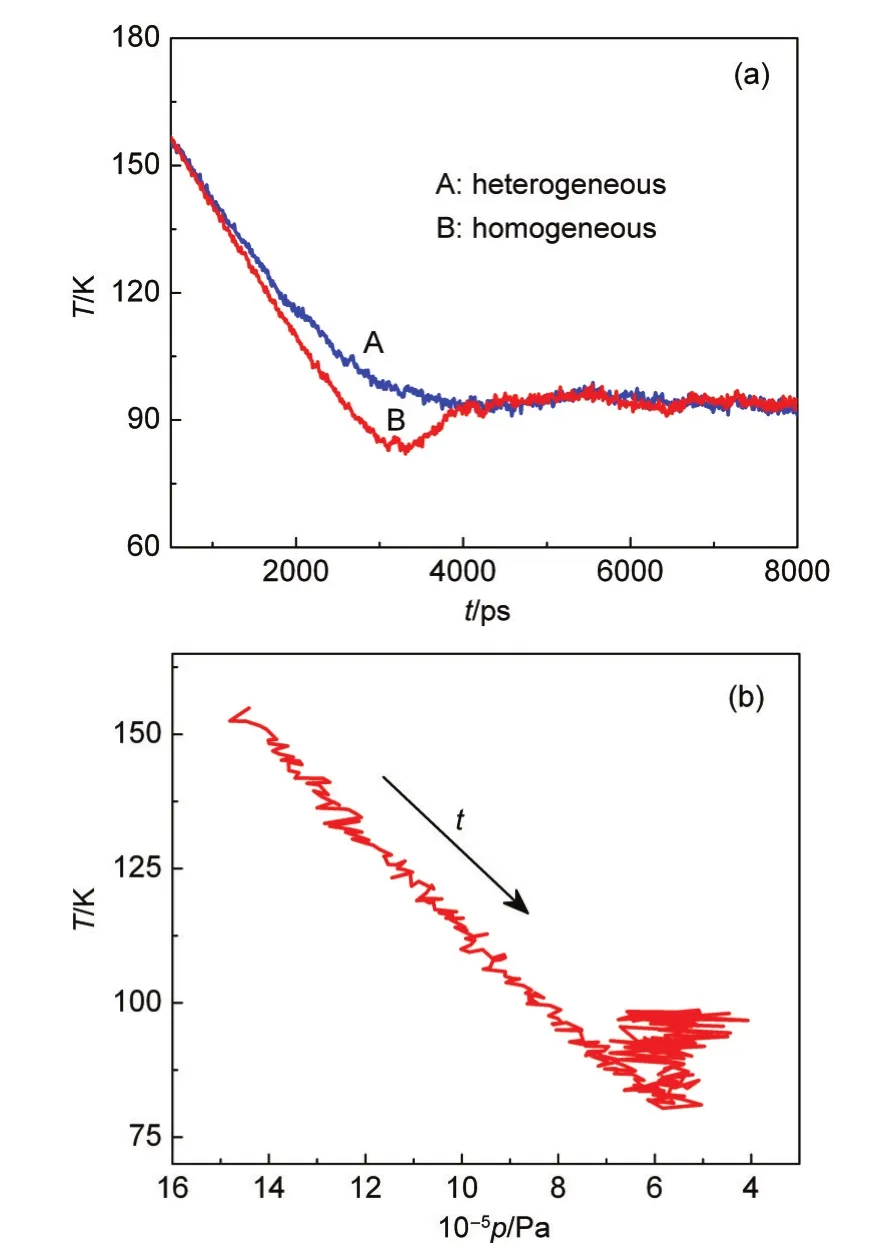
Fig.4 Comparison of the temperature variation between the homogeneous and heterogeneous nucleation(a)and relation between the temperature and pressure in homogeneous nucleation(b)
Fig.4(a)shows the temperature variation during the whole heterogeneous and homogeneous nucleation processes at the cooling rate of 1.50×10-9J·s-1.It is obviously observed that the system temperature sharply decreases,then levels off.The reduction of temperature leads the vapor to the supercooling state.Compared to the heterogeneous nucleation,at the beginning of nucleation the temperature deduce is slightly faster in homogeneous nucleation.That is because there are some atoms nucleating on the prepared solid particle and releasing a little latent heat.After 4000 ps,the system reaches at one steady state,where the rate at which the condensation vapor releases the latent heat almost equals to the heat removal rate and the temperature is the nucleation one.Moreover,the“V”shape emerges in the temperature profile of homogeneous nucleation.At the lower point of the profile,the formation of homogeneous clusters almost stops and then the agglomeration and coalescence among clusters happens,which will release more latent heat and result in the rise of the temperature.Meanwhile,the change of the temperature with the pressure in homogeneous nucleation is given in Fig.4(b).Clearly,during the nucleation,the temperature decreases linearly with the pressure.At the end of the nucleation,this linear relation between the temperature and the pressure is not satisfied.

Fig.5 Change of the temperature with time during the process of heterogeneous nucleation for the different cooling rates(a)and at the cooling rate of 3.75×10-10J·s-1(b)
When the cooling rate changes,the system temperature will change in different behaviours(seen in Fig.5(a))during the heterogeneous nucleation process.When the cooling rate is relatively small,it takes more time to perform the nucleation and arrive at a stable temperature.In the case ofq=3.75×10-10J·s-1,about 12000 ps is required to achieved the nucleation temperature as shown in Fig.5(b).If the cooling rate enhances,the higher nucleation temperature yields.When the cooling rate is equal to 0.75×10-9and 1.50×10-9J·s-1,the temperature is about 101.83 and 95.84 K,respectively.Furthermore,when the higher cooling rate is imposed,the“V”shape in the temperature profile can also emerge in the heterogeneous nucleation.It indicates that homogeneous nucleation as well occurs in the heterogeneous nucleation process at the cooling rate of more than 2.25×10-9J·s-1.Moreover,the higher cooling rate(≥2.25×10-9J·s-1),the more dramatic progresses of homogeneous nucleation.Additionally,in the cases of E and F in Fig.5(a),the continuous decrease of temperature is observed,this is because the density of vapor becomes much smaller in the following nucleation process and the latent heat released is not enough to balance the continuous removal heat.
3.3 Cluster number distribution
From Fig.3,it is already known that many small clusters are formed and broken repeatedly,only several clusters larger than the critical size will survive,and then those clusters grow up during the homogeneous nucleation.To estimate the critical cluster size,Fig.6 gives the relation between the numbers of cluster larger than a threshold size(nt)and nucleation time in the system with the pre-existing nucleus at the cooling rate of 3.75×10-9J·s-1.It can be observed that the increase of the number of clusters has similar inclination fornt=20-50 while the increase fornt=10 is faster.It suggests that many clusters smaller than 10 are formed in this stage,but only clusters larger than 20 are able to grow.So the critical cluster size is about 20.

Fig.6 Relation between the numbers of clusters larger than a threshold size(nt)and nucleation time in heterogeneous nucleation at the cooling rate of 3.75×10-9J·s-1including the cluster formed on the pre-existing nucleus
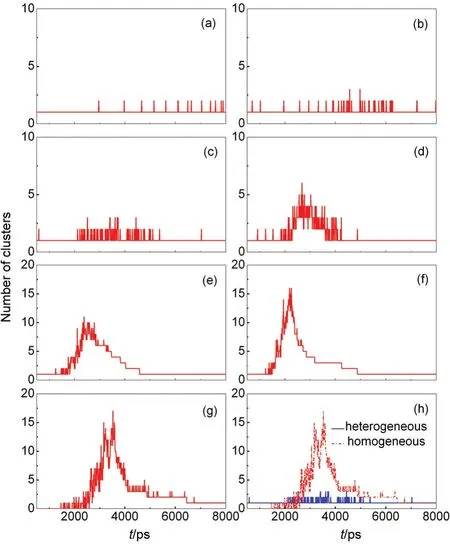
Fig.7 Change of the number of clusters(cluster size is larger than 20)with time during the heterogeneous nucleation for the different cooling rates(in J·s-1)of 3.75×10-10(a),0.75×10-9(b),1.50×10-9(c),2.25×10-9(d),3.00×10-9(e),3.75×10-9(f),and the homogeneous nucleation(g)as well comparison between two nucleation processes at the cooling rate of 1.50×10-9J·s-1(h)including the cluster formed on the pre-existing nucleus
During the nucleation process,vapor atoms do not only nucleate onto the pre-existing nucleus,other homogenous nuclei can be generated in the system.The time dependence of the numbers in clusters for the different cooling rates is given in Fig.7(a-f).When the cooling rate is relatively low,such as 3.75×10-10,0.75×10-9,and 1.50×10-9J·s-1,one cluster with the solid nanoparticle as the nucleus stably exists in the system.In fact,one or two clusters with the homogeneous nucleus can be formed occasionally,but due to molecule collision,these homogenous clusters are broken or absorbed by the heterogeneous cluster.With the cooling rate increasing,except for the heterogeneous cluster more homogeneous clusters can generate,and even 15 clusters form at the cooling rate of 3.75×10-9J·s-1.This indicates that the cooling rate plays an important role in the dynamic behaviour of the heterogeneous nucleation.Additionally,from Fig.7,we can clearly see that the nucleation process can be divided into two stages:one is the cluster formation,and the other is the cluster growth.Finally,all clusters form a liquid droplet.For comparison purpose,the homogeneous nucleation process and the corresponding comparison are shown in Fig.7(g,h)at the cooling rate of 1.50×10-9J·s-1.At the same cooling rate,there are more clusters forming in the system without pre-existing nuclei at the stage of the cluster formation.However for the heterogeneous nucleation,the clusters aggregate on the surface of the solid nanoparticle,only a few clusters form in other positions of the system.
In addition,from Fig.7 it can be clearly seen that one critical cooling rate exists at which the homogeneous clusters generated and the critical cooling rate value is between 1.50×10-9and 2.25×10-9J·s-1.Together with another two cases,in which the time dependence of the number of cluster is shown in Fig.8 at the cooling rates of 1.80×10-9and 1.875×10-9J·s-1,the critical cooling rate can be estimated to be 1.80×10-9J·s-1.
3.4 Number of atoms in cluster
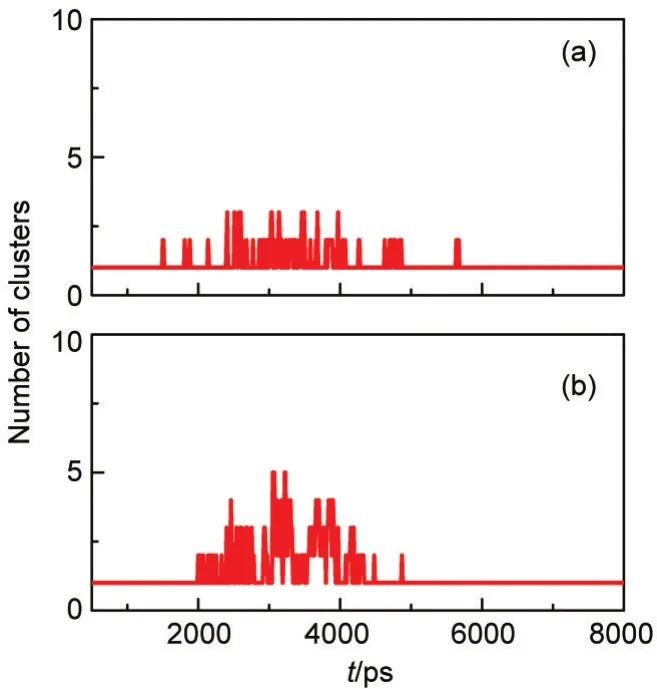
Fig.8 Variation of the number of clusters(cluster size is larger than 20)with time in the heterogeneous nucleation at the cooling rates of 1.80×10-9J·s-1(a)and 1.875×10-9J·s-1(b)

Fig.9 Change of the number of atoms in the largest cluster with time during two nucleation processes at the cooling rate of 1.50×10-9J·s-1(a)and the heterogeneous nucleation at different cooling rates(b)
In order to further understand two nucleation processes,we counte the numbers of atoms in the largest cluster,and the results are shown in Fig.9.At the beginning of nucleation,the largest cluster in the heterogeneous nucleation grows faster than the one in the homogeneous nucleation,because the presence of the solid particle acting as the nucleus results in more vapor atoms nucleating onto the surface of the particle.At 4250 ps,an obvious combination among clusters is observed in homogeneous nucleation process.After then,the numbers of atoms in largest clusters are almost same in two systems.Furthermore,Fig.9(b)gives the evolution of the largest cluster during the heterogeneous nucleation for the different cooling rates.The growth speed of the largest cluster increases with the increase of the cooling rate.When the cooling rate equals to 3.75×10-9J·s-1,a clear jump appears,because some homogeneous clusters generated aggregate with the heterogeneous cluster.Actually,there also exists the jump at the cooling rate of 2.25×10-9and 3.00×10-9J·s-1,but it is not too obvious to be seen.
We further examined the time dependence of the total number of atoms in all the clusters and the result is plotted in Fig.10.By contrast to Fig.9(b),it can be found that the total number of atoms in all the clusters are almost same as one in the largest cluster at the cooling rates of 3.75×10-10,0.75×10-9,and 1.50×10-9J·s-1.This indicates that when the cooling rate is relatively lower,heterogeneous nucleation dominates during the whole process of nucleation and homogeneous nucleation seldom emerges.When the higher cooling rate is imposed,homogeneous nucleation can happen and coexist with heterogeneous nucleation,but heterogeneous nucleation still dominates in the nucleation process.It can be seen from Fig.11,before 4250 ps much more vapor atoms nucleate onto the heterogeneous nucleus than onto the homogeneous nuclei,and then all the homogeneous clusters are attached to the centre heterogeneous cluster,finally forms a larger liquid droplet.
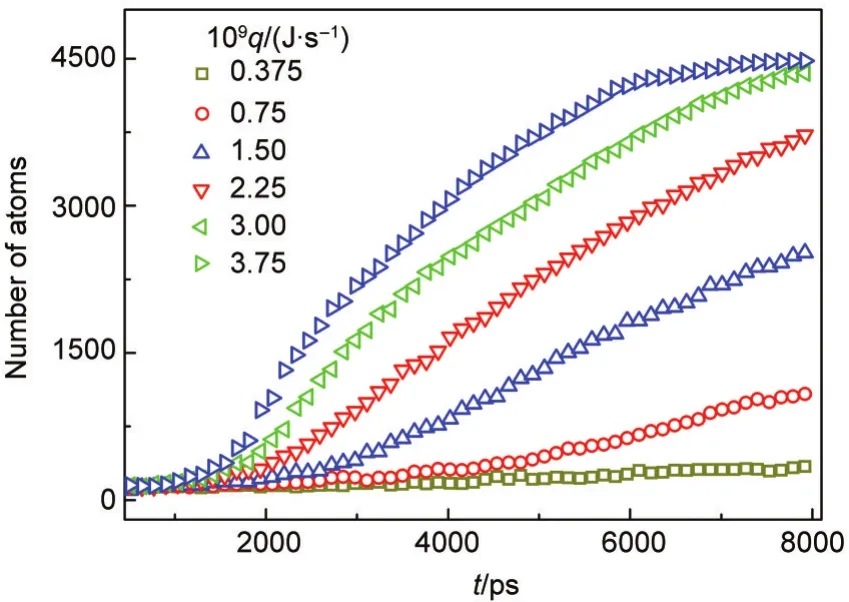
Fig.10 Change of the number of the total atoms in clusters with time at different cooling rates
Additionally,nucleation velocity(νn)is introduced to characterize the nucleation process and defined as the number of atoms nucleating and forming the clusters per unit time per unit volume.


Fig.11 Change of the number of atoms in clusters with time at the cooling rate of 3.75×10-9J·s-1in the system with the pre-existing nucleus
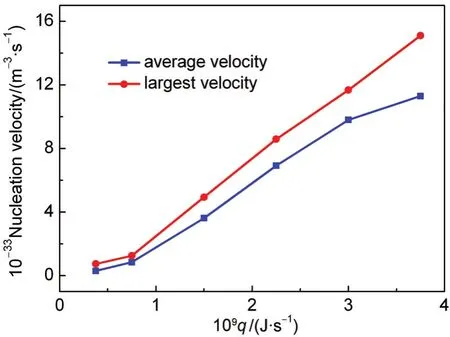
Fig.12 Change of the averaged and largest nucleation velocity with cooling rate
According to the evolution of the total atoms in clusters,we can determine the largest and average nucleation velocity for the different cooling rates(shown in Fig.12).In which,the larg-est nucleation velocity is calculated during the period from 1000 to 2000 ps,because the density of argon vapor is bigger and nucleation actives during this period.And the average nucleation velocity is obtained from 1000 to 6000 ps.From the figure,it is seen that as the cooling rate increases the largest nucleation velocity increases sharply and the average one changes linearly.
4 Conclusions
In this paper,the mechanism of heterogeneous nucleation of argon vapor on a spherical solid particle was studied by using molecular dynamics simulation.For the different cooling rates,the different nucleation temperature can be achieved for the heterogeneous nucleation.When the LJ vapor is in the superheated state of 155.8 K,this nucleation temperature is 101.83 and 95.84 K at the cooling rates of 0.75×10-9and 1.50×10-9J·s-1,respectively.According to the cluster distribution,we can find that the heterogeneous nucleation dominates at the cooling rate of lower than 2.25×10-9J·s-1,the homogeneous nucleation appeares at the critical cooling rate of 1.80×10-9J·s-1and becomes stronger as the cooling rate increases.Additionally,with the increase of the cooling rate,the largest nucleation velocity increases sharply,but the average nucleation velocity changes linearly.
In the heterogeneous nucleation,the supercooling vapor atoms are prone to nucleate onto the pre-existing nucleus to form a cluster and keep growing,not rather than form the homogenous nucleus.But on the certain condition,homogeneous nucleation emerges during the heterogeneous nucleation,so the formation,disappearance and growth of these homogenous nuclei are of importance for the system with the already existent nucleus,and the corresponding mechanism will be further investigated.
(1) Liu,X.;Meng,C.G.;Liu,C.H.Phase Transit.2006,79,249.doi:10.1080/01411590600689021
(2) Mei,Q.S.;Lu,K.Prog.Mater.Sci.2007,52(8),1175.doi:10.1016/j.pmatsci.2007.01.001
(3) Jian,Z.Y.;Li,N.;Zhu,M.;Chen,J.;Chang,F.G.;Jie,W.Q.Acta Mater.2012,60(8),3590.doi:10.1016/j.actamat.2012.02.038
(4) Sandoval,L.;Urbassek,H.M.Nano Lett.2009,9(6),2290.doi:10.1021/nl9004767
(5) Luce,F.P.;Kremer,F.;Rebon,S.;Fabrim,Z.E.;Sanchez,D.F.;Zawislak,F.C.;Fichtner,P.F.P.J.Appl.Phys.2011,109(1),014320.doi:10.1063/1.3530844
(6) Zhang,A.L.;Liu,R.S.;Liang,J.;Zheng,C.X.Acta Phys.-Chim.Sin.2005,21(4),347.[张爱龙,刘让苏,梁 佳,郑采星.物理化学学报,2005,21(4),347.]doi:10.3866/PKU.WHXB20050402
(7) Gao,T.H.;Liu,R.S.;Zhou,L.L.;Tian,Z.A.;Xie,Q.ActaPhys.-Chim.Sin.2009,25(10),2093.[高廷红,刘让苏,周丽丽,田泽安,谢 泉.物理化学学报,2009,25(10),2093.]doi:10.3866/PKU.WHXB20090928
(8) Liu,X.;Meng,C.G.;Liu,C.H.Acta Phys.-Chim.Sin.2004,20(3),280.[刘 新,孟长功,刘长厚.物理化学学报,2004,20(3),280.]doi:10.3866/PKU.WHXB20040313
(9) Steer,B.;Gorbunov,B.;Rowles,J.;Green,D.J.Chem.Phys.2012,136,054704.doi:10.1063/1.3681400
(10) Tien,L.C.;Chen,Y.J.Appl.Surf.Sci.2012,258,3584.doi:10.1016/j.apsusc.2011.11.120
(11) Wind,R.W.;Fabreguette,F.H.;Sechrist,Z.A.;George,S.M.J.Appl.Phys.2009,105,074309.doi:10.1063/1.3103254
(12) Jung,D.S.;Venart,J.E.S.;Sousa,A.C.M.Int.J.Heat Mass Transf.1987,30(12),2627.doi:10.1016/0017-9310(87)90144-X
(13) Minemawari,H.;Yamada,T.;Matsui,H.;Tsutsumi,J.;Haas,S.;Chiba,R.;Kumai,R.;Hasegawa,T.Nature2011,475,364.doi:10.1038/nature10313
(14)Maynard,A.D.;Baron,P.A.;Foley,M.;Shvedova,A.A.;Kisin,E.R.;Castranova,V.J.Toxicol.Environ.Health2004,67,87.doi:10.1080/15287390490253688
(15) Kulmala,M.;Pirjola,L.;Makela,J.M.Nature2000,404,66.doi:10.1038/35003550
(16)Kulmala,M.;Kerminen,V.M.Atmos.Res.2008,90,132.doi:10.1016/j.atmosres.2008.01.005
(17) Fletcher,N.H.J.Chem.Phys.1958,29,572.doi:10.1063/1.1744540
(18) Kimura,T.;Maruyama,S.Microsacle Thermophys.Eng.2002,6,3.doi:10.1080/108939502753428202
(19)Maruyama,S;Kimura,T.A.Molecular Dynamics Simulation of a Bubble Nucleation on Solid Surface.Proceedings of the 5th ASME/JSME Joint Thermal Engineering Conference,March 15-19,San Diego,California.1999,AJTE99-6511.
(20) Rz˙ysko,W.;Patrykiejew,A.;Sokotowski,S.Phys.Rev.E2008,77,061602.
(21) Kashchiev,D.Nucleation:Basic Theory with Applications;Butterworth Heinemann:Oxford,2000.
(22)Hegg,D.A.;Baker,M.B.Rep.Prog.Phys.2009,72,056801.doi:10.1088/0034-4885/72/5/056801
(23) Lazaridis,M.;Hov,Ø.;Eleftheriadis,K.Atmos.Res.2000,55,103.doi:10.1016/S0169-8095(00)00059-4
(24) Winkler,P.M.;Steiner,G.;Vrtala,A.;Vehkamäki,H.;Noppel,M.;Lehtinen,K.E.J.;Reischl,G.P.;Wagner,P.E.;Kulmala,M.Science2008,319,1374.doi:10.1126/science.1149034
(25) Frenkel,J.Kinetic Theory of Liquids;Clarendon Press:Oxford,1946.
(26) Chaikin,P.M.;Lubensky,T.C.Principles of Condensed Matter Physics;Cambridge University Press:Cambridge,1995.
(27) Inci,L.;Bowels,R.K.J.Chem.Phys.2011,134,114505.doi:10.1063/1.3565479
(28) Song,F.H.;Liu,C.;Xie,H.J.Eng.Thermophys.2011,32,1099.[宋粉红,刘 朝,解 辉.工程热物理学报,2011,32,1099.]
(29) Xie,H.;Liu,C.;Liu,B.W.Acta Phys.-Chim.Sin.2009,25(5),994.[解 辉,刘 朝,刘彬武.物理化学学报,2009,25(5),994.]doi:10.3866/PKU.WHXB20090404
(30) Cao,B.Y.;Chen,M.;Guo,Z.Y.Phys.Rev.E2006,74,066311.doi:10.1103/PhysRevE.74.066311
(31) Maroo,S.C.;Chung,J.N.J.Colloid Interface Sci.2008,328,134.doi:10.1016/j.jcis.2008.09.018
(32) Yi,P.;Poulikakos,D.;Walther,J.;Yadigaroglu,G.Int.J.Heat Mass Tranf.2002,45,2087.doi:10.1016/S0017-9310(01)00310-6
(33)Zhou,J.;Zhu,Y.;Wang,W.C.;Lu,X.H.;Wang,Y.R.;Shi,J.Acta Phys.-Chim.Sin.2002,18(3),207.[周 健,朱 宇,汪文川,陆小华,王延儒,时 钧.物理化学学报,2002,18(3),207.]doi:10.3866/PKU.WHXB20020304
(34) Luo,F.;Gao,J.;Cheng,Y.H.;Cui,W.;Ji,M.J.Acta Phys.-Chim.Sin.2012,28(9),2191.[罗 芳,高 剑,成元华,崔 巍,计明娟.物理化学学报,2012,28(9),2191.]doi:10.3866/PKU.WHXB201207063
(35)Liao,R.J.;Zhu,M.Y.;Zhou,X.;Yang,L.J.;Yan,J.M.;Sun,C.X.Acta Phys.-Chim.Sin.2011,27(4),815.[廖瑞金,朱孟兆,周 欣,杨丽君,严家明,孙才新.物理化学学报,2011,27(4),815.]doi:10.3866/PKU.WHXB20110341
(36) Lennard-Jones,J.E.Proc.R.Soc.Lond.A1924,106(738),441.
(37) Lennard-Jones,J.E.Proc.R.Soc.Lond.A1924,106(738),463.
(38) Cosgrove,J.A.;Buick,J.K.;Tonge,S.J.J.Phys.A-Math.Theor.2003,36(10),2609.doi:10.1088/0305-4470/36/10/320
(39) Allen,M.P.;Tildesley,D.J.Computer Simulation of Liquids;Oxford University Press:Oxford,1989.
(40)Yasuoka,K.;Matsumoto,M.J.Chem.Phys.1998,109,8451.doi:10.1063/1.477509
(41)Swope,W.C.;Andersen,H.C.;Berens,P.H.;Wilson,K.R.J.Chem.Phys.1982,76(1),637.doi:10.1063/1.442716
(42) Hunenberger,P.H.Adv.Polymer.Sci.2005,173,105.doi:10.1007/b98052
(43) Napari,I.;Julin,J.;Vehkamäki,H.J.Chem.Phys.2009,131,244511.doi:10.1063/1.3279127
(44) Buyevich,Y.A.;Natalukha,I.A.Int.J.Heat Mass Transf.1996,39,2363.doi:10.1016/0017-9310(95)00170-0
