Optically Active Sum Frequency Generation of Amino Acid Molecules
2013-07-25YINGXiaoLIHongGangLIUHaiYangWANGHuiJILiangNian
YING Xiao LI Hong-Gang LIU Hai-Yang WANG Hui JI Liang-Nian
(1Department of Applied Physics,South China University of Technology,Guangzhou 510641,P.R.China; 2Department of Chemistry,South China University of Technology,Guangzhou 510641,P.R.China; 3State Key Laboratory of Optoelectronics Materials and Technologies,Sun-Yat Sen University,Guangzhou 510275,P.R.China)
1 lntroduction

Fig.1 Structures of four amino acids:alanine(Ala),valine(Val),isoleucine(Ile),and glycine(Gly)
Using sum frequency generation(SFG)to detect the chirality of optically active(OA)solutions was firstly proposed by Giordmaine1in 1965.Since then,significantprogress of OA-SFG has been obtained.2-8Lots of small chiral molecules,such as arabinose,9,10amino acids,11bi-naphthol12and helicenes,13have been investigated by SFG.OA-SFG spectroscopy has become a useful method to detect the protein secondary structures at interfaces.14-17Although SFG becomes a powerful tool to probe the molecular chirality now,reliable calculation of OA-SFG still remains a challenging task.Ab initiocalculation had been used to investigate the sum-frequency of optically active R-monofluoro-oxirane and R-(+)-propylene oxide,it truned out that the second-order susceptibility is about two orders of magnitude smaller than the experimentally recorded values.18The general theory for OA-SFG from molecules made of a chiral center and an achiral chrompphore in isotropic solution was developed by Ji and Shen,19which is called dynamic coupling model(DCM).DCM calcalations were performed at semiquantitative level based on only four excited sates.Ab initiocalculation of the rotatory strength tensor of optical active molecules demonstrated the gauge origin invariance of the tensor obtained in the velocity formulation regardless of basis set quality,as contrasted to the non-invariance of the finite basis set results obtained in the length formulation.20The calculation of OA-SFG may have the same regulation.Here,we wish to report the OA-SFG simulation in dipole length and dipole velocity formalism by using sum-over-states(SOS)theory.Four amino acids L-alanine(Ala),L-valine(Val),L-isoleucine(Ile),and glycine(Gly)were used as model compounds(Fig.1).The results show dipole velocity formalism method provides more precise simulated OA-SFG spectra.
2 Theories

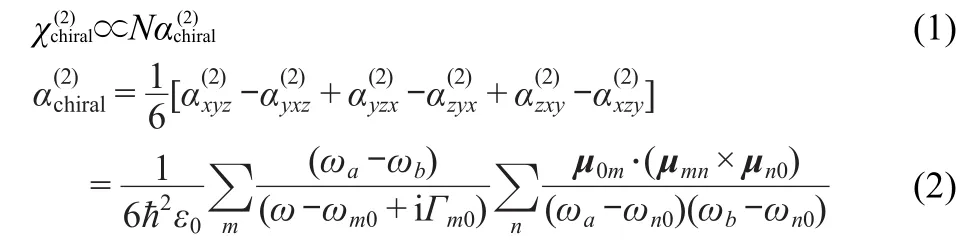
in which,Гm0=C0ωm0,ω=ωa+ωb.Nis the number density of the molecular.ħis the reduced Planck constant.ε0is the dielectric constant.ωaandωbdenote input frequency,whileωstands for the sum frequency.x,y,andzare defined as the molecular coordinate system.Гm0andωm0denote damping constant and transition frequency between excited and ground states,ωn0is the transition frequency between ground state and excited state,andC0is an empirical constant(0.016)18.An important conclusion from Eq.(2)is that in order for OA-SFG to be allowed,the three dipole transition moments,μ0m,μmn,andμn0must not be coplanar,the microscopic description of the three transition moments nonplanarD(m,n)is given by:21

Eq.(3)denotes the trip product of transition dipole moments(TP-TDM),which determines the final SFG spectra.Calculations were performed in the dipole length and velocity representations.To compare values directly,the velocity components should be transferred by Eq.(4)and Eq.(5).22Two kinds of mechanisms can be derived e-e and v-v,and two kinds of trip products also arise.One isDe-e(m,n),which is calculated from transition electric dipole moment(TEDM)and represented by TP-TEDM,the other isDv-v(m,n),which transferred through Eq.(4)and Eq.(5)22,based on dipole velocity,represented by TP-TVDM(TVDM means transferred velocity dipole moments based on dipole velocity).
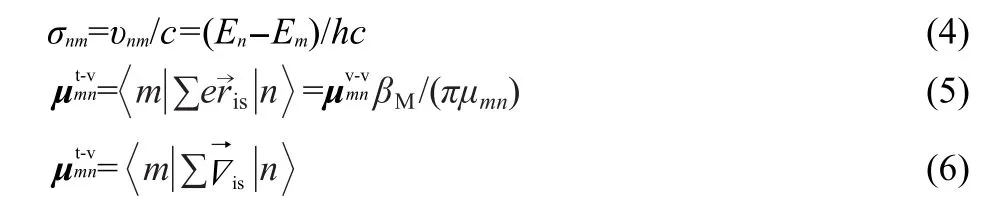
In Eq.(4)and Eqs.(5,6),μt-v,μv-v,δnm,υnm,En,c,Δis,andβMare the transferred velocity dipole moments,dipole velocity,the wavenumber,the frequency,the energy,the light speed,the“del operator”,and the Bohr magneton,respectively.eis charge of the electron.
All the calculations were performed by the Gaussian 03 program package.23The equilibrium structure of L-amino acids Ala,Val and Ile and the achiral Gly have been fully optimized byab initioRHF method at the 6-311++G**level.The excited energies and transition dipole moments were calculated by the configuration interaction singles(CIS)method using 6-311++G**basis set.24We have used self-consistent reaction field(SCRF)approach with polarizable continuum model(PCM)25for geometry optimization and the hyperpolarizability calculation.Water was used as solvent during the optimizing and computing process,there is no imaginary frequency appearing in the optimized log file and the calculated result showed that the stationary point was found,so the lowest energy conformation of the four amino acids have been obtained.
3 Results and discussion
3.1 Geometry structure optimization and electrical property
The optimized lowest energy geometries and atomic numbering of investigated amino acids and formic acid anion(HCOO-)are shown in Fig.2.The conformations of amino acids refer to literature;26selected geometrical parameters are summarized in Table 1.
Formic acid anion has aC2vsymmetric structure.The bond angle of O2=C1=O3is 127.7°.The O2=C1and C1=O3bond lengths of formic acid anion are equal(0.1235 nm).The parameters of amino acids are sensitive to the size of neighboring group,the bond angles of O2=C1=O3of four amino acids follow an order of Gly(125.8°)>Ala(125.4°)>Val(125.3°)=Ile(125.3°),which is in accordance with the increasing steric interaction between R and―COO-group from Ala(R=CH3)to Ile(R=CH(CH3)CH2CH3).

Fig.2 The lowest energy geometries of four amino acids and formic acid anion(HCOO-)

Table 1 Selected geometry parameters of four amino acids and HCOO-
The calculated magnitude and directions of electric dipole transition moments involving states|g〉↔e2〉,|e1〉↔e3〉for the four-state model are summarized in Table 2.It can be seen from Table 2 that transitions|g〉↔|e2〉and|e1〉↔|e3〉ofC2vcarboxylate anion group HCOO-are not allowed along they-direction.Their TEDM and TVDM values alongy-direction are zero.For chiral amino acids,the interaction between side group and HCOO-chromophore lowers its symmetry.This makesμ|g〉↔|e2〉andμ|e1〉↔|e3〉nonvanishing in perturbative interaction19.
In order to have a better understanding of how chirality is induced in the achiral chromophore and the induced chirality is responsible for the SFG response of different amino acids,the microscopic descriptions of the three nonplanar transition momentsD(m,n)were obtained by perturbation calculation.For convenience,four amino acids are categorized into two groups.One is Gly and Ala,the other is Val and Ile.Fig.3 shows the comparison ofD(m,n)for achiral amino acid Gly(green)and for chiral amino acids Ala(black)in the 2nd excited state(n=2)versusto themth excited state.Note that the black and green lines are quite different.TP-TDM of Gly is almost zero for every excited state in both of the dipole length and dipole velocity formalisms.As for Ala,many of its excited states exhibit nonvanishing terms ofD(m,n).This could be explained by the difference of configuration between chiral and achiral amino acids.For achiral amino acids Gly,dihedrals of O2C1C4N and O2C1C4O3are 178.6°and-179.8°(Table 1).This means that O2C1C4N and O2C1C4O3lie almost in the same plane.Electric dipole transition momentsμ0m,μmn,andμn0must be coplanar.Thus,achiral amino acid Gly has the expected zero value ofD(m,n).In contrast,the dihedral O2C1C4N of chiral amino acids Ala becomes 174.2°.The introduction of methyl makes O2C1C4N and O2C1C4O3noncoplanar.So terms ofD(m,n)is not all vanished.The differences between TP-TDM of chiral and achiral amino acids will determine final OA-SFG.Calculation results show that chiral amino acids exhibit SFG spectra;whereas,achiral Gly has no SFG signal.The agreement between the experimental and the calculation is satisfactory.It can be seen that contribution from only a few excited electronic states near the lowest excited states plays the dominant role.Of all Ala excited states,Dv-v(m,n)of the lowest excited state(m=1)is the biggest,while contributions from higher energy excited states withm>15 are neglectable.
It can be seen from Fig.4 that the TP-TDM of Val and Ile are almost the same at the low enegy excited electronic states|e1〉,|e2〉and|e3〉both in the dipole length and velocity formalisms.Because the two molecules have similar configuration and bond lengths(Table 1).However,there are obvious differences between the Val and Ile molecules above 4th excited state.e.g.,as shown in Fig.4(b),termDv-v(4,2)=0.028 for Ile and 0 for Val,and valueDv-v(5,2)of Val is only half of the Ile's.The configuration of both molecules is quite similar.The only difference is that Ile has more methyl groups than Val.The extra methyl group on Ile may induce largerD(m,n)values.The difference between their structures has significant influence on theD(m,n)term and SFG spectra.The perturbation-induced differences in termD(m,n)are responsible for the different intensity of SFG spectra.This will be further discussed in Section 3.2.It is noteworthy that the values ofD(m,n)near the lowest excited electronic state(m=1,2,3,4,5)are much larger than those of the other excited states withm>5(Fig.4),which may also justify the rationality of the assumption that semi-quantitative estimation of SFG spectra can be calculated by four-states model.

Table 2 Transition electronic dipole moments and velocity dipole moments(a.u.)between the excited states g↔e2,and e1↔e3in x,y,and z-directions
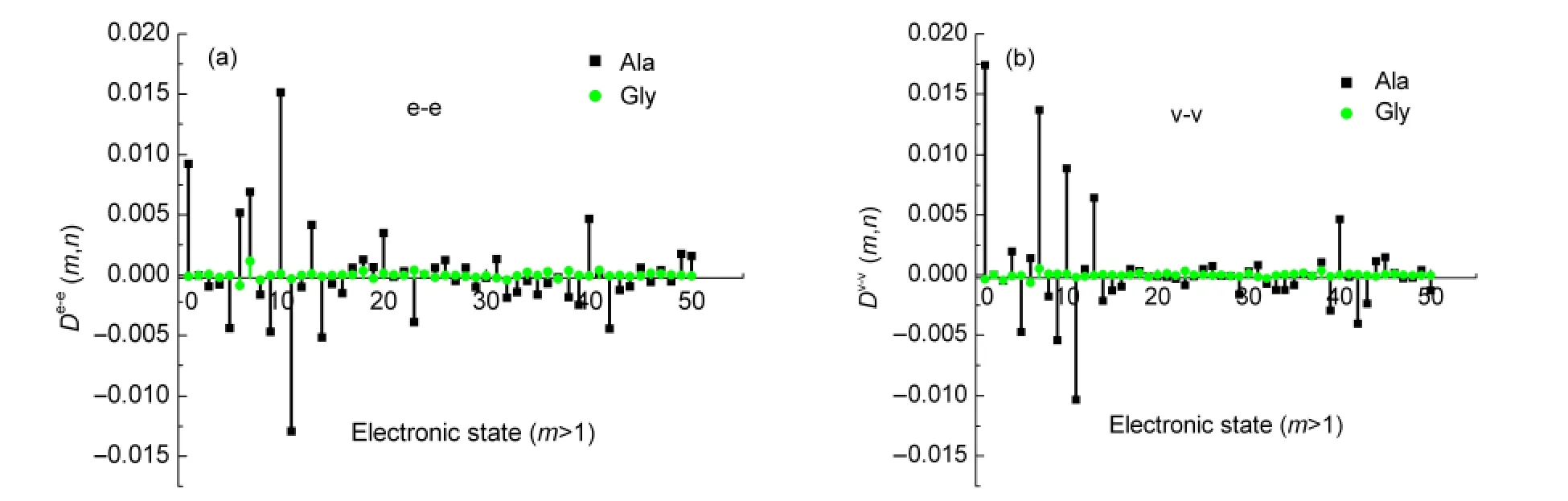
Fig.3 TP-TEDM and TP-TVDM versus the excited state(m=1-50),n fixed for 2
3.2 OA-SFG spectra


Fig.4 TP-TEDM and TP-TVDM versus the excited state(m=1-50),n fixed for 2


Table 3 Selected calculated OA-SFG spectra of four amino acids

Fig.5 Near electronically resonant OA-SFG spectra/N|2versus to SF wavelength from aqueous solution of L-Ala,L-Val,L-Ile,and Gly
4 Conclusions
The optically active sum frequency generation spectra of a series of characterized chiral amino acids in solution have been calculated in the dipole length and dipole velocity formalisms.Simulations were performed with sum over-states(SOS)theory based on theab initiorestricted Hartree-Fock(RHF)calculations and configuration interaction singles(CIS)at 6-311++G**basis set level.The magnitude and intensity order of simulated SFG spectrum is in good agreement with experimental results in the velocity representation,in contast to the failure in the dipole length method.It is showed that two calculation methods of SFG spectra are not equivalent.Dipole length formulation is origin-sensitive,and it is not suitable for the OA-SFG calculation.The velocity formalism is preferable in OA-SFG spectra simulation.
(1) Giordmaine,J.A.Phys.Rev.1965,138,1599.doi:10.1103/PhysRev.138.A1599
(2) Shen,Y.R.Nature1989,337,519.
(3) Petralli-Mallow,T.;Wong,T.M.;Byer,J.D.;Yee,H.I.;Hicks,J.M.J.Phys.Chem.1993,97,1383.doi:10.1021/j100109a022
(4) Byers,J.D.;Yee,H.I.;Hicks,J.M.J.Chem.Phys.1994,101,6233.doi:10.1063/1.468378
(5) Petralli-Mallow,T.P.;Plant,A.L.;Lewis,M.L.;Hicks,J.M.Langmuir2000,16,5960.doi:10.1021/la9913250
(6)Han,S.H.;Ji,N.;Belkin,M.A.;Shen,Y.R.Phys.Rev.B2002,66,165415.doi:10.1103/PhysRevB.66.165415
(7) Fischer,P.;Buckingham,A.D.;Beckwitt,K.;Wiersma,D.S.;Wise,F.W.Phys.Rev.Lett.2003,91,173901.doi:10.1103/PhysRevLett.91.173901
(8)Oh-e,M.;Yokoyama,H.;Yorozuva,S.;Akagi,K.;Belkin,M.A.;Shen,Y.R.Phys.Rev.Lett.2004,93,267402.doi:10.1103/PhysRevLett.93.267402
(9)Rentzepis,P.M.;Giordmaine,J.A.;Wecht,K.W.Phys.Rev.Lett.1966,16,792.doi:10.1103/PhysRevLett.16.792
(10) Giordmaine,J.A.;Rentzepis,P.M.J.Chem.Phys.1967,64,215.
(11) Ji,N.;Shen,Y.R.J.Am.Chem.Soc.2004,126,15008.doi:10.1021/ja045708i
(12) Fischer,P.;Wise,F.W.;Albrecht,A.C.J.Phys.Chem.A2003,107,8232.doi:10.1021/jp027861+
(13) Beljonne,D.;Shuai,Z.;Brédas,J.L.;Kauranen,M.;Verbiest,T.;Persoons,A.J.Chem.Phys.1998,108,1301.doi:10.1063/1.475501
(14) Baugh,L.;Weidner,T.;Baio,J.E.;Nguyen,P.C.T.;Gamble,L.J.;Stayton,P.S.;Castner,D.G.Langmuir2010,26,16434.doi:10.1021/la1007389
(15) Boughton,A.P.;Nguyen,K.;Andricioaei,I.;Chen,Z.Langmuir2011,27,14343.doi:10.1021/la203192c
(16) Fu,L.;Liu,J.;Yan,E.C.Y.J.Am.Chem.Soc.2011,133,8094.doi:10.1021/ja201575e
(17) Baio,J.E.;Weidner,T.;Baugh,L.;Gamble,L.J.;Stayton,P.S.Langmuir2012,28,2107.doi:10.1021/la203907t
(18)Champagne,B.;Fischer,P.;Buckingham,A.D.Chem.Phys.Lett.2000,331,83.doi:10.1016/S0009-2614(00)01149-0
(19) Ji,N.;Shen,Y.R.J.Am.Chem.Soc.2005,127,12933.doi:10.1021/ja052715d
(20) Pedersen,T.B.;Hansen,A.E.Chem.Phys.Lett.1995,246,1.doi:10.1016/0009-2614(95)01036-9
(21) Hayashi,M.;Lin,S.H.;Shen,Y.R.J.Phys.Chem.A2004,108,8058.doi:10.1021/jp0492467
(22)Eyring,H.;Walter,J.;Kimball,G.E.Quantum Chemistry;Wiley Press:New York,1994.
(23) Frisch,M.J.;Trucks,G.W.;Schlegel,H.B.;et al.Gaussian 03,RevisionA.01;Gaussian Inc.:Pittsburgh,PA,2003.
(24) Krishnan,R.;Binkley,J.S.;Seeger,R.;Pople,J.A.J.Chem.Phys.1980,72,650.doi:10.1063/1.438955
(25) Miertus,S.;Scrocco,E.;Tomassi,J.J.Chem.Phys.1981,55,117.
(26) Ji,N.;Shen,Y.R.Chirality2006,18,146.
