改进的SDT算法

邢 锐，祁 奇，郑 滔

(南京大学软件学院，江苏南京210093)

0 引言

在工业生产过程中长期积累的数据是工业现场宝贵的资源，为诊断和处理故障提供了第一手资料，并同趋势分析、报警记录、报表打印等服务紧密结合。因此，普遍存在着存储和利用这些海量生产数据的应用需求。将数据全部存储到数据库中明显是不合适也是不现实的，因此需要进行压缩。

当前有三类实时数据库系统压缩算法:有损压缩、无损压缩和结合前两种方法的二级压缩。无损压缩不能满足存储海量数据要求。而最著名的有损压缩算法是PI的旋转门算法。本文针对旋转门算法进行了分析，改进了旋转门中由于必须存储原始数据点而限制压缩比的缺点。实验证明改进后的算法确实能够在不提高压缩误差的情况下有效提高压缩比。

1 有损压缩算法介绍

1.1 工业标准死区压缩算法［1］

很早提出的线性有损压缩算法，基本思想是:如果当前点和最后一个记录点的差值在一个阈值范围以内，就压缩当前点，否则记录当前点，向后压缩。

该算法最大的好处就是简单，实现起来没有任何难度，而缺点也很明显，压缩直线的选取过于单一，如果某一段内的点都分布在某条斜率不为0的直线周围，使用该方法得到的结果很差。另外也有人将该算法与后面介绍的算法结合起来，获得了比较好的效果［2］。

1.2 两点式压缩算法［3］

同样也是很早提出的线性有损压缩算法，其基本思想是，采用当前记录的两个点的延长线来预测后面的数据，如果使用这条延长线插值得到的数据和当前数据的值之间的偏差在一个阈值范围以内，就压缩当前点，否则记录当前点，用当前点和前一个点向后压缩。

该方法较工业标准死区压缩算法的好处就是直线的选取不再使用单一的平行于x轴的直线，而采取了两个点的连线。这样在一定程度上改善了工业标准死区算法中的缺点。但由于直线是采用了之前已经存储的两个点来确定的，因此过早确定直线导致该算法的预后性较差。没有通过后来的点来调整这条直线位置的缺陷也导致了该算法在效果上不如后面介绍的一些算法。

1.3 旋转门压缩算法［4］

美国OSI软件公司研发的用于实时数据库的有损压缩算法［4］，对于旋转门压缩算法来说，先由上一保存数据项和当前数据项来画出一条直线 (在二维坐标图上)，如果待保存数据项不在当前数据项和上一保存数据项的压缩偏差范围之内，则待保存数据项被保存。就算法的具体实现来说，有基本的旋转门压缩算法和基于斜率比较的旋转门压缩算法。旋转门压缩算法是根据数据构建一个又一个的高度 (高度即有损压缩的阈值)固定的平行四边形去“套住”数据，在不能“套住”时将前一个点进行归档 (存储)。图1为旋转门压缩算法的示意图。

图1 旋转门压缩算法示例

该方法改善了两点式压缩算法中过早确定直线的不足，采用该方法能够根据后面新来的数据调整直线的位置。这样能够很好的根据数据的发展趋势进行压缩。

但就直线的选取方法来说，仍显得有些单一。如果不限定压缩的直线必须采用首尾点的连线的话，就可以在某个压缩区域内压缩更多的点。

1.4 一些基于旋转门压缩算法的改进算法

在旋转门压缩算法基础上，有人提出了一些其它的算法，比如动态调整旋转门压缩算法中的阈值来适应数据的方法［5］，限制一次压缩的数据长度等方法［6］，识别噪声点的算法［7］，使用曲线进行拟合的算法［8］以及增量型 SDT算法［9］。

2 改进的旋转门算法

算法思想介绍

旋转门压缩算法的基本思想是，存储的数据均为原始数据。然而有损压缩算法本身就对误差有一定的容忍，经过实验发现，存储处理后的数据而非原始数据可以达到甚至超过旋转门压缩算法的压缩效果。

可以不存储原始数据而存储处理过的数据，这个是该改进算法重要思想之一。而其他的大部分的旋转门压缩改进算法都是基于原来的旋转门压缩算法做一些新的处理。比如控制阈值，限制长度等。

在压缩完一段数据以后重新选择起始点是该改进算法的另一个重要思想。由于数据变化的连续性，上一个失效的压缩点的数据失效是因为数据的发展趋势发生了变化，而此时使用上一个压缩区段的最后点来进行存储会较大的影响压缩的效果。因此在该算法中，压缩完一段数据后，重新选择下一个数据点作为下一区段的起点。

算法介绍

算法保存由当前可压缩的点组成的点集Q，每来一个新的点p和Q构成新的点集Q’。判断Q’能否用一条线段来压缩。如果可以则用Q’替换Q，继续读入新的点。如果不行则存储用于拟合点集Q中数据的线段信息，清空Q，将p添加到点集Q中，然后读入新的点，开始下一段压缩。

判断点集Q能否用线段压缩的方法:

在本题目的要求下，点集Q能够被线段压缩的条件等价于:

条件1 能够找到一条直线L，满足:Q中的所有的点到L的竖直距离不超过MAX_ERROR(MAX_ERROR为压缩算法当中的阈值)。

如果有一条直线L满足条件1，显然可以使用L来压缩和恢复数据。而如果Q可以被某条线段压缩，该线段所在的直线L显然满足条件1。

条件2 能够找到两条平行的直线L1、L2，满足:Q中所有的点都在L1的下方 (包括在L1直线上)、L2的上方 (包括在L2直线上)，同时L1、L2在竖直方向的距离d不超过2*MAX_ERROR。

显然条件1和条件2是等价的。

在满足条件2的L1、L2当中一定有某一对L1、L2，它们之间的竖直距离是最小的。假设这个距离为dMin，将对应dMin的L1和L2记为MinL1和MinL2。

条件3 Q中的MinL1、MinL2的竖直距离dMin不超过2*MAX_ERROR。

显然条件2和条件3也是等价的。

下面证明MinL1和MinL2的两个性质:

性质1 MinL1和MinL2各自至少经过Q中的一个点。

性质2 MinL1和MinL2中至少有一条经过了Q中的两个点。

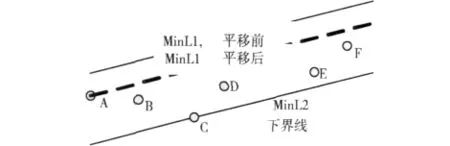
图2 性质1说明

性质1证明:用反证法来证明。

不妨设MinL1没有经过点集当中的点，如图2所示。则很明显将MinL1向下平移至经过A点的直线MinL1’后也满足条件 (2)。而此时两条平行线的距离明显小于之前的两条平行线的距离。因此之前的两条平行线不是dMin最小的两条平行线，而这与假设矛盾，因此MinL1必定经过Q中的某个点。同理可证，MinL2必定经过Q中的某个点。

证毕。

性质2证明:仍然用反证法证明。

性质1，可假设MinL1和MinL2各自都只经过了Q中的一个点，如图3所示。设MinL1经过的点为A(xA，yA)，MinL2经过的点为C(xC，yC)。假设MinL1的斜率为k，则通过计算可得，MinL1和MinL2在竖直方向的距离

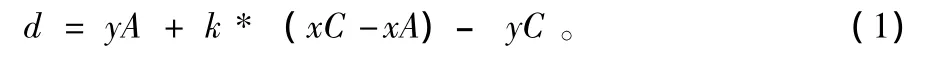
由于在某个时间点上只能有一个数据，因此Q中所有的点均不可能有相同的横坐标。

不妨设A点在C点左边，即有xA＜xC。那么由 (1)式可知，k的值越小，d也就越小。也就是说看这两条线能否绕着A点及C点顺时针旋转。

在图2中，由于两条直线都只经过点集Q中的一个点。明显可以通过将MinL1顺时针旋转至MinL1'(MinL1'经过了点集中的另一个点 F)，而将 MinL2顺时针旋转至MinL2'。其中F是两条线同时旋转时它们首先碰到的Q中的其它点。明显 MinL1'和 MinL2'是满足条件2的，而MinL1'和MinL2'的距离d小于MinL1和MinL2的距离。这与之前假设的MinL1和MinL2是最有压缩的条件矛盾，因此说明假设不成立。说明MinL1和MinL2至少有一个经过了点集Q中的两个点。

对于A点在C点右边的情况，同理可证明。

证毕。

由以上证明过程也可以看出:

性质3:MinL1和MinL2中至少有一条是点集Q中某两个点的连线L，而且 L能够将点集Q中所有的点分隔在L的一边 (包括在L上)。

由以上三条性质可知:条件3等价于条件4:

条件4:在点集Q中所有满足条件5的L中，至少有一个L满足条件6。

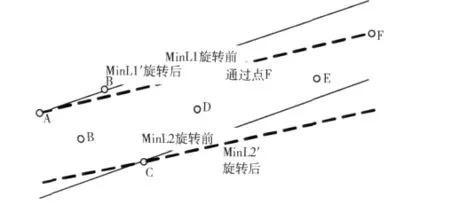
图3 性质2说明

条件5:L是Q中的某两个点的连线，而且L能够将Q中点分隔在L的一边。

条件6:Q中的点到L的最大竖直距离dmax不超过2*MAX_ERROR。

压缩算法流程

压缩算法的过程:

根据以上的分析，压缩算法设计如下:

使用一个数组LArray记录Q中所有满足条件5和条件6的L(包括直线斜率k，y轴截距b，Q中的点到L的最大竖直距离的dmax，点集Q中点和它的位置关系的一个bool变量location，点在上方为true，下方为false)，使用MinL记录LArray中dmax最小的L。

步骤1 将Q和LArray置空，读入新数据至newPoint，存储newPoint，同时将它添加到点集Q中。

步骤2 判断有没有新来点，如果没有则跳至步骤9。

步骤3 读入新数据至newPoint，并将其添加到Q中，将LArray中由于添加了newPoint而不再满足条件5和条件6的L移除。

步骤4 在newPoint和点集Q中其它点构成的直线当中，选出斜率最大的直线 kMaxL，和斜率最小的直线kMinL。显然在这些直线中，有且只有kMaxL和kMinL能够满足条件6。(如图4所示，FH和CH为kMinL和kMaxL)。

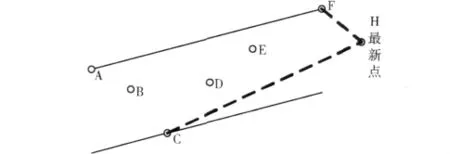
图4 新点H的加入

步骤5 判断kMaxL是否满足条件6，如果满足则将它添加到LArray当中。其中的location为true。

步骤6 判断kMinL是否满足条件6，如果满足则将它添加到LArray当中。其中的location为false。

步骤7 判断此时LArray是否为空，如果不为空，取出dmax最小的一个L保存到MinL中，并跳至步骤2。

步骤8 将MinL向location表示的方向平移dmax/2的距离，得到直线LStore。存储用来恢复数据的LStore。将Q和LArray清空，存储newPoint并将newPoint添加至Q中，跳至步骤2。

步骤9 将MinL向location表示的方向平移dmax/2的距离，得到直线LStore。存储用来恢复数据的LStore。将点集Q中最右边的点存储，算法结束。

压缩算法可行性分析:

步骤1、2、3都是简单的基本步骤，可以在O(1)时间完成。

将LArray中由于新点的加入而不再满足条件 (5)或条件 (6)的L移除。需要进行以下过程，对LArray中的每条直线判断是否满足条件 (5)和条件 (6)。需要进行点和直线位置判断、点到直线竖直距离计算基本步骤。设LArray中有K条直线，则该步可以在O(K)时间内完成。假设此时点集中点数据为N，那么容易知道点集Q中满足条件 (5)的直线不会超过N个，即K＜=N。O(N)时间内完成。

步骤4中，需要进行N-1次斜率计算和2* (N-2)次比较，同样可以在O(N)时间内完成。

步骤5和步骤6个需要N-1次距离计算和N-2距离的比较，O(N)时间完成。

步骤7需要一次判断，可能需要K-1次比较，和一次存储，O(N)时间完成。

步骤8和步骤9可以在O(1)时间内完成。

由以上分析过程可知，算法是可行的。

拟合算法流程

拟合算法的过程:

读取数据库中的两个点P1、P2，并读取存储的一个LStore信息，使用LStore来恢复P1和P2之间的数据 (不包括P1和P2)，然后读取新的点P3和一个LStore信息，使用LStore恢复P2和P3之间的数据 (不包括P2和P3)。依此类推，直到数据库中没有新的点可以读取时，算法结束。由以上描述可知，恢复算法的运行时间为O(M)，M为压缩前点的个数。

3 算法性能分析

对数据样本压缩的有关参数评估。

测试的数目为6000个数据，误差范围为分别为1和0.5。表1为误差范围为1时效果比较，表2为0.5时效果比较。

由此看来，该算法确实能够在不增加最大误差的情况下，减少压缩点的数目并减少绝对值平均误差，完成有损压缩的要求。

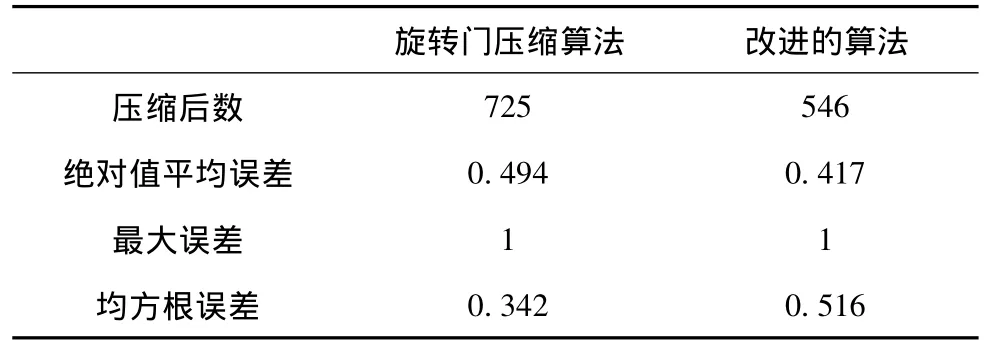
表1 误差范围为1时效果比较

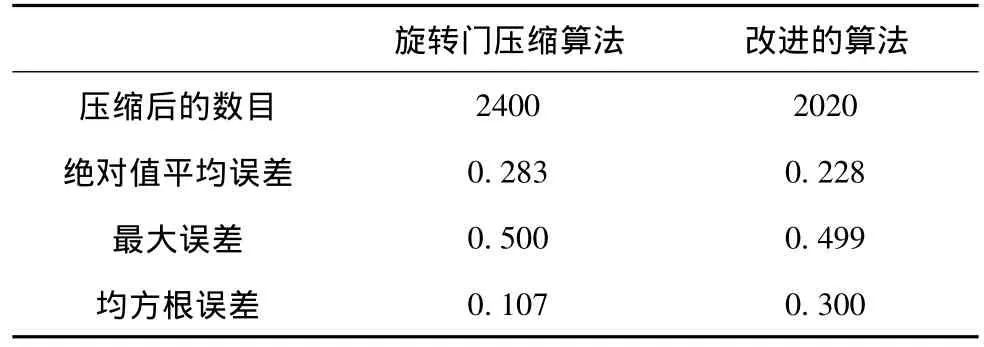
表2 误差范围为0.5时效果比较

4 结束语

本文提出了一种改进的旋转门压缩算法，并编写了程序对合成数据和实际过程数据进行了仿真计算，解决了旋转门算法中保存原始数据点和起始点选取过于单一的问题，实验数据证明该算法确实能够在不增加最大误差的情况下，减少压缩点的数目并减少绝对值平均误差，完成有损压缩的要求。改进的SDT算法计算量小，运行速度很快;并且很容易被工程技术人员所接受;它不仅可以用在过程压缩过程中，而且也可以用于过程趋势分析和识别等等。如果压缩后的数据用于压缩的话，还可以采用WinZip等软件进一步压缩的方法［10］。

［1］WANG Jun.Research and improvement of loss linear compression algorithms in the real-time database［J］.Micro Computer Application，2011，32(7):13-18(in Chinese).［王君.基于实时数据库的有损线性压缩算法研究与改进［J］.微计算机应用，2011，32(7):13-18.］

［2］ZHANGXiuxia，HAOJialong，WANGShuangxin.Analysis and implementation of rea-l time historical database of supervisory control and data acquisition configuration software［J］.North China Electric Power，2009(11):50-54(in Chinese).［张秀霞，郝佳龙，王爽心.工业监控组态软件实时历史数据库的分析与实现［J］.华北电力技术，2009(11):50-54.］

［3］Sivalingam S.Effect of data compression on controller performance monitoring［C］//Trondheim，Norway:Norwegian Univ of Sci＆Technol，2011:594-599.

［4］ZHANG Wang，CHEN XinChu，LU DingXing.Research and application of improved process data compression algorithm-SDT ［J］.Industrial Control Computer，2009(8):1-3(in Chinese).［张望陈新楚卢定兴.过程数据压缩算法SDT的改进研究与应用［J］.工业控制计算机，2009(8):1-3.］

［5］QU Yilin，WANGWenhai.Automatic parameter control sdt algorithm for process data compression ［J］.Computer Engineering，2010，36(22):40-42(in Chinese).［曲奕霖，王文海.用于过程数据压缩的自控精度SDT算法［J］.计算机工程，2010，36(22):40-42.］

［6］ZHANG Qiaofang，LI Guangyao，DING Meilin，et al.Three dimensional canning map generating algorithm from single image［J］.Computer Technology and Development，2010，20(1):22-24(in Chinese).［张巧芳，李光耀，丁关林，等.基于单幅图像的三维浏览图生成算法 ［J］.计算机技术与发展，2010，20(1):22-24.］

［7］ZHANGJian，LIU Guangbin.An new data compression based on isdt algorithm and its performance analysis［J］.Fire Control and Command Control，2007，32(2):81-82(in Chinese).［张健，刘光斌.ISDT算法的数据压缩处理及其性能分析［J］.火力与指挥控制，2007，32(2):81-82.］

［8］NING Hainan.A new process data compression algorithm based on sdt algorithm ［J］.Computer Technology and Development，2010(1):25-28(in Chinese).［宁海楠.一种基于SDT算法的新的过程数据压缩算法 ［J］.计算机技术与发展，2010(1):25-28.］

［9］ZHAO Liqiang，YU Tao，WANG Jianlin.Process data compression method based on SQL database［J］.Computer Engineering，2008，34(14):58-62(in Chinese).［赵利强，于涛，王建林.基于SQL数据库的过程数据压缩方法［J］.软件技术与数据库，2008，34(14):58-62.］

［10］ZHOU Shuangying，YU Jianqiao.Research of secondary compression algorithm of RWM ＆ DEWS data［J］.Computer Engineering，2011，37(2):40-42(in Chinese).［周双英，余建桥.RWM＆DEWS数据二次压缩算法研究［J］.计算机工程，2011，37(2):40-42.］