2013年北京中考试题第25题的几种解法及一点教学建议与反思

☉北京师范大学附属中学 毛玉忠

2012年及2013年北京市中考试题最后一道都是具有“初高中衔接功能”的创新试题.从试题上看，具有从“新定义入手”来考查学生再学习的能力，试题设计体现层层诱导，从认识到再认识到应用的学习过程，这也给北京市的初中教学工作提出了更高的思考与要求，教学中是重视“题海”还是重视“数学概念”来提升学生认知过程的教学，同时对初高中教师互通教材的“大循环”教学提出了一些思考.下面试题的解法是笔者在多年高中数学教学的基础上进行“初高中大循环”数学教学中的一些体会和想法.

一、试题的几种解法

题目1（2013年北京市中考数学试题第25题）对于平面直角坐标系xOy中的点P和⊙C，如图1，给出如下定义：若⊙C上存在两个点A，B，使得∠APB=60°，则称P为⊙C的关联点.

图1

（1）当⊙O的半径为1时.

①在点D，E，F中，⊙O的关联点是________；

②过点F作直线l交y轴正半轴于点G，使∠GFO=30°，若直线l上的点P（m，n）是⊙O的关联点，求m的取值范围.

（2）若线段EF上的所有点都是某个圆的关联点，求这个圆的半径r的取值范围.

解析：（1）①点D在⊙O内，满足；点E在圆外，向圆引切线，切线夹角恰好满足；点F也在圆外，但不满足，故答案是点D、E.

②方法1：当OP=2时，过点P向⊙O作两条切线PA，PB（A，B为切点），则∠APB=60°，所以点P为⊙O的关联点.

事实上，当0≤OP≤2时，点P是⊙O的关联点；当OP＞2时，点P不是⊙O的关联点.

如图2，以O为圆心，OG为半径作圆，设该圆与l的另一个交点为P1.

当点P在线段GP1上时，OP≤2，点P是⊙O的关联点.

当点P在线段GP1的延长线或反向延长线上时，OP＞2，点P不是⊙O的关联点.

连接OP1，可知△GOP1为等边三角形.

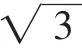
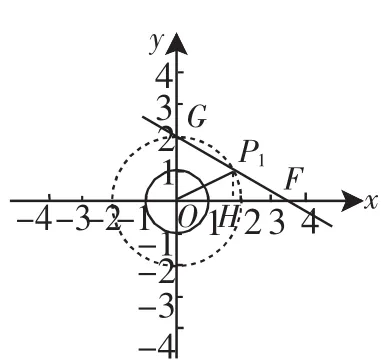
图2

图3

方法2：若点P是⊙O的关联点，过P向圆引切线PM，PN，切点分别为M，N，则有∠MPN≥∠APB=60°，连接OP，OM.

因为在Rt△PMO中，∠MPO≥30°，

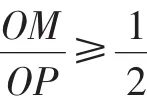
因为G（0，2），所以OG=2，所以G是关联点.

方法3：若点P是⊙O的关联点，过P向圆引切线PM，PN，切点分别为M，N，则有∠MPN≥∠APB=60°，连接OP，OM.

化简，得m（m-）≤0.

（2）方法1：设该圆圆心为C.

根据②可得，若点P是⊙C的关联点，则0≤PC≤2r.

由题意，点E，F都是⊙C的关联点，所以EC≤2r，FC≤2r，所以EC+FC≤4r.

又因为EC+FC≥EF（当点C在线段EF上时，等号成立），所以4r≥EF.

事实上，当点C是EF的中点时，对所有r≥1的⊙C，线段EF上的所有点都是⊙C的关联点，综上所述，r≥1.

方法2：根据题意，设所求⊙C的半径为r，则⊙C内及圆上的点都是关联点.

若P是圆外的点，作切线PM，PN，则∠MPN≥60°.

所以在Rt△PCM中，∠MPC≥30°.

故若点P是⊙C的关联点，则CP≤2r.

因为线段EF上所有点都是⊙C的关联点，则线段EF在以C为圆心、2r为半径的圆及内部，所以只有EF为该圆直径时，半径最小.

因为EF=4，所以4r≥4，即r≥1.

方法3：设该圆圆心为C.

根据②可得，若点P是⊙C的关联点，则PC≤2r.

由题意，点E，F都是⊙C的关联点，所以EC≤2r，FC≤2r.

所以半径取最小时点C在EF的垂直平分线上.

因为线段EF上所有点都是⊙C的关联点，所以当r最小时，点C就是垂直平分线与EF的交点，即EF的中点为C.

因为EF=4，所以2rmin=2，即rmin=1，所以r≥1.

方法4：设该圆圆心为C.

根据②可得，若点P是⊙C的关联点，则PC≤2r.

设圆心C（x，y），半径为r，则CE≤2r，CF≤2r.

二、由试题看设计思路

本题考查学生对“新定义”的理解及圆与直线、平面直角坐标系等相关知识的掌握情况.

第一步：初步了解“新定义”.

通过对特殊点D、E、F的判断，来理解“关联点”，在判断三个点是否是关联点时，发现：

（1）圆内的点一定是“关联点”；

（2）圆上的点一定是“关联点”；

（3）圆外的点到圆心在一定距离范围内的点是“关联点”.

第二步：进一步理解“新定义”.

（1）圆内及圆上的点是圆的关联点；

（2）当点P在圆外时，向圆作“切线”，切点分别为M、N时，发现“若圆上存在两点A、B，使得∠APB=60°存在，必须满足∠MPN≥60°；根据圆的切线的特点，若点P是最远的“关联点”，则OP=2，故“以O为原点，2为半径的圆及内部都是关联点”.

第三步：应用形成性的结论解决问题.

由于线段EF上的所有点都是圆的“关联点”，故点E、F也是关联点.

设圆心为C，半径为r，则CE≤2r，CF≤2r，所以CE+CF≤4r.

又因为在平面内任意三点满足CE+CF≥EF，所以4r≥EF，且点C在线段EF上时，这些圆满足“线段EF上的所有点都是某个圆的关联点”的所求圆.

三、教学建议与反思

在初中数学教学中，此类题目是创新试题，单靠“题海”学生是得不到的，在教学中要注重“数学概念”的深度教学，如在《圆与直线》的教学中，让学生完全理解直线与圆的相关概念（如位置关系的判断、距离问题，弦长问题、切线夹角问题等概念）及直线上动点与圆上点连线产生的各类相关问题深入探究一些，那么这类试题学生自然就不难解决了.比如具有高中知识特征的有：

题目2：已知点P是直线l上的动点，过点P向圆作切线PM、PN，切点分别为M、N，连接CM、CN.

（1）求四边形CMPN面积的最小值.

（2）求∠MPN的最大值.

（3）求∠MPN=α的点P横坐标的取值范围.

（4）设圆心C到直线l的距离为d.

①d与r满足什么条件时，存在∠MPN=90°、60°？

②d与r满足什么条件时，圆上存在到直线距离为2的点有1个？2个？3个？4个？

在设计问题时，取一些特殊的圆及特殊的直线，对于初中学生而言就可以解决了.