于拐角处寻“另一村”
2013-07-25湖北省武汉市第十六中学卢胜光
☉湖北省武汉市第十六中学 卢胜光
在生活中经常经过建筑的走廊的“拐角”处来回搬运一些物品,看似十分简单的事情,却隐含着颇有意义的数学背景.下面我们就把它设计成一些数学问题进行一些探讨.
问题1:某厂房内有一个水平直角型走廊,如图1所示,两过道的宽度分别为3m、2m,有一根长5m的金属棒(粗细忽略不计)能否水平通过直角走道?
分析与解答:不失一般性,设直角型走道的宽分别为a、b,如图1,以直线OA、OB分别为x轴、y轴建立直角坐标系,问题转化为:求过点P(a,b)的直线被两坐标轴所截线段AB长的最小值.

图1









所以5m长的金属棒可以水平通过直角走廊.
问题2:某建筑物内有一水平直角型走廊如图2所示,两过道的宽度均为2m,有一个水平截面为矩形的设备的宽为1m,长为5m,问该设备能否水平经过该过道?

图2
分析与解答:我们还是来讨论问题的一般性,设过道的宽度均为λ m,矩形长AB=am,宽BC=bm(这里b<λ<a),以直线OB、OA分别为x轴、y轴建立坐标系,问题转化为:求以M(λ,λ)点为圆心,半径为b的圆的切线被两坐标轴的正半轴所截线段AB长的最小值.

因为AB与圆(x-λ)2+(y-λ)2=b2相切,由圆心(λ,λ)到直线AB距离等于半径,得



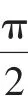


因为b<λ,当λ∈R+时,-λt2+4bt-2λ<0,


问题3:设病床的长和宽分别为p,q(规定),病房走廊宽度为l,拐角处成直角,如图3.为了保证病人能躺在病床上进入手术室,宽度l最窄应是多少?说明理由.
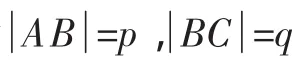

图3

再设t=sinα+cosα.












分析与解答:如图4,以∠AOB的角平分线为x轴,O为坐标原点建立平面直角坐标系.

图4






所以长为10m的竹杆可平行通过该“拐角”走廊.
上述几个问题,将实际背景融入到了高中数学内容中,反映了数学的应用价值,是开展数学建模的好素材.若能结合教学内容进行适当的整合,在实际应用中渗透,将有利于激发学生学习数学的兴趣,促进学生形成和发展数学应用意识.
