自行式高空作业平台结构稳定性分析
2013-07-25黄小征陈建平樊玉言
张 珂,黄小征,陈建平,樊玉言
(1.沈阳建筑大学 交通与机械工程学院,辽宁 沈阳 110168;2.杭州赛奇高空作业机械有限公司,浙江 杭州 310015)
高空作业平台是应用于各行业的高空作业,如高空设备安装、检修等的可移动的高空作业产品,广泛应用于电力、市政、园林、通信、机场、造船、交通、广告、摄影等高空作业领域.随着经济技术的快速发展,高空作业平台的安全与稳定问题越来越引起人们的重视,为保证结构安全及人身安全,必须要弄清整机和关键部件的正常工作载荷范围和失效机理.在稳定性研究方面,前人已经做了很多工作,得到很多有价值的研究成果.例如,刘晓婷等[1]利用力矩平衡法在研究蜘蛛式高空作业平台抗倾覆稳定性过程中,得到了单、双人负载时高空作业平台的稳定性系数范围,高空作业平台在这个稳定系数范围内可达到整体稳定;谷礼新等[2]利用有限元法在研究塔式起重机起重臂结构稳定性的过程中,得到了起重臂在典型工况下的特征值,利用该特征值就可以模拟实际情况进行稳定性分析,对塔机的设计具有指导和借鉴意义.本文应用力矩法[3]和有限元法,分别对6012型可移动式高空作业平台的整体和局部稳定性进行分析校核.
1 高空作业平台的结构组成及工况分析
1.1 结构组成
自行式高空作业平台主要由底架、支腿、升降机构、连接架、回转支撑、工作平台、护栏等组成.其中底架采用4轮驱动,并附有双转向系统和复杂地面辅助导轨移动系统;升降机构采用不平行布置的6桅柱组结构,既提高了工作平台的稳定性,又增强了升降机构在各个方向上的刚度特性;工作平台可以进行360°旋转,且在护栏两端能够加装活动式延伸装置,扩大了工作平台的工作范围.自行式高空作业平台整机三维Solidworks模型如图1所示.
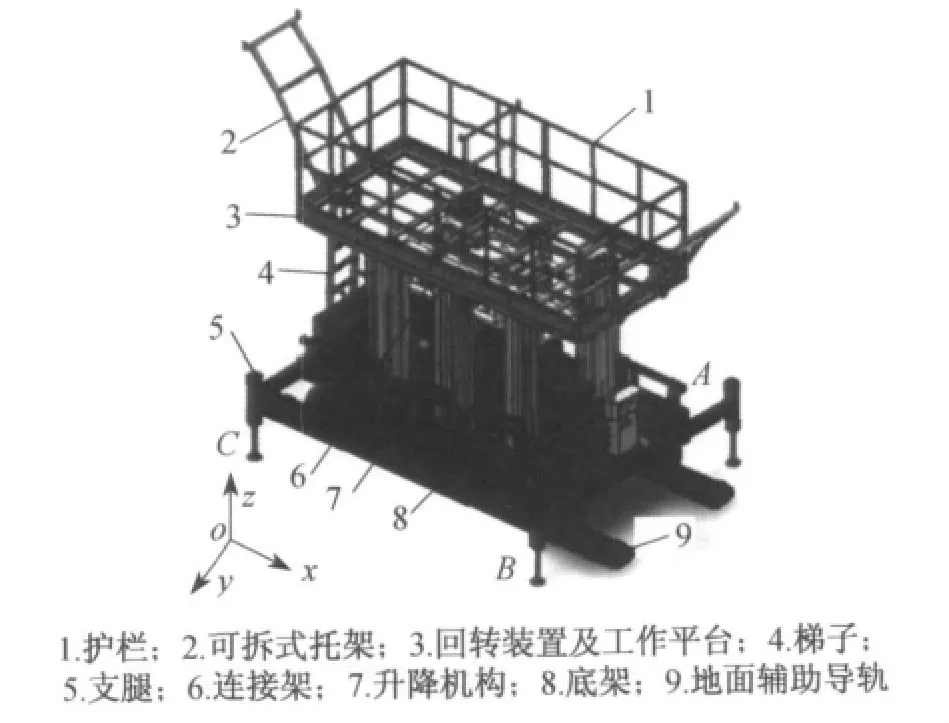
图1 自行式高空作业平台整机三维模型Fig.1 Whole three-dimensional model of self-propelled aerial work platform
1.2 工况分析
根据欧盟标准EN280,工作平台上工作人员及设备的作用位置如下所述:即2名操作员位于平台的同一边,其中操作员1位于平台左上角,操作员2位于操作员1正下方0.5m处,且离护栏边缘的距离均为0.1m;设备(物料)的集中力载荷均匀分布在平台总面积的1/4处,且位于平台的左侧;考虑x,y向风载荷,并用黑箭头表示,载荷分布如图2所示.
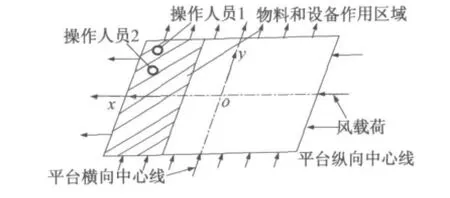
图2 工作人员及设备的作用位置Fig.2 Effect location of staff and equipment
工况1:自行式高空作业平台起升到最高位置,工作平台不旋转;工况二:自行式高空作业平台起升到最高位置,工作平台旋转90°.为了便于计算分析,假设2个工作人员都作用于第一个操作人员的位置,并用小长方体来表示,如图3,4所示.


2 整机抗倾覆稳定性分析与计算
根据高空作业平台设计规范,结合自行式高空作业平台的结构特点,借鉴已有起重机抗倾覆稳定性的计算方法,本文采用力矩平衡法分别计算出两种工况下的稳定力矩和倾覆力矩,并进行验算[4].
2.1 工况1下的抗倾覆稳定性模型求解
为了便于观察并节省空间,下面用平台缩合状态来表示平台起升到最高位置状态.自行式高空作业平台横向和纵向的受力分析如图5,6所示.
在工况1条件下,利用力矩平衡法,分别列出高空作业平台横向和纵向整机抗倾覆稳定性的数学模型.
2.1.1 工况1下的平台横向整机抗倾覆稳定性分析稳定力矩为
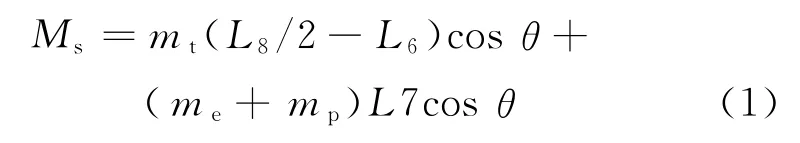
式中:Ms为稳定力矩;mt为机器总质量;L8为2个支腿之间中心距离;L6为整机偏心距离;θ为底架允许的最大倾角;me为设备质量;mp为工作人员总质量;L7为工作人员重心与左侧支腿支点之间的距离.
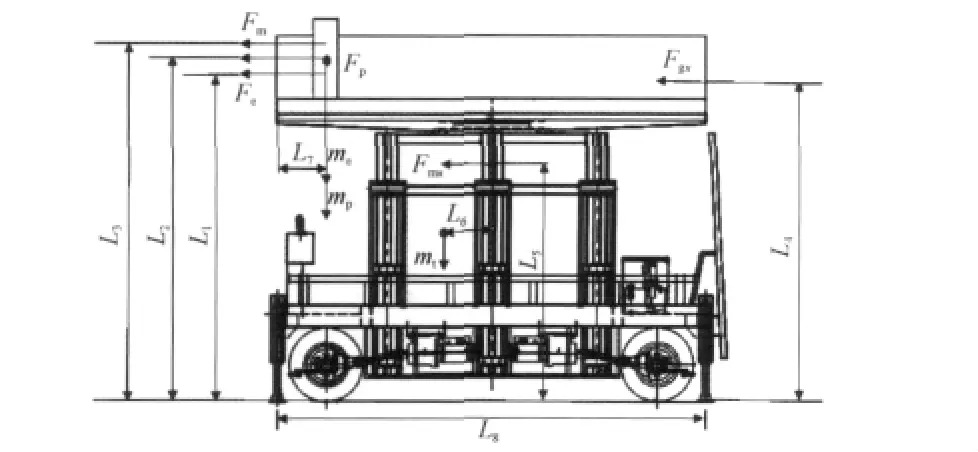
图5 平台横向受力分析示意图Fig.5 Diagram of platform transverse stress analysis
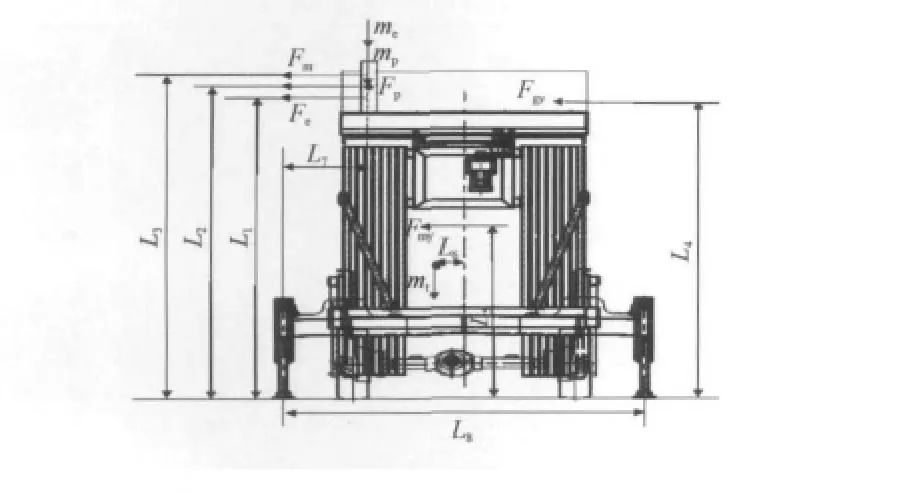
图6 平台纵向受力分析示意图Fig.6 Diagram of platform longitudinal stress analysis
倾覆力矩为
式中:Mt为倾覆力矩;Fe为作用在设备的风力;L1为风力设备作用点与地面之间的距离;Fp为作用在人身上风力;L2为工作人员的作用点与地面之间的距离;Fm为工作人员手操作力;L3为工作人员手操作力与地面之间的距离;Fgx为作用在平台和护栏上的横向风力;L4为风力在平台和护栏的作用点与地面距离;Fmx为作用在起升机构上的横向风力;L5为起升机构的作用点与地面之间的距离.
依据《GB3811—83起重机设计规范》,高空平台的稳定性安全系数K为
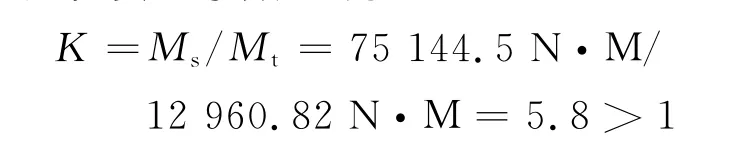
所以,在工况1条件下,平台横向是稳定的.
2.1.2 工况1下的平台纵向整机抗倾覆稳定性分析稳定力矩
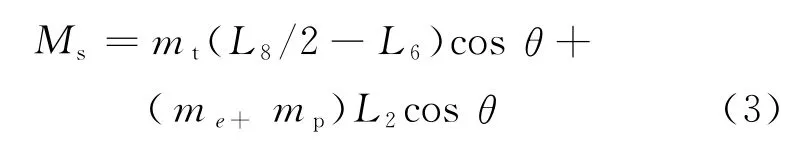
倾覆力矩为
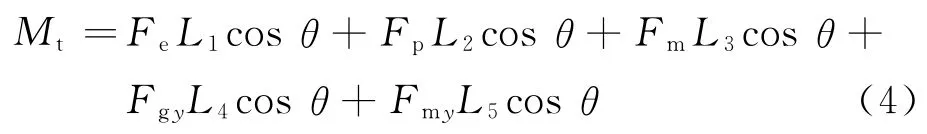
式中:Fgy为作用在平台和护栏上的纵向风力;Fmy为作用在起升机构上的纵向风力.
依据《GB3811—83起重机设计规范》,高空平台的稳定性安全系数K为
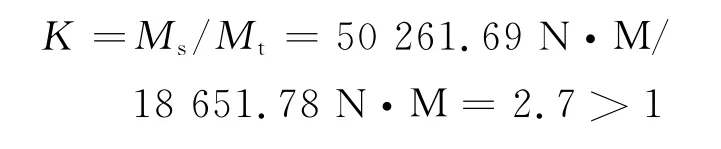
所以,在工况1条件下,平台纵向也是稳定的.
2.2 工况2抗倾覆稳定性模型求解
在工况2条件下,自行式高空作业平台横向和纵向的受力分析如图7,8所示.
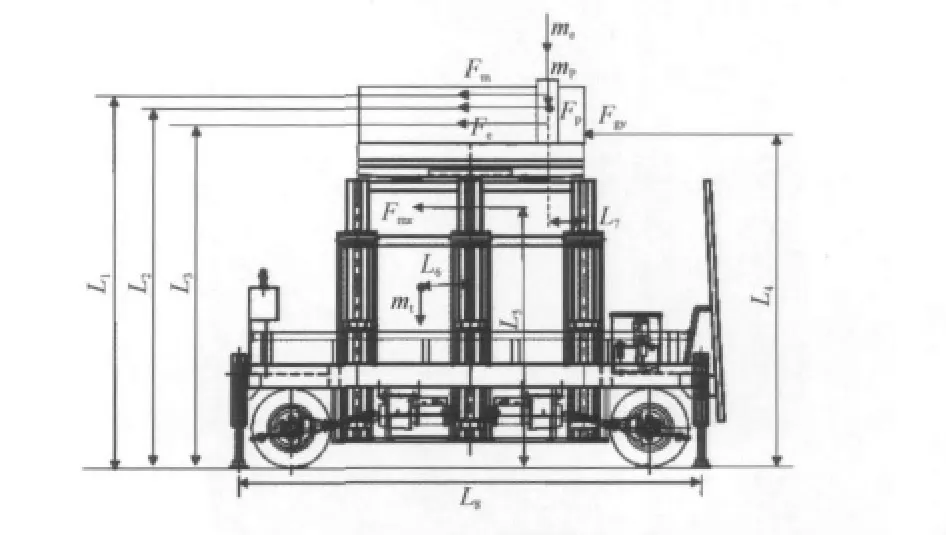
图7 平台横向受力分析示意图Fig.7 Diagram of platform transverse stress analysis
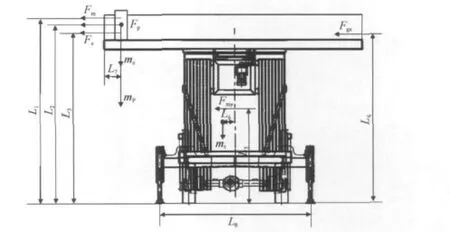
图8 平台纵向受力分析示意图Fig.8 Diagram of platform longitudinal stress analysis
利用力矩平衡法分别列出高空作业平台横向和纵向整机抗倾覆稳定性的数学模型.
2.2.1 工况2下的平台横向整机抗倾覆稳定性分析
稳定力矩为
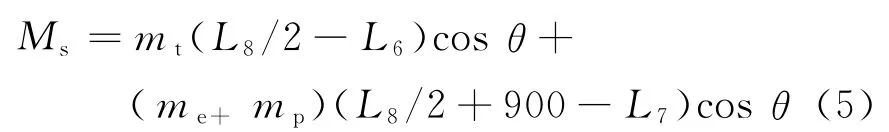
倾覆力矩为
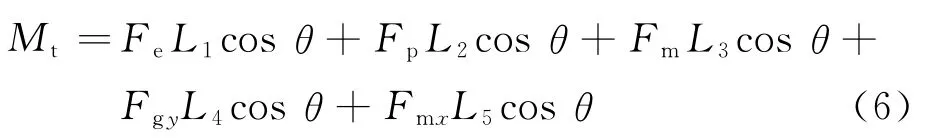
稳 定 性 安 全 系 数K=Ms/Mt=75 865.67N·M/14 679.19N·M=5.2>1,所以在工况2条件下,平台横向是稳定的,且有较大的安全储备.
2.2.2 工况2下的平台纵向整机抗倾覆稳定性分析稳定力矩为
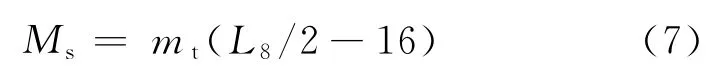
倾覆力矩为
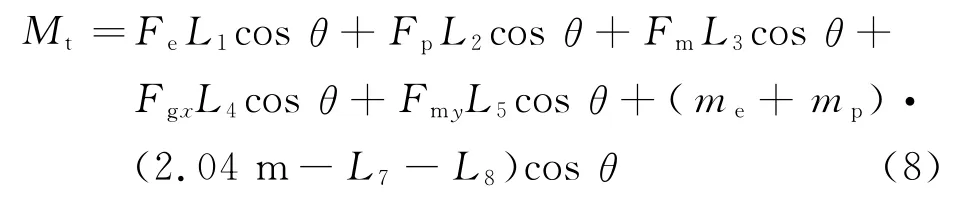
稳 定 性 安 全 系 数K=Ms/Mt=48 204.003N·M/19 343.843N·M=2.5>1,所以在工况2条件下,平台纵向也是稳定的.
3 起升机构局部稳定性的分析与计算
自行式高空作业平台采用桅柱式起升机构进行升降,各桅柱组主要由高强度铝合金型材、板式传动链条、链轮等组成,是升降工作平台的重要传动部件.因此其局部稳定性的好与坏,对保证施工安全、减少安全事故具有十分重要的意义.本文利用有限元分析软件ANSYS创建起升机构的APDL参数化模型[5],进行该起升机构的特征值屈曲分析[6].
3.1 建立起升机构有限元模型
考虑到铝合金6组桅柱的材料特性,本次分析选用Beam188梁单元来建立起升机构的有限元模型.Beam188是2节点的三维线性梁单元,每个节点有6个自由度,并能够承受拉、压、弯、扭特性;材料的弹性模量E=70GPa,泊松比λ=0.3,密度ρ=2.7t·m-3.网格划分后,起升机构有限元模型如图9所示,该模型共有462个节点,420个单元.

图9 起升机构有限元模型Fig.9 Finite element model of hoisting mechanism
3.2 起升机构特征值屈曲分析
对已建立的有限元模型施加约束和外载荷:限制起升机构底部6个节点的全部自由度及全耦合起升机构顶部6个节点的全部自由度,以更好模拟连接架与桅柱组的连接关系;对起升机构顶部6个节点施加竖直向下的外载荷(忽略风载荷影响);对起升机构施加竖直向上的重力加速度(g=9.8m·s-2),用惯性力来模拟其重力.然后打开预应力效果选项,进行静力学求解.然后利用Block Lanczos方法获得起升机构前10阶的屈曲特征值和屈曲模态[7-8].起升机构前10阶的屈曲特征值如表1所示.
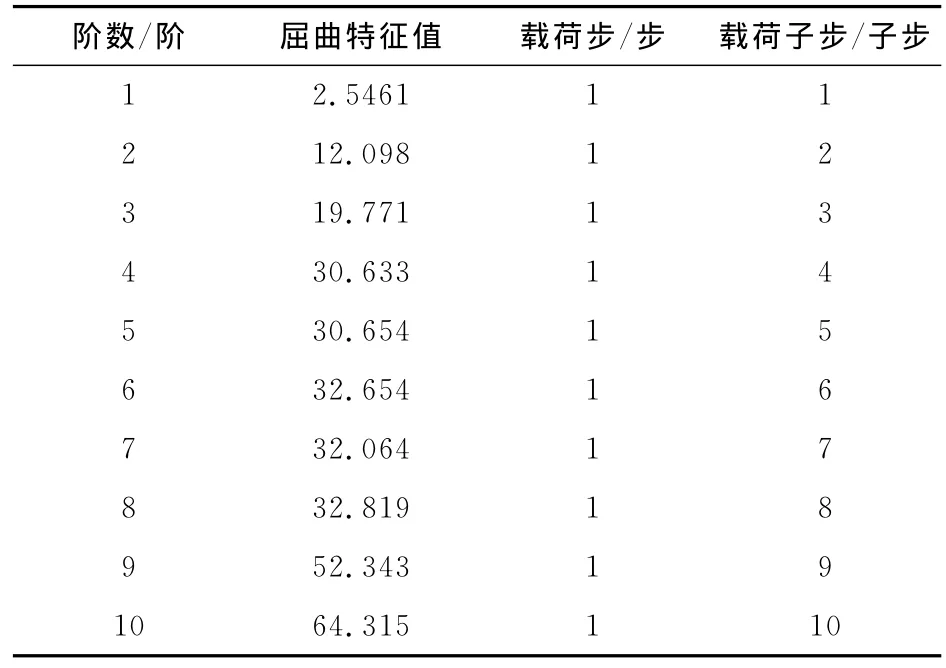
表1 升降机构前十阶的屈曲特征值Table 1 Former ten step buckling eigenvalue of hoisting mechanism
从表1可以看出:起升机构一阶屈曲特征值为2.546 1>1,则屈曲临界载荷为23 398.65N,这在实际应用中是比较安全的,不会发生屈曲破坏,起升机构具有很好的稳定性.
3.3 起升机构非线性屈曲分析
由于结构失稳很可能发生在线性屈曲之前,因此在实际问题分析中,需要引入缺陷进行非线性分析.非线性屈曲分析考虑了几何非线性和材料塑性这两种主要非线性因素,因此相对于特征值屈曲分析,其结果更加精确,更符合结构极限状态时的受力和变形性能,对实际工程的设计有一定的指导意义[9-10].
本文采用20个子步的加载方式,施加100%的偏位缺陷2.26mm,并把1.3倍线性屈曲载荷逐步加载到起升机构顶部6个节点上,进行非线性屈曲分析.并选取顶部节点299作为参考点,根据其载荷位移曲线来判别结构是否达到稳定临界状态.
参考点299的载荷位移曲线如图10-12所示.
可以看出,当载荷增加到19 000N时,起升机构将会发生失稳现象,与特征值屈曲分析相比,屈曲载荷有一定程度的下降,计算结果偏于安全.在该极限载荷的作用下,参考点299最大位移为Ux=90mm,Uy=-0.5mm,Uz=-0.16×10-5mm.
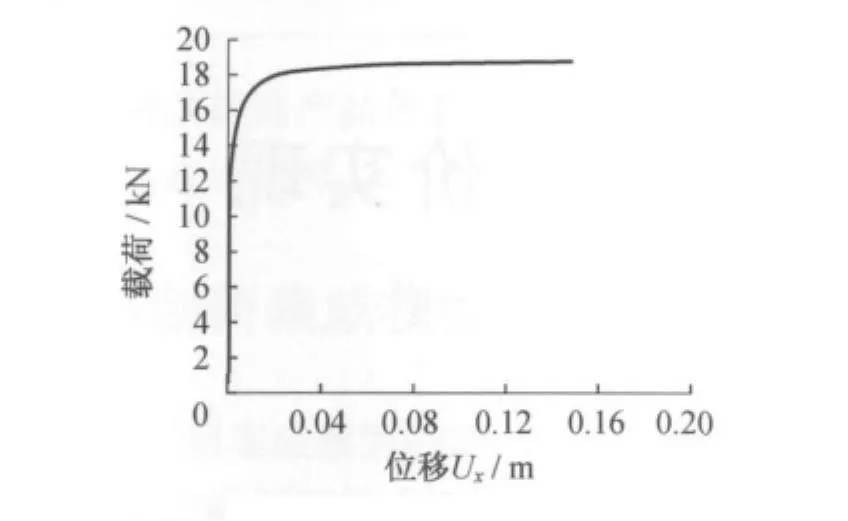
图10 x方向载荷-位移曲线Fig.10 x direction load-displacement curve
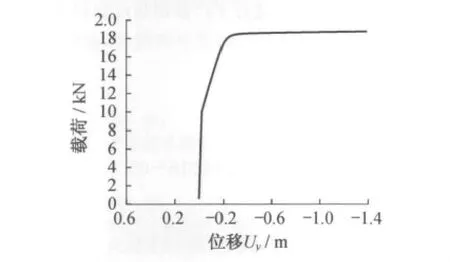
图11 y方向载荷-位移曲线Fig.11 y direction load-displacement curve
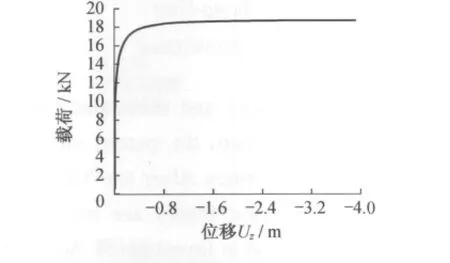
图12 z方向载荷-位移曲线Fig.12 z direction load-displacement curve
4 结语
本文应用力矩平衡法和有限元法,对自行式高空作业平台进行了整体和局部稳定性分析,得到如下结论:
(1)应用力矩平衡法建立高空作业平台抗倾覆稳定性数学模型,分析计算出两种危险工况下整机的稳定性情况.结果表明:在两种危险工况下,自行式高空作业平台是比较稳定的,不会发生倾翻.
(2)应用有限元法,对起升机构进行特征值屈曲分析,结果表明:该起升机构在工作状态下不会出现失稳现象,具有良好的稳定性.
(3)由于考虑了初始缺陷、塑性性能和大变形响应等因素的影响,非线性屈曲分析所得到的屈曲极限载荷要小于相同条件下的线性分析结果,计算值偏于安全,且有较大的安全余量.
[1]刘晓婷,赵洪亮,邢宇,等.高空作业平台抗倾覆稳定性分析[J].起重运输机械,2011(1):19-22.
LIU Xiaoting,ZHAO Hongliang,XING Yu,et al.Overturning-resistance stability analysis of aerial work platform[J].Lifting Transport Machinery,2011(1):19-22.
[2]谷礼新,郑海斌,彭卫平.塔式起重机起重臂结构和稳定性有限元分析[J].机电工程技术,2005,34(8):27-28.
GU Lixin,ZHENG Haibin,PENG Weiping.Tower crane boom structure and stability of finite element analysis[J].Electromechanical Engineering Technology,2005,34(8):27-28.
[3]刘鸿文.材料力学:I[M].第四版.北京:高等教育出版社,2008.
LIU Hongwen.Material mechanics:I[M].4th ed.Beijing:Higher Education Press,2008.
[4]梁淇洪.汽车起重机失稳分析与防范[J].机电工程技术,2007,36(5):100-102.
LIANG Qihong.Truck crane instability analysis and prevention[J].Electromechanical Engineering Technology,2007,36(5):100-102.
[5]龚曙光,谢桂兰,黄云清.ANSYS参数化编程与命令手册[M].北京:机械工业出版社,2010.
GONG Shuguang,XIE Guilan,HUANG Yunqing.ANSYS parameter programming and command manual[M].Beijing:China Machin Press,2010.
[6]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社,2012.
WANG Xinmin.ANSYS numerical analysis of engineering structure[M].Beijing:Public Transportation Press,2012.
[7]李萍.基于ANSYS的钢筋混凝土拱桥特征值屈曲分析[J].桥梁结构,2008(7):45-48.
LI Ping.The eigenvalue buckling analysis for reinforced concrete crane on arch bridge based on ANSYS[J].Bridge Structure,2008(7):45-48.
[8]屠凤莲,范顺成,罗文龙.基于ANSYS的支撑架特征值屈曲分析[J].河北工业大学学报,2010,39(3):6-10.
TU Fenglian,FAN Shuncheng,LUO Wenlong.The eigenvalue buckling analysis for support frame based on ANSYS[J].Journal of Hebei Industry University,2010,39(3):6-10.
[9]刘朝辉,柳翼,李轶鹤.ANSYS在结构稳定性中的应用[J].湖南工程学院学报,2002,12(2):33-35.
LIU Zhaohui,LIU Yi,LI Yihe.Application of ANSYS in structure stability [J].Journal of Hunan Institute of Engineering,2002,12(2):33-35.
[10]张晓霞,姚远.基于ANSYS机车牵引杆屈曲分析[J].计算机应用技术,2008,35(7):36-37.
ZHANG Xiaoxia,YAO Yuan.Buckling analysis for traction rod on locomotive based on ANSYS [J].Computer Application Technology,2008,35(7):36-37.
