基于流态化技术的振动流化床气固两相流动分析
2013-07-25柳洪义原培新
朱 亮,柳洪义,原培新
(东北大学 机械工程与自动化学院,辽宁 沈阳 110819)
褐煤是地球上分布最广泛的能源之一,是重要的能源和化工原料,我国的褐煤资源也比较丰富,目前已探明储量达1 303亿t.但因为存在含水量高(25%~50%),热值低等缺点,导致其市场价格较低,利用率低下,不仅浪费运力,且形成大量的燃烧废渣和由燃烧不充分所导致的空气污染.如将褐煤进行干燥并控制水分,就可以提升煤质(热值提升至14 000~20 000kJ),大大提高褐煤的市场用量和经济效益.
褐煤的干燥设备有滚筒干燥机、气流干燥机、流态化干燥机等多种类型.而振动流态化技术是将振动能量引入到普通流化床中,通过振动的加入使床层达到良好的流化状态的一种气固流态化技术,是目前国内褐煤干燥中最先进的也是最有发展前景的技术.因此,研究振动、风速、褐煤颗粒粒度等参数对振动流化床床层流态化的影响,对于开发大型振动流化干燥系统具有重要的意义.
本文根据Euler方法的双流体模型理论建立描述振动流化床气固两相流动的基本方程组,并在此基础上,建立振动流化床气固两相流动的动力学模型.采用专业的流体力学分析软件Fluent,通过用户自定义函数(UDF)编程加入振动作用对床层的影响,对褐煤颗粒床层进行数值模拟,通过对模拟结果进行对比分析,最终得出具有有效性和实用性的结论.
1 振动流化床气固两相流动的数学模型
1.1 气固两相双流体模型基本方程
Euler法的双流体模型能够较好地解决流化床中气固两相的流动问题,因此本文从振动流化床气固两相流动的物理本质着手,在双流体模型的基础上,建立振动流化床气固两相流动的数学模型[1].
气固两相的连续性方程
气相:
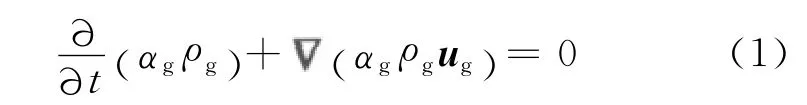
固相:
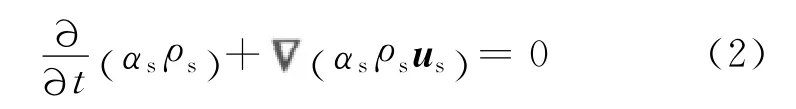
式(1),(2)中:αg,αs分别为气固两相的体积分数;为哈密顿算子;ug,us分别为气固两相的运动速度;ρg,ρs分别为气固两相的密度.
气固两相动量方程
由于气固两相间的升力和虚拟质量力相对于两相间的曳力来讲很小,可以忽略不计,因此气固两相流动的连续性方程和动量方程可简化为以下形式.
气相:
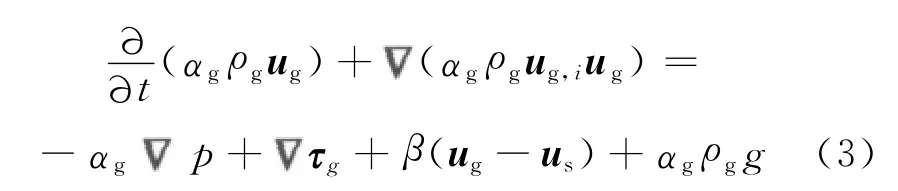
式中:ug,i为气相在x方向和y方向的运动速度,i=x,y;p为颗粒压力;τg为气相的剪切应力张量;β为气固两相间交换系数;g为体积分数.
固相:
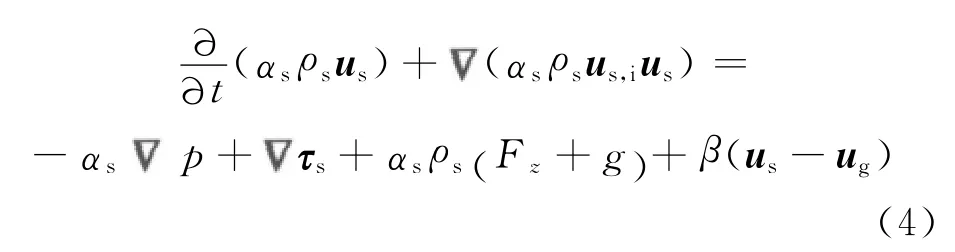
式中:us,i为固相在x方向和y方向的运动速度,i=x,y;τs为固相的剪切应力张量;Fz为振动流化床激振力.
1.2 曳力系数模型
气固两相间作用的曳力模型大致有三种:一种是根据实验数据关联所得到的经验或半经验模型,如 Gidaspow 模型[2],Syamlal-O'Brien模型[3];另一种是基于气固相作用的理论,通过纯数学方法推导出的模型,如 Koch-Hill模型[4];第三种是对经验或半经验模型进行修正的模型,如修正的Syamlal-OBrien模型[5],McKeen模型[6].Gidaspow 模型分别就气相体积份额的不同给出相应的气固两相间的曳力系数,有较广泛的运用范围,因此对于密集的气固流化床,相间曳力系数一般采用Gidaspow模型.本文即选择Gidaspow模型,具体形式如下:当αg>0.8时,气固两相间交换系数β为
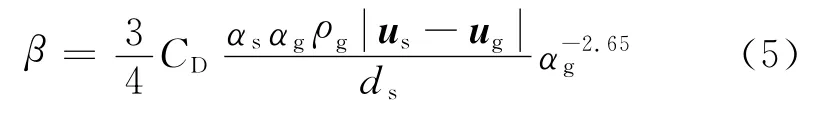
式中:CD为曳力系数;ds为颗粒直径.
当αg≤0.8时,气固两相间的交换系数为
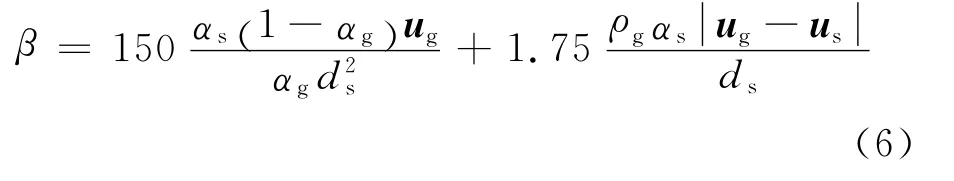
曳力系数为
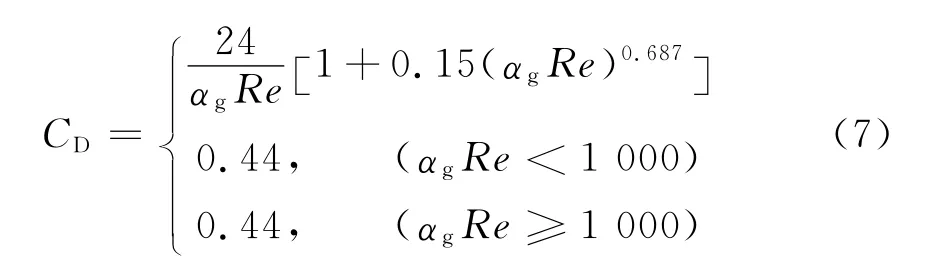
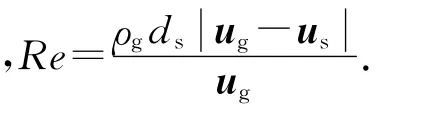
1.3 激振力的确定
肖帅刚等[7]测量了振动流化床中床层对分布板的作用力.当床层流化时,测得分布板与床层之间存在着连续的弹性作用,提出了分布板与床层间的弹性作用模型.模型中忽略颗粒床层内部轴径向的弹性差异,将弹性床层视为一个质量为m、弹性系数为k、阻尼系数为c的单自由度均匀弹性体,如图1所示.
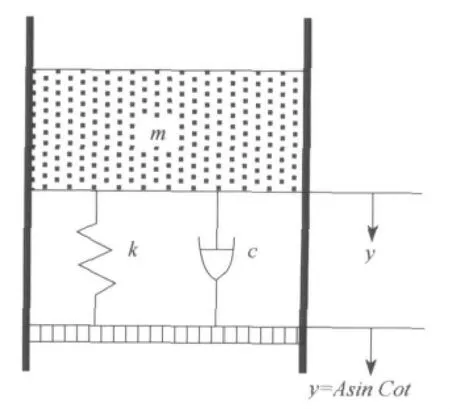
图1 振动流化床床层弹性模型示意图Fig.1 Vibrated fluidized bed’s bed flexibility model
分布板的运动方程为

式中:y为分布板的位移;A为振幅;ω为振动的频率;t为振动的时间.
取重力作用下的床层状态为平衡状态,不考虑流化床侧壁对床层的摩擦力,床层的受力为床层形变的弹性力和床层的阻尼力,则弹性床层的运动方程为
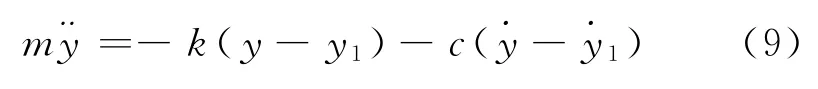
式中:y1为床层离开平衡状态的位移.
求解方程(9),可得流化床稳态解为
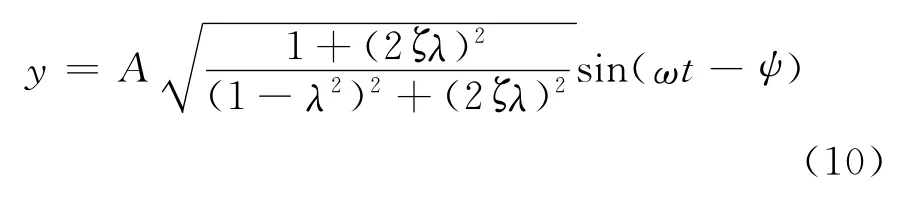
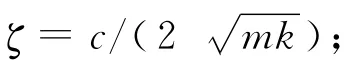
所以,分布板的受力F为
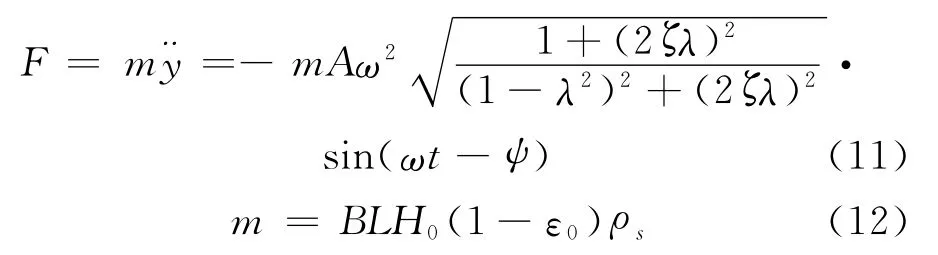
式中:B为床体的宽度;L为床体的长度;H0为床层的初始高度;ε0为床层的初始空隙率.
2 数值求解方法和物理参数的确定
2.1 数值求解方法
本文采用专业流体力学分析软件Fluent,并选取Euler双流体模型和气固两相流动的k-ε湍流模型.考虑模型中的振动作用,设定床体为正弦运动,网格划分为动态的层铺网格,且采用一阶迎风格式[8]的离散方法和压力-速度耦合的SIMPLE算法[9]进行迭代求解.
流化床的风由布风板底部吹入床体的,且一开始设定流化床入口处的气流速度为固定值,因此确定布风板气孔为速度入口型边界.而对床体壁面没有特殊要求,因此定义为壁面型边界.由于在正常工况下褐煤颗粒很难达到床体上部,并且在边界出口处有确定的静压,因此确定床体上部为压力出口型边界.
2.2 物理参数的确定
本文所研究的振动流化床,其主体部分尺寸:床体长度为19m,床体宽为3.6m,褐煤流化腔体高为3m,褐煤床层初始高度为0.24m.整个干燥系统的工艺流程如图2所示.
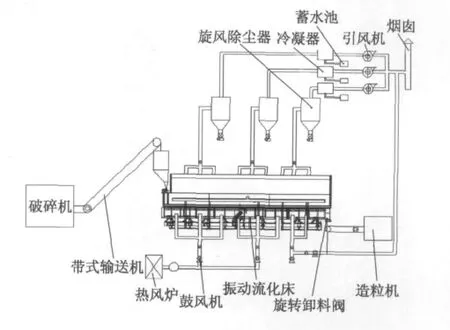
图2 150t·h-1褐煤干燥系统工艺流程图Fig.2 150t·h-1 Lignite dehumidification system process flow
根据已知条件的计算和相关物理模型的选择,可得振动流化床气固两相流动在Fluent中实现数值模拟所需要的物理参数,如表1所示.
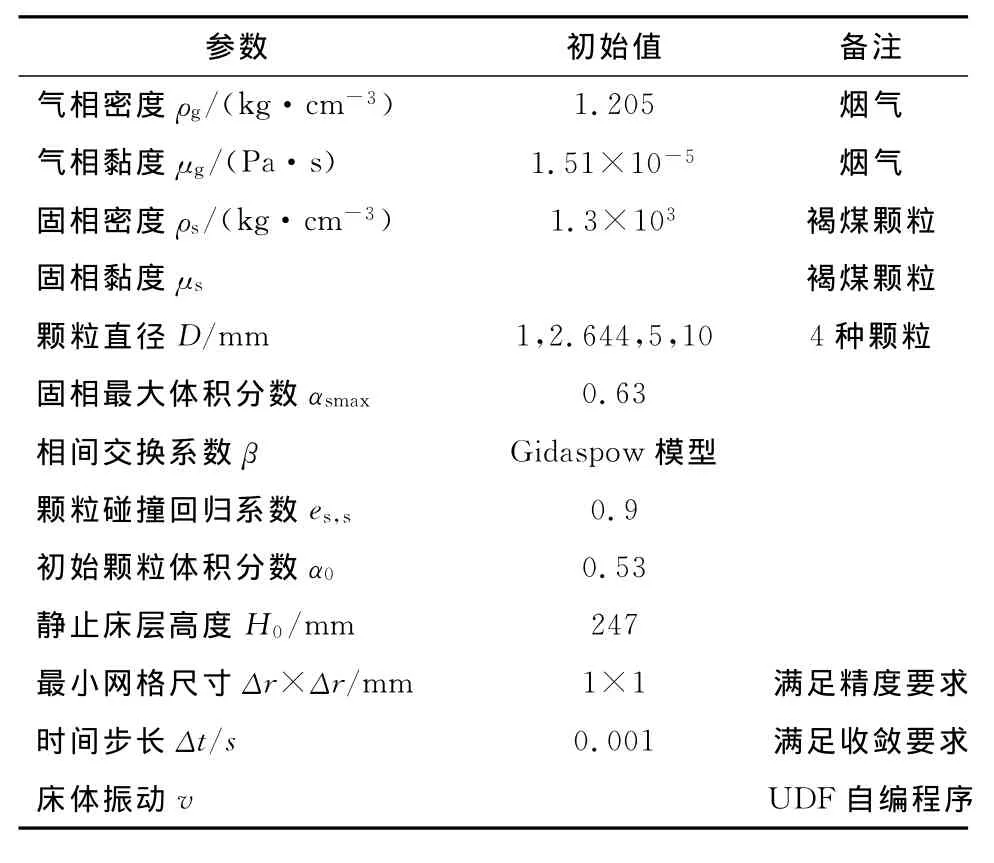
表1 模型中的参数及初始值Tab.1 Parameter and initial value in model
3 数值模拟结果及分析
3.1 振动对床层流化均匀性的影响
通过改变不同参数的大小如风速、振动频率等来对流化状态进行测试,得出相关的模拟结果.图3中,在不加振动时,普通流化床的气固两相流动杂乱无章,多处出现体积大且形状不规则的气泡.床层扰动非常剧烈,气固两相流动也非常不稳定.
从图4的压力等势线图中也可以看出,在不加振动时,等压线波动很大,床层压降分布不均匀,说明床层内气固两相流动杂乱而且扰动大.

图3 风速为1.5m·s-1、振频为0Hz时的体积分数图Fig.3 Volume fraction when air speed is 1.5m·s-1 and vibration frequency is 0Hz

图4 风速为1.5m·s-1、振频为0Hz时的压力等势线图Fig.4 Total pressure when air speed is 1.5m·s-1 and vibration frequency is 0Hz
从图3和图5的比较中发现,当有外加振动出现时,气固两相流动变得逐渐有序,气泡的生成受到了抑制,床层扰动得到了一定改善.但由于振动频率较低,激振力的作用不能使气泡完全消失,床层中仍有气泡存在.

图5 风速为1.5m·s-1、振频为10Hz时的体积分数图Fig.5 Volume fraction when air speed is 1.5m·s-1 and vibration frequency is 10Hz
随着振动频率的增大,如图6所示,可以明显地看出气泡的生成得到了进一步的抑制,气泡逐渐变小直至最终消失.这是因为床体垂直方向的振动在床层中产生了波动剪切作用,此作用挤压破碎了床层内部生成的气泡[10],故抑制了气泡的生成和长大,改善了气固两相接触和流化状态,使床层中气固两相的流动更加均匀稳定.

图6 风速为1.5m·s-1、振频为15Hz时的体积分数图Fig.6 Volume fraction when air speed is 1.5m·s-1 and vibration frequency is 15Hz
从图7和图8的压力等势线图的比较中也可以看出,随着振动频率的增加,等压线趋近于平行直线,床层压降分布均匀.风速为1.5m·s-1的情况下,当振动频率达到15Hz时,床层等压线已经基本平行于气体分布板,说明此时床层扰动很小,气固两相接触均匀稳定.

图7 风速为1.5m·s-1、振频为10Hz时的压力等势线图Fig.7 Total pressure when air speed is 1.5m·s-1 and vibration frequency is 10Hz

图8 风速为1.5m·s-1、振频为15Hz时的压力等势线图Fig.8 Total pressure when air speed is 1.5m·s-1 and vibration frequency is 15Hz
3.2 振动对床层颗粒返混现象的影响
图9中,风速为1.5m·s-1时,褐煤颗粒运动杂乱无章.床层剧烈的扰动和不稳定性,造成气体和颗粒并不是均匀沿床体轴向上升,而是出现了返混现象.颗粒的这种返混现象,会致使物料在床内滞留时间不同步,干燥后的颗粒含湿量不均匀,干燥效果较差,是在颗粒流化时需要注意的问题.

图9 风速为1.5m·s-1、振动频率为0Hz时颗粒速度矢量图Fig.9 Granule’s velocity vector when air speed is 1.5m·s-1 and vibration frequency is 0Hz
通过图9和图10、图11的对比,可以发现振动的加入有效抑制了床层的返混现象,且随振动频率的增大,这种抑制效果也越来越明显,气固两相流动更加均匀稳定.
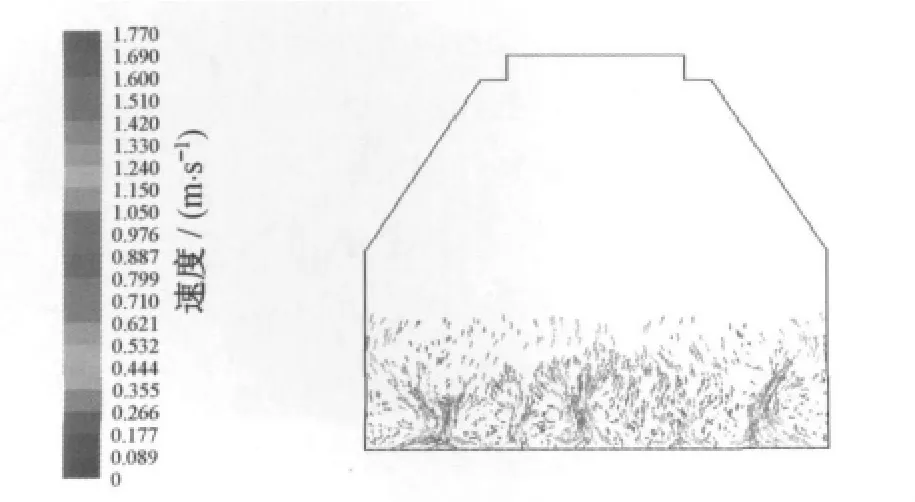
图10 风速为1.5m·s-1、振频为10Hz时颗粒速度矢量图Fig.10 Granule’s velocity vector when air speed is 1.5m·s-1 &vibration frequency is 10Hz
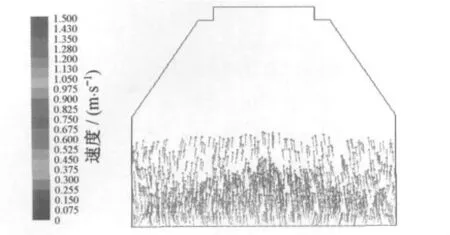
图11 风速为1.5m·s-1、振频为15Hz时颗粒速度矢量图Fig.11 Granule’s velocity vector when air speed is 1.5m·s-1 and vibration frequency is 15Hz
4 结论
振动对气泡的挤压和破碎作用,抑制了大气泡的生成,形成了高质量微泡甚至无泡流化状态,使得振动流化床床层扰动大大减小,床层中气固两相接触充分、流动均匀稳定.振动和气流的交互作用,可以有效抑制褐煤颗粒在床层中的返混现象,使得振动流化床褐煤颗粒干燥均匀.对在振动作用下的流化床进行数值模拟以及对模拟结果进行的分析,表明了选择双流体模型,并将Fluent流体力学计算软件用于振动流化床气固两相流动的数值模拟,是一种行之有效的数值模拟方法,有利于后续振动流化床参数的优化设定.
[1]林亮成,郑忠,陈伟,等.不同曳力模型对鼓泡床内气固两相流的模拟研究[J].化学反应工程与工艺,2010,26(5):390-398.
LIN Liangcheng,ZHENG Zhong,CHEN Wei,et al.A simulation study of gas-solid two phase flow in a bubbling fluidized bed with various drag force models[J].Chemical Reaction Engineering and Technology,2010,26(5):390-398.
[2]GIDASPOW D,TSUO Y D.Computation of flow patterns in circulating fluidized beds[J].AIChE Journal,1990,36(6):885-896.
[3]SYAMLAL M,O'BRIEN T J.Computer simulation of bubbles in a fluidized bed[J].AIChE Symposium Series,1989,85:22-31.
[4]KOCH D L,HILL R J.Inertial effects in suspension and porous-media flows[J].Annual Review of Fluid Mechanics,2001,33(3):619-647.
[5]ZIMMERMANN S,TAGHIPOUR F.CFD modeling of the hydrodynamics and reaction kinetics of FCC fluidized-bed reactors[J].Industrial & Engineering Chemistry Research,2005,44(26):9818-9827.
[6]MCKEEN T,PUGSLEY T.Simulation and experimental validation of a freely bubbling bed of FCC catalyst[J].Powder Technology,2003,129(1):139-152.
[7]肖帅刚,王亭杰,汪展文,等.振动流化床中浅床层时床层与分布板之间的弹性作用[J].过程工程学报,2001,1(2):132-137.
XIAO Shuaigang,WANG Tingjie,WANG Zhanwen,et al.Elastic interaction between the bed and the distributor in a vibrated fluidized bed[J].The Chinese Journal of Process Engineering,2001,1(2):132-137.
[8]郭宽良,孔祥谦,陈善年.计算传热学[M].合肥:中国科学技术大学出版社,1988.
GUO Kuanliang,KONG Xiangqian,CHEN Shannian.Computational heat transfer[M].Hefei:University of Science and Technology of China Press,1988.
[9]张凯,王瑞金,王刚.Fluent技术基础与应用实例[M].北京:清华大学出版社,2011.
ZHANG Kai, WANG Ruijin, WANG Gang.Fluent technology basic and instance application[M].Beijing:Tsinghua University Press,2011.
[10]骆振福,陈清如,陶秀祥.振动流化床的形成机理[J].中国矿业大学学报,2000,29(3):230-234.
LUO Zhenfu,CHEN Qingru,TAO Xiuxiang.Formation mechanism of vibrated fluidized bed[J].Journal of China University of Mining & Technology,2000,29(3):230-234.
[11]潘永康.现代干燥技术[M].北京:化学工业出版社,2002.
PAN Yongkang.Modern drying technology[M].Beijing:Chemical Industry Press,2002.
