基于移动平均位置不变性推论的NURBS曲线插补算法研究

宋 芳 郝双晖 郝明晖

1.上海工程技术大学，上海，201620 2.哈尔滨工业大学，哈尔滨，150001

0 引言

目前对参数曲线/曲面插补算法的研究多是基于Taylor展开发展起来的［1］。参数曲线的曲率是不断变化的，如何将加减速控制集成到曲线插补计算中，并实现加速度指令及位置对时间更高阶指令的连续，实现机床的高速、高精度加工，是数控技术研究者一直关注的重点和难点问题之一。

Yong等［2］提出了加速度控制的自适应插补算法，但该算法的加速度分布存在突变或跳跃，会给机床带来较大的冲击和振动，所以需考虑加加速度及更高阶指令在插补过程中的影响。Nam等［3］对上述算法进行了改进，加入了对进给加速度的实时监控，引入加速度控制，可以在一定程度上减小速度的波动。文献［4-5］建立了加减速限制模块，利用限制后的信息对曲线进行插补，但该算法只考虑了曲线的局部几何特征，当曲线曲率变化较快时，机床还是有可能因为来不及调整进给速度而出现过切(残留)现象。文献［6-7］将滤波技术引入到数控系统算法中，提出了基于滤波技术的NURBS曲线插补算法，实现了整个过程的加减速连续，但该算法没有考虑滤波处理后连接点及极值点的速度和位置会发生改变(这一改变将影响系统的加工精度)，并且该算法也未实现位置对时间更高阶指令的连续。

本文在以上研究的基础上，提出基于移动平均位置不变性的NURBS曲线插补算法。该算法通过对移动平均的位置不变性进行研究，推出位置不变性推论，并利用该推论得出对连接点和极值点的调整方法，使滤波前后的连接点及极值点的速度和位置不变，满足了加工精度要求。并且该方法具有可扩展性，可实现加速度或位移对时间更高阶指令的连续。

1 移动平均的位置不变性及推论

1.1 移动平均加减速控制算法基本原理

移动平均加减速控制算法的基本原理是，首先对直线加减速离散的速度进行移动平均处理，获得移动平均加减速控制算法的实际输出速度，然后对实际速度进行差分计算以获得实际输出加速度，最后利用梯形面积公式，求出实际输出的位置。这种方法获得的加速度曲线是连续变化的，可实现加减速阶段速度的平滑过渡。通过对此算法进行扩展可实现指令解释的高次可微分［8-9］。

1.2 位置不变性推论

位置不变性定理是指对直线加减速控制算法进行移动平均处理，处理前后的终点位置不变，该定理的证明参考文献［10］。根据移动平均算法及位置不变性原理推导出位置不变性推论。

推论 若以某插补点为中心，前后(n－1)/2(n为移动平均步数，且为奇数)个点的速度均等于该插补点的速度，则对其进行移动平均处理后，该点仍为被插补点，且该点速度与移动平均前该点速度相等。

证明 假设某指定插补点的移动平均前后速度曲线如图1所示。

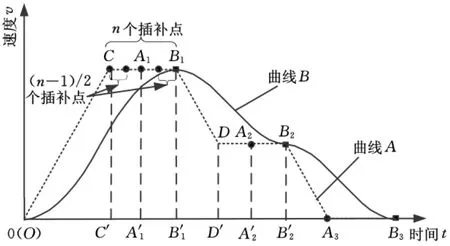
图1 指定插补点的移动平均前后速度曲线

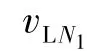
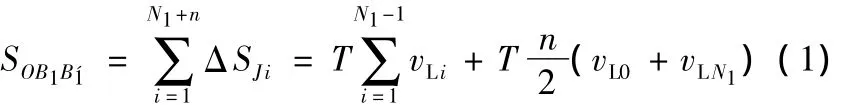
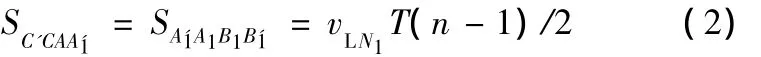
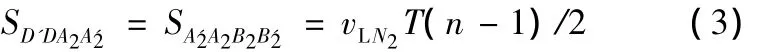
则有

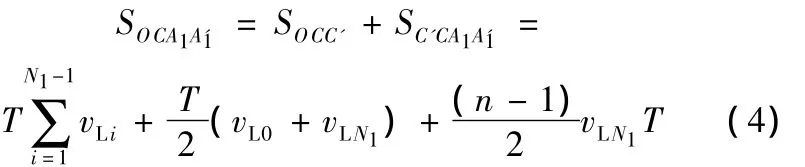
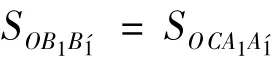
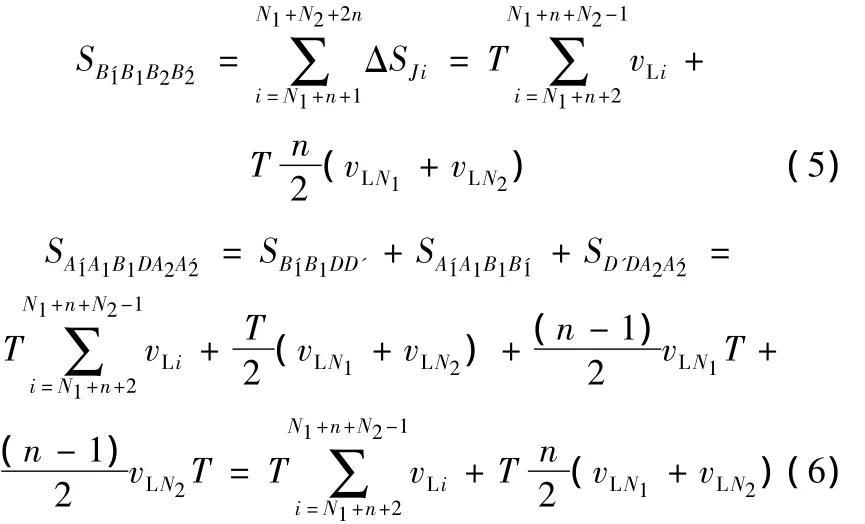
由上述证明可知，此推论成立。

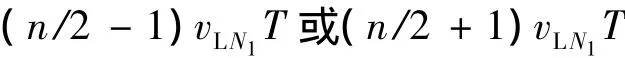
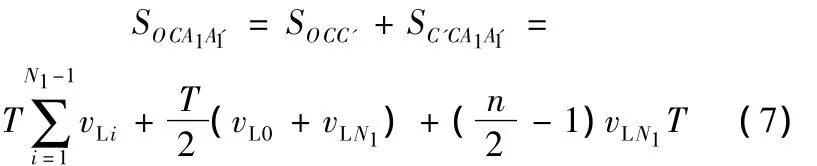
或

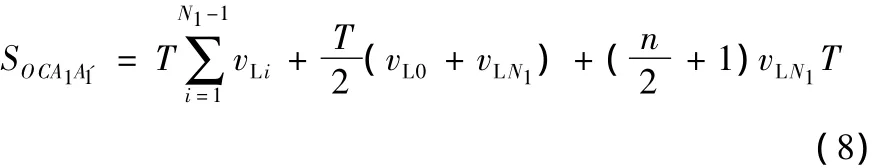
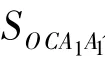
2 基于位置不变性推论的NURBS曲线插补

2个G代码之间的连接点和曲线的极值点(统称为指定点)是在实际插补过程中必须通过的点，这在采用其他加减速控制算法时是易于实现的。但采用移动平均加减速控制算法实现对被加工曲线的加减速控制，是对已规划好的直线加减速控制算法的速度进行移动平均处理，处理后的插补点将不通过指定点(不包括曲线的起始点和终点)。因此，利用位置不变性推论，对移动平均前的指定点附近插补点的速度、位置进行调整，可使移动平均处理后的插补点通过指定点，满足实际加工的要求，而不影响系统插补精度，其处理步骤如下:

(1)在进行预插补前，首先对曲线的几何特性进行分析，对影响进给速度的极值点曲率进行计算，并对进给速度进行分析。

(2)在对指定点附近插补点的进给速度和位置进行调整后，将曲线划分为多个区间，对各区间的速度分布类型进行研究，再确定各减速区间的减速点。

(3)最后利用直线加减速控制算法完成对NURBS曲线的一次预插补，然后利用移动平均对预插补结果进行处理，可实现加速度指令或更高阶指令的高次平滑及对NURBS曲线的高精度插补。

2.1 预插补处理

2.1.1 临界曲率计算

首先利用临界曲率［11］将曲率函数进行区间划分，然后对大于临界曲率的区间采用等间距节点矢量扫描方法，求取该区间的曲率极值点及其参数。具体实现步骤如下:

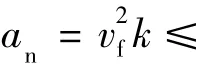
(2)曲率区间划分。所提出的基于临界曲率划分求取极值点曲率的方法，对区间边界参数的求解精度没有严格要求，即在进行曲率区间划分时，参数变化间距可以适当放大。

(3)求曲率区间的曲率极值点。由于对极值点曲率的求解精度有严格要求，因此采用等间距参数扫描方法求解时，为求得精确的极值点曲率，需要设置较小的参数变化间距。

2.1.2 进给速度分析

进给速度受弦高误差、向心加速度和加速过程中切向加速度限制，需满足以下条件:

(1)满足插补精度的最大进给速度为

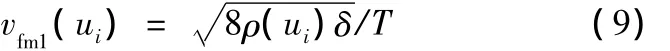
式中，ui为曲线的节点;ρ(ui)为节点ui的曲率。

(2)向心加速度许用的最大进给速度为

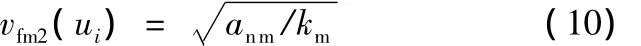
式中，km为当前曲率区间的曲率极大值。

(3)切向加速度许用的最大进给速度为

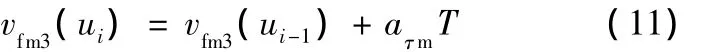
式中，aτm为最大切向加速度。

综上所述，进给速度除满足以上条件外，还需满足系统给定最大进给速度vf的限制，故各插补点的最大进给速度为

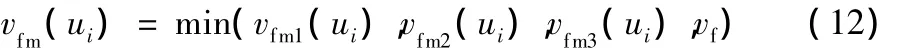
2.1.3 指定点附近插补点的速度和位置调整

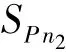
(1)沿加工方向的插补点处理。以连接点P为出发点，用vf进行预测，然后对最初的n2个点分别进行速度求解，所获得的最小速度为vP2min。

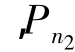
为使实际插补经过连接点P，故对连接点附近的插补点进行速度和位置调整，如图2所示。

一般来讲，极值点处的进给速度vPmin为半移动平均步数n2范围内插补点的最低速度，因此对这些插补点进行速度、位置的调整如图3所示。

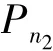
当进行多次移动平均处理实现指令解释高次可微分时，预测步数n2为各阶半移动平均步数之和。

利用各连接点或极值点附近匀速开始点的位置SPn2，将曲线划分为多段，采用等间距参数扫描方法可分别计算出各段的弧长，此时NURBS曲线被划分为Lseg1、Lseg2、Lseg3等多段，且各段的速度分布如图4所示。至此即可初步获取各区间的速度、位置及各区间终点的参数信息。

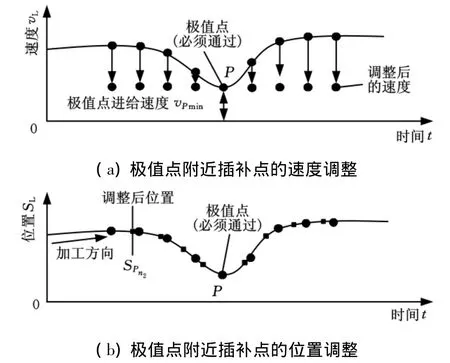
图3 极值点附近插补点的速度和位置调整示意图

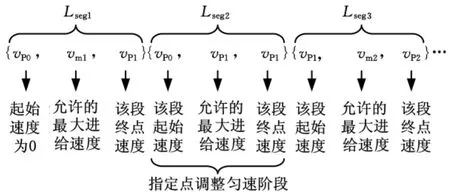
图4 调整后的速度分布图

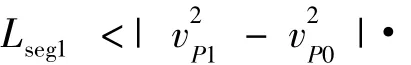
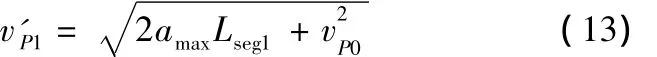
当vP1≤vP2时

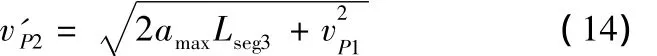
当vP1＞vP2时

…

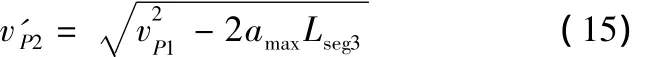
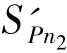
2.1.4 直线加减速控制的NURBS曲线预插补

通过以上处理，即可获得预插补处理过程中需要的各区间信息。下面首先利用这些信息确定速度分布类型，然后根据速度的分布类型，利用直线加减速控制算法确定减速距离，判断减速点，最后从减速点开始对速度分布进行进一步的精确计算，从而实现基于直线加减速的NURBS曲线预插补处理。

除匀速区域外，其他区域的起始速度和终点速度不一定相同，也就是说加速过程和减速过程不对称。速度的分布类型主要由各区间的弧长决定，下面将利用各临界状态弧长与各区间实际弧长之间的关系确定速度分布类型。

临界状态弧长是指以起始速度vs加速到终止速度ve所需的位移Sref1，即Sref1=SOAFG，以及能够达到指令进给速度所需要的最小位移Sref2，即Sref2=SOBEG+SBCDE，如图5所示。

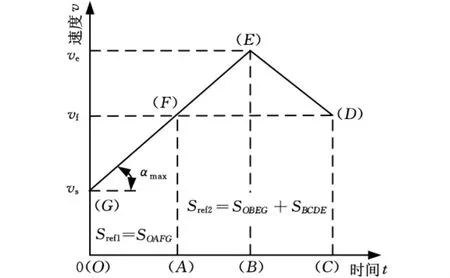
图5 临界状态速度曲线图

图5中，假设起始速度vs小于终止速度ve，即vs＜ve≤vf，amax为系统允许的最大加速度，则临界位移Sref1和Sref2的计算公式如下:

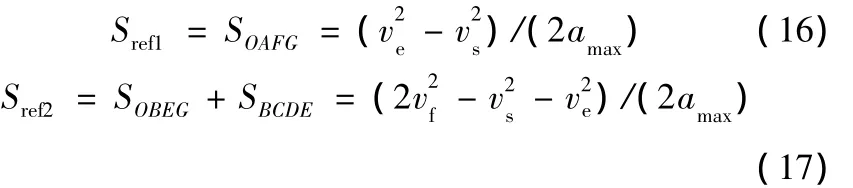
当ve≤vs≤vf时，速度曲线分布类型与vs＜ve≤vf情况的确定方式类似，本文不再赘述。

下面将通过各段弧长Lsegi与临界位移Sref1和Sref2的关系确定速度曲线的分布状态。

(1)Lsegi＞Sref2的情况。此时，速度可以达到系统的指令进给速度vf，因此速度曲线具有加速区、匀速区和减速区，具体情况如图6所示。其中，Lsegi=SOBEG+SBHKE+SHIJK。利用直线加减速控制算法的处理方式，很容易确定减速点及加速阶段的步数Na、匀速阶段的步数Ne及减速阶段的步数Nd，这里不再赘述。

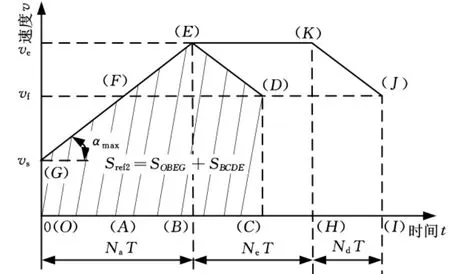
图6 达到指令进给速度v f时的速度曲线分布图

(2)Sref1≤Lsegi≤Sref2的情况。此种情况不能达到系统的指令进给速度vf，因此速度曲线仅具有加速区和减速区，具体情况如图7所示，其中，Lsegi=SOBNG+SBLMN。

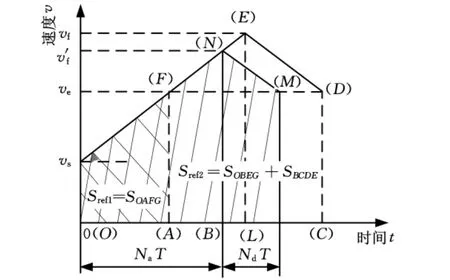
图7 未达到指令进给速度v f时的速度曲线分布图

设能够达到的最大进给速度为v'f，则有

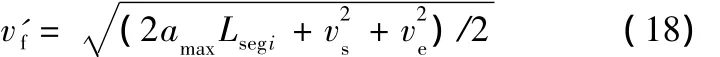
下面同样利用直线加减速控制算法的处理方式，很容易确定减速点及加速阶段的步数Na和减速阶段的步数Nd，这里不再对其进行赘述。

(3)Lsegi＜Sref1的情况。此种情况经过式(13)～式(15)的调整，已使Lsegi=Sref1，因此可按照情况2进行处理。

以上完成对速度分布类型的研究，再利用直线加减速计算公式可获得各离散点的插补速度和位置，即完成对NURBS曲线的预插补。

2.2 基于移动平均的NURBS曲线实时插补

通过以上研究实现了基于直线加减速控制的NURBS曲线预插补处理，但所获得的指令解释不具有高次可微分性，故需对经过直线加减速处理后获得的速度进行移动平均处理。

假设移动平均步数为N，前N－1个移动平均处理前的速度组成的数组为p［N－1］，将当前插补点移动平均处理前的速度vL(ui)代入到下式:

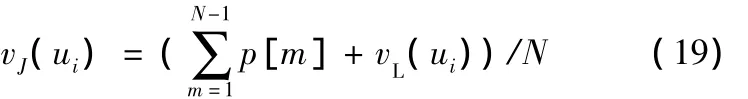
即可求得当前插补点移动平均处理后的速度vJ(ui)。

为实现指令解释的高次可微分性，利用多次移动平均进行处理，在式(19)的基础上对速度重复上述移动平均处理过程。则当前插补点移动平均后的加速度为

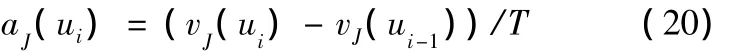
式中，vJ(ui－1)为上一插补点移动平均后的速度，m/s。

由于NURBS曲线在每一点处的弧长计算是非常复杂且耗时的，不适于在实时插补中使用，故采用将弧长近似为相邻插补点间直线段距离累加的方式来获取曲线起点至当前插补点之间的距离，其计算公式为

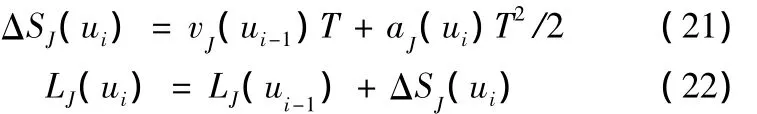
式中，ΔSJ(ui)为前一插补点与当前插补点之间的直线距离，m;LJ(ui－1)为曲线起点至前一插补点的距离，m;LJ(ui)为曲线起点至当前插补点的距离，m。

通过上述处理，即可实现基于移动平均的NURBS曲线实时插补，同时也完成了NURBS曲线指令解释的高次可微分。

3 实验验证

下面将以一条三轴加工的NURBS曲线路径为例，对所提出的NURBS曲线插补算法进行验证，该曲线路径如图8所示。

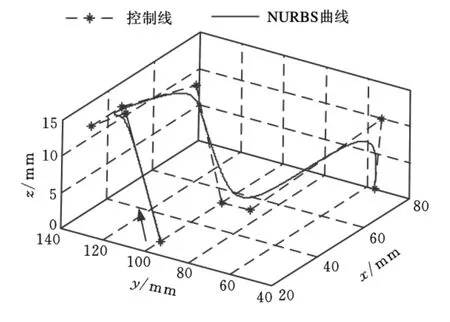
图8 NURBS曲线插补实例

曲线参数如下:控制点为(26.7，100.0，0)，(35.1，126.3，14.0)， (35.1，133.3，13.3)，(40.0，133.3，13.3)， (60.0，120.0，13.3)，(53.3，100.0，10.0)， (53.3，86.7，0)， (80.0，53.3，10.0)，(80.0，56.7，0)mm;节点矢量 U=(0，0，0，0，0.3，0.4，0.6，0.7，0.8，1.0，1.0，1.0，1.0);权值W=(1.0，4.0，0.5，1.0，3.0，0.8，2.0，6.0，4.0)。

取机床许用的最大加速度amax=5m/s2，T=60μs，vf=0.2m/s，δ=1μm，一次及二次移动平均步数n=n'=65。

3.1 直线加减速控制的预插补

对极值点附近插补点的位置、速度进行调整后，即可获得直线加减速预处理的速度、加速度曲线和加加速度曲线，如图9所示。

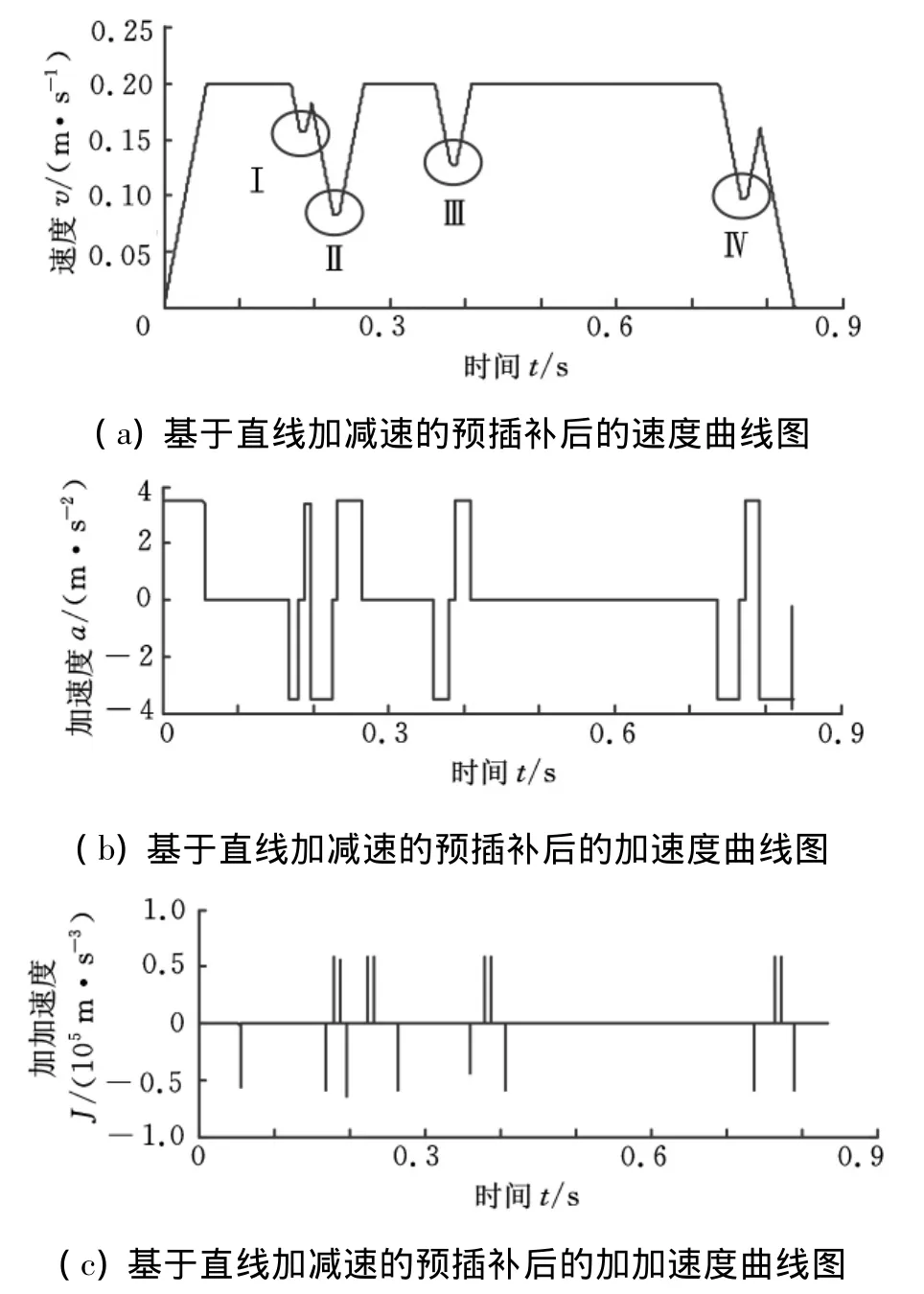
图9 调整后的直线加减速预插补控制曲线图

图9a中，标记的Ⅰ～Ⅳ表示调整后的4个匀速区间，除此之外，其他各区域速度根据曲率变化自适应调整。但由图9所获得的直线加减速控制曲线中，加速度曲线不连续，速度变化时将会产生冲击和振动。

3.2 二次移动平均处理实时插补

下面基于直线加减速预插补处理结果对离散后的速度进行二次移动平均处理，实现对NURBS曲线指令解释的高次可微分。该条NURBS曲线的速度、加速度、加加速度、位移的4次微分及位移的5次微分仿真结果如图10所示。

由图10可知，二次移动平均处理能实现速度曲线平滑以及加速度、加加速度曲线的连续。更重要的是，可实现对NURBS曲线指令解释的4次微分处理。

图10 二次移动平均处理实时插补曲线图

移动平均前后的速度及极值点附近速度放大图，分别如图11、图12所示。

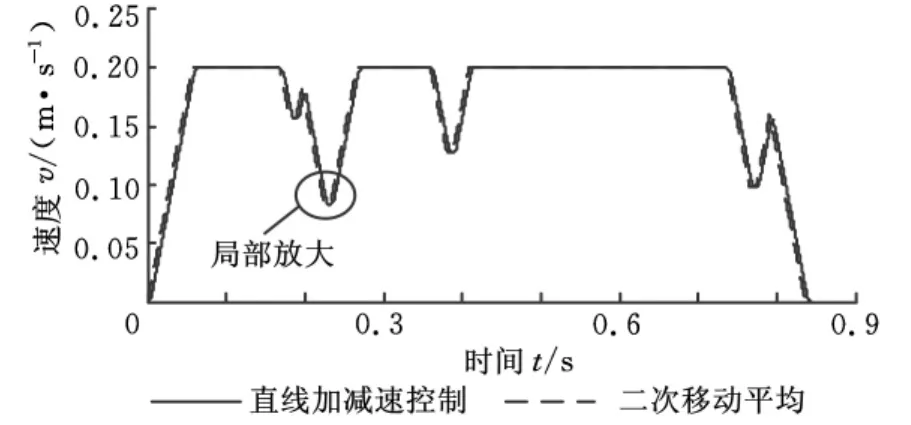
图11 移动平均前后速度比较图

由图12可知，对极值点附近插补点的速度和位置调整处理后，移动平均前后的极值点速度没有改变，将不会影响系统的插补精度。

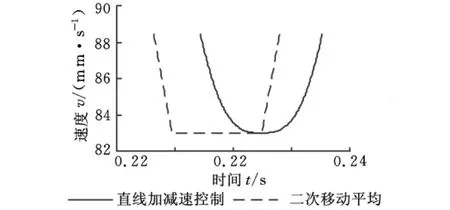
图12 极值点附近速度放大图

4 结语

本文提出了移动平均位置不变性推论，利用该推论对移动平均指定点附近插补点的速度、位置进行调整，使移动平均处理后的插补点通过指定点，将进给速度加减速控制集成到曲线插补中，能实现加速度及更高阶指令的连续。实例证明了所提出算法的可行性和有效性。

［1］Yeh SS，Tu M F.A Novel Approach to the Design of NURBS Interpolator for Advanced Motion Systems［C］//Proceedings of the 2005 IEEE International Conference on Mechatronics.Taipei，2006:388-393.

［2］Yong T，Narayanaswami R.A Parametric Interpolator with Confined Chord Errors，Acceleration and Deceleration for NCMachining［J］.Computer－ Aided Design，2003，35(13):1249-1259.

［3］Nam SH，Yang M Y.A Study on a Generalized Parametric Interpolator with Real－time Jerk－limited Acceleration［J］.Computer － Aided Design，2004，36(1):27-36.

［4］Lin M T，Tsai M S，Yau H T.Development of Realtime Look－ahead Algorithm for NURBS Interpolator with Consideration of Servo Dynamics［C］//Proceedings of the 46th IEEE Conference on Decision and Control.New Orleans，LA，USA，2007:1862-1867.

［5］Shi X G，Xu B G，Xie W，et al.Design and Implementation of S－shape Acceleration/Deceleration Algorithm Based on Rounding Error Compensation Tactic［C］//Proceedings of the 7th World Congress on Intelligent Control and Automation.Chongqing，2008:7912-7916.

［6］张晓辉，于东，胡毅，等.基于滤波技术的NURBS曲线插补算法研究［J］.中国机械工程，2009，20(14):1695-1699.

Zhang Xiaohui，Yu Dong，Hu Yi，et al.Research on NURBS Interplation Algorithm Based on Filtering［J］.China Mechanical Engineering，2009，20(14):1695-1699.

［7］董伯麟，王治森，韩江.高速高精度加工中NURBS曲线混合插补算法［J］.农业机械学报，2008，39(6):174-178.

Dong Bolin，Wang Zhisen，Han Jiang.NURBS Curve Hybrid Interpolator in High Speed and High Accuracy Machining［J］.Transactions of the Chinese Society for Agricultural Machinery，2008，39(6):174-178.

［8］Song F，Hao SH，Hao M H，et al.Research on Acceleration and Deceleration Control Algorithm of NC Instruction Interpretations with High－order Smooth［C］//International Conference on Intelligent Robotics and Applications.Wuhan，2008:548-557.

［9］郝双晖，宋芳，郝明晖，等.移动平均加减速控制算法的研究［J］.东北大学学报(自然科学版)，2008，29(增1):222-225.

Hao Shuanghui，Song Fang，Hao Minghui，et al.Research on Acceleration－deceleration Control Algorithm Based on Moving Average Method［J］.Journal of Northeastern University(Natural Science)，2008，29(S1):222-225.

［10］于东，胡韶华，盖荣丽，等.基于滤波技术的数控系统加减速研究［J］.中国机械工程，2008，19(7):804-807.

Yu Dong，Hu Shaohua，Gai Rongli，et al.Research on Acceleration and Deceleration for CNCMachine Tools Based on Filtering［J］.China Mechanical Engineering，2008，19(7):804-807.

［11］刘可照，彭芳瑜，吴昊，等.基于机床动力学特性的NURBS曲线直接插补［J］.机床与液压，2004(11):26-31.

Liu Kezhao，Peng Fangyu，Wu Hao，et al.An Interpolator for NURBS Curve Machining Based on Dynamical Characteristic of Machine［J］.Machine Tool＆ Hydraulics，2004(11):26-31.