基于任务的数控机床加工过程可靠性建模技术研究

王国强 张根保 洪 涛 陈家焱

1.中国计量学院，杭州，310018 2.重庆大学，重庆，400030

0 引言

在数控机床的众多指标中，用户对数控机床的可靠性指标的要求极高。数控机床不可靠，高性能不能维持，则会失去其可用性。因此，可靠性技术已成为我国数控机床发展的瓶颈，提高国产数控机床的可靠性水平已成为行业的一致呼声［1-2］。

早在20世纪70年代，前苏联的金属切削机床科学试验研究院在参数故障模型、工艺可靠性及可靠性预测等方面对机床可靠性进行了专门的研究，同时出版了论述数控机床精度与可靠性的专著［3-4］。Jia 等［5-6］在数控机床的可靠性设计、分析和评价方面的取得一系列的成果;张根保等［7-8］从全寿命周期的可靠性保证技术方面对数控机床的可靠性进行了研究。由于数控机床结构的复杂性，因此可靠性框图和故障树方法没有在数控机床的可靠性研究上取得较好的效果［9］;张强等［10］将功能元法引入到数控机床的可靠性研究中，提出了基于功能元法的数控机床功能信息和可靠性信息的抽象方法，建立了基于功能元法的可靠性模型，但该模型是一个静态模型，不能反映数控机床加工过程的可靠性变化特性;杨兆军等［11］建立了数控机床故障发生时间与各次故障发生时间的可靠性模型，但该模型不能反映数控机床加工过程某时刻的具体可靠度。

综上可知，目前对数控机床可靠性建模研究存在着“三多三少”的情况:①对数控机床零部件的可靠性建模的研究多，对整机可靠性建模的研究少;②对数控机床“静态”可靠性建模技术的研究多，对“动态”可靠性建模的研究少(数控机床加工零件的过程是个动态过程，可靠性建模必须与数控机床加工零件的实际相结合);③对数控机床单阶段任务可靠性建模的研究多，对多阶段系统任务可靠性建模的研究少。为了能够建立一个真实反映数控机床加工过程的动态可靠性模型，本研究引入数控机床元任务的概念，提出了元任务的分解模型，并建立了基于任务的数控机床加工过程可靠性模型，为数控机床的可靠性研究提供了一种可行的方法。

1 数控机床的任务分解

1.1 元任务的提出

任务可靠性研究的一般程序是先构建任务剖面，再明确关键故障的判定依据，紧接着分析设备的功能关系，最后采用一定的建模方法完成建模。数控机床具有任务周期长、任务形态随机多变的特点，这导致数控机床加工零件的任务剖面难以构建，故传统的方法无法反映数控机床实际的任务规律与特点。

科学研究方法表明，对于复杂的系统，必须先对其进行分解，将其分解为最基本的单元，通过对基本单元的分析研究达到化繁为简的目的。对于数控机床可靠性的研究也一样，虽然数控机床加工零件的过程复杂且带有明显的随机性，但其组成部分却可以分解成多个相对独立的元任务事件;虽然数控机床加工零件的总任务剖面难以构建，但元任务剖面却相对容易构建。为此，笔者从元任务的粒度来进行数控机床加工任务的可靠性研究。

1.2 元任务的定义

元任务是指数控机床执行加工零件的过程中能实现一定的目标或达到一定目的的最小结构单元［12］。数控机床刀库交换门开关任务所对应的设备有交换门、导轨、感应开关、气体管路、气源接口等，各设备之间的功能关系是固定的。就数控机床加工过程而言，数控机床刀库交换门开关任务不可再分，可见，刀库交换门的开关任务是一个元任务。

从元任务的定义，可知元任务具有以下性质［12］:

(1)有限性。独立成功实行该单元任务后，能够达成有限的任务目标。

(2)相对独立性。元任务执行时相对独立，与其他任务的联系较少。

(3)不可再分性。元任务的划分必须具备不可再分性，如果元任务还可再分，则其任务剖面的建立仍较麻烦，这将给总体任务的分析及模型的建立带来困难。元任务所对应的系统(设备)功能是相对固定的，任务目标相对明确，元任务执行的状态也能够完全确定，即要么成功，要么失败。

多个元任务的组合可以完成更大的任务目标或达到更大的目的，我们称之为元任务组。数控机床加工零件的总任务就是由这些元任务和元任务组组成的。因此，我们可以得到数控机床加工零件总任务的结构，如图1所示。

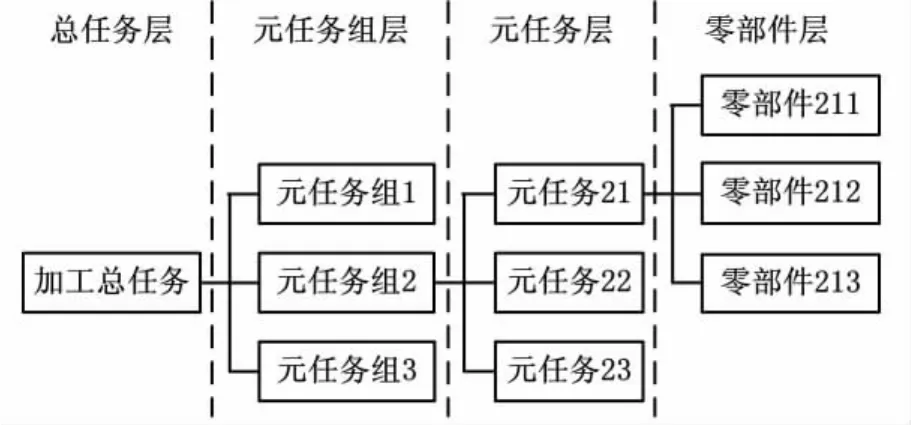
图1 数控机床加工零件总任务结构图

1.3 数控机床任务剖面的建立

数控机床加工过程可靠性模型建立的首要条件就是任务剖面的建立。由前文可知，传统的任务剖面难以反映数控机床任务复杂、随机变化的特点，因此，本文将其总任务剖面进行分解，建立图2所示的多层次任务剖面［12］。

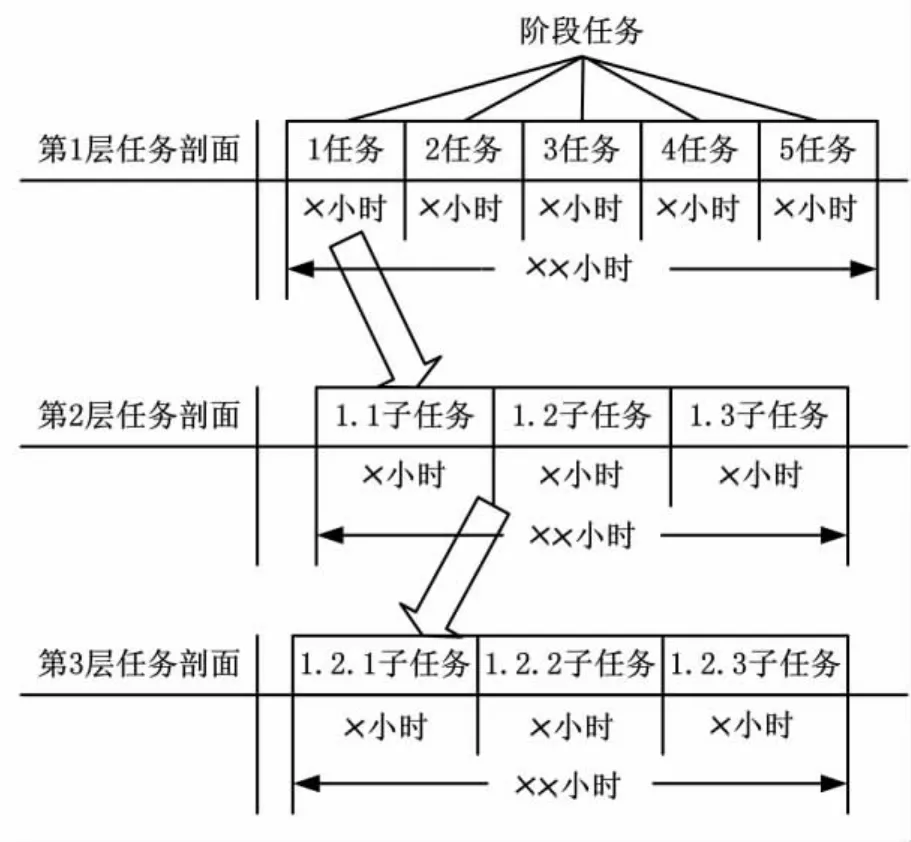
图2 数控机床任务剖面图

第1层次为数控机床总任务剖面，即总任务执行过程中要经历5个阶段。5个阶段为总任务的5个子任务，所以我们将5个阶段称为阶段任务，即任务剖面由阶段任务组成。每个阶段任务有自己的任务剖面，如任务1的任务剖面由第2层次“1.1子任务、1.2子任务、1.3子任务”三个阶段任务组成。1.2子任务剖面由第3层次“1.2.1子任务、1.2.2子任务、1.2.3子任务”三个阶段任务组成。这里需要说明的是，最底层的子任务肯定是元任务，中间层次的子任务可能是元任务，也可能是元任务组。

通过改进的任务剖面及必要的说明就可以清楚地了解数控机床任务过程的整体情况，也就做好了建立数控机床任务可靠性模型的准备。

2 数控机床元任务的可靠性建模

2.1 数控机床总任务的分解

由前文可知，对数控机床的加工过程进行建模必须放在元任务的粒度进行。为了达到这一目的，就必须采用1.3节中的思路，按照“总任务－元任务组－元任务”的结构化分解方法将加工总任务分解到元任务。

国产某型卧式加工中心是四轴四联动设备，在工件一次装夹后，可完成钻、镗、铰、攻丝、铣和轮廓的粗精加工。在加工过程中，能够实现刀具、工件的自动交换。该型卧式加工中心由床身系统(包括X轴、Z轴传动系统)、立柱系统(包括Y轴传动系统)、主轴箱系统、工作台系统(包括 B轴)、换刀系统、托盘交换系统、电气系统和辅助系统(液压系统、气动系统、冷却系统、润滑系统、排屑系统和防护装置)共13个分系统组成。

我们按照元任务组的分解方法将该型卧式加工中心的总任务进行分解，得到树形任务剖面图(图3)，各编号对应的元任务和元任务组如表1所示。

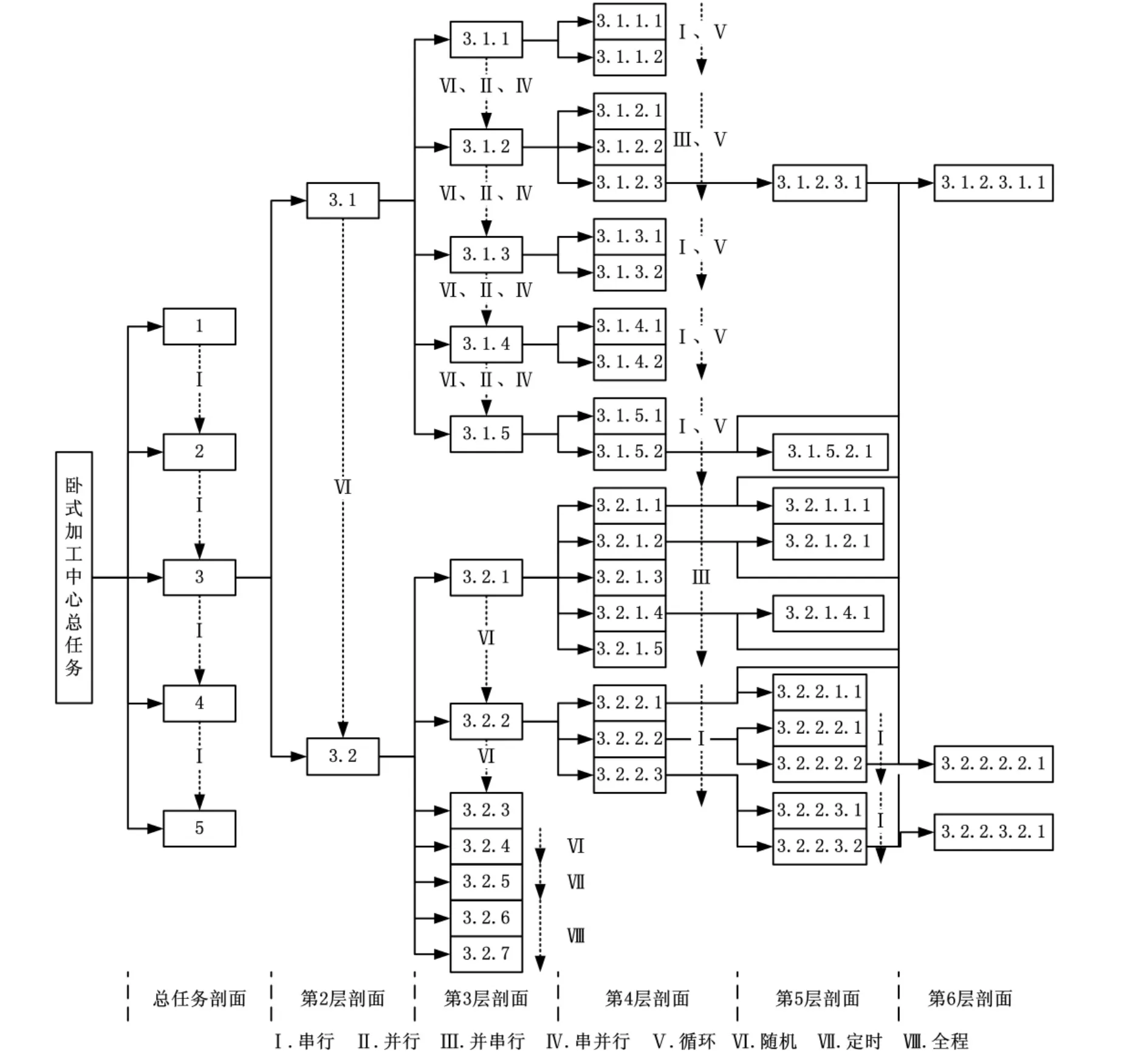
图3 卧式加工中心树形任务剖面图

2.2 数控机床元任务的建模

各元任务的组成不同，执行时间和次序也不同，所以必须对各元任务分别建模。传统的串并联模型起源于电子产品，并不完全适合于机械系统，对于机械产品而言，“相关”是其失效的普遍特征，如果忽略了系统中各零部件之间的相关性或忽略了某个零部件的多个失效模式之间的相关性，而简单地在失效相互独立的假设下进行零部件和系统的可靠性分析和计算，势必会导致过大的误差，甚至得出错误结论。因此，只有在考虑了数控机床各零部件之间相关性的情况下，建立的数控机床可靠性模型才更准确。研究发现，数控机床零部件的各种相关性主要发生在各零部件执行某项任务时，所以我们必须以任务为载体来研究这种相关性。成功流(goal oriented，GO)［13］方法的一个重要特点是能够真实反映机械系统逻辑进程上的相关性，因此本文采用GO法建立了数控机床各元任务的可靠性模型。

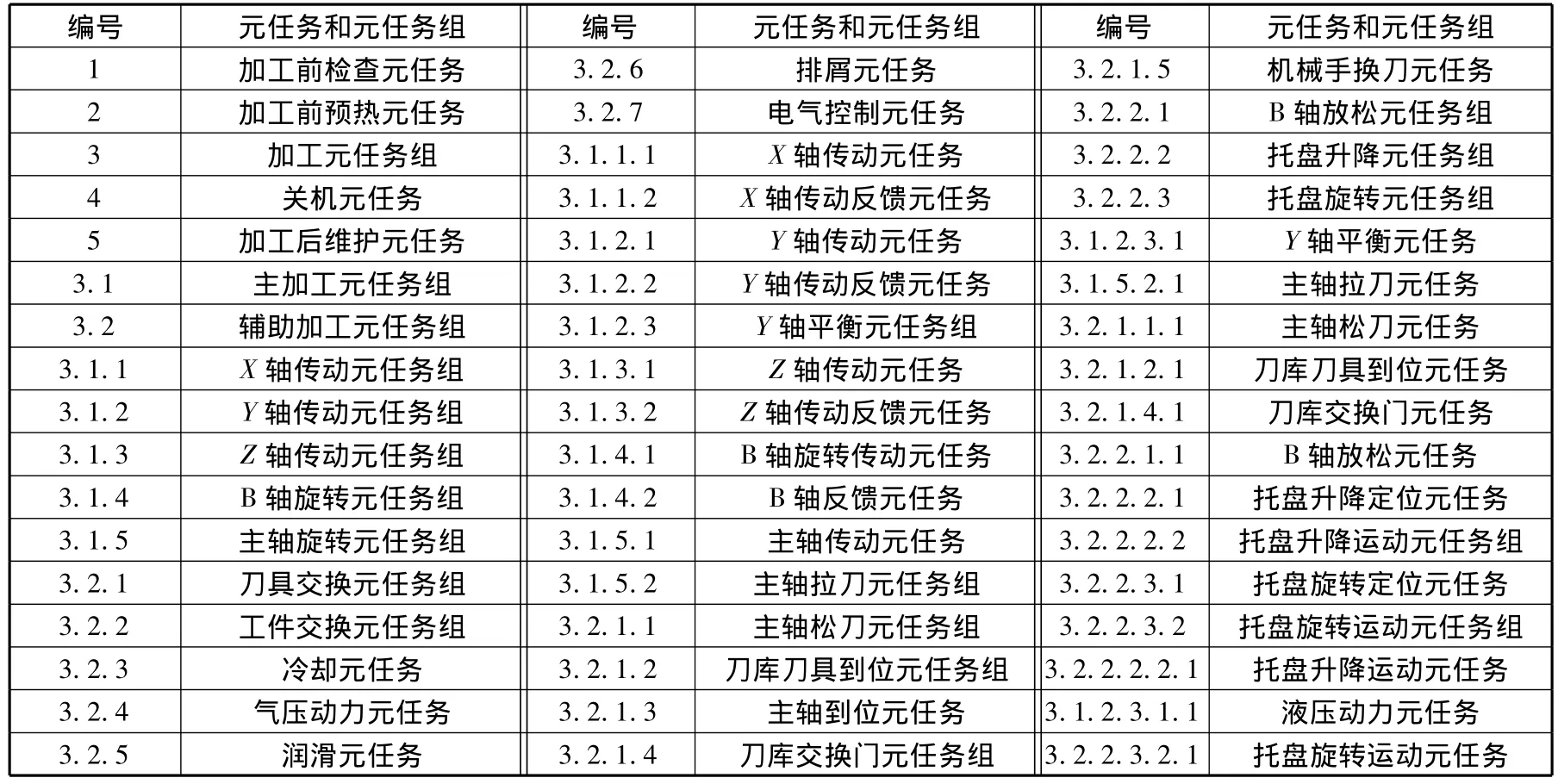
表1 编号及其对应的元任务和元任务组

按照GO法原理建立的数控机床元任务级动态可靠性模型为

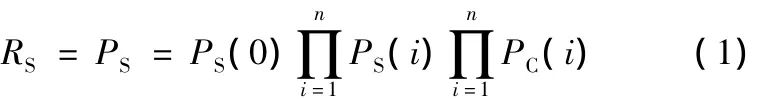
式中，RS为元任务的可靠度;PS为元任务成功完成执行的概率;n为组成元任务的零部件个数;i为组成元任务的零部件的编号;PS(0)为元任务输入的可靠度;PC(i)为组成各元任务的零部件本身的可靠度;PS(i)为控制信号的可靠度。

式(1)变换后可得元任务最终可靠度表达式:

式中，Ri为组成各元任务各零部件本身的可靠度。

采用上面的方法，我们可以得到图3中托盘升降元任务、托盘旋转元任务和液压动力元任务的动态可靠性模型:

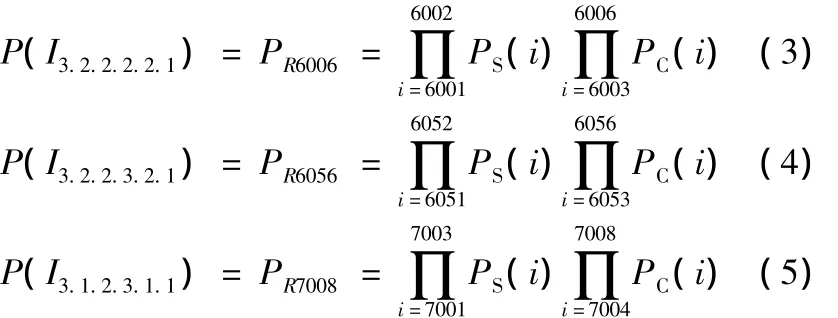
同理，我们同样可以得到图3中其余所有元任务的可靠性模型，在此不再一一赘述。

3 数控机床元任务组的可靠性建模

3.1 元任务之间的关系

由图3所示的模型可知，元任务组或由几个元任务组合而成，或由元任务和元任务组组合而成，组成元任务组的各元任务或元任务组开始参与工作的时刻不同、工作时间长短不同，并连续或断续出现在各阶段任务中，各阶段转换的时机无特定规律可循，这给元任务组的可靠性建模带来了难度。

软件程序运行时，各功能的完成是由总程序不断调用各个子程序或函数来完成的，同样，数控机床加工零件的总任务可以看成是由总任务不断调用各元任务组或元任务来完成的。

卧式加工中心的加工过程中，某一时刻所有元任务或元任务组都有两个状态(执行状态和待执行状态)，则某一时刻n个元任务或元任务组共有2n个组合，因此在某一时刻总任务的状态共有2n个。加工过程实际就是各状态的不断转移过程，且各状态之间的相互转移过程是一个典型的时间连续但状态离散的随机过程，这恰好符合马尔可夫过程理论，因此我们可以采用马尔可夫方法对元任务组进行建模。

由于元任务组所处层次的不同，各元任务组之间存在包含与被包含的关系，所以我们必须从底层向顶层逐层建模，从而完成卧式加工中心总任务可靠性的建模。

我们根据最重要的时间顺序将构成高层次元任务组的各低层元任务和元任务组之间的关系分为串行、并行、并串行、串并行、循环和随机。串行关系即各元任务在时间上依次顺序执行;并行关系即各元任务或低层次元任务组在时间上同时执行;循环关系即各元任务在时间上依次循环且不断重复执行;随机关系是指某一时刻元任务组内执行的各元任务或低层次元任务组有一个或多个，且他们之间的转变没有规律，完全是随机组合。各元任务或元任务组之间的时间顺序关系不同，建立的模型也不同。

3.2 各种关系元任务组可靠性模型的建立

为了能够明确各元任务之间的转移过程，我们利用马尔可夫理论，首先建立构成元任务组的各元任务或低层次元任务组的状态转移图。我们用状态“1”表示某时刻该元任务或低层次元任务组在执行，状态“0”表示某时刻该元任务或低层次元任务组在待执行。某元任务组中存在n个元任务或低层次元任务组时，该元任务组的状态空间就是2n个，但要去掉那些在原则上不可能存在的状态空间。根据元任务组内各元任务或元任务组的执行顺序，建立元任务组状态转移图。然后，根据元任务组状态转移图建立元任务组状态转移矩阵。最后，以元任务组状态转移矩阵为基础，根据Chapman－Kolmogorov方程，建立元任务组的可靠性模型。

构成高层次元任务组的各低层元任务和元任务组之间的关系共有6种，要建立总任务的可靠性模型，就需要建立6种关系的可靠性模型，由于篇幅关系，不可能把6种关系的可靠性建模全部介绍，因此本小节只以串行关系元任务组的可靠性模型为例，介绍其建模步骤，其他的关系建模采用相同方法，在此不再一一赘述。下面详细介绍串行关系元任务组的可靠性建模过程:

(1)由串行关系元任务组的定义可知，其可靠性结构模型如图4所示。

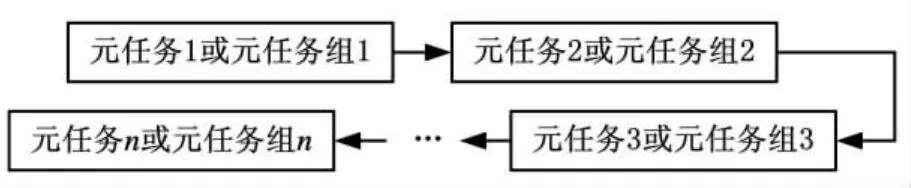
图4 串行关系元任务组可靠性结构模型图

(2)由于该元任务组有n个元任务或低层次元任务组，所以该元任务组的状态有2n个，分别从(000…0)到(111…1)。由于各元任务或低层次元任务组是串行关系，所以在某一时刻只有1个元任务或低层次元任务组在执行，因此，其状态空间只有n个，分别是(100…0)、(010…0)、(001…0)、…、(000…1)，用行阵［1 0 0 …0］、［0 1 0 … 0］、…、［1 0 0 … 1］表示它们的状态。

根据该元任务组可靠性结构模型得到其状态转移图(图5)。

图5 串行关系状态转移图

(3)根据该元任务组状态转移图得到其1步状态的转移矩阵，因为该元任务组共有n个状态，所以为n阶矩阵。由于各状态之间的转换是必然的，所以转移概率均为1。

因此，可得该元任务组的1步状态转移矩阵和n步状态转移矩阵:

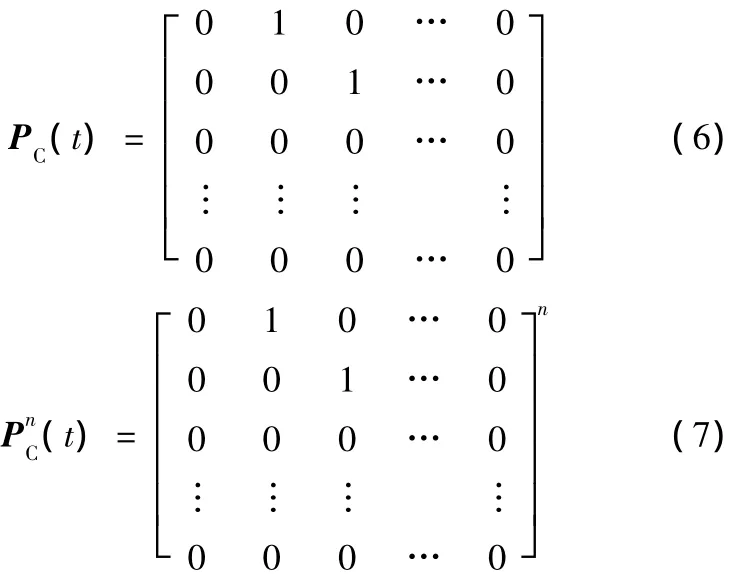
那么由初始状态I0=［1 0 0 … 0］，转移i步后，该元任务组的状态为

(4)根据Chapman－Kolmogorov方程可得该元任务组中正在执行的元任务或元任务组的可靠度:

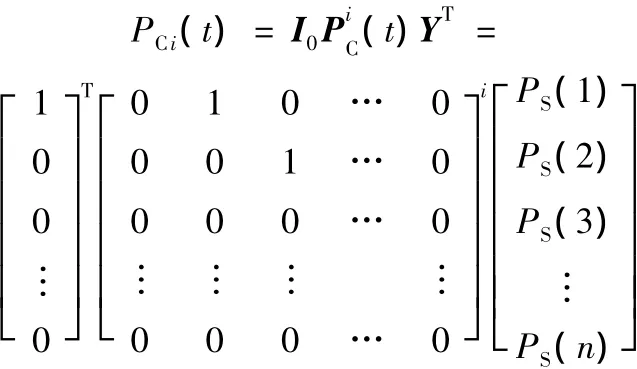
式中，YT为该元任务组内各元任务或元任务组的可靠性模型组成的列阵，YT=［PS(1)PS(2) …PS(n)］T。

由此可得，该元任务组的可靠性数学模型:

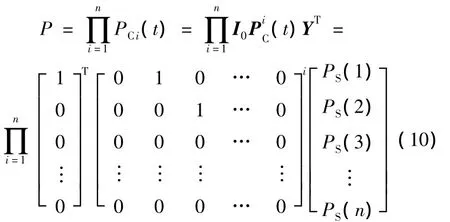
同理，可得并行、并串行、串并行、循环和随机关系元任务组的可靠性模型，在此不再罗列。

3.3 数控机床加工总任务可靠性模型的建立

我们以2.2节中建立的各元任务可靠性模型为基础，根据3.2节中各种关系元任务组可靠性建模理论，按照树形任务剖面图(图3)由底层向顶层依次建立卧式加工中心总任务可靠性模型。由于我们已经在2.2节中建立了第6层任务剖面的3个元任务的可靠性模型(式(3)～式(5))，所以我们直接从第5层开始。第5层任务剖面包括两个元任务组:托盘升降运动元任务组和托盘旋转运动元任务组。

托盘升降运动元任务组包括液压动力元任务和托盘升降运动元任务，因为托盘升降运动元任务依靠液压动力元任务驱动执行，所以它们之间是串行关系。故我们将式(3)、式(5)代入串行系统可靠性模型(式(10))，可得托盘升降运动元任务组的可靠性模型:

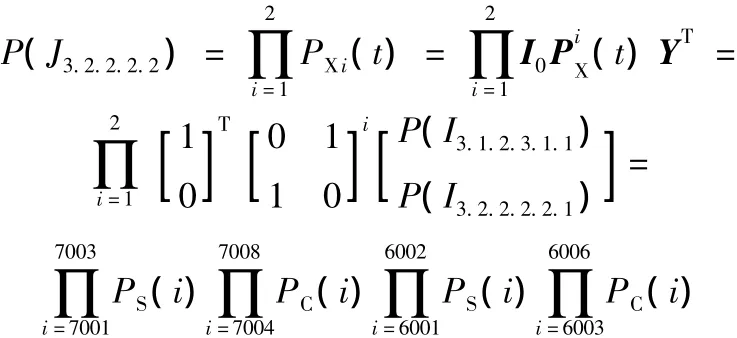
托盘旋转运动元任务组包括液压动力元任务和托盘旋转运动元任务。因为托盘旋转运动元任务依靠液压动力元任务驱动执行，所以它们之间也是串行关系。故我们将式(4)、式(5)代入串行系统可靠性模型(式(10))，可得托盘旋转运动元任务组的可靠性模型:

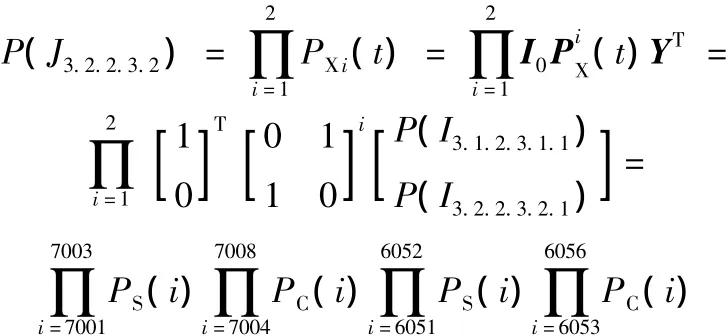
同理，我们可以从底层向顶层依次建立各层次的所有元任务组的可靠性模型。所以，卧式加工中心加工零件的总任务可靠性模型为

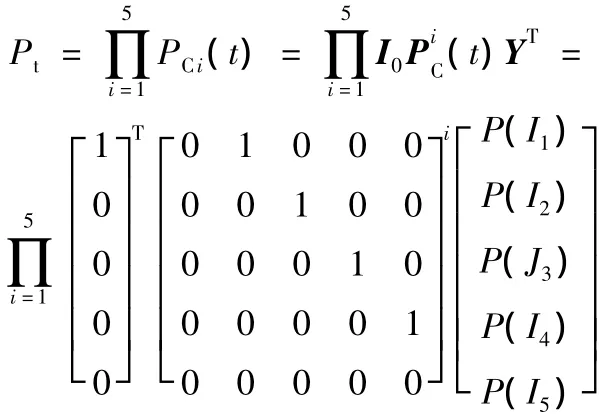
4 结语

本文在阐述数控机床加工过程复杂性特点的基础上，提出了基于任务的动态可靠性建模方法，并以某型国产加工中心为例，建立了其加工过程的可靠性模型，为数控机床可靠性建模提出了一种新的研究思路。

［1］贾亚洲，杨兆军.数控机床可靠性国内外现状与技术发展策略［J］.中国制造业信息化，2008(4):35-37.

Jia Yanzhou，Yang Zhaojun.Research Status of Reliability of NCMachine［J］.Manufacture Information Engineering of China，2008(4):35-37.

［2］贾亚洲.可靠性向国产数控装备提出挑战［J］.机电国际市场，2001(4):14-16.Jia Yanzhou.The Challenge of Reliability of CN Machine［J］.International Market of Machine，2001(4):14-16.

［3］普罗尼科夫A C.数控机床的精度与可靠性［M］.李昌琪，译.北京:机械工业出版社，1987.

［4］Vasilev V S.Cost Efficiency Approach to the Selection of NC Machine Tool Reliability Standards［J］.Soviet Engineering Research，1985，5(9):49-50.

［5］Jia Yazhou，Shen Guixiang，Jia Zhixin.A Reliability Approach to Machine Tool Bearings［J］.Reliability Engineering and System Safety，1995，50(1):127-134.

［6］Jia Yazhou，Holim W，Jia Zhixin.Probability Distribution ofMachining Center Failures［J］.Reliability Engineering and System Safety，1995，50(1):121-125.

［7］张根保，庞继红，陈国华，等.数控装备质量的模糊物元综合评价方法［J］.重庆大学学报，2011，34(1):36-41.

Zhang Genbao，Pang Jihong，Chen Guohua，et al.A Comprehensive Evaluation Method of Fuzzy Matter Element for CNC Equipment Quality［J］.Journal of Chongqing University，2011，34(1):36-41.

［8］张根保，葛红玉，刘佳，等.可靠性驱动的装配过程建模及预测方法［J］.计算机集成制造系统，2012，18(2):349-355.

Zhang Genbao，Ge Hongyu，Liu Jia，et al.Assembly Process Modeling and Prediction Method of Reliability－ driven［J］.Computer Integrated Manufacturing Systems，2012，18(2):349-355.

［9］张英芝，申桂香，薛玉霞，等.数控车床主轴模糊故障树分析［J］.吉林大学学报(工学版)，2006，36(2):65-68.

Zhang Yingzhi，Shen Guixiang，Xue Yuxia，et al.Fuzzy Fault Tree Analysis of the Principal Axis of Numerical Control Lathe［J］.Journal of Jilin University(Engineering and Technology Edition)，2006，36(2):65-68.

［10］张强，艾兴，贾亚洲.数控机床可靠性信息系统信息建模［J］.山东大学学报(工学版)，2005，35(8):14-18.

Zhang Qiang，Ai Xing，Jia Yazhou.Study on Reliability Information System Modeling of CNCMachine Tools［J］.Chinese Journal of Shandong University，2005，35(8):14-18.

［11］杨兆军，李小兵，许彬彬，等.加工中心时间动态可靠性建模［J］.机械工程学报，2012，48(1):16-21.

Yang Zhaojun，Li Xiaobing，Xu Binbin，et al.Time Dynamic Reliability Modeling of Machining Center［J］.Chinese Journal of Mechanical Engineering，2012，48(1):16-21.

［12］杨建军，胡涛，黎放.基于元任务的舰船总体任务可靠性建模方法［J］.造船技术，2009(1):12-14.

Yang Jianjun，Hu Tao，Li Fang.Reliability Modeling Method of Galley Task Based on Meta － task［J］.Marine Technology，2009(1):12-14.

［13］沈祖培，黄祥瑞.GO法原理及应用［M］.北京:清华大学出版社，2004.