单机成组调度问题的约束满足建模与求解方法

姜 锐 陈亚绒， 管在林 周宏明

1.温州大学，温州，325035

2.华中科技大学数字制造装备与技术国家重点实验室，武汉，430074

0 引言

不同类型产品或工件连续加工过程中，通常要考虑发生在机器上的换型或安装时间及成本，以及由此引起的机器、工装夹具、产品、工件的损失或损坏成本。在多品种小批量生产环境下，为减少因产品范围快速扩展而引起的大量换型或安装时间，企业普遍采用基于成组技术的混流生产方式，即将结构形状、工艺以及工装等相似的产品或工件组合为批量生产，由此产生的调度问题称为 成 组/工 件 组 调 度 （group scheduling/family scheduling，GS/FS）问题［1－2］。成组调度问题一般包括以下三项任务：①将工件/零部件分配到某个加工批；②加工批内的工件排序；③加工批在机器设备上排序。

成组混流生产的本质在于对同一机器上具有相似制造特征的不同工件成组批量生产，以减少安装时间。相似工件的成批生产能够通过减少安装时间释放机器产能，但同时也将使延后加工的工件交期受到影响，因此成组调度需要平衡满足交期与安装时间减少之间的冲突关系［3］。相较于传统调度问题，成组调度问题不仅目标更多样化，而且处理的约束也更多。作为一类复杂的组合优化问题，成组调度问题的快速求解有赖于高效的调度方法。

按照机器的数量特征可以将成组调度问题分为单机、并行机与多机等类型［4－5］，单机成组调度问题因大量的工业应用需求备受关注。Hitomi等［5］最早提出了运用分支定界法确定工件和工件组的排序；Ghosh［6］提出了运用后向动态规划算法实现工件的总加权完成时间最小化；Panwalkar等［7］提出了按照SPT与EDD规则实现单机成组调度问题总延迟时间最小化的PSK法；Liao等［8］提出了一种基于启发式算法的禁忌搜索方法求解存在主要与次要安装时间的成组调度问题；王秀利等［9］针对总流程时间最小化的单机成组作业优化调度问题，提出了基于优化性质的构造性启发算法；Mason［10］提出了一种使用SWPT（shortest weighted processing time）规则的遗传算法实现工件的加权完成时间最小化；聂黎等［11］针对最小化提前/拖期惩罚的单机调度问题，研究了运用基因表达式编程及其改进算法前序基因表达式编程的求解方法；Crauwels等［12］开发了模拟退火、禁忌搜索等多个邻域搜索启发式方法最小化工件的加权完成时间。

以上针对单机成组调度问题的研究在不同程度上为相关的后续研究提供了基础，但面对更为复杂的现实问题需要更为有效的建模方法和求解方法。本文针对单机成组调度问题工件组是否分批、安装时间与工件排序是否有关等复杂的约束特征，将其作为一类约束满足问题，构建了更接近于现实问题表达的单机成组调度约束模型，以最小化加权流程时间与加权拖期为目标，设计了启发式搜索与约束传播相结合的求解方法，实现了不同类型问题的快速建模和求解。

1 单机成组调度问题描述

起源于人工智能领域的约束满足技术通过分离问题的建模与求解算法，以更加接近于现实世界的方式描述问题及其复杂的约束，利用变量之间的约束关系传播与一致性检验等方法进行模型求解，在有效解决复杂问题，特别是在组合优化问题方面具有非常明显的优势。此外，约束满足方法还允许用户在不改变算法的情况下，通过增减约束动态地修改模型，为其他问题所重用，因此利用约束满足方法进行生产调度问题建模和求解得到了广泛的关注和研究。目前的约束满足计划调度问题研究主要限于传统的车间作业调度，如Beck等［13］提出了基于资源依赖度和争用度等动态问题结构信息的启发式搜索技术求解车间调度问题，Watson等［14］研究了混合约束规划与局部搜索方法求解车间调度问题。在运用约束满足的方法解决成组调度问题方面，尽管 Malapert等［15］提出了研究对象为批处理时间下的成批以及排序问题，但迄今文献中尚未出现运用约束满足方法的工件可用性条件下的单机成组调度问题研究。

单机成组调度是指将多个属于不同工件组的工件加工任务根据相似性分派到制造资源的过程，如图1所示，其目的是综合考虑制造资源能力、工件成组特性、工件交期等约束，合理安排工件批和工件的生产活动以同时满足约束和优化目标。因此，单机成组调度问题是一类有限域约束满足问题或约束优化问题（COPs），且大多数都是NP难题。

图1 机器M1的成组生产示意图

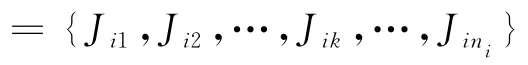
对于成组调度问题，一般假设：每一种工件组的加工都需要精确的安装时间，而且此安装时间远远大于工件的加工时间，该假设被称为成组假设。如果成组假设成立，则同一工件组内的工件在机器上连续加工，每一工件组的处理时间等于该工件组中所有工件的处理时间总和；否则，同一工件组内的工件可分割加工。通常将连续加工的一系列工件集合称为一个加工批，如果加工批中的所有工件加工完成之后通过托盘、箱子或拖车等容器运输到下一工序进行加工，则称为批可用性；否则称为工件可用性。本文的研究对象为工件可用性条件下的单机成组调度问题。

表1 成组调度问题的参数变量与值域

图2 工件组安装时间独立于工件组排序且不可分割加工调度示意图

图3 工件组调度方案中的运行含义

图4 工件组安装时间独立于工件组排序且可分割加工调度示意图

对于单机成组调度问题，如果工件组i或运行r（下文统称为工件组）的安装时间与之前处理的工件组无关，则认为工件组的安装时间独立于工件组排序；如果安装时间依赖于之前处理的工件组，则认为工件组的安装时间依赖于工件组排序（sequence－dependent setup times，SDST）。

根据工件可用性条件下的单机成组调度问题的加工特征，可将其分为4种子问题：①工件组安装时间独立于工件组排序且不可分割加工问题；②工件组安装时间独立于工件组排序可分割加工问题；③工件组安装时间依赖工件组排序不可分割加工问题；④工件组安装时间依赖工件组排序可分割加工问题。

2 问题的约束满足模型

2.1 单机成组调度问题的决策变量

成组调度问题旨在为每一个工件组及工件安排一个合理的制造期间，保证优化目标实现。影响成组调度目标实现的决策变量主要是序变量，包括工件组排序与工件组内工件排序，O（i）表示排在第i位置的工件组序号，O（i）∈ ｛1，2，…，f｝；O（i，k）表示排在工件组i中第k位置的工件序号，O（i，k）∈ ｛1，2，…，ni｝。

根据决策变量，事先给定的参数变量值将更新，如工件组JO（i）的开始加工时间为st O（i），工件JO（i，k）的开始加工时间为st O（i，k），工件组JO（i）的加工时间为p O（i），工件JO（i，k）的加工时间为p O（i，k），其他依此类推。为了用决策变量描述工件组之间的安装时间，假设用F＝｛1，2，…，f｝表示工件组集合，引入虚拟工件组0，生成F0＝ ｛0，1，…，f｝。对工件组排序，得到序变量集合OF＝ ｛O（0），O（1），…，O（f）｝，则排在第i位置的工件组的安装时间为s O（i－1）O（i），如果工件组的安装时间与排序无关，则为sO（i）。对于增加的虚拟工件组0，有O（0）＝0，p0＝0，d0＝0，w0＝0。

2.2 单机成组调度问题的约束

对于以上给出的4种单机成组调度问题，运用约束满足方法建模，主要包括如下约束。

（1）工件成组特性约束。

①工件j只能属于一个工件组i，即

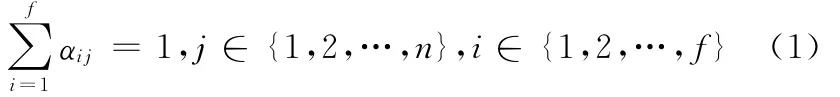
②属于工件组i的工件数量总和为n i，即

③所有工件组的工件数量ni之和为总工件数量n，即

④所有运行r的工件数量βr之和为总工件数量n，即

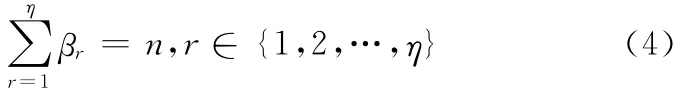
⑤工件组i或运行r的权重为

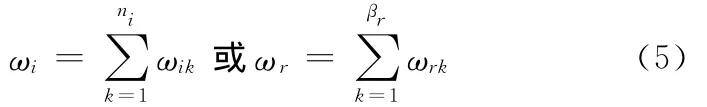
（2）工件组的处理时间约束。

①工件组不可分割加工，将工件组i整体作为一个复合工件，其处理时间为

②工件组可分割加工，用βr表示分割之后运行r中的工件数量，则运行r的处理时间为

（3）工件组的加工时间满足以下析取约束：

（4）工件的加工时间约束。

① 工件JO（i，ni）与工件JO（i＋1，1）的加工时间满足以下析取约束：

② 工件JO（i，k）与工件JO（i，k＋1）满足以下条件：

（5）工件JO（i，k）的完成时间约束。

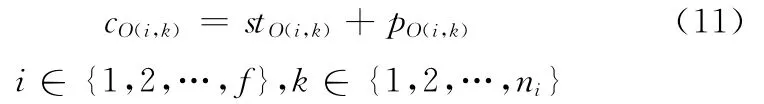
（6）工件JO（i，k）的拖期约束。

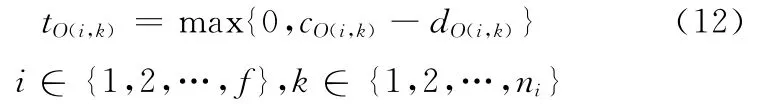
2.3 单机成组调度问题的目标

成组调度通过将相似工件成组加工以减少安装时间，可能会导致工件拖期。在精益生产方式盛行的今天，准时是企业获得市场竞争的关键要素，对于多品种小批量生产，在进行批量成组生产时，既要节约安装时间，也要保证产品交期。因此，本文以最小化加权流程时间与加权拖期为目标，即

3 基于约束满足的问题求解方法

针对成组调度问题的多目标优化，目前文献中一般通过为各个目标设置权重等方法将多目标优化转化为单目标优化，具有一定的主观性，且求解的复杂性高。因此，本文将最小化加权流程时间与加权拖期目标的优化分为两个阶段完成。第一阶段，以最小化加权流程时间为目标，对工件组进行排序或将工件组分割成运行，确定运行的排序；第二阶段，以确定的排序作为初始解，其对应的加权流程时间作为约束，优化工件组或运行排序，最小化加权拖期。算法主流程如图5所示，图中①～④分别对应单机成组调度问题的4种子问题。

3.1 工件组分割条件

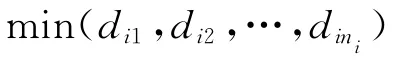
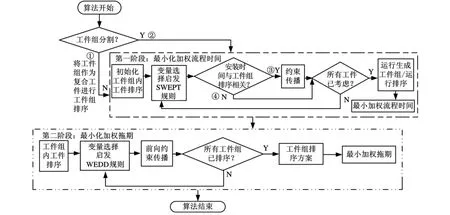
图5 单机成组调度问题的算法流程

3.2 最小化加权流程时间的变量排序启发式搜索算法

（1）工作组内工件排序初始化。对于工件组Ji中的工件J ik按照SWPT规则排序，如果此值相同，按照加权最早交期（weighted earliest duedate，WEDD）规则排序，得到工件组Ji的排序集合

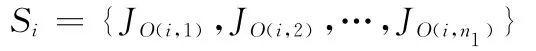
令β＝ ∅，η＝1，进入步骤（2）。

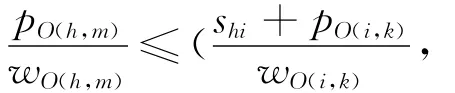
对于成组调度，组内工件的排序运用WEDD规则是可行的，但是工件组中任意一个工件都可能产生最大拖期，因此需要对工件组的交期进行调整。假设工件组i内的工件已经按照WEDD规则排序，且工件组从st O（i）开始加工，则工件组i中k位置的工件J O（i，k）的拖期时间为

式（13）中，qO（i，k）＝p i－ （p O（i，1）＋p O（i，2）＋ …＋p O（i，k）），表示工件JO（i，k）完成之后的工件组剩余处理时间。如果定 义工件JO（i，k）的工件组调整交期d′O（i，k）＝d O（i，k）＋q O（i，k），则工件组中工件的最大拖 期 是 maxk（cO（i，k）－d O（i，k））＝st O（i）＋p O（i） －mink（d′O（i，k））。因此，定义 工 件 组的交 期d O（i）＝mink（d′O（i，k））。一旦工件组中工件按照 WEDD 规则排序，此值很容易确定，且不依赖于工件组的开始处理时间。

3.3 最小化加权拖期的变量排序启发式搜索与前向约束传播混合方法

以第一阶段获得排序S为初始可行解，按照“如果对于所有工件组i，g，q，安装时间满足siq≤sig＋sgq，即三角不等式，则最优解中工件组的排序依然满足交期按照非降顺序排列［2］”规则，设计了以工件组排序变量启发式搜索与前向约束传播混合的算法（与3.2节类似，这里给出的算法适用于安装时间依赖工件组排序的问题）。

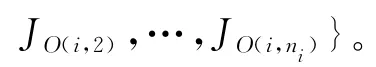
图6 工件组排序规则

表2 深度优先搜索域缩减规则

（4）按照已经排序的工件组变量生成调度方案。

5 实例验证

运用以上建模与求解方法对某企业的成组生产调度问题进行了实例验证。该企业针对多品种小批量需求，采用成组生产组织形式，某生产期间有工件加工任务14项，各项任务的处理时间、交货时间、权重以及成组信息如表3所示。

表3 车间工件生产任务信息

机器上的安装时间分为两种，一种是安装时间，一种是依赖于工件组排序的安装时间，具体数据如表4所示。其中第一行和第一列中工作组f1～f5分别表示安装时间的计算起点和终点。

表4 机器上工件组的安装时间 min

4.1 工件组不可分割加工结果

对于表3所示的14项工件任务，当工件组不可分割加工时，则在排序时将工件组整体作为一个复合工件，按照前面提出的方法，计算各个复合工件的加工时间、权重和调整交期，结果如表5所示。

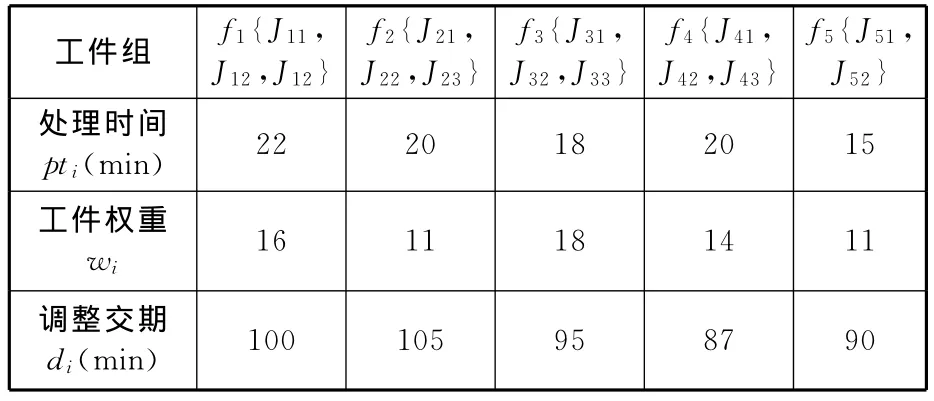
表5 工件组不可分割加工数据表

运用本文提出的方法进行求解，分别得到工件组安装时间与排序有关、工件组安装时间与排序无关两种情况下的结果，两种结果的比较如表6所示。

表6 工件组不可分割加工情况下的两种运算结果比较

由表6可以看出，安装时间与工件组排序无关、安装时间与工件组排序有关两种情况下的最优排序方案不同，安装时间、目标值也存在较大差异。在安装时间与工件组排序有关情况下，通过合理安排工件组的先后顺序，调整了工件组f4与工件组f3的顺序，将安装时间从75min缩减为45min，从而缩减了工件组的加权流程时间。

4.2 工件组可以分割加工结果

当工件组可以分割加工时，需要通过以SWPT为准则的工件组内排序变量赋值，SWEPT为准则的工件组排序变量赋值，首先对工件组进行分割。运行算法发现，当工件组安装时间与排序无关时，工件组未进行分割，结果与工件组不可分割加工情况下相同。分析产生这种结果的原因在于工件组安装时间为固定值，且大于等于工件的加工时间，也就是符合前面提出的成组假设，在这种情况下，工件组通常是不分割加工的。

当工件组的安装时间依赖工件组排序时，对5个工件组进行分割，得到7个运行，R＝｛r1，r2，r3，r4，r5，r6，r7｝＝ ｛（J11，J13，J12），（J51），（J31，J33，J32）， （J21，J23）， （J52）， （J42，J41，J43），（J22）｝。对这7个运行进行排序，得到最优的排序方案为：S＝ ｛（J42，J41，J43），（J31，J33，J32），（J11，J13，J12），（J51），（J52），（J21，J23），（J22）｝。对应的加权流程时间为4693min，加权拖期为1002min，目标值为5695min。可以看出，在最优排序方案中，属于同一工件组的运行r2＝｛J51｝和运行r5＝ ｛J52｝，运行r4＝ ｛J21，J23｝和运行r7＝ ｛J22｝，由于安装时间的缘故，按照先后紧接的顺序生产。

5 结语

本文针对单机成组调度问题，首先根据工件可用性条件下安装时间是否与工件排序相关、工件组能否分割加工等加工特征，对单机成组调度问题进行了类型分析；其次，考虑工件成组特性、工件组交期、处理时间等多种制约条件，借鉴约束满足的理论和方法，以工件组和工件的排序变量为决策变量，构建了约束满足模型；再次，采用两阶段优化方法，设计了以问题结构和优化特征为指导的启发式搜索与约束传播混合的求解方法；最后，运用提出的建模和求解方法对某企业的成组生产调度问题进行了实例验证。本文提出的方法允许通过添加或改变少量约束方便地改变问题模型，在不改变算法的情况下动态地修改模型，快速地解决单机成组调度问题的4种子问题。

［1］Potts C N.Scheduling Two Job Classes on a Single Machine［J］.Computers ＆ Operations Research，1991，18（5）：411－415.

［2］Webster S，Baker K R.Scheduling Groups of Jobs on a Single Machine［J］.Operations Research，1995，43（4）：692－703.

［3］陈亚绒，管在林，彭运芳，等.面向大规模定制的瓶颈成组调度启发式方法研究［J］.中国机械工程，2010，21（8）：957－962.

Chen Yarong，Guan Zailin，Peng Yunfang.Research on Bottleneck Group Scheduling Heuristics for Mass Customization［J］.China Mechanical Engineering，2010，21（8）：957－962.

［4］Potts C N，Kovalyov M Y.Scheduling with Batching：A Review［J］.European Journal of Operational Research，2000，120（2）：228－249.

［5］Hitomi K，Ham I.Operations Scheduling for Group Technology Applications［J］.Annals of the CIRP，1976，25（1）：419－422.

［6］Ghosh J B.Batch Scheduling to Minimize Total Completion Time［J］.Operations Research Letters，1994，6（5）：271－275.

［7］Panwalkar S S，Smith M L，Koulamas C P.A Heuristic for the Single Machine Tardiness Problem［J］.European Journal of Operational Research，1993，70（3）：304－310.

［8］Liao L M，Liao C J.A Tabu Search Approach for Single Machine Scheduling with Major and Minor Setups［J］.International Journal of Industrial Engineering：Theory Applications and Practice，2002，9（2）：174－183.

［9］王秀利，吴惕华，刘磊.一种求解单机成组作业优化调度的启发算法［J］.计算机仿真，2003，20（2）：48－50.

Wang Xiuli，Wu Xihua，Liu Lei.A Heuristic Algorithm for Single Machine Scheduling with Job Class Setups［J］.Computer Simulation，2003，20（2）：48－50.

［10］Mason A J.Genetic Algorithms and Scheduling Problems［D］.Cambridge：University of Cambridge，UK，1992.

［11］聂黎，高亮，胡译丹.基于前序基因表达式编程的单机成组调度算法［J］.计算机集成制造系统，2008，13（11）：2261－2268，2275.

Nie Li，Gao Liang，Hu Yidan.Prefix－gene－expression－programming－based Algorithm for Scheduling Groups of Jobs on a Single Machine［J］.Computer Integrated Manufacturing Systems，2008，13（11）：2261－2268，2275.

［12］Crauwels H A J，Potts C N，van Wassenhove L N.Local Search Heuristics for Single Machine Scheduling with Batch Set－up Times to Minimize Total Weighted Completion Time［J］.Annals of Operations Research，1997，70：261－279.

［13］Beck J C，Fox M S.Dynamic Problem Structure A－nalysis as a Basis for Constraint－directed Scheduling Heuristics［J］.Artificial Intelligence，2000（117）：31－81.

［14］Watson J P，Beck J C.A Hybrid Constraint Programming/Local Search Approach to the Job－Shop Scheduling Problem［C］//Conference on Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems.Paris，2008，5015：263－277.

［15］Malapert A，Guéret C，Rousseau LM.A Constraint Programming Approach for a Batch Processing Problem with Non－identical Job Sizes［J］.European Journal of Operational Research，2012，221（3）：533－545.