井间示踪测试组合解释方法研究

刘同敬，第五鹏祥，姜宝益，刘 睿，孙 利，8

（1.中国石油大学 （北京）提高采收率研究院，北京 102249；2.中石油三次采油重点实验室，北京 102249；3.北京市温室气体封存与资源化利用重点实验室，北京 102249；4.中国石油大学 （北京）石油工程教育部重点实验室，北京 102249；5.中国地质大学 （北京）能源学院，北京 100083；6.中国华电集团科学技术研究总院，北京 100035；7.中国石油大学 （北京），北京 102249；8.中国产业安全研究中心，北京 100044）

在建立的数学模型、求解方法的基础上，确定了自变量，建立了目标函数，利用改进的遗传算法，完成示踪测试曲线的拟合和油藏参数解释，形成了井间水相示踪测试解释流程［1－3］。由于井间示踪测试解释涉及的参数较多，过程较为复杂，因此，参数解释过程利用最优化方法完成。

1 目标函数建立

首先，根据研究的问题确定了参数自变量。对于井间示踪测试解释，通过区块所有曲线同时拟合直接得到的主要参数如下所示［4－8］。

1）不同井组示踪剂产出通道的分布情况。人为设定高渗通道数目上限的情况下，由算法通过曲线拟合，确定具体的高渗通道数目及其垂向分布情况。

2）不同井组平面流线上示踪剂突破的情况。平面流线的突破条数对浓度曲线的上升、下降情况影响大。

3）不同井组各个高渗通道不同流线上的厚度。高渗通道的厚度对产出浓度的峰值影响较大，同时会影响产出时间以及浓度曲线分布情况。

4）不同井组各个高渗通道不同流线上的渗透率。高渗通道的渗透率对见剂时间影响较大，同时会影响到产出浓度峰值和浓度曲线分布情况。

5）双示踪剂测试时，确定高渗通道剩余油饱和度的分布。

由于地下情况复杂、自变量较多，并且示踪剂产出曲线拟合过程中人为调整的难度大，因此，构造目标函数，利用最优化方法完成。

确定目标函数式（1）。

式中，i为产出井编号；j为井组编号。

即利用区块所有产出井计算浓度与实测浓度的差的平方和作为目标函数，按照一定的优化方法，当目标函数最小时，得到的地层参数即认为是最可能的参数分布。

2 大规模系统优化的遗传算法

由于求解的问题自变量很多，以研究范围内有两个测试井组，每个测试井组有2口示踪剂产出井，每口产出井垂向有2个高渗通道，每对井间有20条流线连接，每条流线上有2个参数计算，则有很多个参数可以调整，是典型的大规模参数系统。

虽然借助油藏工程分析判断手段，可以消除或者确定部分参数，但是，需要拟合的自变量依然很多，常规的最优化方法已经证实适用性差，因此，最终筛选确定了利用组合最优化方法之一－遗传算法进行改进，作为拟合的工具。

2.1 遗传算法的实现原理

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法。随着问题种类的不同，以及问题规模的扩大，要寻求到一种能以有限的代价来解决一些优化问题的通用方法仍是一个难题。遗传算法却为解决这类问题提供了一个有效途径和通用框架［9－10］。

遗传算法中，将n维决策向量X＝［x1，x2，…，xn］T用n个记号Xi（i＝1，2，…，n）所组成的符号串表示，见公式（2）。

把每个Xi看作一个遗传基因，它所有可能的取值称为等位基因，这样，X就看做是由n个遗传基因组成的一个染色体。根据研究的问题，这里的等位基因是某一范围内的实数值。这种编码所形成的排列形式X是个体的基因型，与它相对应的X值是个体的表现型。染色体X也称为个体X，对于每一个个体X，要按照一定的规则确定出其适应度。个体的适应度与其对应的个体表现型X的目标函数值相关联，X越接近于目标函数的最优点，其适应度越大。

遗传算法中，决策变量X组成了问题的解空间。对问题最优解的搜索是通过对染色体X的搜索过程来实现的，从而由所有的染色体X就组成了问题的搜索空间。

生物的进化是以集团为主体的。与此相对应，遗传算法的运算对象是由M个个体所组成的集合，称为群体。与生物的进化过程相类似，遗传算法的运算过程也是一个反复迭代的过程，第t代群体记为P（t），经过一代遗传和进化后，得到第t＋1代群体，记为P（t＋1）。这个群体不断地经过遗传和进化操作，并且每次都按照优胜劣汰的规则将适应度较高的个体更多地遗传到下一代，这样最终在群体中将会得到一个优良的个体X，它所对应的表现型X将达到或接近于问题的最优解。

生物进化的过程主要是通过染色体之间的交叉和染色体的变异来完成的。与此相对应，遗传算法中最优解的搜索过程也模仿生物的进化过程，使用所谓的遗传算子作用于群体P（t），进行下述遗传操作，从而得到新一代群体P（t＋1）。

1）选择：根据各个个体的适应度，按照一定的规则或方法，从第t代群体P（t）中选择出一些优良的个体遗传到下一代群体P（t＋1）中。

2）交叉：将群体P（t）内的各个个体随机或者按照一定规则搭配成对，对每一对个体，以某个概率（交叉概率）交换他们之间的部分染色体。

3）变异：对群体P（t）中的每一个个体，以某一概率（变异概率）改变某一个或某一些基因座上的基因值为其它的等位基因。

基于上述三种遗传算子的遗传算法的主要运算流程如下所示。

步骤一：初始化。设置进化代数计数器t＝0，设置最大进化代数T，随机生成M个个体作为初始群体P（0）。

步骤二：个体评价。计算群体P（t）中各个个体的适应度。

步骤三：选择运算。将选择算子作用于群体。

步骤四：交叉运算。将交叉算子作用于群体。

步骤五：变异运算。将变异算子作用于群体。群体P（t）经过选择、交叉、变异运算之后得到下一代群体P（t＋1）。

步骤六：终止条件判断。若t＜T，则转到步骤二；若t≥T，则以进化过程中所得到的具有最大适应度的个体作为最优解输出，终止计算。

运算过程见图1。

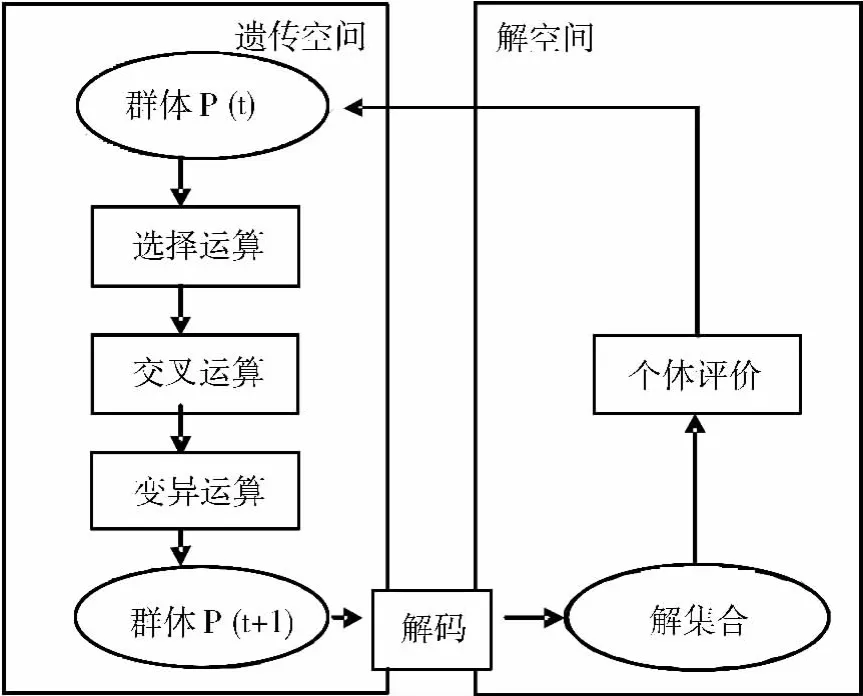
图1 遗传算法过程

遗传算法与直接法、梯度法等的不同在于其有多个随机产生初始点，搜索过程随机，且有自己的交叉、变异和选择遗传操作。对于复杂的优化问题，遗传算法具有优势。

2.2 改进的浮点数编码遗传算法

在遗传算法中如何描述问题的可行解，即把一个问题的可行解从其解空间转换到遗传算法所能处理的搜索空间的转换方法就称为编码。常用的编码方法有二进制编码法、格雷码编码法、浮点数编码法、符号编码法、多参数级联编码法和多参数交叉编码法等。浮点数编码方法是指个体的每个基因值用其某一范围内的一个浮点数来表示，个体的编码长度等于其决策变量的个数。因为这种方法使用的是决策变量的真实值，所以浮点数编码方法也叫做真值编码法。下面介绍基于浮点数编码的遗传算法实现过程。

2.2.1 初始化过程

随机产生M个初始染色体。由于优化问题的复杂性，解析地产生可行的染色体是困难的。此时，采用下述方法作为初始化过程：①通过油藏工程分析，确定一个包含最优解的区域，即一个n维超立方体；②从这个超立方体中产生一个随机点，并检验其可行性，如果可行，则作为一个染色体，否则，从超立方体中重新产生随机点，直到得到可行解为止；③重复以上过程M次，得到初始可行的染色体组合。

2.2.2 评价函数

评价函数用来对种群中的每个染色体设定一个概率，以使该染色体被选中的可能性与其适应性成正比，在此，直接利用目标函数倒数的相对大小作为评价函数，不采用其它通用性的评价函数

2.2.3 选择过程

由于要解决的问题具有一定优化方向，因此，不采用通用旋转赌轮的方法进行选择，而是直接根据评价函数进行排序，从好到差选择M1个个体进入下面的优化程序。

2.2.4 交叉过程

由于要解决的问题中，评价函数仅从目标函数的角度对个体进行了评价，不能够完全反映实际优化的程度，因此，交叉过程中，不再继续依赖评价函数，而是采用完全随机的操作方法。

1）生成两个随机数，从M1个个体中确定两个个体X1和X2。

2） 生成一个随机数c，利用选出的两个个体，交叉操作，形成两个新的后代个体

3）重复以上过程M2次，得到交叉形成的个体组合M2个，在该问题中，要求M2大于M1。

2.2.5 变异操作

根据研究的问题特征，认为变异操作在本组合优化中所占比例很大，因此，确定变异操作产生的个体数量M3大于M2与M1之和，且该变异为完全变异，即可以随机产生个体作为变异个体，其产生方法与初始化过程相同。

2.2.6 个体数量

通过选择、较差、变异得到的个体进入下一个循环，且要求M＝M1＋M2＋M3。可见，改进的遗传算法特点主要包括：①从油藏工程评价的角度，简化了评价函数，直接用目标函数简单处理作为评价函数，节省了不必要的计算，操作过程中，较为合理的处理了随机和方向的关系，具有针对性；②在保留适应个体的前提下，着重强调了变异的作用，从数量上，变异个体数量大，从变异程度上，属于完全变异，适应了多参数、范围大的情况；③交叉操作在此实质上相当于一种变异作用的补充和较优个体主要特征的继承，不再依赖于评价函数，是一种有优化方向的交叉操作。

2.3 组合优化控制算法实现过程

根据组合优化解释的数学模型和示踪剂产出浓度方程可知，目标函数中的自变量均具有一定的变化范围，满足一定的上下限约束。但是，依然存在自变量过多，优化困难的问题，因此，需要在改进的遗传算法基础上，根据研究的问题，进一步构造优化控制算法。

1）首先，从油藏工程和拟合实践的角度，确定了参数的敏感性排序。最为敏感的参数为井间高渗通道垂向位置、主流线上高渗通道的厚度、渗透率；其次为其它流线上的厚度、渗透率；最后为剩余油饱和度分布。

2）在敏感性排序的基础上，采用空间和参数控制的轮换优化方法。①空间控制的轮换优化方法：即一次优化一个井组，依次进行；②参数控制的轮换优化方法：即首先优化最敏感的参数，然后优化次敏感的参数，最后优化不敏感的参数，一轮优化完毕后，重复参数控制的优化过程；③每一次优化均调用改进的遗传算法优化过程，优化完毕后，修改关联参数，循环①－②直至优化结果收敛。拟合实践证明，这种控制非常有效。

3 结论

在建立的数学模型、求解方法的基础上，确定了油藏自变量，建立了目标函数，改进了遗传算法，完成示踪测试曲线的组合自动优化解释，形成了井间水相示踪测试解释流程。

［1］姜汉桥，刘同敬.示踪剂测试解释原理与矿场实践［M］.东营：石油大学出版社，2001.

［2］李淑霞，陈月明，冯其红，等.利用井间示踪剂确定剩余油饱和度的方法［J］.石油勘探与开发，2001，28（2）：73-75.

［3］姜瑞忠，姜汉桥，杨双虎.多种示踪剂井间分析技术［J］.石油学报，1996，17（3）：85-91.

［4］常学军，郝建明，郑家朋，等.平面非均质边水驱油藏来水方向诊断和调整［J］.石油学报，2004，25（4）：58-61.

［5］陈月明，姜汉桥，李淑霞.井间示踪剂监测技术在油藏非均质性描述中的应用［J］.石油大学学报：自然科学版，1994，18（zk）：1-7.

［6］Yuen，.D.L.，Brigham，W.E.and Cindo-Ley，H.Analysis of Five-Spot Tracer Test to Determine Reservoir Layering .DOE Report SAW 12658.Feb.1979.

［7］Maghsood Abbasazadeh-Dehaghani and William E.Brigham：Analysis of Well Tracer Flow to Determine Reservoir Layering.JPT.Oct.1984.

［8］Allison，S.B.，Pope，G.A.and Sepehrnoori，K.Analysis of Field Tracer for Reservoir Description.J.of Petroleum Science and Engineering.1991，5（2）：173-186.

［9］Akhil Datta Gupta，L.W.Laka and G.A.Pope and M.J.King.Type-Curve Approach to Analyzing Two-Well Tracer Tests.SPE/DOE 24139.

［10］S.G.Ghori，J.P.Heller.Use of Well-Well Tracer Tests to Determine Geostatistical Parameters of Permeability.SPE/DOE 24138.