基于分布式计算技术的导航卫星钟差预报研究

王宇谱，吕志平，陈正生，崔 阳

（信息工程大学 地理空间信息学院，郑州 450052）

1 引言

卫星钟差预报是卫星导航系统中一项非常重要的工作：1）研究钟差预报有利于提高钟差参数预报的可靠性和准确性，优化卫星钟改正数据上传时间间隔［1］；2）在实时精密单点定位中需要采用钟差预报结果参与计算来实现高精度定位［2］；3）在地面监测站观测不到导航卫星运行的弧段内，为了保持卫星钟与系统时间的同步需要根据星钟运行性能建立准确的卫星钟预报模型［3］；4）卫星自主导需要地面预报一段时间的钟差作为其先验信息［4］。因此，研究如何提高卫星钟差预报的精度和稳定性对于卫星导航系统来说相当重要。

然而，星载原子钟的钟差预报一直是时频领域中的一个难题；对此近些来年国内外学者对其进行了大量的研究［5-9］。将目前已建立的常用钟差预报模型总结起来主要包括：二次多项式 （quadratic polynomial，QP）模型、灰色模型 （grey model，GM （1，1））、卡尔曼滤波 （Kalman filter，KF）模型和谱分析模型以及自回归模型，简称这些模型中任意一种为单一模型。这些单一模型在钟差预报中各有特点和适用范围。但是由于原子钟自身的复杂变化特性、极易受外界环境的影响，在钟差预报的实际应用中用任何一种单一模型都是不完善的。因此，本文结合组合预报钟差的思想使用在信息领域广受关注的分布式计算技术，提出了一种卫星钟差的分布式预报方法，给出了该方法的详细思路和关键技术，同时分析了该技术的可行性。

2 卫星钟差的分布式预报技术体系

星载原子钟频率总波动是白噪声调相、白噪声调频和闪变噪声调相、闪变噪声调频及随机游走调频5种噪声线性叠加的结果［10］；这使建立精准的星钟运行模型变得非常困难，也导致高精度的钟差预报变得困难。在钟差预报的实际应用中使用任何一种单一模型都是不完善的，原因之一就是原子钟自身的复杂变化特性、极易受外界环境的影响。针对单一模型的不足，文献 ［11］提出了能够综合各单一预报模型特性的组合预报钟差思想，并且研究了基于修正线性组合模型的原子钟钟差预报算法和线性加权组合卡尔曼滤波在钟差预报中的应用，取得了较好的预报效果，证明了组合预报钟差思想的优势和非常好的应用前景。

然而，目前对组合预报钟差思想的研究只是初步性的，并且主要集中在线性组合模型方面，更重要的是已有的研究还存在两处明显的不足：一是由于要综合多种单一模型预报的结果，使得组合模型预报的实时性变差，特别是当所需预报的时间较长或者当用于建模的钟差数据较多时；二是目前的组合仅是对少数单一模型的初步组合，没能充分综合利用多种单一模型的优点。同时对于非线性组合方法，由于算法的复杂性和该法存在着劣组合的可能性，相关的研究非常少。所以，对于非线性组合预报问题的研究还要在深度和广度上进一步加深；在掌握非线性问题原理的基础上，使用非线性组合方法来提高钟差预报的效果。

2.1 钟差预报的分布式线性组合方法

线性组合模型是指对不同模型预报结果给以适当的权，取加权平均值来得到组合预报结果。为了克服已有线性组合预报模型的不足，使用分布式计算技术对其完善和进一步扩展。所谓分布式计算就是在两个或多个软件之间互相共享信息。这些软件既可以在同一台计算机上运行，也可以在通过网络互联起来的多台计算机之间运行［12］。组合模型是各单一模型的综合，这使得该模型本身就具有天然的分布式特性，因此使用分布式计算技术来组合更多的单一模型使组合预报模型既能获得更高精度和更高稳定性的预报结果，同时又能保证很好的时效性。

图1给出了钟差的分布式线性组合预报模型结构图，其中向量X0、T0为已知的钟差数据及其对应的时刻，T为所需预报的钟差对应的时刻组成的向量；各单一预报模型分别处在并行的子计算上，这些子计算可以是同一台计算机上多个并行的线程，也可以是计算机多核处理器的子核，还可以是多台互联的计算机，其具体类型的确定要根据所要处理的钟差数据量的多少来决定。

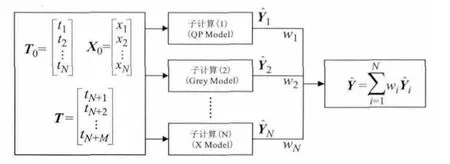
图1 钟差的分布式线性组合预报模型结构

该模型在进行钟差预报时，控制端发送运行的命令到各子计算节点，各子计算读取已知数据进行建模然后得到钟差预报结果（i＝1，…，N）；接着各子计算将结果返回给控制端，并删除数据释放存储资源。控制端在接收完返回结果后，取适当的权值进行加权求和即可求得最终的钟差预报结果。分布式线性组合预报模型的通信过程如图2所示，其中控制端通过异步多线程编程技术与各节点交互实现并行处理。系统中的所有参数预先设定，处理自动化完成；整个过程是一个计算和通信的过程，通信传输的只是简单的指令；密集的计算都分配到了各个节点，属于典型的粗粒度并行计算。对于该模型而言，其关键的技术难点是多种单一模型组合时最佳组合权的确定。

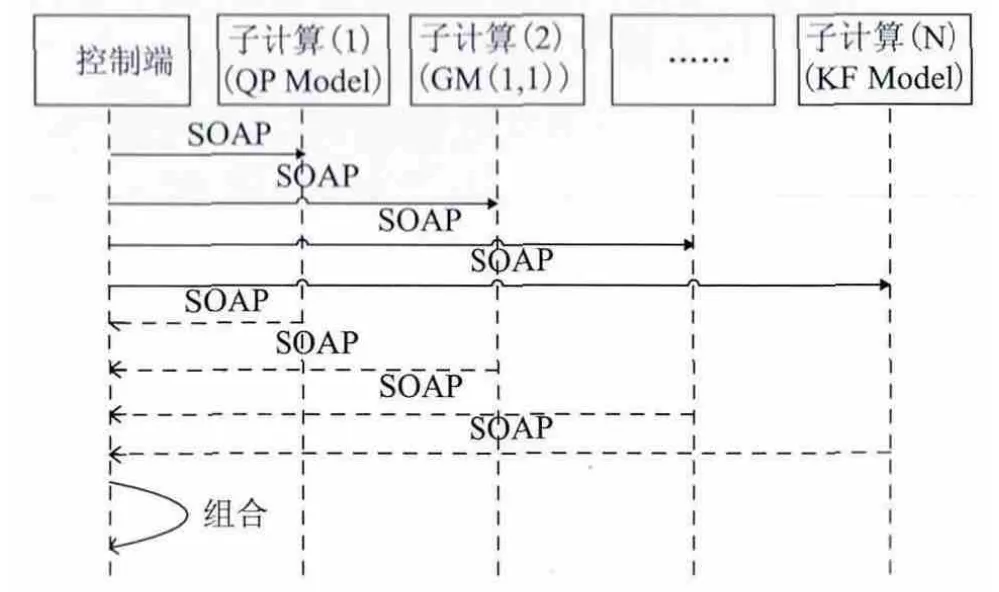
图2 分布式线性组合预报模型通信序列图

2.2 钟差预报的分布式神经网络模型

研究表明，人工神经网络能够通过对样本的学习以足够高的精度估计任何非线性的时间序列［13］；这对于像钟差这种难以得到严密数学表达式的预报问题非常合适的，特别是希望得到一种简明的预报形式。分布式神经网络模型是由多个相对独立、相互连接、协同作用的子神经网络组成的系统，是一种新型神经网络系统；这种将多个神经网络子模型通过一定方式的连接后，在对象整个输入空间内模型的预测精确度和鲁棒性都将会得到增强［14-15］。

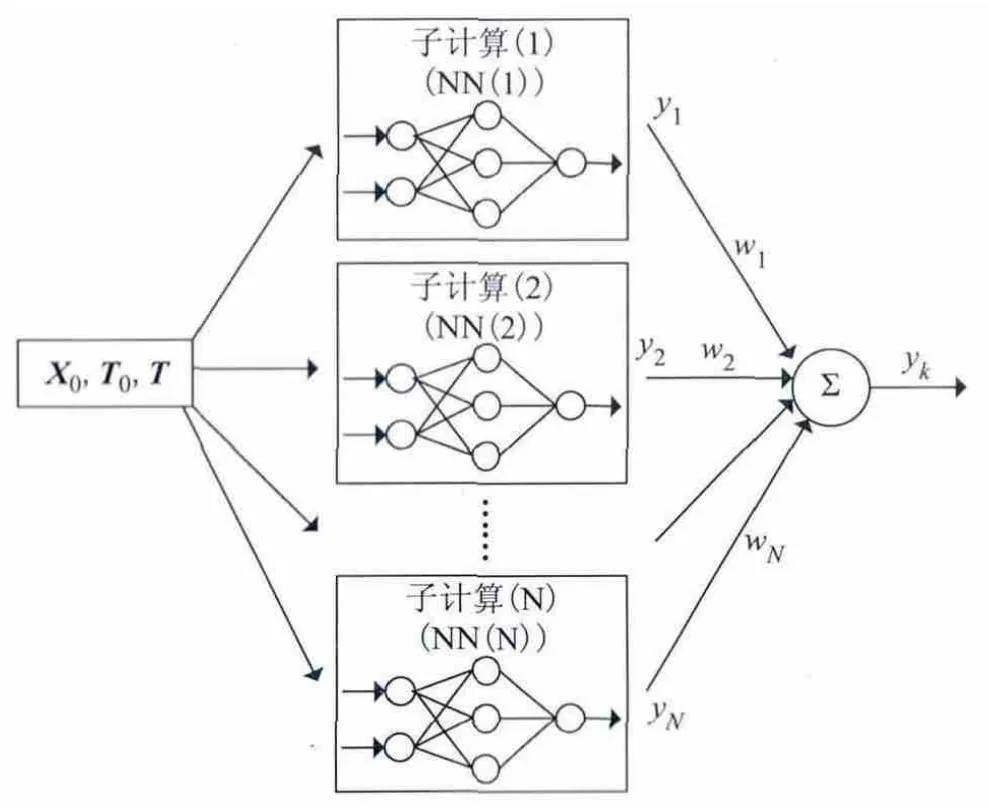
图3 钟差预报的分布式神经网络结构图

钟差预报的分布式神经网络结构如图3所示，图中向量X0、T0和X的含义同图1，模型通信过程也和分布式线性组合预报模型相同；图中模型包含N个子网络模型，NN （i）表示第i个子神经网络；yk为模型输出的第k历元预报钟差值，yi（i＝1，…，N）为各子网络模型的预报值，wik表示模型输出节点与子网络模型的连接权。钟差预报的分布式神经网模型预报过程包括以下主要步骤：1）将已知建模钟差数据交给各个独立的神经网络；2）各个子神经网络对其所得的样本数据进行学习训练，直到满足设定的条件为止；3）将各个子网每个历元输出的钟差预报结果以一定的权值进行加权求和，进而得到最终的钟差预报结果。

对于该模型而言，其涉及到的关键技术主要包括：

（1）子神经网络模型的研究，包括子网络模型的改进、子网络结构的确定和子网络的分布式实现。在众多种类的神经网络中，反向传播模型（back propagation，BP网络）主要用于时间序列的预报［16-17］。但是，BP神经网络却存在着易受局部极值影响而致预报精度不高和网络收敛比较缓慢的不足。针对该模型的不足，许多学者对其改进做了大量的研究，但这些改进主要是针对具体问题在应用时的改进。因此，需要研究预报钟差时对应的BP模型该如何改进，主要包括网络中传递函数和学习训练算法的确定。另一方面，利用人工神经网络解决具体问题时，最关键的是针对具体对象的特点确定合适的网络结构 （网络层数和每层的单元数），所以需要研究适合钟差预报的网络结构。同时由于在神经网络中每层网络中的神经元之间是独立并行处理信息的，这使得子网络本身具备分布式计算的特点，因此需要分析其并行特性，采用分布式计算技术提高子网络学习训练速度，构造出钟差预报的分布式子神经网络。

（2）总网络模型的研究，包括最佳子网数量的确定、各子网络模型间连接权的研究、总网分布式学习算法的设计。

（3）钟差的分布式非线性组合预报模型的研究。关于非线性组合预报方法的研究几乎没有，而人工神经网络可以作为很好的非线性方法组合单一方法的预报结果得到非线性组合预报结果。该方法需要研究的内容主要包括神经网络类型的选取和对应网络模型结构的确定及其算法的分布式实现。

3 结束语

星载原子钟本身复杂的特性和极易受外界环境影响的特点使得精确原子钟运行模型的建立变得非常困难，从而也导致钟差预报变得困难。本文首先总结分析了目前常用的钟差预报模型的相关特性，根据组合预报钟差的思想提出了钟差的分布式预报技术体系，给出了其中所涉及的关键技术及核心研究内容。

理论上该模型能够更好的进行钟差预报，得到更优的预报结果；但在实际应用中，组合权的选取非常关键，如果权值选择不当，该模型的预报优势不能较好的体现出，甚至可能出现预报效果不如单一模型 （因为非线性组合存在劣组合的可能），所以在具体应用本文所提方法进行钟差预报时一定要选择适当的组合权；另外还需注意的是在分布式预报时，具体是采用多线程来实现分布，还是采用多核或者多台互联的计算机，这需要根据所要处理的钟差数据量的多少来决定。最后需要指出的是本文仅给出了该方法的技术体系，其具体实现需要接下来完成。

［1］LEVINE J.A Review of Time and Frequency Transfer Methods［J］.Metrologia，2008，45（6）：162－174.

［2］郑作亚，党亚民，卢秀山，等.附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究［J］.天文学报，2010，51（1）：95－102.

［3］刘利.相对论时间比对理论与高精度时间同步技术［D］.郑州：信息工程大学，2006.

［4］崔先强，焦文海.灰色系统模型在卫星钟差预报中的应用［J］.武汉大学学报：信息科学版，2005，30（5）：447－450.

［5］SENIOR K L，RAY J R，BEARD R L.Characterization of Periodic Variations in the GPS Satellite Clocks［J］.GPS Solution，2008（12）：211－225.

［6］YOUN J H，JEONGHO C，MOON B H.Improving Prediction Accuracy of GPS Satellite Clocks with Periodic Variation Behavior［J］.Measurement Science and Technology，2010（21）：1－8.

［7］朱祥维，肖华，雍少为，等.卫星钟差预报的 Kalman算法及其性能分析［J］.宇航学报，2008，29（3）：966－970.

［8］YUAN Hai－bo，WANG Zheng－ming，DONG Shao－wu，et al.Dynamic Grey－autoregressive Model of an Atomic Clock［J］.Metrologia，2008，45（6）：1－5.

［9］黄观文，杨元喜，张勤.开窗分类因子抗差自适应序贯平差用于卫星钟差参数估计与预报［J］.测绘学报，2011，40（1）：15－21.

［10］ALLAN D W.Time and Frequency（Time－Domain）Characterization，Estimation，and Prediction of Precision Clocks and Oscillators［EB/OL］.［2013－04－20］.http：//tf.boulder.nist.gov/general/pdf/752.pdf.

［11］王继刚.基于GPS精密单点定位的时间比对与钟差预报研究［D］.北京：中国科学院研究生院，2010.

［12］王鹏.法方程层面地球参考框架数据融合及其网格计算应用研究［D］.郑州：信息工程大学，2010.

［13］GHORBANI M A，KHATIBI R，AYTEK A，et al.Sea Water Level Forecasting Using Genetic Programming and Comparing the Performance with Artificial Neural Networks［J］.Computers ＆ Geosciences，2010（36）：620－627.

［14］熊智华，王雄，徐用懋.基于分布式神经网络递推预报误差算法的非线性系统建模［J］.信息与控制，2000，29（5）：414－420.

［15］余凯.基于噪声估计的卡尔曼滤波用于 GPS卫星钟差预报研究［J］.测绘工程，2010，19（2）：29－31.

［16］王琪洁.基于神经网络技术的地球自转变化预报［D］.上海：中国科学院上海天文台，2007.

［17］王宇谱，吕志平.小波神经网络日长预报算法研究［J］.大地测量与地球动力学，2012，32（1）：127－131.