心算对数感发展的影响研究

熊丙章，刘丽颖

(1.西南大学 数学与统计学院，重庆 400715;2.重庆巴蜀中学，重庆 400013;3.重庆工商大学 数学与统计学院，重庆 400067)

1 问题的提出

数感是人的一种基本数学素养，是人对数与运算的一般理解，是主动地，自觉地理解或运用数的态度与意识。随着新课程改革的逐步推进，数感的发展研究日渐引起了人们的重视，相关研究正对此展开。研究表明，数感是一个宽泛的领域，包括估算和心算［1］，二者对数感发展起着极其重要的作用。“灵活地进行心算和估算，判断计算结果的合理性，能创造各种解决数字问题的策略”［2］。不仅如此，“心算还可以提升学生理解数的结构和性质，使学生用具有创造性和独立性的思维去处理数字问题”［3］。时至今日，尽管还没有搞清楚心算在数感发展中到底发挥多大作用，但通过探究数的结构、数与数之间的关系等心算技能为发展数感提供了一种重要方法［4］。鉴于此，我们试图通过考察小学儿童的心算能力对数感的影响来探讨心算在数感发展中发挥的作用。

2 研究方法

2.1 被试

从重庆市主城区的四所小学随机抽取357 名二年级和四年级学生作为被试。其中，二年级男女生各87 和102 名，四年级男女生各77 和91 名。他们的年龄从7 岁到11 岁(M=9.63，SD=0.57)。

2.2 材料及程序

心算活动具有明显的问题大小效应，其加工过程与工作记忆和长时记忆存在密切关系［5］。因此，我们根据教学要求，按照年级从易到难的顺序分别编制了20 道心算题(其中15 道为产生任务型题目，5 道为辨别任务型题目)。数感测试采用了4×3 的被试内容设计，自变量为运算类型(加、减、乘、除)和数字类型(整数、小数和分数)，因变量为答案的正确率、时间和理由，实验共计20 道题目。实验采用个别测试的方法和逐道题目单独呈现的方式，为避免效应，呈现顺序采用了随机方式，由研究者记录答案情况，二者最高可得20 分。

2.3 数据处理

采用Spss 11.0 for windows 进行统计分析。

3 结果与分析

3.1 心算能力对数感水平的影响

一般地，心算是指在没有外在辅助工具的情况下进行的算术运算加工，它是日常生活中一种重要的基本技能和思维活动，其过程可以按照认知活动的信息加工观点分为四个阶段:问题编码、计算、决策和反应执行。在这过程中，有着四种典型的效应［6］:问题大小效应，当问题中的运算数增大时候，获得答案的反应时变长，错误率变高;区分效应，算术问题中越接近正确答案的错误答案较之那些差异大的更难，比如2+5=6 比2+5=10 更难辨别;干扰效应，当呈现的错误答案匹配另一种运算中的正确答案时，比如2+3=6 与2×3=5，错误率会更高，潜伏期也会更长;奇偶效应，当等式呈现的错误答案的奇偶状况与正确答案的奇偶不一样的时候，辨别起来会更快更准确。

评价心算能力一般采用的指标是心算的反应时和正确率。心算的反应时和正确率具有明显的年龄差异，这点在关于心算老年化及其机制的研究中已经得到充分的证实。相关的实证研究还表明，年龄与心算难度存在明显的交互作用，也就是说心算难度的不同导致年龄对反应时和心算效率的影响不同［7］。我们的研究也证实了这一点，结果见表1。

表1 不同年级、性别学生的心算成绩差异性分析

从表1 中可以看出不同年级的儿童的心算成绩差异主效应显著，而性别主效应不显著，年级与性别之间不存在明显的交互作用。我们进一步对不同年级的心算成绩进行了独立样本T 检验，发现在同一年级，随着心算任务难度的增大，正确率明显下降，且反应时间更长，表明心算加工问题大小效应的普遍性。另外我们还给出了不同年级、不同性别学生心算成绩的平均分(M)与标准差(SD)的结果。结果表明，二年级的心算成绩明显不如四年级，差异非常显著(p ＜0.01)。这说明经过小学低、中段对心算的强化训练，到四年级时，小学生心算能力的发展已逐渐上升。在同一年级，虽然简单心算和复杂心算心理机制存在差异，但是总体而言，一定量的联结可以导致较少时间内较好完成任务，足够的练习有助于儿童从计数策略到记忆提取的转变。因此掌握基本的算术知识应该是十分必要的，有利于复杂算术问题的解决。既然速度和记忆是心算能力发展的中介因素，对速度和记忆方面的训练培养应该是有益于包括心算在内的其它认知能力的提高。

有研究观察到，随着儿童年龄的增长，其信息加工速度变快，工作记忆能力亦提高。验证性因素分析表明:［8］儿童加工速度、工作记忆与心算能力三者可能存在一个递进式发展过程。结合被试在心算任务上的表现，我们将心算能力划分为六个水平。按从低到高各个层次的划分标准如下:初始算术水平，被试不能正确完成一位数的简单四则运算;一步计算，一位数运算水平;多步计算，两位数运算水平;多步计算两位数水平;一步计算三位数水平;多步计算三位数计算水平。

我们对不同水平下小学儿童的数感成绩进行了单方向方差检验。表(二)给出了不同水平下儿童数感成绩的平均分和标准差以及F 值。表中结果显示不同心算水平下儿童的数感成绩有明显差异(p＜0.01)。同时我们看到，随着心算水平的提高，儿童的平均数感成绩大体上也有所提高。因此我们进一步对相邻水平之间成绩的差异性进行了T 检验，结果一并列入表2 中。

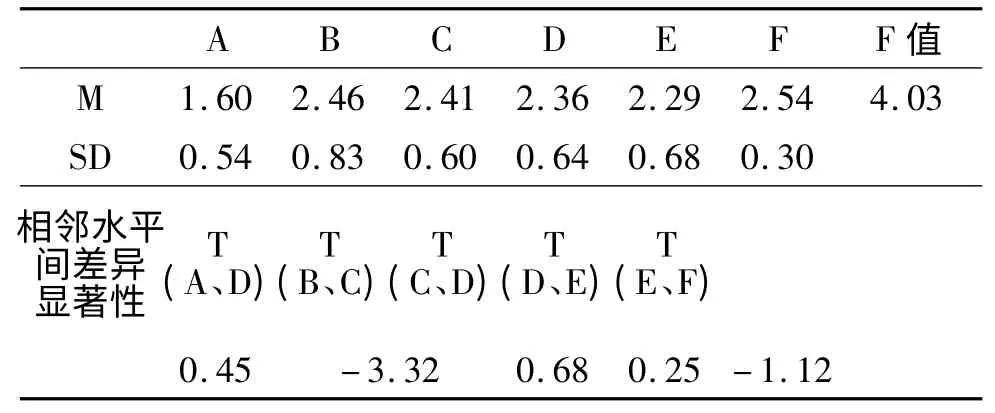
表2 不同心算水平下学生的平均数感成绩及其差异性

从表2 中T 检验的结果看，儿童的数感成绩只在一步计算两位数运算水平同多步计算一位数运算水平之间差异达到极为显著。其他相邻水平间的数感成绩均没有差异。这说明心算水平只在较低水平上对儿童数感有影响。如果我们压迫借助于强化心算教学来发展数感，只有当儿童的心算水平由低级向中级转化之前才最为有效。

我们进一步分析知得出，这两个年级儿童所给数感答案的精确性并没有随着心算水平的提高而明显降低。当他们遇到较困难的问题时倾向于给出误差较大的答案，但他们给出合理答案的比例在各个心算水平上都明显超过不合理的答案的比例，而且数感成绩的总体表现和所用的时间明显受到心算水平的影响。这说明儿童的数感只是在一定程度上依赖于其心算的发展水平，同时它也同问题的特点有一定关系。或许正是这些问题的难度超出了儿童所能接受的限度，从而掩盖了心算水平对数感的影响。

3.2 心算策略对数感策略选择的影响

要完成心算操作，需要两类策略，一类是从记忆中直接提取，另外需要一类类似计数或基于某种规则的运算程序［5］。儿童第一次解决像2+3 这样的简单算术问题时，依靠的是其计数和计数程序方面的知识。这些计数过程或以手指辅助实现(手指计数策略，儿童使用手指代表问题中的数，然后数手指得到答案;计数策略，儿童用手指代表加数，象在默默计算。但得到答案前看不到数手指)，或不用手指(口头计数策略，可以听到儿童计算或动嘴唇)，总体上称为计数策略。

简单的算术问题主要通过以记忆为主的加工来解决，包括算术知识的分解和直接提取。分解策略是把问题分解成若干简单问题。比如，9+8 可以通过从8 减去1 加到9 上，最后把7 与10 相加。采用直接提取策略时，儿童直接说出长时记忆中与当前问题有关的答案，例如当被要求解决5+3 时说出“8”。记忆提取是较好的选择策略，因为提取需要较少时间执行，比其它策略对工作记忆资源要求更少。事实上，从长期记忆中直接提取答案的便捷性强烈影响到儿童心算策略选择。更确切地讲，答案越容易从长期记忆中提取，提取加工更易运用于解决当前问题。

儿童的心算策略对数感发展的影响主要是通过不同策略的使用来体现的。因此我们考察了各种心算水平下儿童对不同数感策略使用频率的百分比。结果见表3。

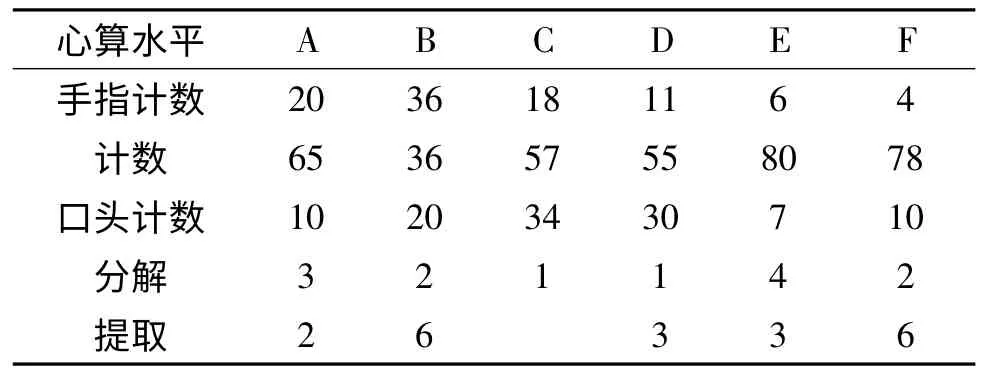
表3 不同心算水平下数感策略的使用频率(%)

从表3 可以看出，不同心算水平下的儿童在进行整数类数感时使用的计数策略相当多。即使在同一心算水平下，儿童也使用了多种策略，而且有所偏重。这也从一个侧面说明心算只是影响数感策略选择的因素之一，个体还考虑了其他因素。我们进一步对同一心算水平下的不同策略使用频率进行了四格表χ2检验，仍然采用只比较在频率大小上相邻的数据。结果发现，在初始算术水平和一步计算两位数运算水平下，小学儿童都没有优势。从多步计算一位数运算水平开始，儿童一直倾向于估算策略，从多步计算两位数运算水平开始，心算成为小学儿童整数类估计的第二选择。因此我们可以认为，不同心算水平的小学儿童大多数情况下都选择有效性中等水平的策略。进一步分析可以看出，不同心算水平的儿童对于同一种策略的使用频率也是有很大差异。总的说来，随着儿童心算能力的提高，粗略估计的使用逐渐降低，心算的使用频率逐渐上升。但随着其他策略的发展，基准策略在一步计算两位数水平上使用急剧下降，随后在其他心算水平又重新加以使用。

随着年龄的增长，算术知识得到不断积累，解答心算问题时计数程序逐渐减少，提取过程使用增加。对儿童解决简单算术问题的研究取得了一些较为明确的结果。

3.4 心算对数感错误类型的影响

我们根据学生的口头报告，并结合他们给出的答案，将他们在数感中所犯的错误划分为五种:猜测错误，对自己给出的答案不能给出理由或报告说“不知道”乱猜的;运算错误，不能正确使用计算规则对数字进行操作;数位错误，将小数点忽略或放错位置;基准错误，错误使用基准“1”或其他基准点;精确错误，个体试图计算出问题的精确答案。我们以此分类标准对儿童在本研究中的错误类型进行了统计分析，以考察心算水平对儿童数感错误的影响。凡是在心算测试中答对题目数为11 个(这是本研究的中位数)或更多的被归为熟练组，而少于11 个题目的归为非熟练组。心算水平不同的儿童在数感中各种错误类型的错误频率见图1。

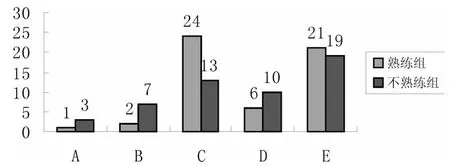
图1 不同心算熟练程度儿童的数感错误类型频率(%)

从表中可以看出，不同心算水平熟练程度的儿童在运算错误和数位错误上存在明显的差异。具体说来，心算不熟练的儿童更容易出现运算上的错误，而心算熟练的儿童更容易出现数位错误，即忽略或者判断答案数字的位数、小数点位置。这一结果说明心算水平对儿童数感的影响主要体现在对运算规则的掌握上，基本规则比较熟练甚至自动化可以减少一些数感错误的发生。而数位的判断相对来说是一种较高层次的技能，是数感培养的重要内容。心算技能是否熟练本身并不能降低数位错误的发生率，它需要儿童的数感得到发展之后才能逐渐减少。

4 结论及启示

儿童的数感只是在一定程度上依赖于其心算能力的大小，他们使用心算策略的种类和优势策略不断变化，大多数情况下儿童倾向于选择中等有效的策略。不同心算水平熟练程度的儿童在运算错误和数位错误上存在明显的差异。从这些结论反观教学，其启示是多方面的。

第一，加强心算教学。心算作为一项基本的数学技能，对数感发展有积极的作用，理应成为数学课程的一个重要部分。不过目前看来心算仍不是中小学数学课的重要组成部分，学生心算技能的发展相当滞后。我们必须采取措施，加强我国中小学的心算教学。如:强化教师的心算意识，消除教师认为心算技能不重要、不值得花费教学时间的误解;恰当安排心算教学内容，使学生受到系统的心算教学，将内容从小学延伸到中学阶段;构建有效的测量工具来评估不同阶段学生心算技能的掌握状况。

第二、在心算教学中培养学生的数感。数感是数的感悟，它表现为对量与数的一种直观能力。学生数感的发展，需要经历感悟多少、用数表示多少、建立数之间的关联、对数进行运算、形成数系概念等的过程。学生学习对多少的感悟，需要在丰富的情境中，充分经历察觉物体集合中所包含的物体数量的多少的过程，积累感知多少的经验。这种对量的多少的觉察往往需要借助于数［8］。因此，在心算教学中，要为学生提供丰富的情景，引导学生通过观察，感悟量的多少，培养儿童能用心算估算出运算结果，并能对结果的合理性作出解释。进而体验和领悟数的意义和表达交流，促进学生数感的发展。

总之，儿童的数感是一个由多种数技能构造的有机整体，对儿童的数感教学，是一个系统的逐渐完善的过程。在儿童发展的不同阶段要相应地增进和发展不同的数感成分，要遵循儿童的年龄特点。

［1］McIntosh A ，Reys B J＆ Reys R E .(1992)A propose framework for examining basic number sense For the Learning of Mathematics，12:2－8.

［2］赵振国.3～6 岁儿童数感发展的研究［J］.心里发展与教育，2008，(4):8－12.

［3］Reys R E.(1984)Mental computation and estimation :past present and future .The elementary School Journal，84(5):547－557.

［3］Reys B J.(1994)Promoting number sense in middle grades.Mathematics Teaching in the middle School，I(2):114－120.

［4］Sowder J T.(1990)Mental computation and number sense.Arithmetic Teacher，37(7):18－20，194.

［5］刘昌，李德明.心算活动机制的研究［J］.心里科学报，1999，(1):111－117.

［6］田云.儿童青少年心算能力的发展及其机制研究［D］.南京师范大学，2004.

［7］刘昌 田云.加工速度、工作记忆与心算能力的发展［J］.南京师范大学报(社会科学版)，2005，(5):90－95.

［8］史宁中 吕世虎.对数感及其教学的思考［J］.数学教育学报，2006，(5):9－11.