波箔径向空气轴承阻力矩研究

刘江，杜发荣

(北京航空航天大学 a.交通科学与工程学院;b.能源与动力工程学院，北京 100191)

近年来涡轮机械具有小型化、高速化的发展趋势，系统转速大幅度提高，轴承作为转子系统的重要部件，其性能直接决定了整个系统的性能优劣。20世纪60年代出现的波箔空气轴承是一种新型自适应动压气体轴承[1]。该轴承高转速、高稳定性的特点，可以很好地满足超高转速的要求。由于波箔径向空气轴承的润滑介质是空气，空气的黏度远远低于润滑油，所以其存在承载能力低，工作范围窄等不足，严重限制了其应用范围。近年对波箔径向空气轴承的研究不断深入，轴承性能不断提高，在微型涡喷、燃气轮机、电脑硬盘及空气循环机中都能够见到其身影[2-3]。

阻力矩是该轴承的一项重要参数，在文献[4-5]进行的试验研究中都涉及了轴承阻力矩的相关工作，但没有深入地对轴承阻力矩的影响因素进行分析。

下文在对一系列不同参数的单片式波箔径向空气轴承进行试验及理论研究的基础上，给出了轴承阻力矩测试数据，并归纳了各参数与轴承阻力矩之间的关系。

1 波箔径向空气轴承

波箔径向空气轴承主要由外壳、波形箔片及平箔片组成(图1)。与传统刚性表面动压气体轴承不同的是，该轴承中由波形箔片和平箔片组成的弹性支承结构可以在气体动压力作用下产生自适应变形，提高轴承稳定性。波形箔片和平箔片的一端共同固定在轴承外壳上，另一端处于自由状态，故轴承弹性支承结构可自由伸缩。

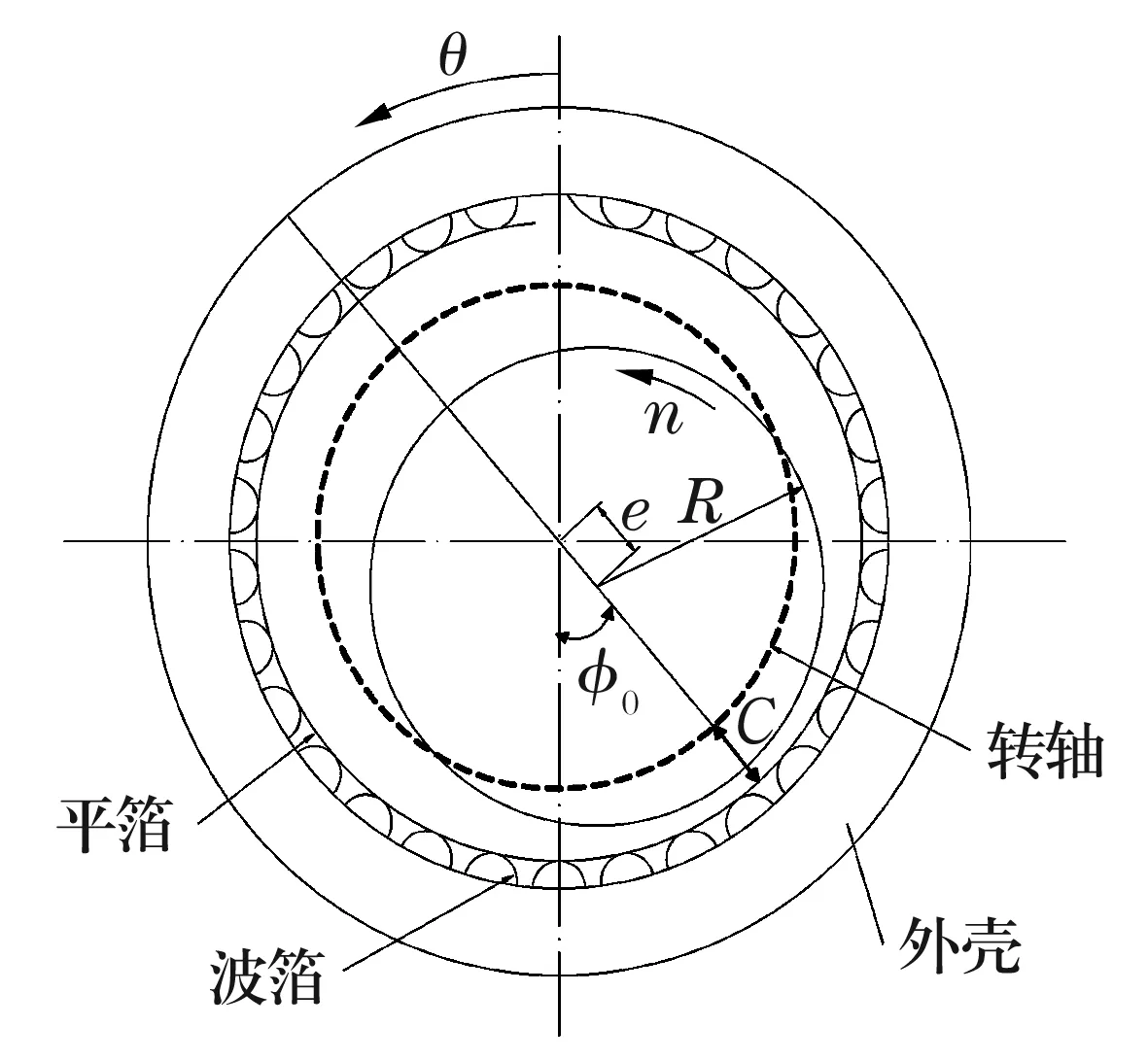
图1 波箔动压径向空气轴承示意图

在此，设计制作了6个弹性支承结构参数各不相同的试验轴承。所有轴承的直径均为32 mm，长度为48 mm。6个试验轴承的弹性支承结构由3种不同参数的波形箔片和2种不同厚度的平箔片相互组合而成。为了保证轴承阻力矩测量具有统一的基准，所有轴承与转轴之间的间隙控制在45 μm以内。

2 波箔径向空气轴承试验台

2.1 试验台设计[6]

波箔径向空气轴承整个试验装置布置在1个800 mm×800 mm的铸铁平台上。试验台采用转轴固定旋转、轴承在转轴上悬浮工作的原理，可以在不影响轴承正常工作的前提下，对轴承施加载荷，对轴承的阻力矩、2个方向的位移、转速及温度进行测量。试验台最高转速为60 000 r/min。

2.2 阻力矩的测量

对轴承各工况阻力矩的精确测量是进行阻力矩试验研究的基础。阻力矩测量单元如图2所示。通过一个固定在轴承座上的测量杆，将轴承阻力矩的变化转变为测量钢索中拉力的变化。通过精密测力传感器对钢索拉力的变化进行测量。

轴承启动及停车过程中钢索的拉力变化如图3所示。确定测量力臂长度后，便可方便地计算得到轴承的阻力矩。对于轴承稳态阻力矩的测量，只需记录轴承静止与稳态工作时拉力的差值，便可计算得出轴承的稳态阻力矩。

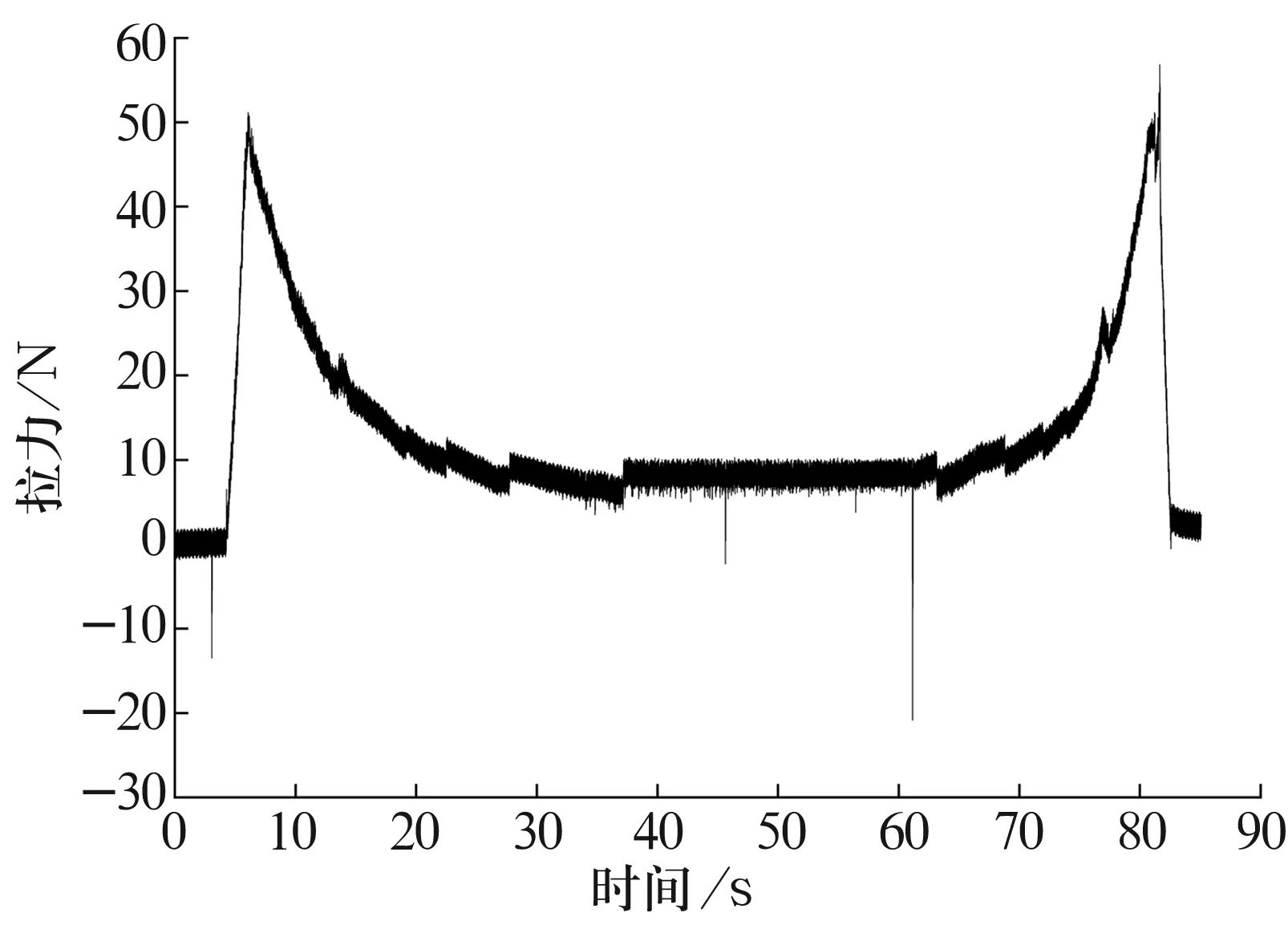
图3 1#轴承启动、停车过程的拉力(轴承载荷W=32 N)

3 试验结果分析

3.1 启动及停车过程最大阻力矩

以1#，2#，3#，5#轴承为例，轴承在启动及停车过程中的最大阻力矩如图4～图7所示。试验共测量了12～72 N的7个载荷点的数据。从所列4个试验轴承的数据可见，波箔径向空气轴承在启动和停车过程中的最大阻力矩与轴承载荷成线性关系。并且所列的4个试验轴承在12 N载荷点的阻力矩都在 150 N·mm左右，而72 N载荷点的阻力矩都在450N·mm左右，这证明波形箔片的突起宽度和平箔片的厚度对轴承启动及停车过程最大阻力矩影响很小。

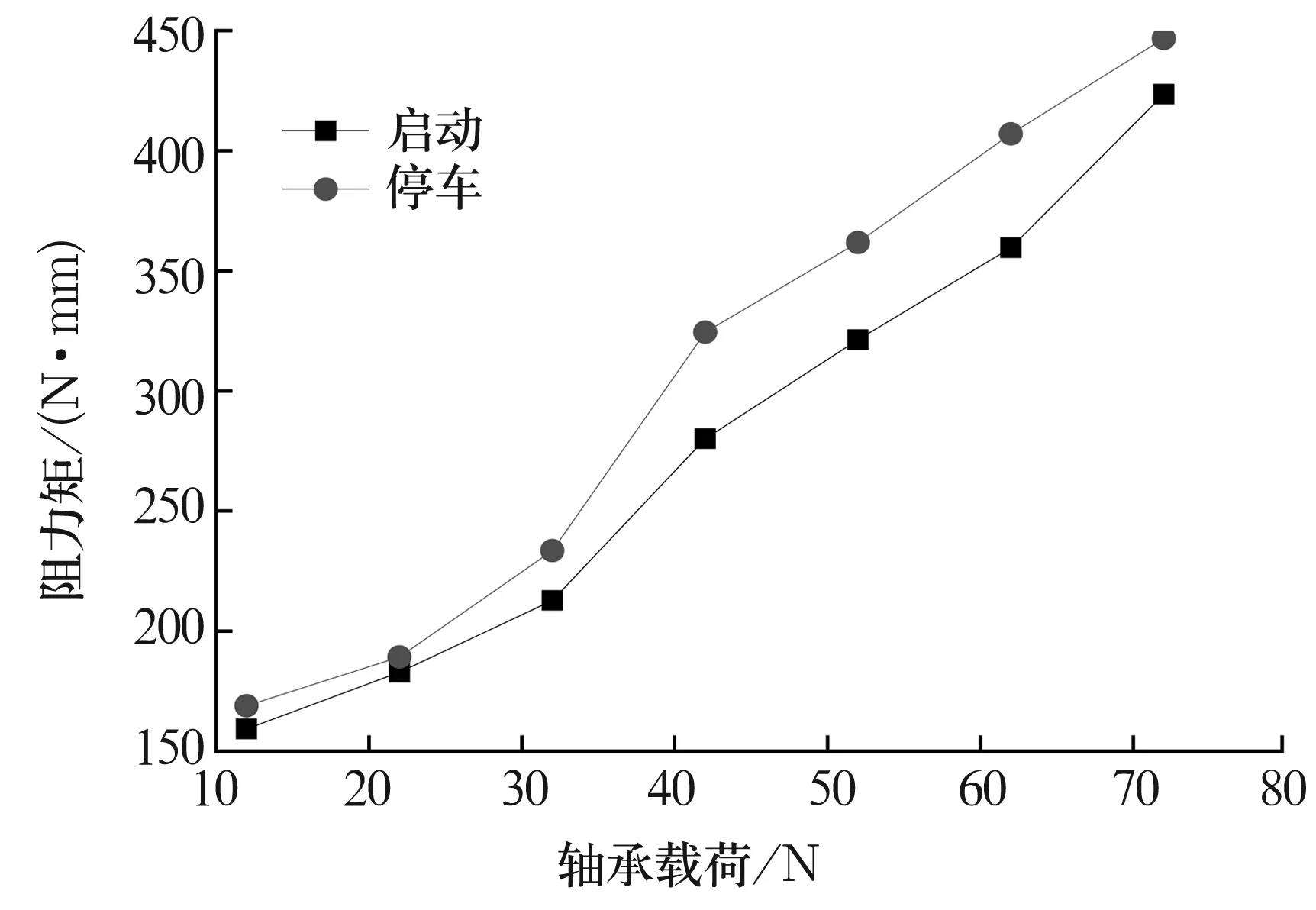
图4 1#轴承启动及停车过程最大阻力矩

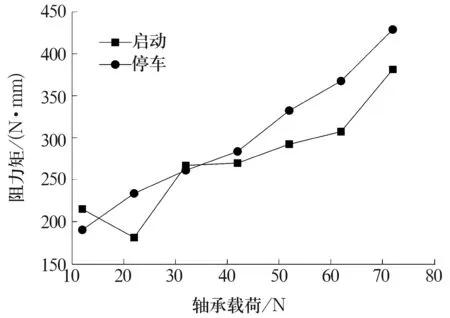
图5 2#轴承启动及停车过程最大阻力矩

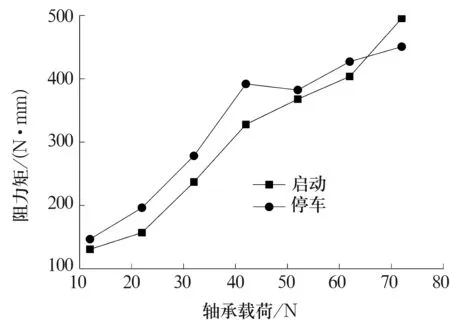
图6 3#轴承启动及停车过程最大阻力矩

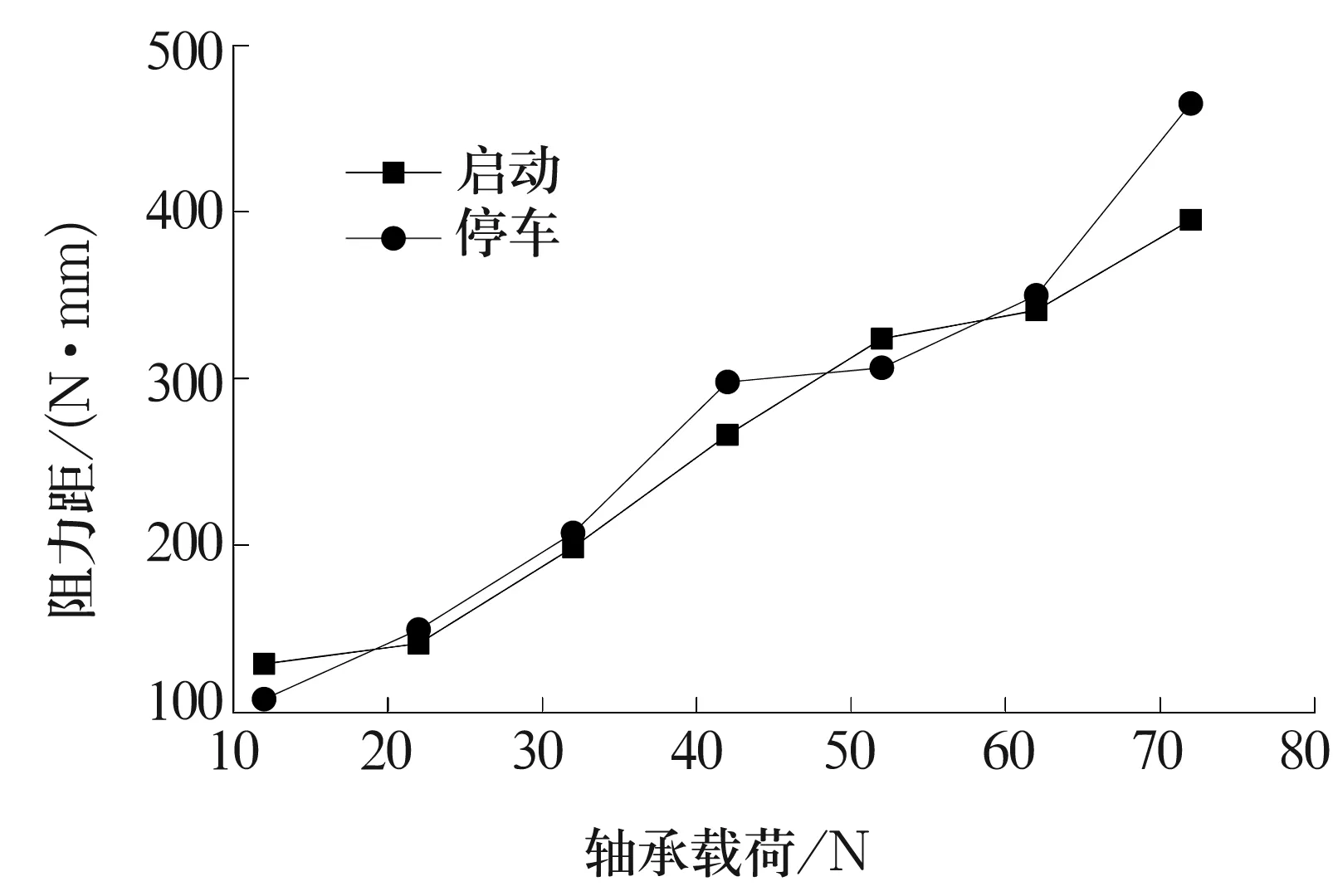
图7 5#轴承启动及停车过程最大阻力矩

从试验数据中还可发现，同等载荷轴承在停车过程中的最大阻力矩比启动过程的最大阻力矩平均高出15%，所以轴承在停车过程中的温度控制必须引起重视，防止温度过高使轴承损坏。

3.2 稳态阻力矩

1#～6#轴承30000r/min时各载荷阻力矩如图8所示。在所测量的12～57 N载荷范围内，所有试验轴承的阻力矩都在29 N·mm左右，轴承载荷的变化对阻力矩的影响很小。

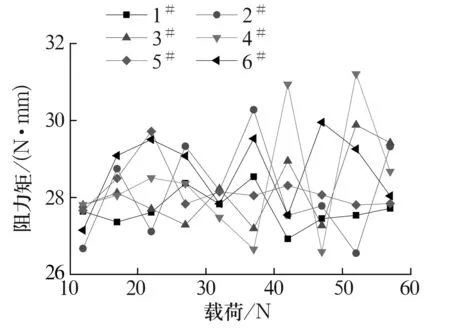
图8 1#～6#轴承各载荷阻力矩(轴承转速n=30 000 r/min)

1#～6#轴承42 N载荷下各转速时的阻力矩如图9所示。在18 000～54 000 r/min转速范围内，轴承阻力矩保持在29 N·mm左右，转速变化对轴承阻力矩的影响非常小。

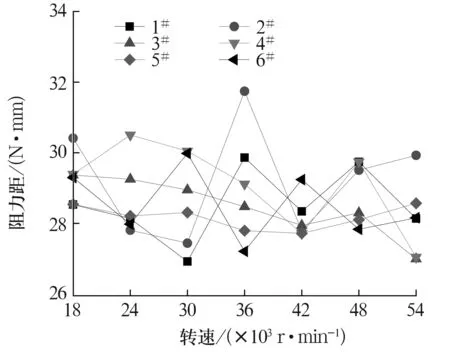
图9 1#～6#轴承各转速阻力矩(轴承载荷W=42 N)

从图8和图9中可发现，轴承的阻力矩没有因其结构参数的不同而发生变化。无论是波形箔片突起宽度，还是平箔厚度发生变化的轴承，阻力矩都在同一水平。

4 理论模型的建立与求解

波箔径向空气轴承内部工作过程是一个复杂的流固耦合问题，既要考虑气体动压润滑部分，也需同时考虑轴承弹性支承结构在气体动压力作用下的变形。

在图1所示波箔径向空气轴承圆柱坐标系下，气体润滑Reynolds方程为

(1)

式中：R为轴承半径；p为气膜压力；h为气膜厚度；μ为空气的绝对黏度；U为轴承线速度(式中所有物理量统一采用国际单位)。

对于弹性支承结构在气体动压力下的变形，采用三维有限元软件ABAQUS进行计算。轴承弹性支承结构的三维有限元模型如图10所示，模型将弹性支承结构展开成平面，共计86 880个六面体单元，115877个节点。箔片间的摩擦因数设置为0.2。施加在平箔表面上的压力为0～0.3 MPa，每间隔0.03 MPa分别施加，分10个载荷步计算得到各压力作用下平箔表面的变形。基于计算结果，通过插值便可得到计算压力范围内所有压力点的变形情况，满足波箔径向空气轴承模型求解的需要。

气体润滑Reynolds方程与弹性支承结构的有限元模型通过轴承的气膜厚度方程耦合到一起。根据图1所示几何关系，波箔径向空气轴承气膜厚度方程为

h=C+ecos(θ-φ0)+Wf，

(2)

式中：C为轴承半径间隙；e为转轴的偏心量；φ0为气膜最小厚度方向与x轴正方向的夹角；Wf为轴承弹性支承结构在动压力作用下产生的径向变形。

与传统刚性支承表面空气动压轴承气膜厚度方程相比，波箔径向空气轴承气膜厚度方程增加了弹性支承结构变形量Wf。

设定轴承动压力的迭代初值后，便可通过弹性支承结构有限元模型计算得出此压力下的变形，基于弹性支承结构的变形量可求解气膜厚度方程，在轴承气膜厚度的基础上即可求解气体润滑Reynolds方程，获得轴承动压力的新值。如此循环迭代便可求得波箔径向空气轴承的动压力分布情况。1#轴承气膜动压力分布如图11所示。

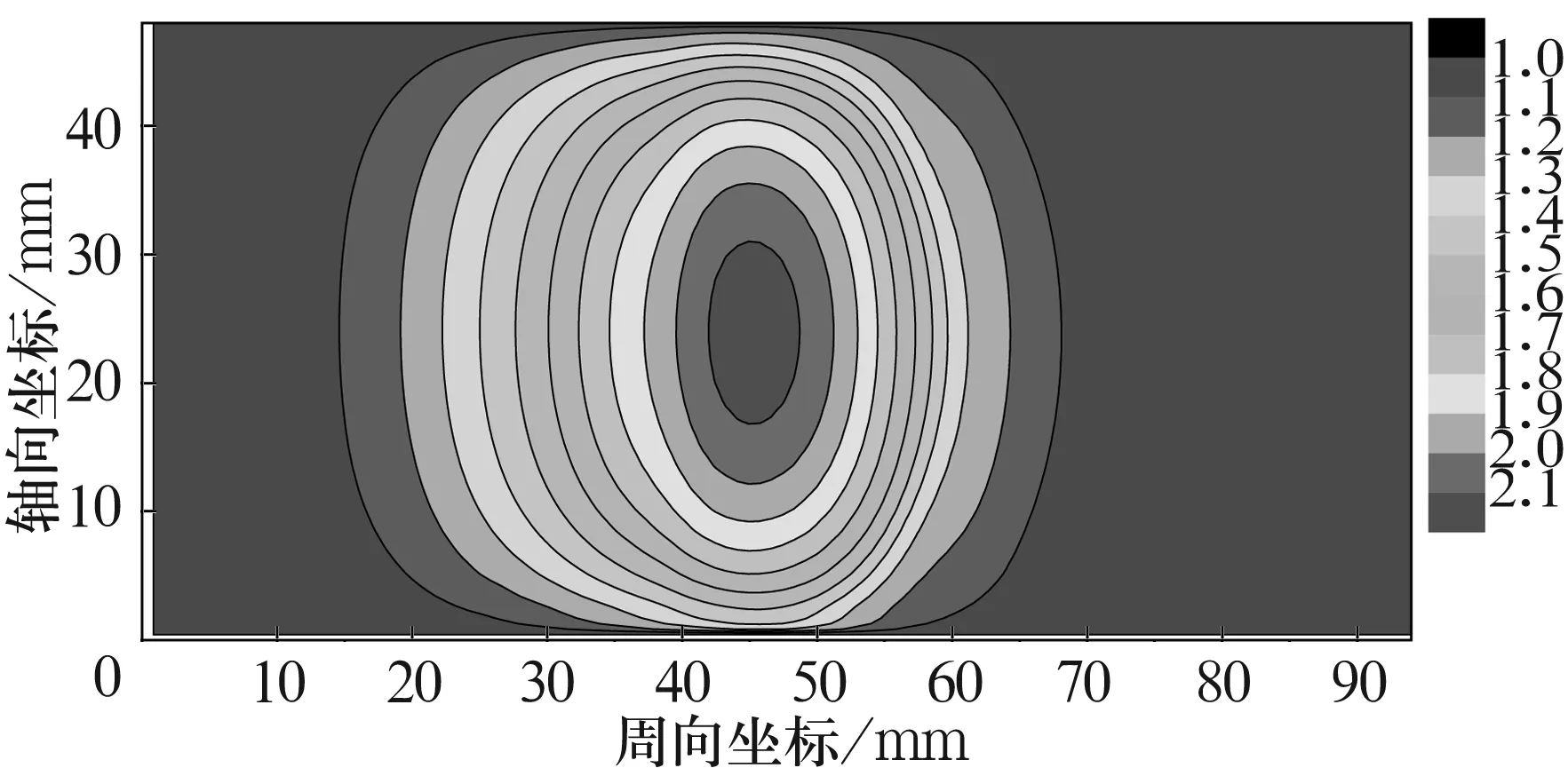
图11 1#轴承气膜动压力分布(n=30 000 r/min,μ=0.7)

基于波箔径向空气轴承动压力分布情况，轴承的阻力矩为

(3)

波箔径向空气轴承理论模型的特点在于使用三维有限元法对弹性支承结构的变形进行了计算，完全考虑了平箔片的凹陷、波形箔片各突起间的相互影响、平箔片与波形箔片间的摩擦、波形箔片与轴承外壳间的摩擦等因素[7]。与传统的波箔径向空气轴承模型相比，排除了弹性支承结构建模过程中的简化导致的误差，计算精度进一步提高。

5 计算结果分析

5.1 轴承载荷对阻力矩的影响

在波箔径向空气轴承理论模型的求解过程中，不同的偏心率对应着轴承不同的承载力，即轴承载荷。以1#，3#，5#轴承为例，各偏心率下阻力矩的计算结果如图12所示，随着偏心率的增大，轴承的阻力矩也随之增加，当偏心率由0.2增加到0.7时，3个试验轴承阻力矩由29.4 N·mm增加到37.2 N·mm，增加了26.5%。从图中还可以看到随着偏心率的增加，轴承阻力矩的增长率越来越大，偏心率由0.2增加到0.3，相应的阻力矩增加0.5 N·mm左右，增幅约为17.7%，而当偏心率由0.6增加到0.7时，阻力矩增加3 N·mm左右，增幅约为8.8%。

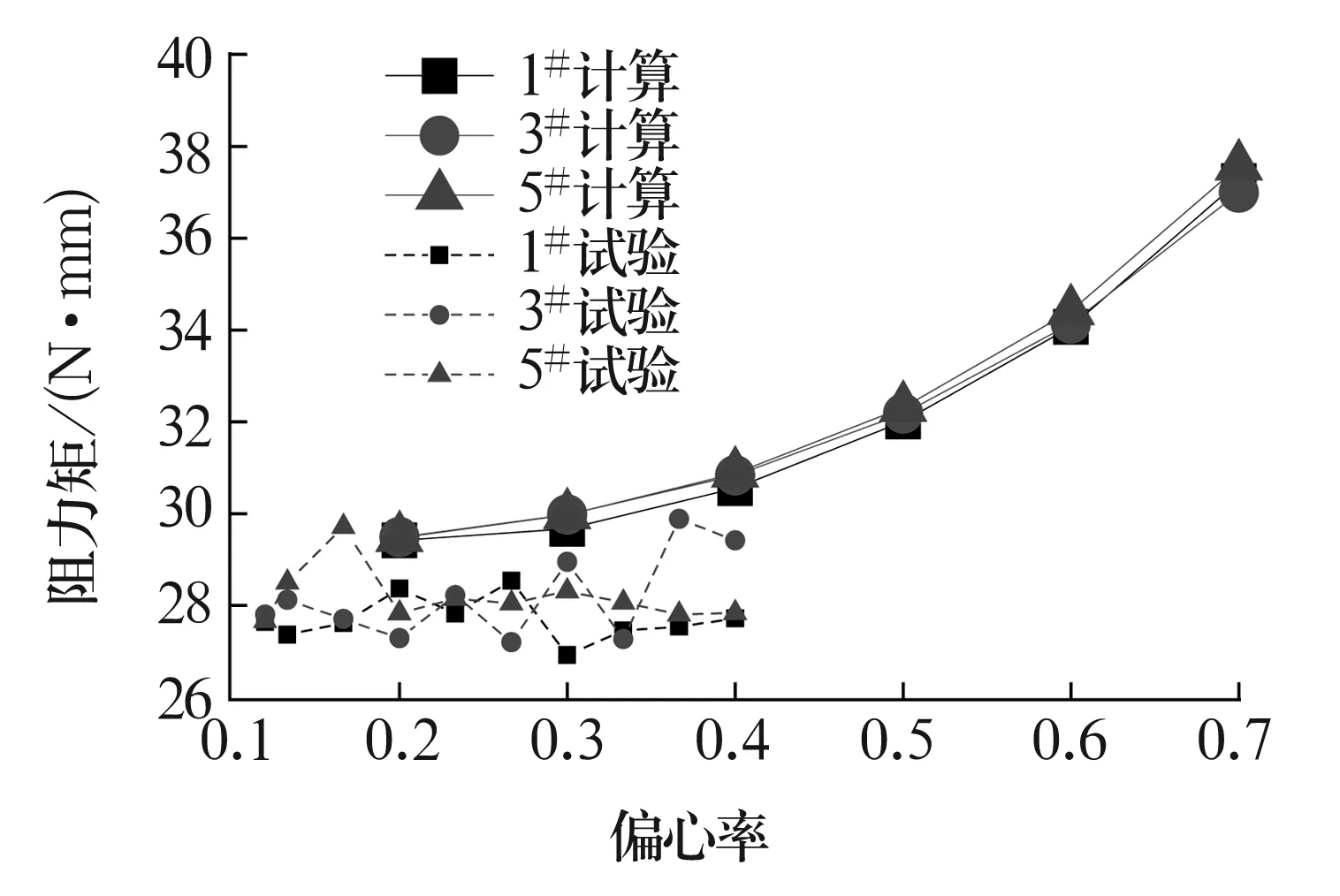
图12 1#，3#，5#轴承各偏心率阻力矩(n=30 000 r/min)

通过计算各偏心率下轴承的承载力，即可将轴承各载荷下阻力矩的试验数据与计算数据进行对比(图12)，在试验测量区间内，计算值比试验值大10%左右，属于可接受范围。

5.2 轴承转速对阻力矩的影响

以2#，4#，6#试验轴承为例，偏心率为0.5时各转速的阻力矩如图13所示。3个轴承的阻力矩计算数据在各个转速点几乎相同，转速从12 000 r/min增加到54 000 r/min过程中轴承的阻力矩维持在30 N·mm，只是前3个转速点的阻力矩略高。

图13 2#，4#，6#号轴承各转速下的阻力矩(μ=0.5)

通过计算值与试验值对比，计算值比试验值大10%左右，属于可接受范围(图13)。因此，证明文中建立的波箔径向空气轴承模型的精度是可信的。

6 结论

(1)波箔径向空气轴承启动及停车过程最大阻力矩与轴承载荷成正比，并且轴承结构参数对启动及停车过程最大阻力矩的影响可以忽略。

(2)同等载荷下，轴承在停车过程中的最大阻力矩比启动过程的最大阻力矩平均高出15%。

(3)波箔径向空气轴承稳态阻力矩随着轴承载荷的增大而增大，并且增幅逐渐增大；而转速与轴承结构参数对稳态阻力矩的影响非常小。

(4)弹性支承结构三维有限元模型与流体润滑Reynolds方程耦合建模的方法是可行的，计算结果可信。