一类双参数类四次三角Bézier曲线及其扩展
2013-07-20喻德生徐迎博曾接贤
喻德生,徐迎博,曾接贤
1.南昌航空大学 数学与信息科学学院,南昌 330063
2.南昌航空大学 软件学院,南昌 330063
一类双参数类四次三角Bézier曲线及其扩展
喻德生1,徐迎博1,曾接贤2
1.南昌航空大学 数学与信息科学学院,南昌 330063
2.南昌航空大学 软件学院,南昌 330063
曲线曲面的表示是计算机辅助几何设计中的一个重要的研究课题。Bézier曲线和B样条曲线[1]因其结构简单、直观而被广泛应用于曲线造型中。但它们也有一定的局限性:(1)曲线形状调整不方便;(2)不能精确地表示圆弧等二次曲线。虽然NURBS曲线解决了这些问题,但其求导和求积分的过程复杂,并且权因子的选择问题至今并未解决。为了克服它们在造型方面的不足,人们对带形状参数的多项式曲线和三角多项式曲线进行了研究。文献[2]用基函数sint,cost,t,1构造了C曲线,它具有许多与Bézier曲线类似的性质,还可以精确地表示圆弧和圆柱。文献[3-5]用不同方法对Bézier曲线进行了扩展,扩展曲线保留了Bézier曲线的优良性质,具有更灵活的形状可调性和更好的逼近性,并且参数的几何意义明显。文献[6-9]分别对带形状参数的三角多项式曲线和双曲多项式曲线进行了研究。该类曲线除了具有简单的表示形式、灵活的可调性外,在一定条件下可以精确地表示某种二次曲线。文献[10]是对文献[8]在次数上的推广,由带形状参数的类三次曲线推广到带形状参数的类四次三角多项式曲线。文献[11-15]对各类样条曲线的性质和应用进行了研究。文献[16]用基函数1,sint,cost,sin2t构造了可调的类三次参数曲线。该类曲线与三次Bézier曲线相比,更简单更具表现力,可以精确表示椭圆和抛物线等曲线。文献[17]利用一个对称的调配函数,结合NURBS曲线中权的思想,在曲线控制顶点处引入调配参数,对一类有理样条曲线进行了扩展,扩展曲线比原曲线描述能力更好,并且包含了原曲线的形式。
本文给出带两个形状参数的类四次三角Bézier曲线及其扩展曲线的定义,得到了该类曲线及其扩展曲线的性质,给出了两段带两个形状参数的类四次三角Bézier曲线G1(C1),G2(C2)及两段扩展曲线G1(C1),G2(C2)光滑拼接的充要条件,并结合实例分别说明该曲线及其扩展曲线在曲线造型,特别是在非对称图形的造型中的应用。
1 带两个形状参数的类四次三角Bézier曲线
1.1 曲线的定义
定义1设实数λ,μ∈[-1,1],t∈[0,π/2],则称关于t的三角多项式:
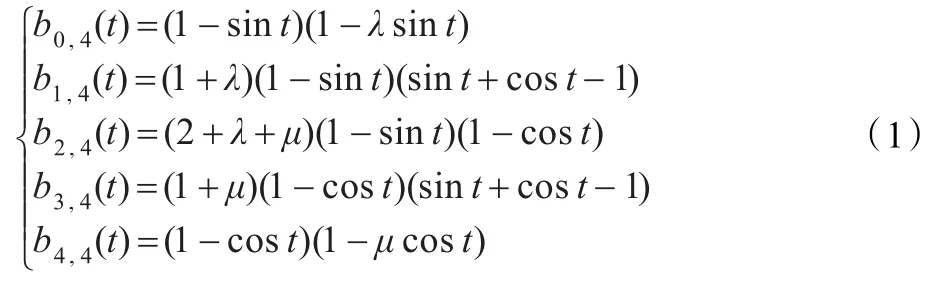
为带参数λ,μ的类四次三角多项式基函数。
特别地,当λ=μ时,式(1)即为文献[10]中的基函数。
由式(1)可知基函数具有如下性质:
(1)非负性,即bi,4(t)≥0,t∈[0,π/2]。
(3)对称性,即bi,4(t;λ,μ)=b4-i,4(π/2-t;μ,λ)。
(4)端点性质
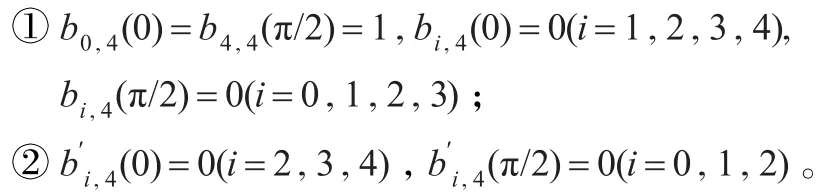
(5)最大值,即每个基函数在[0,π/2]上有一个最大值。b0,4(t)的最大值在t=0处,b1,4(t)的最大值在(0,π/4)内,b2,4(t)的最大值在t=π/4处,b3,4(t)的最大值在(π/4,π/2)内,b4,4(t)的最大值在t=π/2处。
图1为当λ=0.5,μ=1时5个基函数的图形。
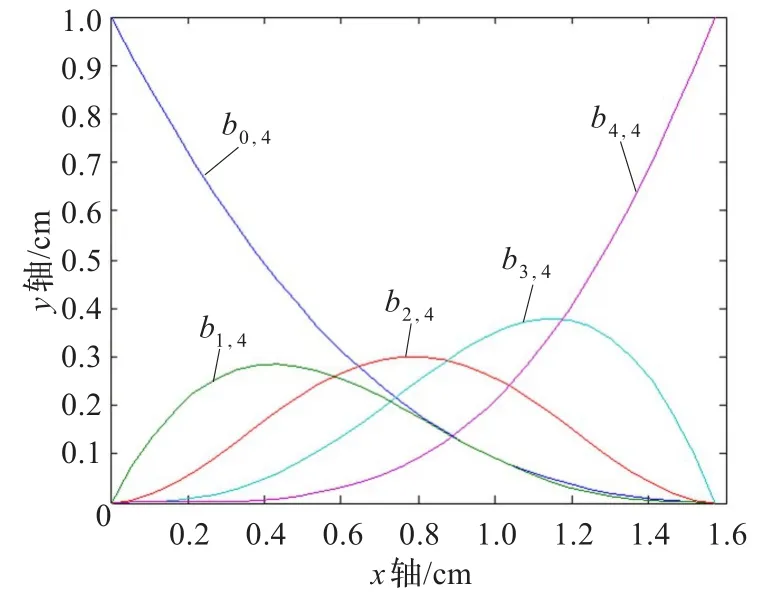
图1 基函数的图形(λ=0.5,μ=1)
定义2给定5个控制顶点Pi∈Rd(d=2,3,i=0,1,2,3,4)。设t∈[0,π/2],则称:

所定义的曲线为带两个形状参数的类四次三角Bézier曲线(下面简称推广曲线)。
1.2 曲线的性质
(1)端点性质。由基函数的端点性质得:
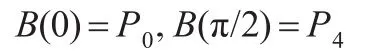
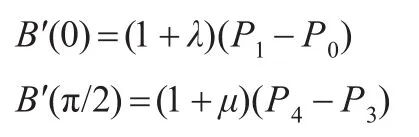
即曲线具有与四次Bézier曲线完全相同的端点性质:插值于首末端点并且在首末端点处与控制多边形相切(如图2)。
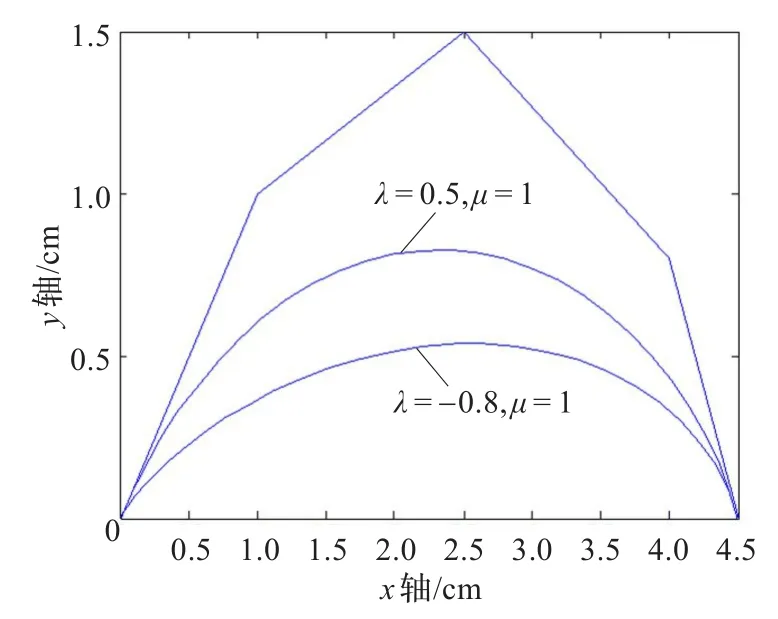
图2 扩展的类四次三角Bézier曲线
(2)对称性。保持控制顶点的位置不变,只是把它们的次序完全颠倒,那么曲线在下列意义上是对称的:
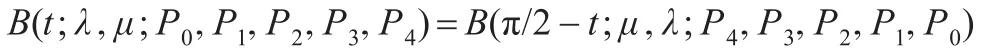
(3)几何不变性和仿射不变性。曲线形状仅与控制顶点有关而与坐标系的位置和方向无关,即曲线的形状在坐标平移和旋转后不变。
(4)凸包性。由基函数的非负性知,曲线是落在由控制顶点生成的凸包之内的。
(5)平面类四次三角Bézier曲线的变差缩减的性质。这里采用文献[8]所提供的证法。首先证明基函数组{b0,4,b1,4,b2,4,b3,4,b4,4}在 (0,π/2)上满足笛卡尔符号法制,即对任意一组常数序列{c0,c1,c2,c3,c4},有:
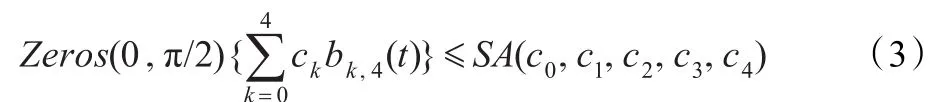
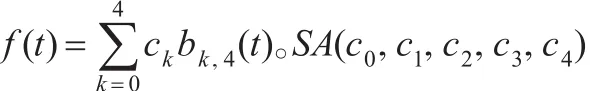
不妨设c0>0,SA(c0,c1,c2,c3,c4)的可能取值为 4,3,2,1,0。
①当SA(c0,c1,c2,c3,c4)=4时,则c4>0。另一方面,假设f(t)在 (0,π/2)上有5个根,则由f(0)=c0,f(π/2)=c4且f(t)在[0,π/2]上连续,必有f(π/2)=c4<0,这与c4>0矛盾,故式(3)成立。
②当SA(c0,c1,c2,c3,c4)=3,2,1时,同理可证式(3)成立。
显然SA(c0,c1,c2,c3,c4)=0时式(3)成立。故结论成立。
下面证明变差缩减性质成立。
设一直线L与控制多边形的PkPk+1边交于点Q,其中PkPk+1边的法向量为v。则Pk,Pk+1分别位于直线L的两侧,即v·(Pk-Q)和v·(Pk+1-Q)符号相反。因此与L交点的个数,而B(t)与L交点个数为所以由基函数组的笛卡尔符号法则B(t)与L交点的个数 ≤SA{v· (P0-Q),v·(P1-Q),v·(P2-Q),v·(P3-Q),v·(P4-Q)},从而结论得证。
(6)保凸性。由性质(5)知,当控制多边形是为凸时,平面类四次三角Bézier曲线为凸曲线。
(7)形状参数对曲线形状的影响。给定控制顶点P0,P1,P2,P3,P4,由定义2即定义了带有两个形状参数的类四次三角Bézier曲线。由基函数的定义及性质可知,则当λ(μ)固定且μ(λ)不断增大时,曲线逐步靠近控制多边形的P2P3(P1P2)边;当λ和μ的值同时增大(减小)时,曲线整体的靠近控制多边形(整体靠近线段P0P4)(如图3);当λ增大μ减小(λ减小μ增大)时,曲线被拉向P1P2(P2P3)边,且拉伸的效果显著。特别地,当λ=μ=-1时,三角多项式曲线退化为连接P0P4的线段。由此可见,与带一个形状参数的类四次三角Bézier曲线相比,带两个形状参数的类四次Bézier曲线对曲线有更好的局部调整能力。
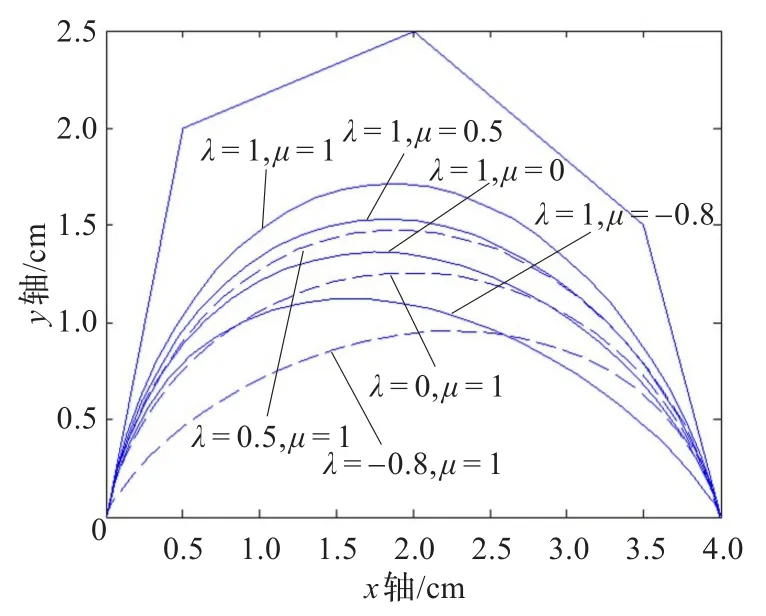
图3 参数对曲线形状影响
图3中实线从上往下参数(λ,μ)取值依次为:(1,1),(1,0.5),(1,0),(1,-0.8);虚线从上往下参数(λ,μ)的取值依次为:(0.5,1),(0,1),(-0.8,1)。
1.3 曲线的拼接
本节考虑两段推广曲线的拼接问题,设:
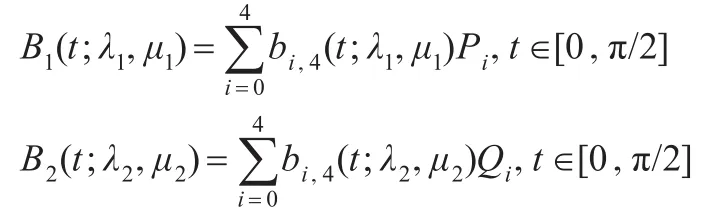
分别为由控制顶点Pi,Qi(i=0,1,2,3,4)定义的带两个形状参数的类四次三角 Bézier曲线,其中λ1,μ1,λ2,μ2∈[-1,1]。
定理1带两个形状参数的类四次三角Bézier曲线B1(t;λ1,μ1),B2(t;λ2,μ2)在连接点P4=Q0处达到G1光滑拼接(C1光滑拼接)的充要条件是:

其中δ1>0(δ1=(1+μ1)/(1+λ2))。
事实上,要使两曲线B1(t;λ1,μ1),B2(t;λ2,μ2)在连接点P4=Q0处达到G1光滑拼接,则在连接点处有公共的切矢方向,即存在常数δ1>0,使:
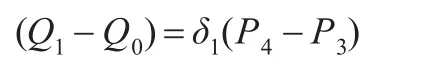
将Q0=P4代入化简即得式(4)。
特别,当δ1=(1+μ1)/(1+λ2)时,有下式成立:
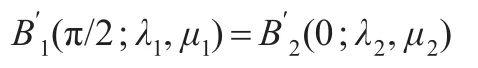
即两曲线在连接点处有公共的切矢,因此两曲线连接点P4=Q0处达到C1光滑拼接。
由定理1知,两段推广曲线C1光滑拼接仅与其中的μ1和λ2有关,与λ1,μ2无关。故调整参数λ1,μ2可以在不改变拼接曲线连续性的情况下对曲线的形状进行微调,这是带一个形状参数的类四次三角Bézier曲线无法做到的,如图4。
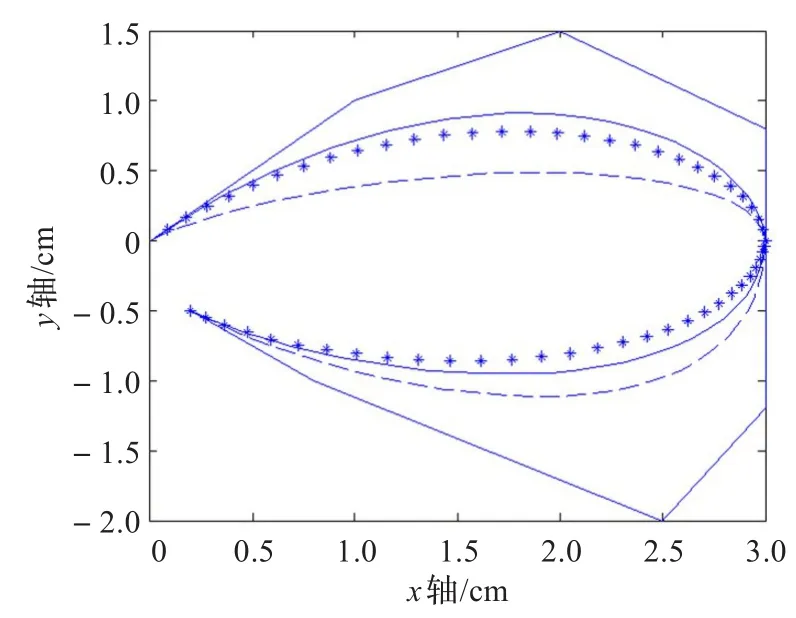
图4 两段曲线的C1拼接及形状调整
下面给出两段曲线G2(C2)光滑拼接的条件。记P3P4与(1-λ1)P0+(2+λ1+μ1)P2-(3+μ1)P3及P3P4与(1-μ2)Q4+ (2+λ2+μ2)Q2-(3+λ2)Q1组成的平行四边形的面积分别为S1,S2。
定理2两段带两个形状参数的平面类四次三角Bézier曲线B1(t;λ1,μ1),B2(t;λ2,μ2)在连接点P4=Q0处达到G2光滑拼接的充要条件是除定理1中G1光滑拼接条件外,还满足:

其中τ=(1+λ2)δ1/(1+μ1),且P2,Q2在公切线的同一侧。
证明两曲线B1(t;λ1,μ1),B2(t;λ2,μ2)在连接点处要达到G2光滑拼接,首先必须达到G1光滑拼接,因此要满足定理1中相应条件;其次在连接点处要有相等的曲率矢。由于两曲线在公共点的曲率为:
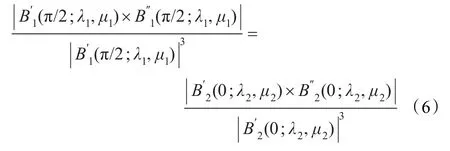
经计算有:
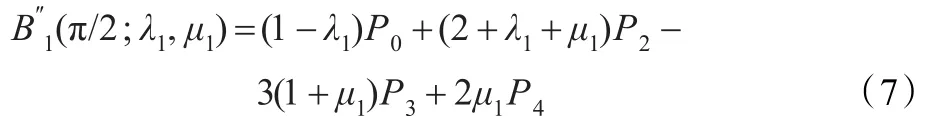
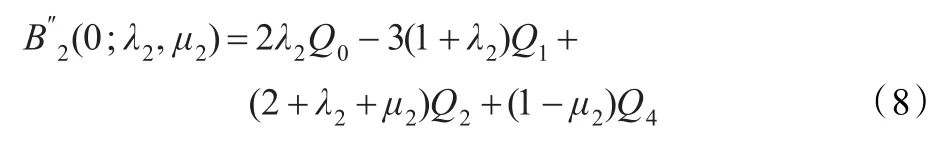
根据曲线的端点性质,并将式(7)、式(8)代入式(6)化简即得式(5)。
定理3两段带两个形状参数的平面类四次三角Bézier曲线B1(t;λ1,μ1),B2(t;λ2,μ2)在连接点P4=Q0处达到C2光滑拼接的充要条件是除C1光滑拼接条件外,还满足下式:
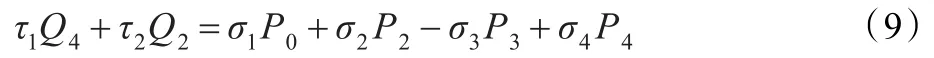
其中τ1=1-μ2,τ2=2+λ2+μ2,σ1=1-λ1,σ2=2+λ1+μ1,σ3= 6(1+μ1),σ4=6+5μ1+λ2。
证明两曲线B1(t;λ1,μ1),B2(t;λ2,μ2)要在连接点处达到C2光滑拼接,首先必须达到C1光滑拼接,因此要满足定理1中相应条件;其次要求二阶导矢相等,即

将C1光滑拼接条件及式(7)、式(8)代入上式化简即得式(9)。
1.4 曲线的应用
当μ=λ时,推广曲线即为文献[10]中曲线,此时曲线可以精确表示椭圆(圆)、抛物线和心脏线。下面用例子来说明在不改变控制多边形的情况下,两个形状参数在曲线形状微调上的应用。
例1图5和图6是用推广曲线生成的开花瓣和闭花瓣图形,这种功能与带一个形状参数的的类四次三角Bézier曲线类似。但推广曲线不需要通过修改控制顶点,只要改变λ,μ的值就可以生成局部对称(λ=μ)和非局部对称(λ≠μ)的花瓣图形(如图7和图8),这种功能是带一个形状参数的的类四次三角Bézier曲线不具备的。
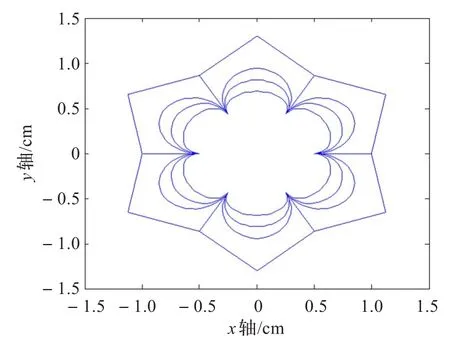
图5 曲线所生成的对称开花瓣图形
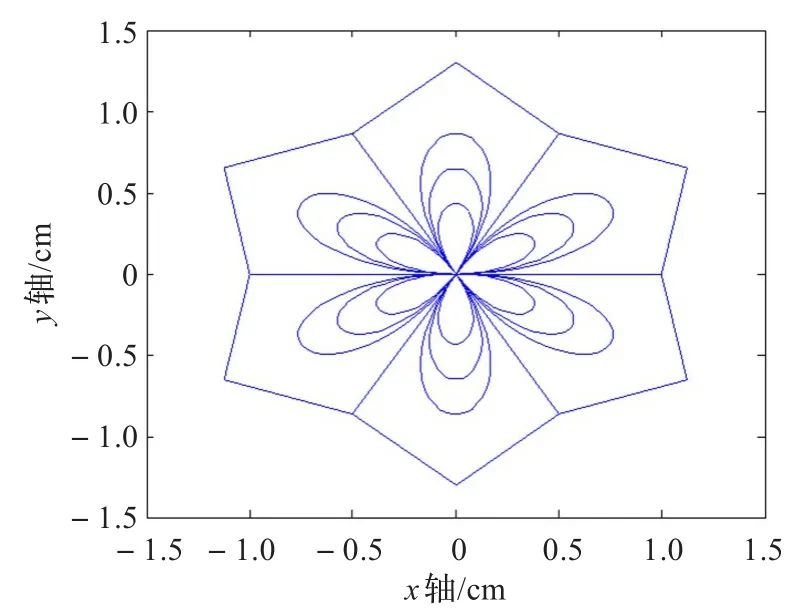
图6 曲线所生成的对称闭花瓣图形

图7 当λ≠μ时调整形状参数生成的花瓣图形
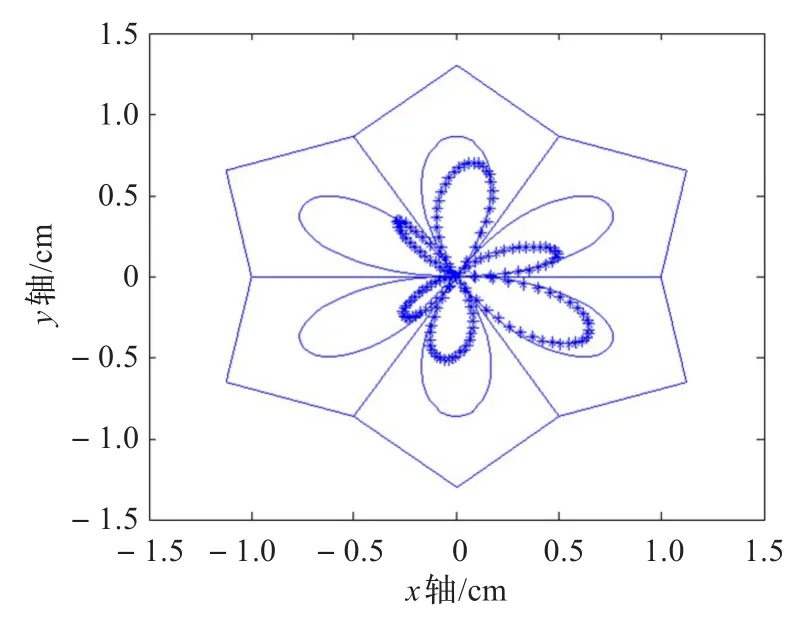
图8 对于每段的λ和μ分别调整生成的花瓣图形
可见,在曲线造型中使用带两个形状参数的类四次三角Bézier曲线比较方便,形状修改十分简单,特别是在生成不对称图形方面具有独特功能,而且灵活、多样。
例2推广曲线具有更强的灵活性和微调能力。如图9(a)为λ=μ时,推广曲线(即文献[10]中的曲线)的实物花瓣造型及形状调整,不改变控制多边形,调整参数值得到的是一系列同心的花瓣图形,此时实际上只有一个参数可以调整,灵活性和调整效果较弱;图9(b)为λ≠μ时,推广曲线的造型及形状调整,不改变控制多边形,可任意调整λ,μ值(λ≠μ)得到不同心的图形,灵活性和调整效果较好。
2 扩展曲线的定义、性质及应用
2.1 扩展曲线的定义
为了引出扩展曲线的定义,首先引进一个调配函数f(t)=cos2t,以及由它产生的另外一个函数
设Pj(j=0,1,2,3,4)为带两个形状参数的类四次三角Bézier曲线的五个控制顶点。记:
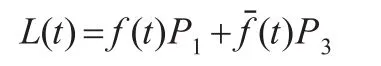
则称L(t)为局部调控函数。
定义3设Pi∈Rd(d=2,3,i=0,1,2,3,4)为给定的五个控制顶点,0≤α≤1,t∈[0,π/2],则称:

为带两个形状参数的类四次三角Bézier曲线的扩展曲线,简称扩展曲线。
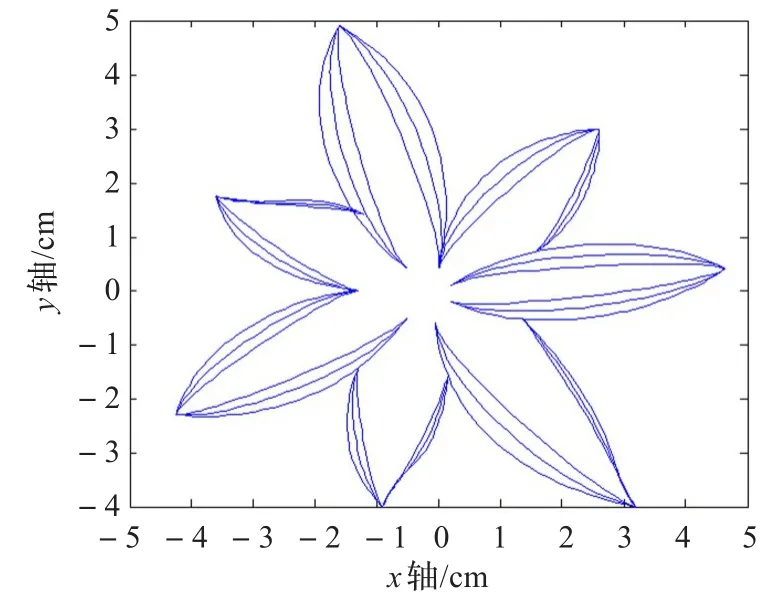
图9 (a) μ=λ时曲线的形状调整
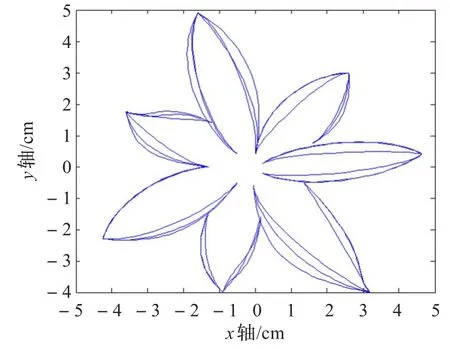
图9 (b) μ≠λ时曲线的形状调整
由于扩展曲线在控制顶点P1和P3处引进调配函数和参数α,因而曲线形状的调整自由度更大,且当α≠0时,曲线与控制多边形的首末边相切,曲线可以插值于首末边的任意点(如图10)。
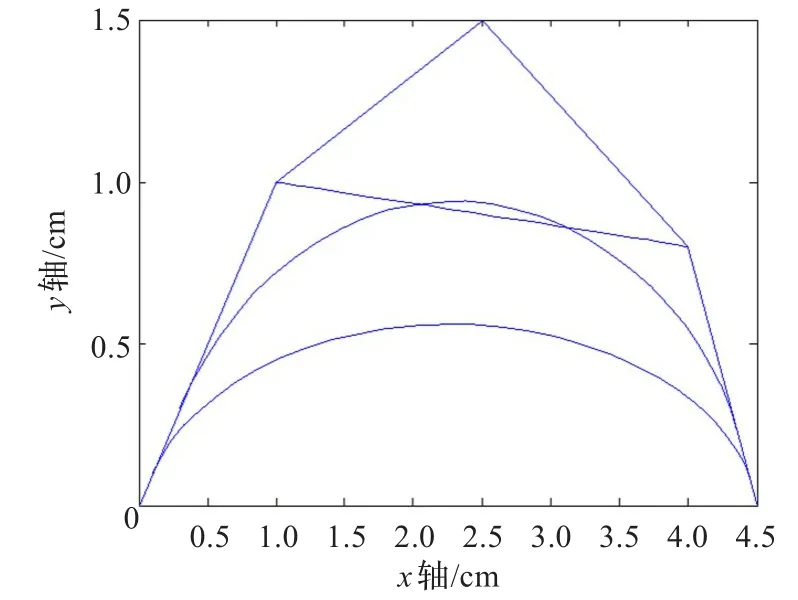
图10 扩展的类四次三角Bézier曲线
注1在式(10)中,当α=1时,即为式(1)定义的带两个形状参数的类四次三角Bézier曲线;当α=0时,为连接P1P3的直线。
2.2 扩展曲线的性质
(1)端点性质
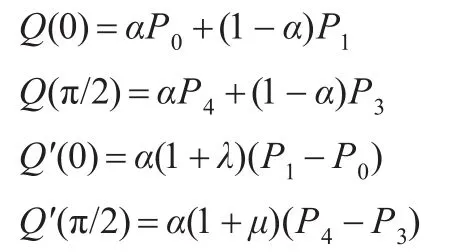
(2)对称性。保持控制顶点的位置不变,只是把它们的次序完全颠倒,那么曲线在下列意义上是对称的:
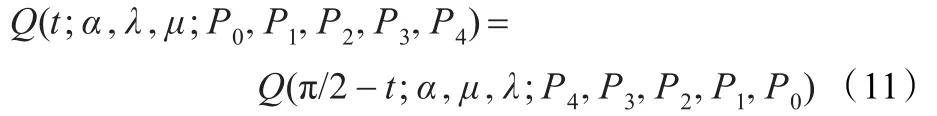
事实上,由调配函数的定义可知:
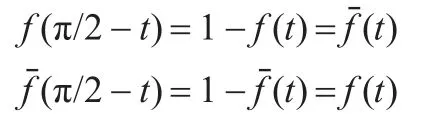
即调配函数具有对称性。于是:
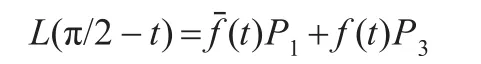
再由带两个形状参数的类四次三角Bézier曲线的对称性,
即知式(11)成立。
下面将Q(t)写成如下形式:

由基函数的性质可得扩展曲线Q(t)的性质:
(3)几何不变性和仿射不变性。曲线形状仅与控制顶点有关而与坐标系的位置和方向无关,即曲线的形状在坐标平移和旋转后不变。
(4)凸包性。由基函数的非负性及权性知,曲线是落在由控制顶点生成的凸包之内的。
(5)局部可调性。曲线具有良好的局部可调性。其中改变α的值可以调整曲线首末点在首末边上的位置。而B(t)的基函数中的两个形状参数λ,μ和α一起,起到对曲线形状调整的作用。
不需改变控制多边形,改变α,λ,μ的取值就可以改变曲线的形状。当α≠0时,其值越小曲线在首末边的切点越接近P1,P3;其值越大曲线在首末边的切点越接近P0,P4。因此曲线与首末边的切点可以由α来控制、调节。如图11(a),λ=1,μ=1,实线的α取值为0.2,“*”线α取值为0.7。
固定α值,调整λ,μ的值,扩展曲线与控制多边形首末边的切点不变,而曲线的形状有所改变。如图11(b),α=0.5,实线λ,μ的取值分别为0.2,0.8,“*”线λ,μ的取值分别为0.7,-0.2。
2.3 扩展曲线的拼接
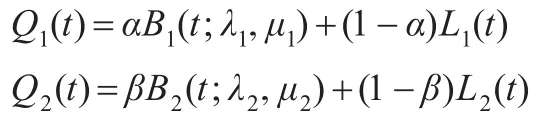
本节讨论两段扩展曲线的拼接问题。设分别为由控制顶点Pi,Qi(i=0,1,2,3,4)定义的两条扩展曲线,其中λi,μi∈[-1,1](i=1,2),0≤α,β≤1。
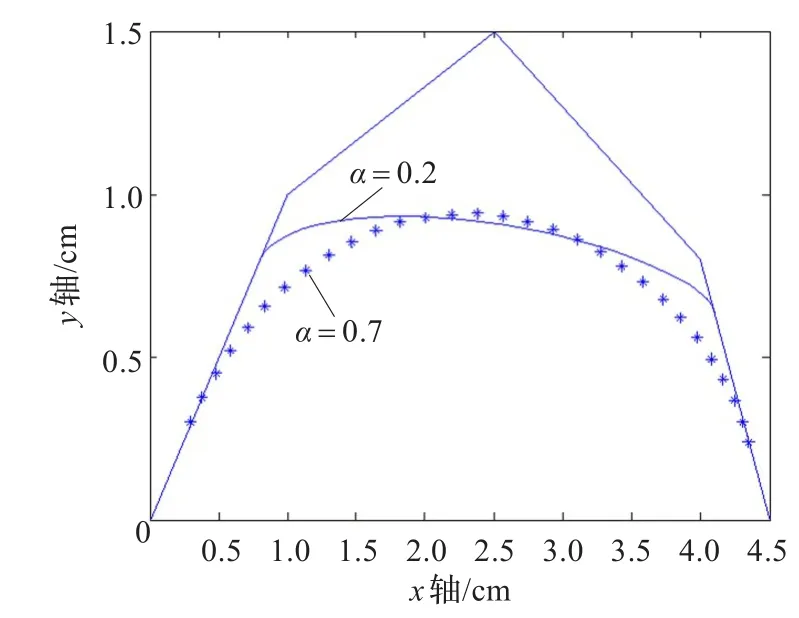
图11 (a) 固定λ,μ值,改变α值对曲线形状的调整效果
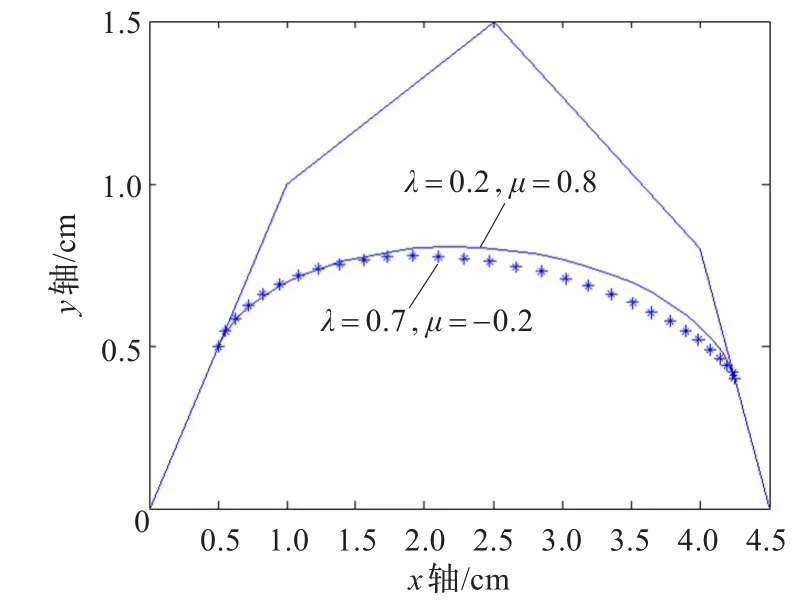
图11 (b) 固定α值,改变λ,μ值对曲线形状的调整效果
定理4扩展曲线Q1(t),Q2(t)达到G1(C1)光滑拼接的充要条件是:

其中ω0=α+βδ2-δ2,ω1=α+βδ2,δ2>0(δ2=α(1+μ1)/β(1+λ2))。
证明要使扩展曲线Q1(t),Q2(t)达到G1光滑拼接,必须满足如下条件:

即满足如下方程组:
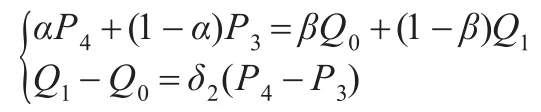
解方程组即得式(13)。
特别,当δ2=α(1+μ1)/β(1+λ2)时,有下式成立:
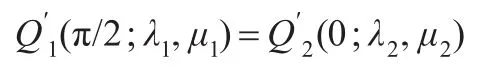
即两曲线在连接点处有公共的切矢,因此两曲线达到C1光滑拼接。
如图12是两段扩展曲线C1光滑拼接的实例。
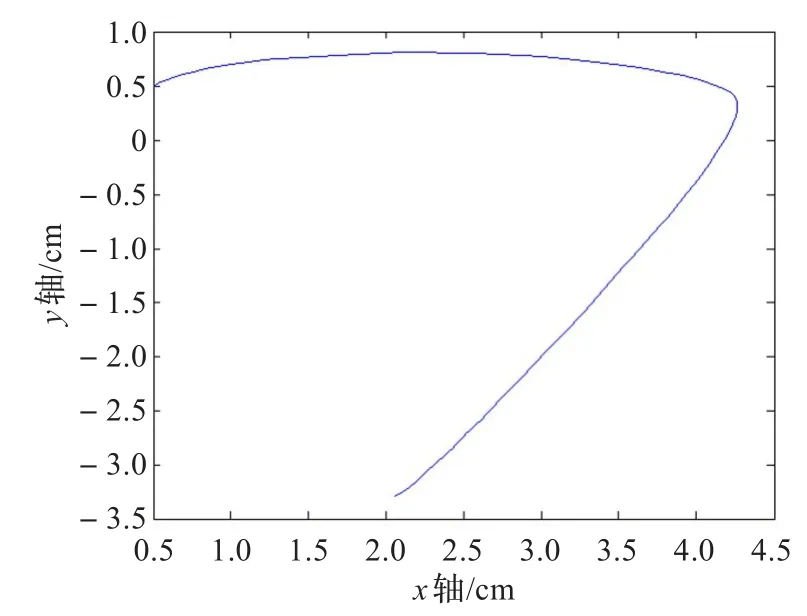
图12 两段扩展曲线的C1光滑拼接
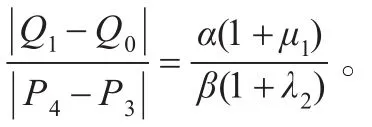
注2当α=β=1时,δ2=δ1,即得定理1的结论。
下面给出两段曲线G2光滑拼接的条件。记P3P4与α[(1-λ1)P0+(2+λ1+μ1)P2-(3+μ1)P3]-2(1-α)(P3-P1)及P3P4与β[(1-μ2)Q4+(2+λ2+μ2)Q2-(3+λ2)Q1]+2(1-β)(Q3-Q1)组成的平行四边形的面积分别为
定理5扩展曲线Q1(t),Q2(t)达到G2光滑拼接的充要条件是除定理4中G1光滑拼接条件外,还必须满足:

其中ρ=β(1+λ2)δ2/α(1+μ1),且P2,Q2在公切线的同一侧。
证明两曲线Q1(t;λ1,μ1),Q2(t;λ2,μ2)在连接点处要达到G2光滑拼接,首先必须达到G1光滑拼接,因此要满足定理4中相应条件;其次在连接点处要有相等的曲率矢。由于两曲线在公共点的曲率为:
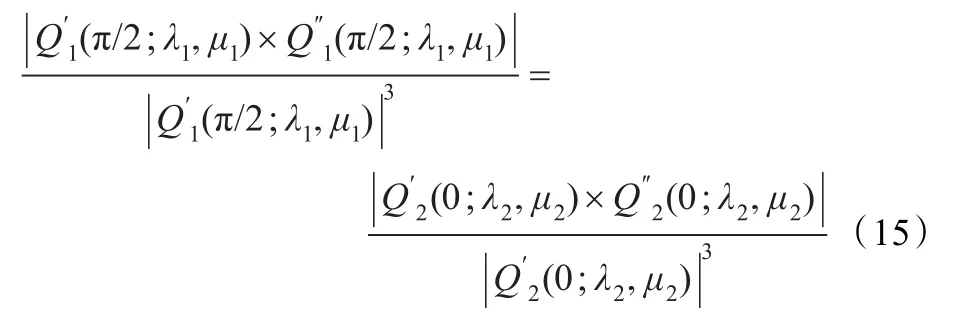
经计算有:
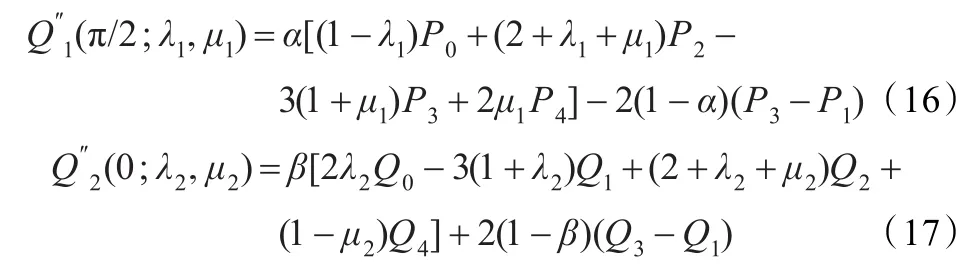
根据扩展曲线的端点性质,并将式(16)、式(17)代入式(15)化简即得式(14)。
注3当α=β=1时,即得定理2的结论。
定理6扩展曲线Q1(t),Q2(t)达到C2光滑拼接的充要条件是除定理4中C1光滑拼接条件外,还必须满足:

其中κ1=β(2+λ2+μ2),κ2=2(1-β),κ3=β(1-μ2),ε0=α(1-λ1),ε1=2(1-α),ε2=α(2+λ1+μ1),ε3=3β(1+λ2)(1-ω1)+2(1-β)· (1-ω1)-2(1-α)-2βλ2(1-ω0)-3α(1+μ1),ε4=2αμ1-2βλ2ω0+ 3β(1+λ2)ω1+2(1-β)ω1,且ω0,ω1,δ2与定理4中C1光滑条件的要求相同。
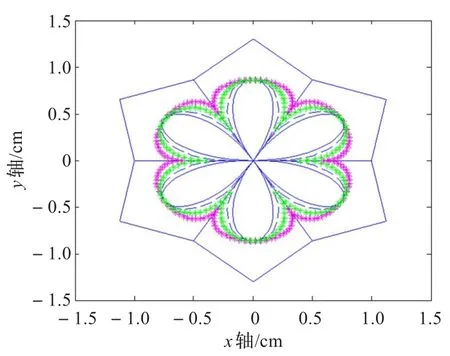
图13 (a)仅修改α值得到的开花瓣
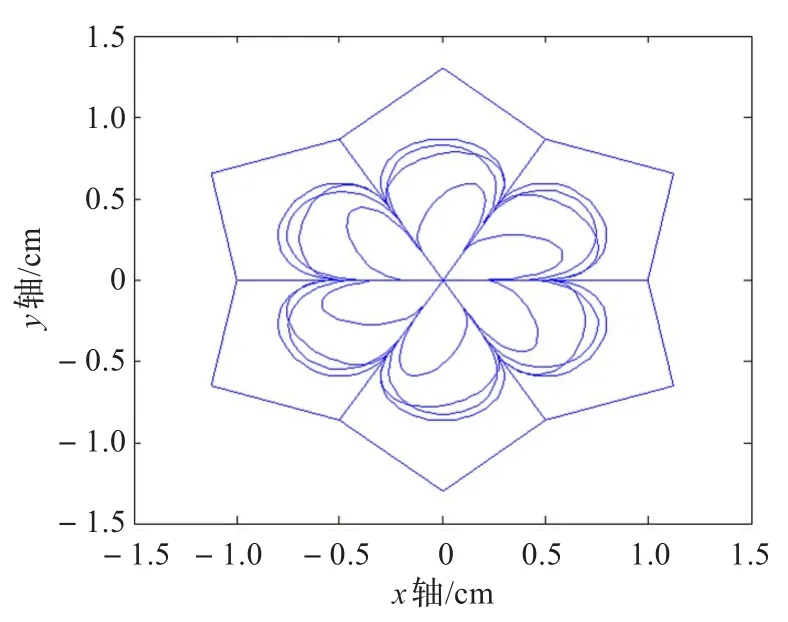
图13 (b)同时修改α,λi,μi得到的不对称开花瓣
证明两曲线Q1(t;λ1,μ1),Q2(t;λ2,μ2)要在连接点处达到C2光滑拼接,首先必须达到C1光滑拼接,因此要满足定理4中相应条件;其次要求二阶导矢相等,即
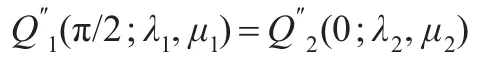
将C1光滑拼接条件及式(16)、式(17)代入上式化简即得式(18)。
注4当α=β=1时,即得定理3的结论。
2.4 扩展曲线的应用
当α=1时,Q(t)即为带两个形状参数的类四次三角Bézier曲线,所以扩展曲线具有该曲线的一切的优点。下面主要讨论扩展曲线在切点修改方面的作用,如图13所示。
由图13可以看出,扩展曲线在不改变控制顶点的情况下,就可以在生成闭花瓣的控制多边形中方便地生成开花瓣。同时还可以通过控制参数α,λ,μ的值来修改开花瓣与控制多边形的切点和形状,生成各种不对称的图形。造型自由灵活。
3 结束语
综上所述,带两个形状参数的类四次三角Bézier曲线不仅保留了原曲线的优良性质,而且其形状可以通过两个形状参数进行调节,因此具有更好的形状可调性和更灵活的逼近方式。该类曲线可以在不改变控制多边形的情况下,生成各种对称和不对称的图形,形状调整简单、灵活,微调能力强;其形状参数几何意义明显:即在给定范围内,λ,μ以不同的方式增大,曲线则以不同的方式逼近控制多边形。该类曲线的扩展曲线不仅具有许多类似于原曲线的优良性质,还可插值于控制多边形的首末边上的任意点:当α=0时,扩展曲线为连接P1P3的直线;当α≠0时,扩展曲线与控制多边形的首末边相切,且通过调整α值可以调整切点在首末边上的位置,因此参数α和λ,μ一起起到对曲线形状调节的作用,曲线形状的调节更加灵活。实例表明,该类曲线及其扩展曲线在非对称图形的造型中具有独特的效果。
[1]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.
[2]Zhang Jiwen.C-curves:an extension of cubic curves[J].Computer Aided Geometric Design,1996,13(3):199-217.
[3]胡钢,秦新强.Bézier曲线的新扩展[J].计算机工程,2008,34(12):64-66.
[4]吴晓勤,韩旭里.三次Bézier曲线的扩展[J].工程图形学学报,2005(6):98-102.
[5]吴晓勤.带形状参数的Bézier曲线[J].中国图象图形学报,2006,11(2):269-274.
[6]Han Xuli.Cubic trigonometric polynomial curves with a shap parameter[J].Computer AidedGeometricDesign,2004,21:535-548.
[7]Han Xian.The cubic trigonometric Bézier curve with two shape parameters[J].Applied Mathematics Letters,2009,22:226-231.
[8]吴晓勤,韩旭里.带形状参数的二次三角Bézier曲线[J].工程图形学学报,2008(1):82-87.
[9]陈素根,黄有度.带多形状参数的双曲Bézier曲线[J].工程图形学学报,2009(1):75-79.
[10]杨炼,李军成.一类带形状参数的类四次三角Bézier曲线[J].计算机工程与科学,2011,33(3):77-81.
[11]刘旭敏,黄厚宽.带形状参数样条曲线的研究[J].计算机研究与发展,2007,44(3):487-496.
[12]王文涛,汪国昭.带形状参数的三角多项式均匀B样条[J].计算机学报,2005,28(7):1192-1198.
[13]王文涛,汪国昭.带形状参数的均匀B样条[J].计算机辅助设计与图形图像学学报,2004,16(6):783-788.
[14]左传桂,汪国昭.具有两个独立形状参数的四阶均匀B样条[J].浙江大学学报:理学版,2007,34(6):622-632.
[15]王文涛,汪国昭.带形状参数的双曲多项式均匀B样条[J].软件学报,2005,16(4):625-633.
[16]李军成,陈国华,杨笃庆.可调的类三次Bézier曲线[J].计算机工程与科学,2010,32(3):69-71.
[17]王成伟.带有切线多边形的一类有理样条的扩展曲线[J].北京服装学院学报,2011,31(1):5-12.
YU Desheng1,XU Yingbo1,ZENG Jiexian2
1.School of Mathematics and Information Sciences,Nanchang Hangkong University,Nanchang 330063,China
2.School of Software,Nanchang Hangkong University,Nanchang 330063,China
A class of quasi-quartic trigonometric polynomial Bézier curves with double parameters and its extension are defined. The properties of the class of the curves and its extension are obtained,and the necessary and sufficient conditions forG1(C1),G2(C2)continuously joining with two segments of quasi-quartic trigonometric polynomial Bézier curves and two extensions are given.The applications of them are discussed.Experimental examples show that the class of the curves and its extensions have stronger abilities in curve designing,especially in designing of non-symmetry figures.
quasi-quartic trigonometric polynomial Bézier curves;shape parameter;extension;continuously joining
给出了一类双参数的类四次三角Bézier曲线及其扩展曲线的定义,得到了该类曲线及其扩展曲线的性质,给出了两段双参数的类四次三角Bézier曲线G1(C1),G2(C2)及两段扩展曲线G1(C1),G2(C2)光滑拼接的充要条件,并讨论了这两类曲线的应用。算例表明,该类曲线及其扩展曲线在曲线造型,特别是在非对称图形的造型中,具有很强的描述能力。
类四次三角Bézier曲线;形状参数;扩展;光滑拼接
A
TP391
10.3778/j.issn.1002-8331.1112-0347
YU Desheng,XU Yingbo,ZENG Jiexian.A class of quasi-quartic trigonometric polynomial Bézier curves with double parameters and its extension.Computer Engineering and Applications,2013,49(18):180-186.
国家自然科学基金(No.61165011)。
喻德生(1959—),男,教授,硕士生导师,研究方向:计算机辅助几何设计;徐迎博(1986—),女,硕士研究生,研究方向:计算机辅助几何设计;曾接贤(1958—),男,教授,主要研究方向为工程图学、图像处理和计算机视觉。
2011-12-19
2012-04-18
1002-8331(2013)18-0180-07
CNKI出版日期:2012-05-22 http://www.cnki.net/kcms/detail/11.2127.TP.20120522.1108.009.html
