卷烟生产计划排产模型建立与优化

2013-08-30祁跃东JINJianJINZhaoQIYuedong

计算机工程与应用 2013年18期

关键词：牌号卷烟遗传算法

金剑，金钊，祁跃东 JIN Jian,JIN Zhao,QIYuedong

1.红塔集团玉溪卷烟厂，云南玉溪 653100

2.云南大学信息学院，昆明 650091

1.Hongta Group Yuxi Cigarette Factory,Yuxi,Yunnan 653100,China

2.School of Information Science,Yunnan University,Kunming 650091,China

1 引言

尽管很多卷烟企业采用了ERP软件的排产调度模块，但核心算法与软件受制于人，卷烟详细排产主要采用人工根据经验进行各卷烟牌号的排产，排产方案的优劣取决于人工经验，ERP的模块更多是作为一种生排程优化功能。随着卷烟“一点控制、多点生产”的协同制造格局快速形成，产品需求小批量、多牌号发展及各种生产工艺约束限制，这种模式影响卷烟生产排产效率和快速反应能力的提高，难以对制造资源进行全面优化配置，妨碍了对生产运作过程的优化[1-3]。

由于生产排程问题本身属于NP难问题，寻求最优解比较困难[3]。卷烟生产排产不仅要处理错综复杂的约束条件，还要从“无穷”多种满足约束的可行方案中找到优化排程方案，这是ERP计划模块面对的真正瓶颈问题，其中的关键在于算法。因此，迫切需要开展卷烟生产排产调度优化技术研究。

图1 卷烟生产流程

卷烟生产包括了离散式模型，如卷包机组排产，主要是解决多机组，多资源的优化调度问题；流程式模型，如制丝线生产，主要是解决顺序优化问题；多点生产组是解决成本优化问题[2-3]。因此需要建立各环节的排产数学模型，开发烟草行业高级计划排程算法，在给定约束：设备资源、生产任务订单、工艺要求、生产成本、运输成本等约束条件下，快速对卷烟生产计划进行优化，实现各种优化目标如：总生产成本最低、库存最少、完工时间最短、换牌次数最少、提高设备运行效率、平衡设备负荷，以达到产能均衡的目的；以实现敏捷制造、精益化生产[4-7]。

2 卷烟生产排产优化流程分析与设计

2.1 卷烟生产简介

香烟的生产是一个复杂的工艺流程，其生产线包括了诸多环节。从工艺上，可以将整个生产线抽象为两个相对独立的环节：制丝和卷接。它们中间存在一个缓存区，即储柜，用来存储半成品烟丝，制丝通过加丝机对卷包进行烟丝供应。生产出的卷烟封箱后存入成品高架库，供销售发货。某生产点基本生产流程如图1所示。

其余各点生产流程基本类似，区别在于卷包设备机型、数量存在差异；同时各生产点生产成本、运输成本存在差异。

2.2 卷烟排产递阶优化流程设计

为适应市场对产品需求的快速变化，根据实际卷烟生产计划业务，采用分层递阶设计相应的优化流程。通过市场定单需求与销售预测，形成月度销售进度计划；根据月度销售计划制定周滚动生产计划，经过优化分解处理为各个生产点生产计划；各生产点利用详细排产模型自动生成生产进度计划。在构建排产模型时，从上至下地考虑各个层次的目标函数和约束条件，较高层次的任务分配模型优化结果作为下一层各生产点的约束。同时，较低层次各生产点的实际生产情况实时反馈给上一层，用以调整上层计划。以此更好地预测和指导生产，响应市场需求。根据上述步骤，把整个生产计划优化模型分成两个层次。详细流程如图2所示。

（1）需求分配模型：根据集团销售计划部门制定的月总生产计划，分解为周滚动计划，考虑各生产点生产能力、生产运输成本、工艺约束，进行成本的优化。对总生产计划进行分解，利用生产点需求分配模型自动将周计划分解为各生产点的任务列表-各牌号的卷烟计划箱数。

（2）各生产点的生产排程模型：根据上一层模型分配到每个生产点的需求计划，考虑各点的设备资源，工艺约束，对卷接环节进行排产，优化出每日生产进度计划，即每天各加丝机上生产某种品牌香烟的箱数，再通过加丝机与间接机组的配置关系，把加丝机任务按机组能力进行分解，得到每个机组的派工单。

制丝环节优化模型：根据卷接环节优化结果和储丝柜调度计划，在满足卷包环节衔接需求的约束下，根据卷烟加丝机计划，对多条制丝线进行批次任务分配、排序优化，给出丝线各工序段的排产工单。

流程需要考虑的方面如下：

（1）为了更好适应市场需求变化，企业需要制定灵敏度更高的生产计划，在月度计划的基础上制定周滚动生产计划，周滚动计划可以根据当前周计划的执行情况和销售需求的变化来修正下周的计划，并逐期向前移动。通过周滚动计划动态编制方法，将销售需求、生产执行反馈随时间的变化纳入到计划的动态调整中，在保留计划应有的严肃性的同时增加了计划的灵活性[2]。

（2）在生产点详细排产中，不同生产点存在不同的卷包机型，其性能工艺要求各不相同，需要保证设备任务负荷的均衡性、生产的连续性，尽快完成订单生产任务，避免拖期损失等。

（3）多点任务分配与各点详细排产衔接：由于成本考虑、工艺要求、质量追溯，卷烟生产采用了批量投产，每台卷接设备必须连续生产一定批量卷烟，才能进行换牌号或结束，也就是按批次生产。因此需要把上层优化后的任务列表进行批次转化，把各牌号的卷烟需求箱数除以投产批量转化为批数，超出计划的部分作为在制品。

（4）生产优化约束：生产计划的约束是多方面的，对卷烟企业来说，制定生产计划时要考虑的制约因素主要包括：周滚动需求计划、生产能力、库存水平、工艺限制。而生产原料、辅料供应，通常不成为制约因素。在进行卷烟生产计划的优化时，必须对各种约束进行考虑，方案必满足各种实际生产限制。

图2 卷烟多点生产排产优化总体流程

3 卷烟生产优化建模

在考虑资源约束时，可以选择各个环节的瓶颈资源作为约束条件，这样就能使整个建模过程得到合理的简化。在构建和求解模型中，对总体流程的多点任务分配和生产点详细排产环节分别建立排产数学模型。

3.1 卷烟多点生产任务分配模型

多点任务分配模型主要是根据对周滚动计划任务进行分解，生成各个生产点生产计划，即已知n个品种香烟在一个周期内的需求计划，现在有m个生产点分别能生产n种香烟中的某些品种，其生产、运输成本各不相同，在满足各生产点生产能力限制的前提下，将总的计划合理分配到各个生产点。根据企业的实际需求，在构建模型时考虑了以下因素：（1）优化目标：使总的生产成本最低、库存最小。（2）约束条件：①各生产点每天的总生产量不能超过该生产点当天的力限制；②任何品种在所有生产点的产量总和，要能满足周期内该品种的需求。用数学语言描述如下：

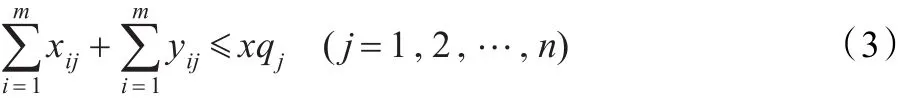
xij生产点i生产品种j香烟的数量，单位：箱。 f(xij)生产点i生产品种j香烟的生产成本函数，若i生产点不能生产品种j，则为∞，单位：元。nli生产点i在周期内的生产能力上限，单位：箱。xqj品种j香烟在周期内的需求量，单位：箱。ci第i个生产点的运输成本系数，单位：元。 yij生产点i品种j的在制品库存，单位：箱。

图3 卷烟生产短期成本函数曲线

四个生产点的产量成本函数 f(xij)，如图3所示，横轴为产量，纵轴为生产成本，即短期总成本随产量变化的关系。曲线的形状取决于生产要素的边际报酬。

由于四个厂的生产设备、工艺、管理水平存在差异，因此成本函数各异；同时各卷烟牌号生产成本系数也各不相同。因此需要根据各个生产点生产不同品种香烟的生产成本函数、卷烟综合运输成本进行优化，同时要考虑牌号生产点的限制。

3.2 加丝机详细排程模型

根据卷烟生产流程，生产点详细排产模式可以描述为：有m台加丝机，要加工n个批次的卷烟。每个批次可以在某些加丝机上生产，用一道工序加工完成；每个牌号卷烟在不同加丝机上的加工时间一定，且各不相同。详细排产目标是把n个批次的卷烟安排到特定时间段、特定机组资源组合上，使最大完工时间最短。该问题在Makespan指标下已被证明是NP完全问题，所有分配方案为mn种[8]。令t(k,i,j)为第k个牌号第i批卷烟在机器 j上的加工时间，假设牌号k的批次i在机器 j上加工，则 x(k，i，j)=1，否则x(k，i，j)=0，则可定义广义加工时间为 x(k，i，j)t(k，i，j)。同时考虑同一台加丝机上加工不同牌号之间的换牌时间和首批准备时间，则机器 j的Makespan指标取决于该机器加工批次的数量、加工时间和换牌次数。为减少换牌次数，同牌号批次在加丝机上连续生产。机器 j上的完工时间为：

其中t(k-1，k，j)为牌号k在机器 j的换牌时间，p为卷烟的牌号数量，ts为机器 j首次生产准备时间，y(k，j)=1表示牌号k在 j上加工。进而整个加工过程的最大完工时间和相应的调度指标分别为：

4 解决方案（两阶段优化）

由于模型目标函数非线性，约束条件多，解空间巨大，经典常规算法不能获得满意的解，因此需要采用智能算法来求解。遗传算法GA是一种模拟生物进化过程的随机搜索算法，将问题的求解表示成一群“染色体”，并将它们置于问题的环境中，根据“适者生存”的原则，从中选择适应环境的“染色体”进行复制，通过交叉、变异等操作产生新一代更适应环境的“染色体”群，通过不断进化，最后收敛到一个最适应环境的个体上，即为问题的最优解。适合于大规模复杂的生产任务分配问题[8-9]。

4.1 多点任务分配遗传混合算法设计

针对多点非线性成本优化问题的特点，业界普遍采用遗传算法进行求解[5-9]，遗传算法具有快速随机的全局搜索能力，能够在短时间内为优化问题提供近优解，且毋需太多的问题域知识，并自然地适合并行实现，其自适应性和自学习性特别适合于求解现实中具有大规模状态空间的优化问题。但其存在迭代停滞的问题，当迭代到一定代次，即达到近优解时往往会做无用的冗余迭代，无法到达最优解。换句话说，遗传算法容易陷入到次优解[10-11]。

因此，单独使用遗传算法难以满足多点非线性成本最优的要求。而模式搜索具有很强的细搜索能力[10-11]，易于发现局部最优解，但是其全局搜索结果的最优性在很大程度上依赖于初始点的选择。遗传算法强于全局近优搜索而弱于局部细搜索，模式搜索强于局部细搜索而弱于选择接近最优的初始点。本文采用遗传算法“投放”模式搜索到近优点，而模式搜索从近优点开始细搜索最优点的想法。提出了一种混合遗传算法-模式搜索的最优化方法：该方法是首先通过GA算法进行全局范围的优化，在此基础上使用局部寻优精度好的模式搜索法。GA进化后得到全局近优个体，模式搜索以此遗传近优个体作为初始值，进行快速局部最优搜索，改善遗传算法局部寻优精度较差的固有缺陷，两种算法取长补短。该算法流程如图4所示。

综合算法的基本步骤是：

图4 GA+PS混合算法流程

（1）设定算法各项控制参数，问题的解显然取决于生产点i生产品种j香烟的数量xij的取值，只要确定了每个基因xij，即由公式（1）计算分配方案的成本性能指标，作为进化搜索的驱动力。直接采用n×m矩阵实数编码表示分配方案，基于矩阵进行算子操作。这种编码解直观、易于操作。随机生成初始分配种群。

（2）根据适应度评价种群。根据式（1）～式（3）计算种群中每种分配的目标函数值和适应度值。

（3）遗传算子操作。通过选择、交叉、变异和替换等操作生成新的种群。

（4）判断条件：满足遗传进化停止条件，从最终的种群中挑出最优解，转到（5），否则转入（2）。

（5）把最优个体作为模式搜索的起始点，进行迭代运算，初始点R0=GA最优解。

（6）根据模式确定搜索方向，计算出网格Rn，计算目标函数 f(Rn)。

（7）对网格进行表决，f(Rn)＜f(R0)网格点的目标函数值小于当前点的函数值，表决成功，该点作为下次迭代的当前点R0=Rn，同时增大网格尺寸。否则当前点保持不变，收缩网格尺寸。

（8）然后继续迭代，判断网格尺寸δ＜ε截止误差容限，如是，则停止搜索。

（9）判断是否再继续遗传算法，如继续，则把模式搜索最优解加入GA种群。

4.2 加丝机详细排产遗传算法策略

针对生产点详细卷烟排产，进行如下转换设置：（1）获取优化后的生产点卷烟生产箱数计划，按卷烟牌号进行批次拆分，得到不同牌号卷烟的对应批次任务；（2）根据卷包机组生产能力及配置关系，计算出加丝机的整体能力；（3）对卷烟牌号的生产机型限制、牌号优先级进行设定。

该并行机器调度问题的GA算法主要策略如下：

（1）编码：问题的解显然取决于 x(k，i，j)的取值，由于矩阵编码涉及的基因太多，存在大量的冗余信息，不便于遗传操作的设计，因此采用自然数编码来解决这个问题。即由n个取值为[1，m]之间整数的基因kj构成染色体[k1k2…kn]，记为X，每个基因代表该批次加工的加丝机号。进而由公式（4）～（6）计算染色体调度方案的Makespan性能。

（2）遗传算子操作：将最大流程时间的倒数作为适应度函数；采用轮盘赌进行选择；采用次序交叉；变异采用翻转变异。为了实现GA算法在保持种群多样性的同时，保证算法的收敛性。在进化后期，采用自适应算法，使交叉与变异随适应度自动改变。

（3）规则约束：由于卷烟生产存在着许多的规则要求和工艺限制，在排产时必须予以考虑：①加工的品牌尽量由高到低，即同一台加丝机上品牌高的优先生产；②某规格必须严格限定在某些加丝机上。因此需要在遗传算法设计中考虑各种规则和限制。首先在编码时对受限的牌号的编码取值范围进行限定，排除不能生产该牌号的加丝机编码；然后在个体解码过程中，对加丝机分配任务进行优先级排序。保证进化操作过程中不出现非法染色体。

5 卷烟排产实例分析

5.1 问题实例

现有8个牌号卷烟牌号在一个周期内的需求量，如表1所示，要将生产任务合理分配到4个生产点进行生产。

表1 卷烟生产需求表箱

表2给出了各生产点不同牌号卷烟的生产成本系数，考虑了人工成本、机器损耗、物料供应成本等在内的综合生产成本系数（注：“--”表示该生产点工艺上不具备生产某品种香烟的能力）；最后一行是生产点的物流运输成本系数/箱。

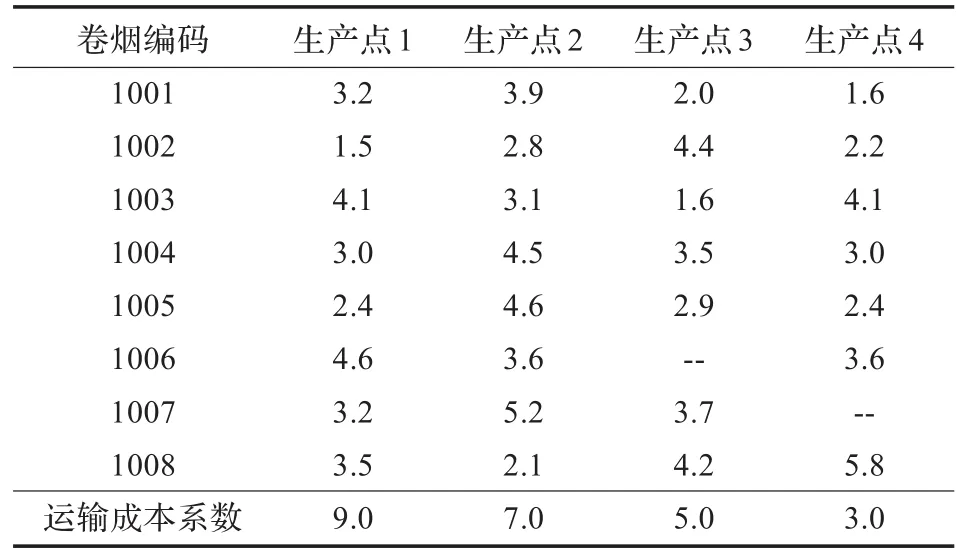
表2 各生产点不同牌号卷烟成本系数

表3给出各个生产点每周期的最大生产能力；表4是各生产点各牌号卷烟的在制品库存。

表3 各个生产点每天的最大生产能力（箱·周－1）

表4 各个生产点在制品数量箱

目标是在满足周需求计划，各点生产能力限制的前提下使总成本最低，在制品库存最少。

生产点详细排产以6个加丝机单元为例，每个加丝机连接不同数量、型号的卷包机，共30台卷包机。目标是确定批次任务在加丝机单元的分配，考虑工艺路径约束，使最大生产流程时间最短。

各牌号卷烟批次不同设备加工时间如表5所示。为方便起见，规定设备不同牌号中途切换时间都相同，为30 min。首个牌号开始生产的准备时间为15 min。

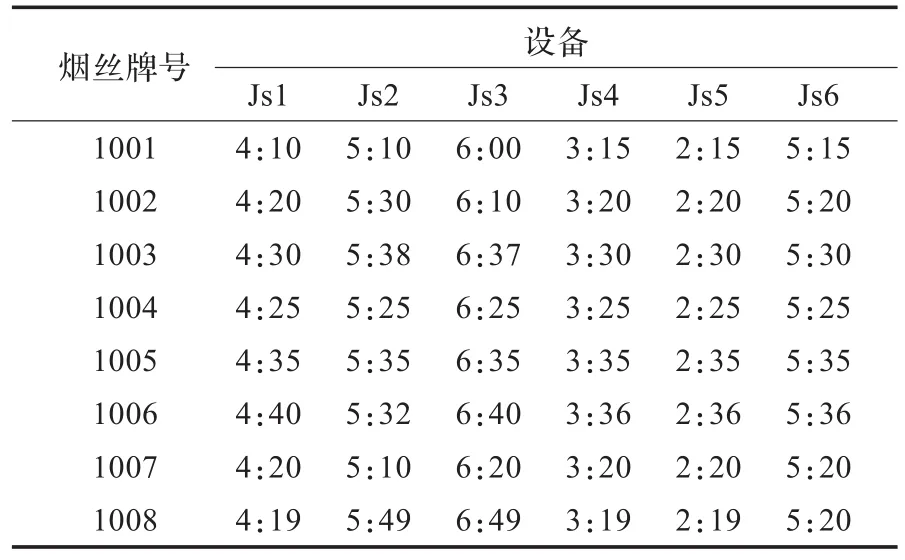
表5 烟丝工序加工时间表（h：mm)

5.2 程序运行结果分析

针对多点任务分配，设置算法参数：模式搜索表决方法采用GPSPositiveBasisNp1模式由N+1个向量组成，最大迭代次数400；遗传算法种群数量30，变异方法为自适应可行变异，交叉为启发式交叉，进化30代无改进则停止。

优化结果见表6，各牌号卷烟生产量加上库存满足了周需求；各点生产总量小于生产能力限制；各点生产的牌号满足了工艺限制。该方案的总生产成本482 986.18，实数编码小数点向上取整。

表6 各生产点一周内的任务计划箱

图5 混合算法进化过程

混合算法进化过程如图5所示，上图为遗传算法最佳适应度进化图；下图为模式搜索最佳目标函数迭代图。当GA进化到150代时收敛、停滞，而模式搜索在此基础上进一步搜索，迭代200代后，得到了更好的成本优化指标，该混合算法改善了在单独使用遗传算法会出现的迭代停滞问题，或在单独使用模式搜索法难以选择搜索初始点的问题。

以生产点2分配的卷烟任务为例，转换成生产批数，共75批各牌号卷烟。可用的加丝机限制如表7所示。

表7 卷烟生产订单表

加丝机上的牌号优先级为（P8、P7、P6、P5、P4、P3、P2、P1）。种群规模m=20；遗传运算的终止进化代数T=20；保留最佳个体。

优化结果如图6所示，图中不同颜色代表不同批次卷烟，该图直观地给出了不同牌号批次卷烟任务在b1～b6加丝机上的分配方案。通过窗口，可以精确地查看每一牌号批次生产任务详细排产信息；同时从图上可以反映出工厂日历对生产的影响，工作日历每天6：00—20：00，下方蓝色块表示生产周期内排班休息时间。这为生产提供了有价值的精确参考。可以看出好的排产方案，使所有设备的工作效率提高，设备负荷均匀，因此如何对各牌号卷烟排产是提高设备总体效率的关键。

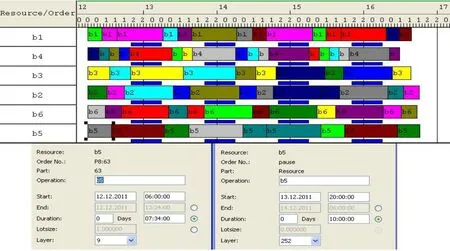
图6 卷烟批次排产甘特图

该算法以较小的时间代价，通过1 380次计算，得到了任务分配方案，获得了近优的满意结果，总完成时间在20代第10个体获得最优值：2 d19 h57 min；优化耗时：1 min15 s，换牌次数：32次，证明了算法的有效性。从图7的进化适应度图谱，可以看出算法收敛性。

6 结束语

针对卷烟多点生产任务分配与单生产点详细排产优化实际问题，提出了一种混合遗传算法和模式搜索的优化模型进行求解。综合遗传算法强于全局求近优的能力，和模式搜索强于局部求最优的能力，有效解决了卷烟排产优化的复杂性，获得优化、可行的排产方案，降低卷烟多点生产成本、缩短生产完工时间。通过改进遗传算法为现有ERP卷烟排产功能的完善提供有益的参考。同时还需要对排产优化算法与ERP系统订单管理模式的集成进行相应的研究，更好地发挥各自相应的作用，为生产资源的优化配置奠定基础。