角接触球轴承的应力场与相对疲劳寿命分析
2013-07-20程超汪久根王爱林洪玉芳
程超,汪久根,王爱林,洪玉芳
(浙江大学 机械工程学系,杭州 310027)
角接触球轴承广泛应用于机床主轴和汽车轮毂单元中,要求有高的耐磨性和较长的疲劳寿命。然而,轴承的耐磨性和疲劳寿命都与钢球与内、外沟道的应力场密切相关。轴承的疲劳裂纹源有表面粗糙峰微小裂纹和零件表层的疲劳导致的裂纹[1],可以通过表面精加工减少或消除;但是在一定应力循环次数后,由于零件表层材料受交变应力作用,会在表层产生裂纹,裂纹扩展后形成疲劳剥落。因此,零件表层应力场的研究就成为长期以来关注的问题[2]。
角接触球轴承的接触问题为椭圆接触。文献[3]提出了椭圆参数和最大正交剪应力的简易计算方法。文献[4]认为接触角随钢球位置角和径向载荷变化。文献[5]提出了用Excel编程计算椭圆接触问题的方法,得到了接触应力,椭圆长、短半轴和弹性趋近量。文献[6]给出了椭圆参数计算的拟合公式,但在主曲率相等时误差较大。文献[7]认为,细化网格和增大计算区域可以提高接触问题的计算精度。文献[8]给出了椭圆接触区方向角的计算公式,用于求解一般椭圆接触问题。文献[9]计入球组寿命,计算了整套深沟球轴承和角接触球轴承的疲劳寿命,并分析了密合度对轴承疲劳寿命的影响。文献[10]分析了真空处理轴承钢的应力寿命指数。文献[2-7]对接触应力的分析已经十分详细,然而轴承的疲劳寿命与应力场之间关系的分析仍沿用Hertz理论,这方面有待进一步的详细分析。另一方面,轴承零件的加工误差对轴承寿命的影响也有待研究。
轴承的球径误差和接触角、沟道曲率半径等几何参数对接触应力场有影响,文中拟研究角接触球轴承的Mises应力场,分析球径变化、沟曲率半径系数和接触角对接触应力场的影响,进而得到其对滚动轴承疲劳寿命的影响。
1 弹性接触的计算模型
将钢球与沟道作为两个弹性体,施加径向载荷Fr后产生弹性变形,形成椭圆接触区域Ω。定义δ为两个弹性体之间产生的弹性趋近量,则
ω1+ω2+f1+f2=δ,
(1)
式中:ω1,ω2分别为钢球和沟道在接触点产生的弹性变形;f1,f2分别为钢球和沟道表面在加载载荷前距名义接触点切线的垂直距离。ω1,ω2可由弹性力学中的Boussinesg公式求得
(2)
式中:E1,E2分别为钢球和套圈的弹性模量;ν1,ν2分别为钢球和套圈的泊松比;s,t为接触区域Ω中点的坐标;p(s,t)为径向载荷作用下分布在接触区域Ω上的接触应力。
同时,根据平衡条件,表面应力分布沿接触区域的积分应与所作用的总载荷相等,即
(3)
(1)~(3)式组成了角接触球轴承钢球与沟道接触问题的基本方程。计算中将接触区域划分为多个单元,在每个单元格上假定接触应力为定值,然后将(1)、(3)式离散成一个线性方程组,通过求解方程组求得每个单元格上的接触应力。

(4)
钢球与沟道在接触点的弹性变形经离散化后可以写为
(5)
轴承的接触疲劳是裂纹发生和扩展的结果。裂纹可能先从表面下某一深度产生,继而扩展到表面,裂纹的产生和扩展,除了与物体表面或内部的材料缺陷有关外,主要受零件表层内的应力分布影响。要分析角接触球轴承的疲劳机理和寿命,就需要分析接触表面下的Mises应力场。在上述计算获得接触应力p(s,t),并取钢球与沟道的摩擦因数为0.08后,可得到切向摩擦力F(s,t)分布,然后用文献[11]的方法计算出零件表层的Mises应力场。轴承的疲劳寿命与其内、外沟道和钢球的寿命存在以下关系[9]
(6)
式中:Lir,Ler分别为内、外沟道的疲劳寿命;e为系数,对于点接触,e=10/9。
接触表面下平行于滚动方向的最大Mises应力决定疲劳裂纹的发生,应力循环次数越大和受应力体积越小,则材料疲劳破坏的概率越大。Ioannides和Harris疲劳寿命计算模型可表示为[12]
(7)
式中:σM为最大Mises应力;z0为最大Mises应力所在深度;N为应力循环次数,以百万次计;V为受应力体积;c,h为待定指数,对于点接触,c=31/3,h=7/3。应力循环次数可表示为
N∝uL,
(8)
式中:u为轴承转动一周的应力循环次数;L为以百万转为单位的寿命。在获得接触表面下的Mises应力分布后,可根据(6)~(8)式计算出轴承的相对疲劳寿命。
2 分析结果
这里采用的为7010C角接触球轴承,材料为GCr15钢,轴承具体参数为:外径D=80 mm;内径d=50 mm;球组节圆直径Dpw=65 mm;球径Dw=8.73 mm;接触角α0=15°;内沟道曲率半径系数fi=0.52;外沟道曲率半径系数fe=0.52。取钢球与沟道的接触载荷F=200 N,并设定轴承内圈旋转,外圈固定。根据以上参数计算得到的钢球与内、外沟道的接触应力分布呈半椭球体状,接触应力的最大值p0=1.348 GPa。
计算得到的零件表层Mises应力分布如图1和图2所示。沿轴承周向上,最大Mises应力为0.413 GPa,约为0.31p0,距接触表面的深度为79.7 μm,此处即为疲劳裂纹的扩展源。在摩擦力的作用下,接触区内的最大Mises应力位置偏离接触中心线,如图2所示。

图1 沿轴承轴向的Mises应力场
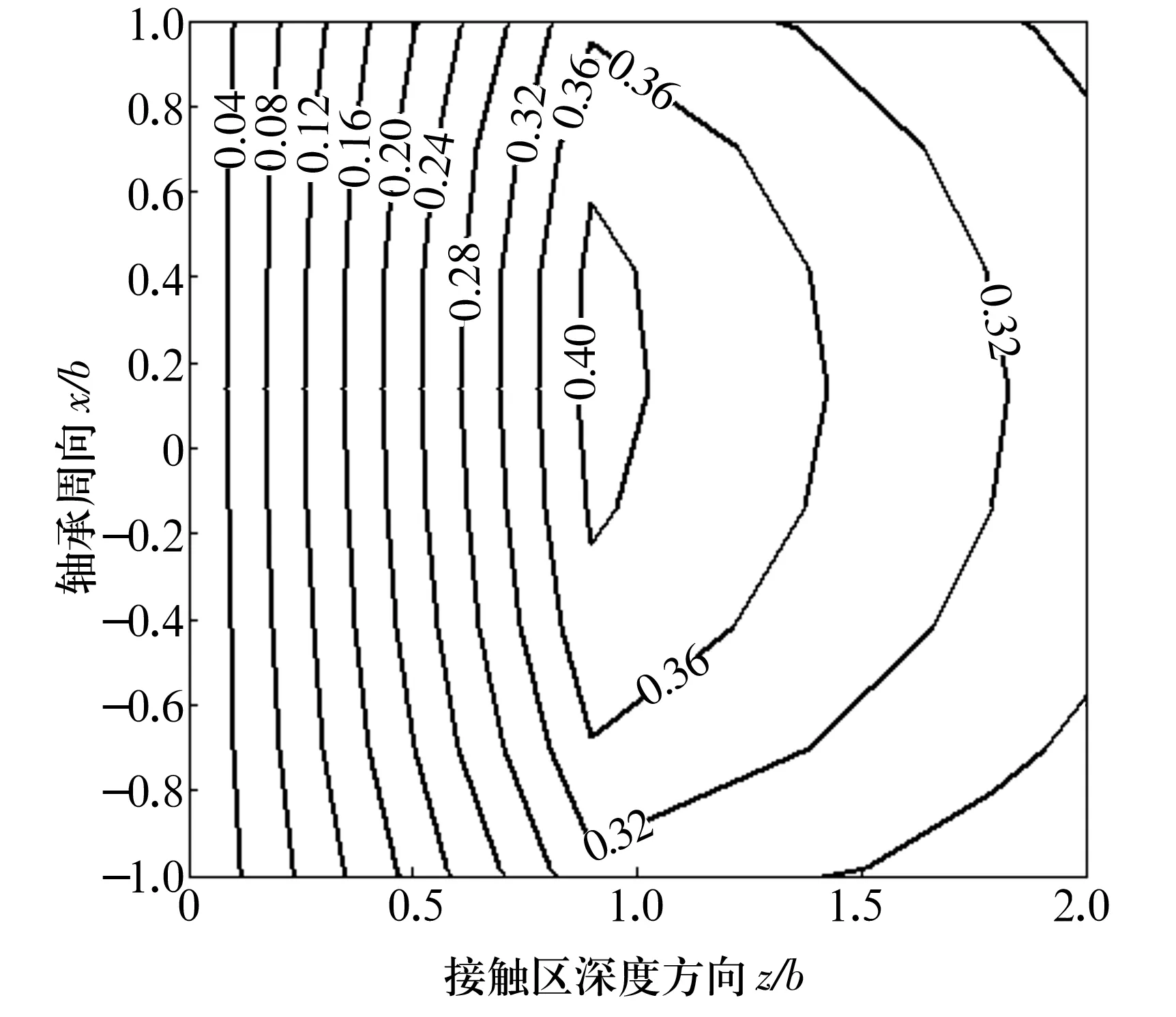
图2 沿轴承周向的Mises应力场
2.1 球径变化的影响
钢球制造过程中,每批钢球之间的直径存在变化。钢球直径的改变对Mises应力会产生影响。取钢球直径变化范围为-1%~1%,其他参数不变,计算Mises应力,结果如图3所示。从图中可以看出,随着钢球直径的增大,最大Mises应力值减小,而最大Mises应力值所处的深度值增大;在轴承周向平面内的最大Mises应力值始终大于轴向平面内的值,说明疲劳首先发生在轴承周向上。钢球直径变化会对接触椭圆面积的大小产生影响,也会使接触应力分布发生变化,这些都会影响到最大Mises应力的深度值。以公称球径的寿命为基准进行对比,结果如图4所示。从图4中可以看出,轴承疲劳寿命随着钢球直径的增大而提高。

图3 球径变化对Mises应力的影响

图4 球径变化对轴承疲劳寿命的影响
2.2 沟曲率半径系数的影响
考虑内沟道曲率半径系数fi的影响时,设定外沟道曲率半径系数fe=0.520,fi的变化范围为0.510~0.530,如图5所示。考虑fe的影响时,设定fi=0.520,fe的变化范围为0.510~0.530,如图6所示。最大Mises应力随沟曲率半径系数的增大而增大;而其深度值却随沟曲率半径系数的增大而减小,即疲劳扩展源的深度变小。

图5 轴承周向上fi的影响曲线

图6 轴承周向上fe的影响曲线
同样的,以轴承周向上的最大Mises应力进行寿命计算,并与内、外沟曲率半径系数为0.52时的寿命进行对比,如图7所示。从图中可以看出,轴承疲劳寿命随着沟曲率半径系数的增大而减小,且内沟道曲率半径系数fi对轴承疲劳寿命的影响比外沟道曲率半径系数fe的影响要显著得多。
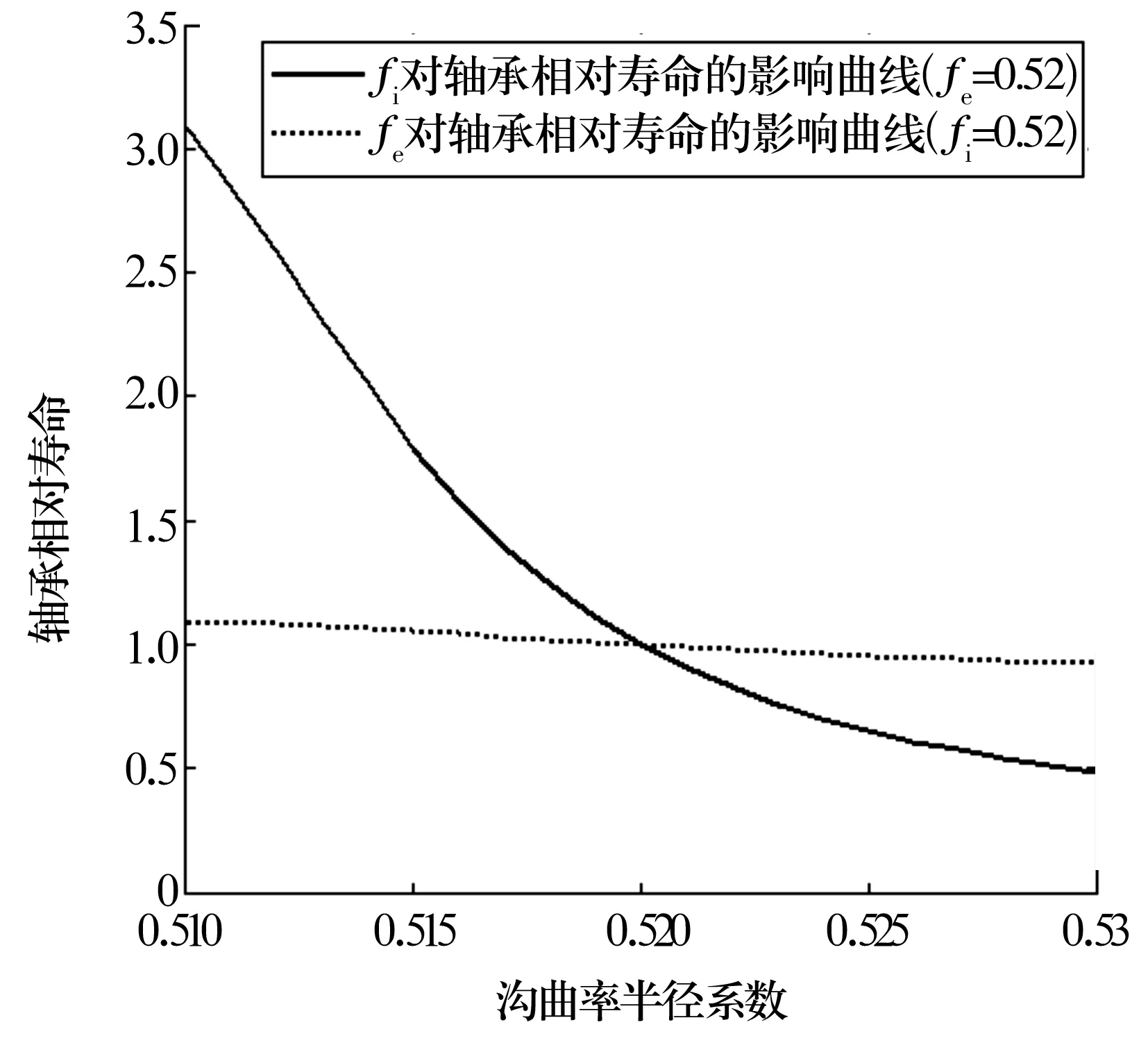
图7 沟曲率半径系数对轴承疲劳寿命的影响曲线
2.3 径向游隙的影响
选取0组(标准组)、1组和2组径向游隙,分析其对最大Mises应力及轴承寿命的影响,结果如图8~图10所示。由图可知,最大Mises应力随径向游隙的增大而减小,其深度值在径向游隙增大时基本保持不变。径向游隙对轴承寿命的影响曲线如图11所示。从图11可以看出,轴承疲劳寿命随径向游隙的增大而减小,但受径向游隙的影响较小。

图8 0组游隙的影响曲线
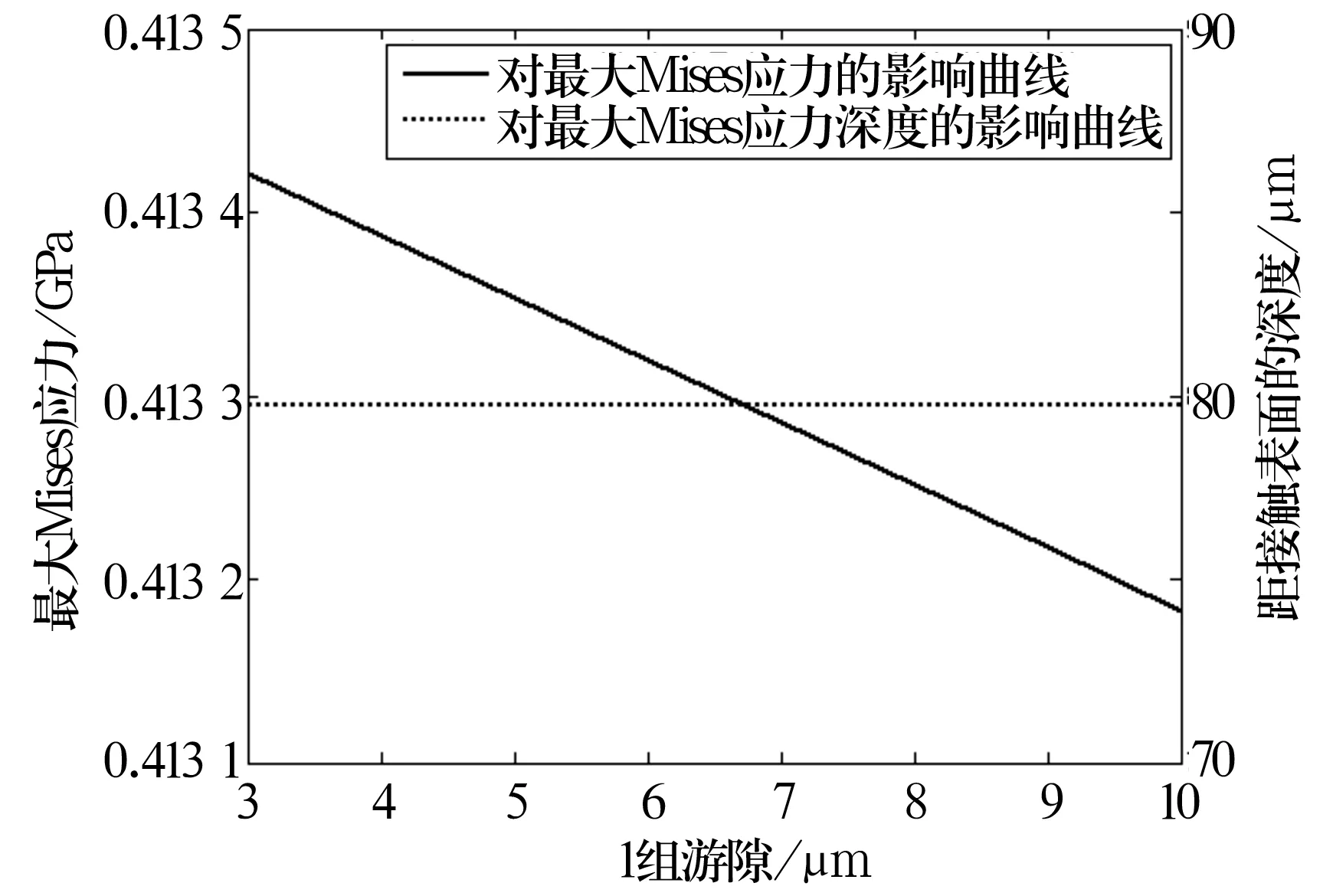
图9 1组游隙的影响曲线

图10 2组游隙的影响曲线

图11 径向游隙对轴承寿命的影响曲线
3 结论
(1)零件表层内Mises应力的最大值总是出现在轴承周向上,即表层疲劳源出现在轴承周向中间面内。
(2)轴承疲劳寿命随着球径的增大而增大,随沟曲率半径系数和径向游隙的增大而减小。
(3)球径、沟曲率半径系数和径向游隙对轴承疲劳寿命的影响程度是不相同的;内沟道曲率半径系数和球径的变化对轴承疲劳寿命影响较大,而外沟道曲率半径系数和径向游隙对轴承疲劳寿命的影响较小。
