FIR 数字滤波器设计及FPGA 实现*
2013-07-20谭家杰
谭家杰
(衡阳师范学院物理与电子信息科学系,衡阳 421008)
1 引言
数字滤波器按照其结构分成无限脉冲响应型(IIR,Infinite Impulse Response)和有限脉冲响应型(FIR,Finite Impusle Response)。有限脉冲响应型的设计方法有窗函数法、频率采样法及其它方法。数字滤波器实现方式主要有以下方法:①直接用DSP(Digital Signal Processor)硬件实现设计的数字滤波器[1-4]。②用 FPGA (Field Programmable Gate Array)器件实现[5-8]。③通用计算机或单片机实现[5,9]。其中,实现方式①②速度较快,因而应用较广泛,方式③受限制,通用机一般用于设计滤波器,单片机则实现一些特殊的数字滤波器。一般的设计方法是采用Matlab 软件[2-3,6,10-11]或面向对象软件[12-14],根据给定的滤波器参数选用相应方法设计出数字滤波器,并检查其幅频特性、相频特性是否符合设计要求。上述方法各有其特点,互有优劣。采用Visual Basic6.0 软件研制出FIR 滤波器设计的计算机辅助软件,是可将滤波器的系数保存并输出为VHDL(Very-High-Speed Circuit Hardware Description Language)语言的数字滤波器程序,经QuartusII6.0 综合产生可在线综合、配置,能实现FIR 滤波器的在线设计、实现及修改。
2 FIR 滤波器设计
2.1 设计原理
FIR 数字滤波器相对于IIR 滤波器具有良好的线性相位,缺点是相对IIR 有较高的阶数。一般的设计原理采用加窗函数方法。首先按照相应步骤设计,得到数字滤波器的系数;然后验证所设计的滤波器是否符合预先指定的指标;最后,根据系统的输入、输出信号以及滤波器的单位冲激响应可以给出滤波器的结构,并用DSP 硬件实现,用C 语言描述,也可以用FPGA 器件实现,采用VHDL 语言建模设计程序[5-6]。用Visual Basic6.0 软件平台按照FIR滤波器原理设计出FIR 滤波器设计软件,并导出实现滤波器的VHDL 程序代码,最后用FPGA 开发软件实现滤波器,从而完成FIR 数字滤波器设计、实现。
2.2 设计软件的界面
用Visual Basic6.0 完成FIR 滤波器的设计,设计方法用加窗法,窗函数有:矩形窗、三角窗、汉明窗、汉宁窗、布莱克曼窗和凯塞窗。其设计的界面如图1 所示。
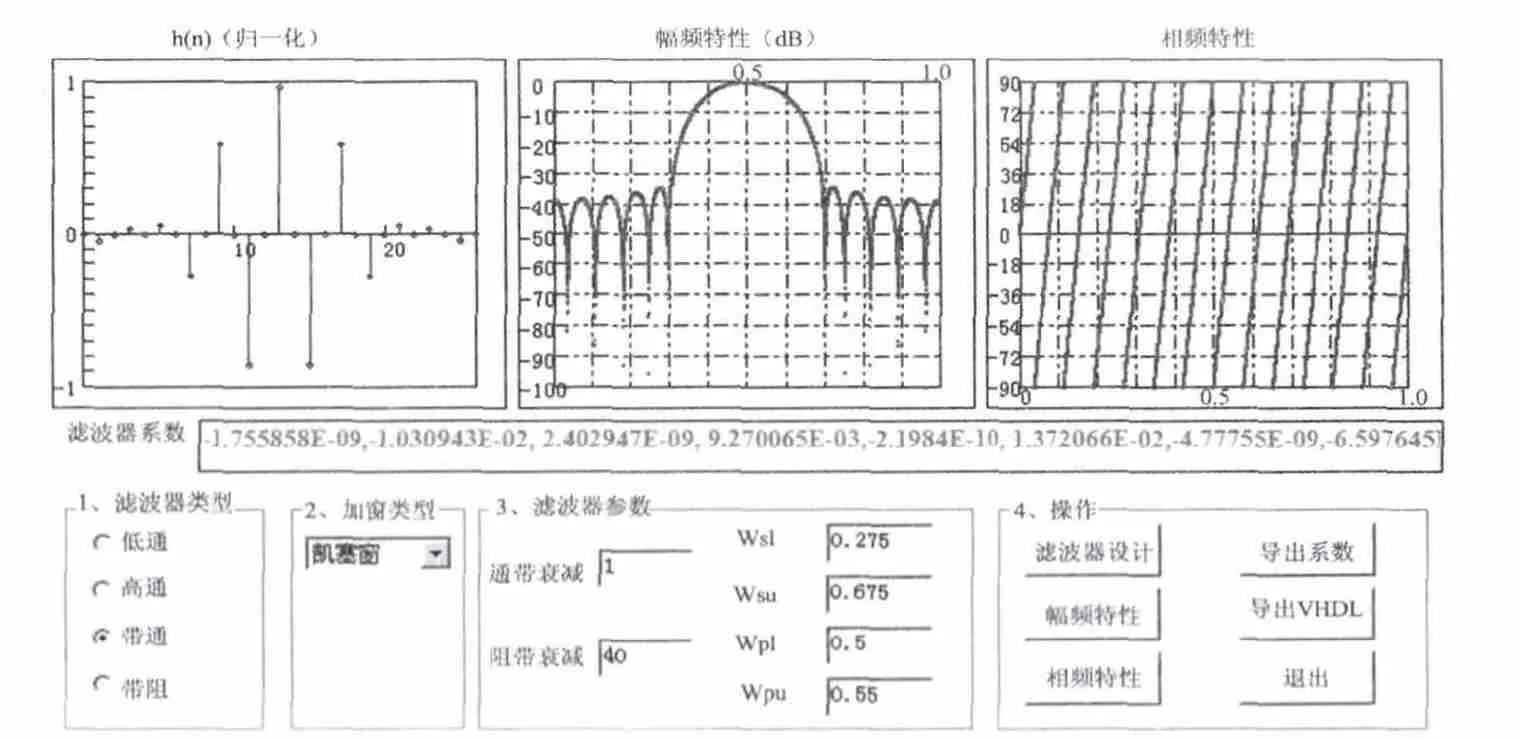
图1 FIR 滤波器设计界面
选择滤波器类型包括低通、高通、带通、带阻四种,这里用四个单选钮,其功能是用于选择滤波器的类型。加窗类型则采用组合框用于运行时选择设计滤波器的六种加窗类型。
设置滤波器参数则采用六个文本框分别用于输入通带衰减、阻带衰减,阻带下边界频率、阻带上边界频率、通带下边界频率、通带上边界频率。其中,采用滤波器类型为低通或高通滤波器时,下面两个输入文本框控件设置为不可见,上面两个文本框控件分别用于设计低通、高通滤波器时输入通带频率和阻带频率。
滤波器设计操作主要由六个按钮组成,实现的功能分别是设计滤波器、查看幅频特性、查看相频特性、导出滤波器系数、导出VHDL 文件及退出。通过前面介绍的控件设置滤波器类型、加窗类型及滤波器参数设计后,只有滤波器设计按钮和退出按钮是可操作的。单击滤波器设计按钮后,幅频特性、导出滤波器系数、导出VHDL 程序按钮变为可操作,此时可以单击上述按钮完成相应操作。但是滤波器操作禁止,因此变为灰色,以防止重复操作导致导出系数和VHDL 程序输出的系数错误。单击幅频特性后,相频特性则为可操作。当单击导出滤波器系数、导出VHDL 程序后,所有按钮除退出可操作外,其余都不可操作,只有重新选择滤波器类型或加窗类型或滤波器参数,滤波器设计按钮才变成可操作。导出滤波器系数是将所有计算出来的系数经过量化程序产生适合于FPGA 运行的数据,不同于界面所显示的。导出VHDL 代码的功能是直接产生可供QuartusII6.0 软件综合的代码,经编译后可以直接配置到芯片中,从而达到在线修改滤波器的目的。
2.3 设计实例
为验证设计软件运行是否正确,给出了两个实例,并将设计的滤波器分别与matlab 设计的滤波器进行对比。
例1 用凯塞窗设计一个通带截止频率0.3π,阻带截止频率为0.5π,阻带衰减为40dB的低通滤波器。
按照例1的要求设置参数,运行设计软件的结果如图2 所示。为了将设计结果与matlab 软件设计对比,分别将两种设计方法设计的滤波器系数用表1 列出。滤波器的长度为23 且为对称,因此表1列出前12个滤波器系数。表1 数据表明设计软件与matlab 软件设计的滤波器系数h(11)相差的最大误差为-0.0004,其余相差很小。采用16 位二进制量化,系数量化最大误差为-26;8 位量化系数误差为-1,采用8 位量化值误差可以不予考虑。说明设计软件在算法及程序设计方面是正确的。
例2 用布莱克曼窗设计一个带阻FIR 滤波器,通带下截止频率为0.2π,阻带下截止频率为0.35π,通带上截止频率为0.8π,阻带上截止频率为0.65π,阻带最小衰减为-60dB,通带最大衰减为1dB。

图2 凯塞窗设计低通FIR 滤波器

表1 设计FIR 系数与matlab 设计对比

图3 布莱克曼窗设计高通滤波器
设计软件得到如图3的结果,设计的滤波器长度为61,matlab 软件设计的结果如图4 所示。对两个图的幅频特性进行对比后可知在通带衰减方面相差不大,主要在阻带衰减方面,matlab 设计的滤波器衰减大近30dB。由于篇幅有限,其它设计就不一一列出。经过仿真实验证明,本设计软件在设计思路、代码编写方面都是正确的,因而采用设计软件设计的数字滤波器是可靠的。
3 FIR 滤波器实现
3.1 FPGA 滤波器原理
FPGA 数字滤波器的实现是以计算机为平台,以FPGA 开发软件QuartusII6.0为工具,以FPGA 芯片为目标器件。由设计软件先设计FIR 滤波器,然后导出实现的VHDL 程序来实现。数字滤波器实现的实质是输入信号与数字滤波器的系数做卷积过程,可用式(1)实现[5]。
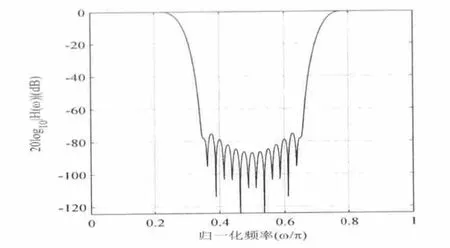
图4 matlab 设计布莱克曼窗FIR 滤波器幅频特性
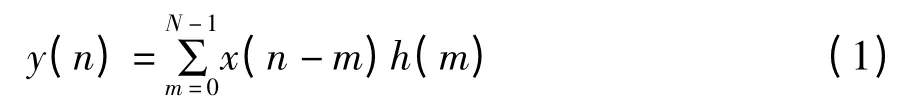
其中x(n)为输入信号,y(n)为输出信号,h(n)为滤波器系数,是设计软件得到的。由于FIR 滤波器的阶数较高,为保证其具有线性相位,其结构具有对称性,因而将式(1)变为式(2)。
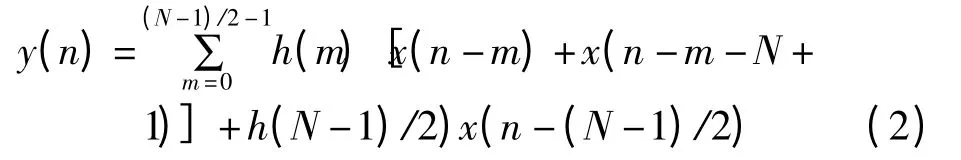
在设计算法时充分利用这点来节约资源,因此只需用滤波器系数的一半完成实现工作。
3.2 FPGA 滤波器实现
从滤波器的结构可知FPGA 实现方法主要有:串行方式和并行方式。串行方式是以牺牲时间为代价,但是其资源的利用率较高。而并行结构则是以消耗大量资源来换取时间的。设计软件采用串行实现,将问题归结为下述主要环节:①滤波器系数的量化问题。②移位寄存器实现。③加法器、乘法器。
FPGA 滤波器系数量化是将设计的浮点系数转换成可供FPGA 实现的数据的过程。量化数据类型有:传统定点数、非传统定点数和浮点数形式。定点数包括无符号整数、有符号整数、二进制补码、二进制反码、正则有符号数字系统(CSD,Canonic Signed Digit)。浮点数相对于定点数来说能在很大范围提供足够的精度,而定点数缺乏这方面的优势,但是定点数在运行速度和解决问题的复杂性方面更有优势。基于上述原因,在量化时必须考虑哪种类型数据更加适合系统的运算方式。设计软件采用传统的整数进行系数量化,既简化了设计软件算法程序的复杂度,又给实现带来方便。VHDL 程序中采用std_logic_vector 数据来实现整型数据,并且开发环境有函数进行转换,如conv_integer 函数,易于程序实现。量化时采用定点整型数据。
移位寄存器的任务是将外部经A/D 转换输入的数据,依次输入与滤波器的系数相乘,需在统一时钟信号和使能信号的作用下完成数据的移位并保存。根据上述原理,设置若干个signal 暂存信号,其数据类型与滤波器数据类型一致,且数据宽度相同,用于将输入信号移位后存储。暂存信号的个数与滤波器系数相同。再设计一个进程起移位寄存器的作用,这个进程的敏感信号为时钟和复位信号。这样的方法有利于Visual Basic 编程实现。
乘法器是数字滤波器实现的关键,根据VHDL 代码并行性的特点,单独设计乘法器模块以供调用。乘法器模块采用移位相加实现,其原理是通过将中间暂存数据进行移位,然后相加实现。而设计软件根据FIR 滤波器长度由公式(2)生成语句完成乘积运算。加法器采用二进制加法运算。加法器、乘法器和移位寄存器在控制模块的统一作用下依次完成。
3.3 QuartusII 仿真
为了对导出的FIR 滤波器VHDL 文件进行仿真,先设计一个加矩形窗的FIR 低通滤波器,阻带衰减为40dB,通带截止频率为0.3π,阻带截止频率为0.4π。设计得到滤波器长度为11的低通滤波器。将设计软件导出的VHDL 文件在QuartusII 6.0平台上进行编译、综合。然后研究QuartusII6.0 综合的滤波器是否满足要求,输入滤波器信号为:

进行仿真时,输入信号量化为整型数据。取一序列{126,-8,71,-56,-31,-62,-70,18,-31,111,0,111,-31,18,-70,-63}设置为输入信号,建立Waveform 文件,仿真得到仿真数据。仿真输出信号为{0,- 6048,- 4656,4472,23686,38574,36837,17293,-13864,-35579,-44127,-35670,- 13363,13808,36214,44406,36262,12360,-17351,-32835,-32583,-15591,-1844,5880,3024,0}。由于不知道输出是否将高频部分信号滤除,因此用Matlab 软件验证。具体做法是将输入信号做256 点的FFT 运算,然后将输出信号也做256点的FFT,得到如图5的仿真信号。
图5(a)为输入信号的频谱,其成分有归一化频率为0.1的低频和0.45的高频,图5(b)是输入信号通过滤波器后,仅剩下低频部分。这个结果说明,设计软件导出的VHDL 文件是正确的。
4 结束语
采用Visual Basic6.0 设计出了FIR 数字滤波器的设计软件,设计软件设计的滤波器正确可靠。该设计方法不同于以往,其创新在于能直接导出VHDL 文件供QuartusII 6.0 综合、配置,从而实现了滤波器的在线设计、在线修改。经QuartusII 6.0 仿真、配置测试,证明这种方法是正确可行的。

图5 滤波器效果对比图
[1]杨达亮,王巨丰.基于DSP的IIR 数字滤波器的设计与实现[J].电子技术应用,2006(11):116-120.
[2]陆广平,卜迎春.基于DSP的FIR 数字滤波器的研究与实现[J].工业控制计算机,2010,23(12):102-103.
[3]邓婷.基于Matlab 和DSP 数字滤波器的设计与实现[J].科学技术与工程,2011,11(19):4597-4601.
[4]梅志红,杨万铨,邓文华.基于快速原型的数字滤波器的设计和实现[J].计算机仿真,2005,22(2):106-109.
[5]孔阳,武杰,万娟,等.基于FPGA 和MCU的低成本地震信号数字滤波器设计[J].核电子学与探测技术,2012,32(1):54-58.
[6]张书召,彭杰.基于FPGA的IIR 数字滤波器的设计与实现[J].工业控制计算机,2010,23(1):105-106.
[7]周戈,曾智.改进的遗传算法在数字滤波器优化应用研究[J].计算机仿真,2011,28(12):215-218.
[8]李姮,田克纯.一种基于FPGA的分布式FIR 数字滤波器设计[J].电声技术,2012,36(10):29-32.
[9]海玉,陈军,钱献芬.一种单片机数据采集系统的数字滤波器设计[J].信息技术,2012(9):175-177.
[10]张大为,姜静,刘迪.基于FPGA的IIR 低通数字滤波器的设计[J].船电技术,2012,32(2):24-26.
[11]俞兴明,周燕.基于DSP的在线FIR 数字滤波器设计及实现[J].国外电子测量技术,2010,29 (5):52-55.
[12]谭家杰,陈淑芳,张兰英,等.基于Visual Basic6.0IIR数字滤波器设计[J].四川理工学院学报(自然科学版),2008,21(2):88-91.
[13]王斌.基于Visual DSP++的无限脉冲响应数字滤波器(IIR)设计[J].电子元器件应用,2012,14(3):36-37.
[14]杨柳,喻金科,张帆.基于delphi的数字滤波器的设计与实现[J].南昌航空大学学报(自然科学版),2007,21(3):50-53.
