一种基于小波变换的MQAM 信号调制识别方法

向培胜，曾 鑫，张 伟

(1.中国人民解放军驻重庆气体压缩机厂军代室，重庆 400030;2.重庆金美通信有限责任公司，重庆 400030)

1 引言

调制样式识别是非合作通信信号分析领域里的一个重要组成部分，它广泛应用于电子对抗、无线电资源管理、频谱监测等领域。在过去的数十年中，调制样式识别技术一直是非合作通信的核心研究内容之一，人们提出了多种自动调制识别算法，然而这些识别算法大都局限于模拟调制(AM/FM/DSB/SSB)或者简单的数字调制(ASK/FSK)。QAM 调制信号以其高频带利用率已经成为宽带无线通信、有线电视、卫星通信等现代通信的主要调制手段，实现这类信号的调制识别是非常必要的。

由于MQAM 信号的复杂度随着调制阶数增加而大幅度提高，增加了调制识别的难度。现有MQAM 调制识别算法主要有基于星座图的数字调制方式识别算法［1－2］，基于似然比方法的调制方式识别算法［3］等。但大多数的算法通常以较高的信噪比为前提，或者需要一定的先验知识(如载频、波特率参数)［4］，在低信噪比时特征模糊，识别效果差，没有对特征抽取的一般化方法。针对MQAM 调制识别在低信噪比下的应用，提出一种基于小波变换和差分运算的MQAM 识别算法。

2 MQAM 信号的小波域特征分析

小波变换是80年代后期发展起来的应用数学分支，近年来基于小波变换的多分辨率特征分析、调制参数估计和调制识别研究方兴未艾。小波变换克服了傅立叶变换时间和频率分辨率无法兼顾的缺陷，在时域和频域同时具有优良的局部化特性，尤其适用于对非平稳信号和突变信号的分析，它可以局部检测信号的奇异性。对于高阶QAM 信号而言，在码元状态变化的时刻，会出现信号相位、频率和幅度变化的奇异点，利用小波变换可对这些奇异点进行检测、分析，从而获得这些点的跳变信息。16/32/64QAM 信号在小波域所呈现的特征是我们对其进行分类和识别的基础和依据。

对于任意的函数s(t)∈L2(R)的连续小波变换定义为

设接收信号为r(t)=s(t)+ n(t)，0 ≤t≤T，n(t)，为复高斯白噪声，s(t)可表示为s(t)=(t)ej(wct+θc)，式中，ωc为载波频率，θc为载波相位。

对于M－QAM 信号，

式中Ai，Bi∈{2m－1－m，m=1，2，...，M}。

在上式中，S为信号功率，N为符号个数，T为符号周期。

在利用小波变换进行数字信号处理中，需要经过符号率估计、调制方式识别等信号处理过程，其重要依据就是通过对信号的特征参数(幅度突变、相位突变、频率突变)突变的检测与分析。因此小波函数对信号特征参数突变检测能力的高低，是体现小波函数信号处理性能优劣的重要标志。由于Haar 小波函数具有较强的边缘检测性能，并且形式简单，计算方便，因此选取Haar 小波基对QAM 信号进行小波变换，当Haar 小波变换位于一个符号周期内时，QAM 信号的小波变换结果为

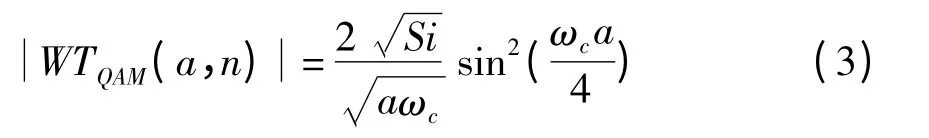
由上式可以看出，在理想情况下，分别由于频率和幅度的变化，MQAM 信号的小波变换模值为多步阶梯函数，在相位发生跳变处会出现明显的峰值。

3 调制样式识别算法

下面给出具体的算法步骤:

(1)对接收到的MQAM 信号进行小波变换，获得信号小波变换模序列，MQAM 信号的小波变换模序列反映了信号幅度，其中16QAM，32QAM，64QAM的小波变换模序列分别有3种、5种和10种不同的稳定电平，当Haar 小波经过符号变化时，信号的小波变换将在符号的交界处产生幅度很大的峰值;

(2)对小波变换模序列进行均值滤波，以滤除峰值及进一步降低噪声，并按从大到小的顺序进行重新排列;

(3)对均值滤波模序列进行差分运算，以提高识别速度;

(4)计算最大值对应位置P，不同进制的QAM信号最大值对应的位置不同，16QAM 在3/4，32QAM 在7/8，64QAM 在15/16，从而设定判决门限为0.8 和0.91，并识别出调制阶数M。

图1 识别算法模型

4 仿真结果

图2－图4 中的第一个图为接收到的MQAM 信号，第二个图为小波变换模序列，第三个图为经过均值滤波的模序列，第四个图为按从大到小顺序重新排列之后的模序列，第五个图为经过差分运算之后的模序列，从该图可以求出最大值对应位置P。通过对P 设置不同的门限就可以对QAM 信号进行有效识别和分类。

5 结束语

本课题提出了一种基于小波变换的QAM 调制样式识别算法并给出了详细推导，该算法的主要思想是利用不同阶数QAM 信号在小波域具有的特征来区分QAM 信号。算法先对接收信号进行小波变换得到模序列，然后分别利用均值滤波消噪和差分运算进行处理，从而通过判断模序列最大值所在位置实现对QAM 阶数的识别。

此算法的优点是能在较低信噪比下进行分类，不需要预先知道信号的波特率、载波频率等参数，并且计算比较简单。最后通过对16/32/64QAM 信号进行计算机仿真，证明了算法的有效性。

［1］王建新，宋辉.基于星座图的数字调制方式识别［J］.通信学报，2004，25(6):166－173.

［2］姜凯，陈卫东.基于星座图聚类分析调制识别的改进算法［J］.信号与信息处理，2009，39(2)，29－31.

［3］李侃，孙进平，印杰.一种PSK/QAM 调制方式识别的似然比方法［J］.电子测量技术，2007，30(2)，6－14.

［4］詹亚锋，曹志刚，马正新.M－QAM 信号的调制制式识别［J］.通信学报，2004，25(2)，68－74.