基于动态属性的数字签名方案
2013-07-19邓宇乔
邓宇乔
广东商学院 数学与计算科学学院,广州 510320
基于动态属性的数字签名方案
邓宇乔
广东商学院 数学与计算科学学院,广州 510320
DENG Yuqiao.Dynamic attribute-based signature scheme.Computer Engineering and Applications,2013,49(15):19-22.
1 引言
基于属性的数字签名是由基于模糊身份签名[1]的概念发展而来,机制更为灵活,其在精确(fine-grained)访问控制的匿名认证系统中发挥了重要的作用。在基于属性的签名体制中,用户从属性中心获得一组属性的私钥,然后用这组属性私钥进行签名。签名者的权力由其所拥有的属性集合决定。验证者通过验证该签名,只能确定该签名满足某个访问结构,但是不知道签名者是如何满足这个访问结构的。2008年Guo等[2]提出了一个在Goyal等[3]的加密方案上构造的属性签名方案,Shahandashti等[4]在Sahai和Waters[5]的加密方案上构造了基于属性的门限签名方案,另外,Chase[6]等提出了多授权中心概念,并给出了一个多授权中心的基于属性的加密方案,用户的多个属性由不同的授权中心监管,并分别对其中的每个属性产生加密私钥。
但是,以上的基于属性的密码体制尚存有一个明显的缺陷,即其属性不具有“动态性”。当系统中的成员属性发生变更后,没有相应的修改机制,需要重新分配属性密钥,这将为系统增添极大负担。文献[7]提出一种具有动态属性的群签名方案,但其方案主要为针对群签名的特性提出的。本文借鉴条件密码方案的思想[8-10],给出一个具有动态属性的一般数字签名方案。在条件密码机制中一段密文如需解密,需要满足某个特定的条件,该条件由条件认证方所认证,如果不满足条件,则解密者无法解密。如满足特定条件,则除了可以解密出明文外,解密者还能得到条件认证方的一个签名。本文利用条件密码的思想,对属性签名方案进行改造,使得传统的属性签名方案能在属性拥有者满足某种特定条件后可以申请动态增加其属性密钥,而其新增的属性密钥的控制权由条件认证方所控制,这种思想的好处在于,其可以大大减轻属性密钥生成方的负担,并且具有认证的功能。随后,本文在选择集合模型[11-15]下证明了该方案的安全性。
2 背景知识介绍
2.1 访问树结构
定义1(访问结构)设{P1,P2,…,Pn}是n个参与者的集合。设Λ表示由参与者集合的子集构成的集合,B,C表示参与者集合的子集,对于所有的B,C:如果B∈Λ并且B⊆C,那么C∈Λ,则说Λ是一个单调的访问结构。一个访问结构(或者单调的访问结构)Λ是一个非空的参与者集合的子集(或者单调子集)构成的集合。设D表示参与者的任一子集,如果D∈Λ,则叫做授权集合,如果D∉Λ则叫做非授权集合。
访问树结构(Access Τree):访问树用于表达一个控制访问结构。每一棵树的非叶子节点都是一个门限,用kx表示该节点的门限值。访问树中的某节点是可访问的,当且仅当该节点的子节点集合中至少有kx个节点是可访问的。而叶子节点则与属性绑定。对于叶子节点x,函数att(x)表示叶子节点相对应的属性。对于任意节点x,函数index(x)表示该节点的索引值,而parent(x)则表示该节点的父节点的索引值。
2.2 基于条件的密码技术
本文在改造属性签名方案中,借鉴了基于条件的密码技术。基于条件的密码技术首先由Kim等在文献[8]中提出,在该文中,他们所构造的基于条件的数字签名主要是针对某个特定的应用场景——数字签名的公平交换而言的。Berta[9]等人把这种技术应用到微型的电子卡片技术中,随后,基于条件的密码技术被Klonowski[10]等人作了有意义的推广,得到了一定的发展。在基于条件的加密方案中,某用户对文档的解密建立在某个条件成立的基础上。本文将使用这种加解密技术以解决属性的动态调整问题。
2.3 双线性映射技术
双线性映射是指具有下面性质的映射:
设G是由P生成的循环加群,其阶为素数q,V是一个阶为q的循环乘群。
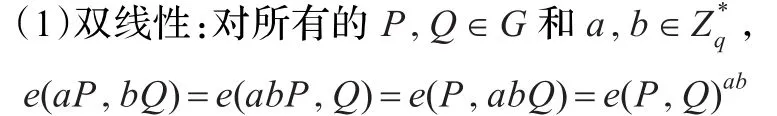
(2)非退化:存在一个P∈G,满足e(P,P)≠1。
(3)可计算:对P,Q∈G,存在一个有效的算法计算e(P,Q)。
2.4 困难性假设
定义2(判定Diffie-Hellman问题(DDH))该假定指的是:设(a',b',c'∈Zp),不存在多项式时间敌手B有不可忽略的优势区分元组(Α'=ga',B'=gb',C'=ga'b')和元组(Α'=ga',B'=gb',C'=gc')。
敌手B解决该问题的优势定义为:
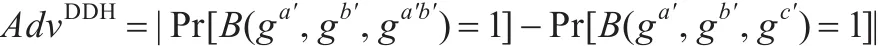
定义3(判定Diffie-Hellman假定(DBDH))该假定指的是:设(a,b,c,z∈Zp),不存在多项式时间敌手B有不可忽略的优势区分元组(Α=ga,B=gb,C=gc,e(g,g)abc)和元组(Α=ga,B=gb,C=gc,e(g,g)z)。敌手B解决该问题的优势为:
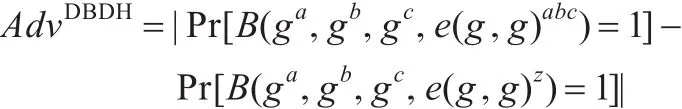
3 基于动态属性的数字签名方案
3.1 方案定义
实现的基于动态属性的数字签名方案主要包含以下六个算法:初始化、密钥产生、生成动态属性密钥、属性密钥提取、签名、验证,具体描述如下:
初始化:该算法接受一个安全参数λ和属性集合U的输入,输出公共参数PK和主密钥MSK。
密钥产生:该算法接受MSK,PK,访问结构Α以及属性集合γ的输入,输出该属性集合的私钥SK。
生成动态属性密钥:该算法接受系统私钥和用户满足某属性所需条件的明文m的输入,输出该属性的动态属性密钥。
属性密钥提取:该算法接受认证方对用户满足某属性的签名SIG的输入,还原该属性的密钥。
签名:该算法接受公钥PK、用户属性私钥以及消息m的输入,输出用户对该消息的签名。
验证:该算法接受公钥PK,消息m以及签名S的输入,如果签名为真,则输出1,否则输出0。
3.2 方案安全模型定义
本文方案的安全模型参考的是选择集合安全模型的定义方法(Selective-Set Model)[3],方案安全模型定义如下:
参数设置:挑战者运行方案的参数设置算法,并把产生的公共参数发送给敌手。
阶段1在该阶段,敌手Α可以询问多个访问结构Λj的动态属性密钥及满足该属性所需具备条件的散列值(即H(m)值),并可将该结构中的任意的动态属性密钥进行提取(即得到其属性密钥),但需满足以下条件:敌手能从动态属性密钥中提取出来的属性密钥集合γ'必须是γ的真子集(即γ'⊂γ),且γ∉Λj。
挑战:在此阶段,敌手提交两个等长的消息M0和M1。挑战者随机抛一枚硬币b,并根据属性集合γ对Mb进行签名,然后把签名发送给敌手Α。
阶段2此阶段与阶段1相同。
猜测:在此阶段,敌手Α输出对b的猜测b'。
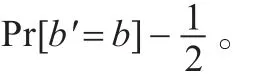
需要注意的是,签名方案的安全性通常是建立在签名的不可伪造性上的,本文所提的签名的安全性为建立在Selective-Set Model模型上,然而,可以看出,如果某个攻击者在计算上甚至无法分清两个等长消息的签名,则他必定是无法伪造出该消息的签名的,因此,本文所提方案在传统签名的不可伪造性上也是成立的。
3.3 方案描述
设G1是一个以素数p为阶的双线性群,g是其生成元。
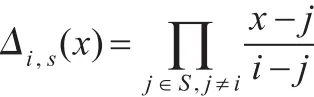
为拉格朗日参数,S是一个在Zp的集合。所有的属性集合为U,而所有属性都与Zp*中的元素关联。
初始化:对于一个集合的属性,为其随机选择Zp上的ti作为属性i的私钥。同时,选择属性认证方的私钥xΑ∈Zp,认证方的公钥为yΑ=gXΑ。并公布属性对应的公钥为而签名者的公钥为Y=e(g,g)y,签名者的主密钥为,属性认证方的私钥为xΑ。
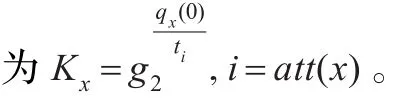
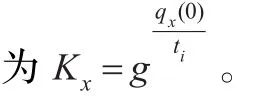
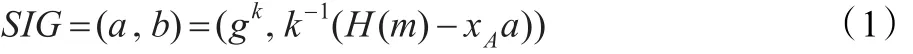
选择随机数k,计算对于消息m的Elgamal签名:如果该签名合法,将满足以下式子:yaab=gH(m)。其中消息m为满足该属性所需的条件。认证方公开a和ab。
该属性的拥有者可计算二元组dk=(a',b')=(Kx*S'z,az),。二元组dk即为动态属性密钥。在此二元组中,维持了本文所提方案的属性密钥的动态性,在下一步密钥提取的过程中,将给出当用户满足某个条件时,如何通过此二元组计算出用户目前尚未满足的某个属性的密钥。
由以上过程可以看到,在计算动态属性密钥时,与具体密文无关,仅需提供属性密钥即可计算。因此,可对具体属性预先计算好其动态属性密钥。
属性密钥提取:当认证方认证某用户满足某属性的条件时,认证方把其签名的参数b发给用户,因而,用户可以得到该属性的密钥:Kx'=a'/b'b=Kx*S'z/azb=Kx。
同时,用户还可以得到认证方颁发的签名SIG=(a,b)。该签名满足:
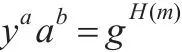
签名:对于属性集合γ和消息M∈G2,签名者选择随机值r,s,用以下方式计算签名:
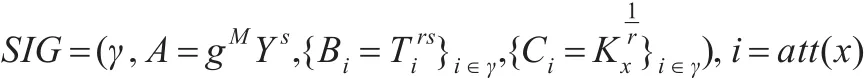
验证:验证过程分成以下步骤:
如果节点x为叶子节点,则计算:
Dx=e(Ci,Bi)=(x为i对应的属性的节点序号)
如果节点x为非叶子节点,则签名者的身份属性中必定包含至少有kx个子节点的值是满足访问结构要求的。定义Sx表示这kx个子节点值的集合,定义Fz表示节点z所表示的值,通过拉格朗日插值定理,可以得到:
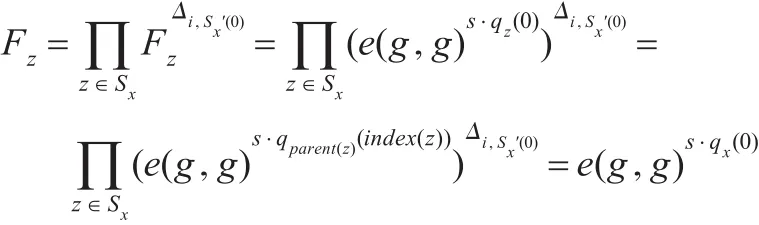
其中,i=index(z),Sx'={index(z):z∈Sx}。
假设某用户的属性满足其签名的权限,则验证者能根据用户最终解出访问树根节点的值:Fr==e(g,g)sy。
随后,验证者验证是否有:gM=E'/e(g,g)sy成立。
4 方案安全性证明
定理1假定以上的定义2、定义3的问题难解,则本文所述方案是安全的,即在Seletive-Set游戏中,敌手的优势是可忽略的。
证明假设存在一个多项式时间的敌手Α能在Seletive-Set游戏中破解本文的方案,将构造一个模拟器B同时解决本文定义2至定义3中的两个问题。
首先,挑战者设置一个双线性映射e和群G1,G2,并给定生成元g。挑战者投掷硬币μ,如果μ=1,则设置(Α,B,C,D,Α',B',C')=(ga,gb,gc,e(g,g)abc,ga',gb',ga'b');如果μ=0,则设置(Α,B,C,D,Α',B',C')=(ga,gb,gc,e(g,g)z,ga',gb',gc')。
初始化:模拟器运行算法Α,Α选择它需要挑战的属性集合γ。
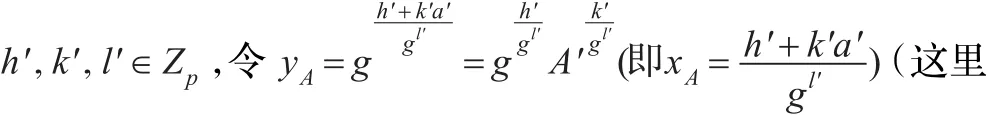
的h'将表示某个动态属性的满足条件明文的散列值,即h'=H(m))。随后,模拟器公开上述公共参数。
阶段1在该阶段中,为了简化描述,分为两种情况讨论。
(1)敌手提取了γ中所有的属性密钥
这种情况下,即敌手知道了γ中所有的属性密钥,此时动态属性密钥的作用消失了(也即敌手满足了所有动态属性密钥的条件)。
此时按以下两种方法构造访问树中某棵子树的根节点的多项式:
PolySat(Tx,γ,λx):这种情况下,Tx(γ)=1,即根节点为x的树能被访问结构γ访问。此时,选取根节点x的多项式qx,使得qx(0)=λx(λx∈Zp为已知),随后,选取该根节点每一个孩子x'的多项式qx',使得qx'(0)=qx(index(x'))。
PolyUnsat(Tx,γ,gλx):这种情况下,Tx(γ)=0,即根节点为x的树不能被访问结构γ访问。此时只知道gλx的值。定义一个度为dx的多项式qx,令qx(0)=λx,由于Tx(γ)=0,所以,访问结构中满足条件的节点不多于dx个,设hx≤dx为满足条件的节点个数,对于满足条件的节点x',设qx(index(x'))=λx',λx'∈Zp,由于qx是度为dx的多项式,所以可以选取不多于dx个节点的值。算法递归地调用以下两个方法设置该树以下的节点的多项式:
PolySat(Tx',γ,λx'):如果x'满足条件,此时λx'已知,故可以直接构造。
PolyUnsat(Tx',γ,):如果x'不满足条件,此时只知道的值(因为在此情况下,事实上只知道的值)。
最后,模拟器执行PolyUnsat(T,γ,Α)来定义整棵访问树的根节点的多项式。可以发现,对于每一个节点x,如果该节点满足条件,则必然知道λx的值,否则,至少知道gλx的值。随后,模拟器定义多项式Qx(.)=bqx(.),所以,对于根节点r的多项式Qr而言,有Qr(0)=ab。以下定义叶子节点对应的Kx值如下:
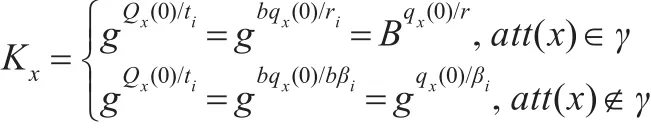
(2)敌手仅提取了部分的动态属性密钥
即敌手至少有一个属性att(x)的属性密钥未知,而仅知道其对应的动态属性密钥。当敌手询问的动态属性att(x')≠att(x)时,随机选取t',m'∈,令H(m)=m',计算SIG=(a,b)=(gt',t'-1(m'-xΑa)),则该属性对应的动态密钥为dk=(a',b')=(Kx'*abz,az),z∈。
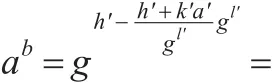
挑战:敌手Α提交两个等长的消息M0,M1,挑战者随机抛一枚硬币b,随机选取r∈,并公布以下签名:
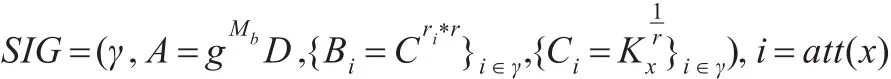
如果μ=1,则密文和动态密钥都为合法的构造,如果μ=0,则(D,C')=(e(g,g)z,gc')均为随机数。
阶段2该阶段与阶段1过程一样。
猜测:Α提交对b的猜测b',如果b'=b,则模拟器输出μ=1表示这是合法的DH和DBDH问题的元组,否则,模拟器输出μ=0。
假设敌手Α攻破本系统的优势为ε,那么根据概率的知识容易知道,模拟器攻破以上两个难题的优势为ε/2。
5 结论
基于属性的数字签名方案能很好地解决签名者的身份隐私问题,但由于其属性不具有“动态”的特性,导致了用户在属性迁移时的不便。本文利用“条件”的思想,把方案中的属性改成动态的形式,当用户的属性变迁后,他可以通过与认证机构的交互,自己计算出新增的属性密钥,从而较好地实现了用户权限的灵活控制。
[1]Yang P,Cao Z,Dong X.Fuzzy identity based signature,Report 2008/002[EB/OL].[2012-11-21].http://eprint.iacr.org/2008/002.
[2]Guo S,Zeng Y.Attribute-based signature scheme[C]//International Conference Information Security and Assurance(ISA 2008),2008:509-511.
[3]Goyal V,Pandey O,Sahai A,et al.Attribute-based encryption for fine-grained access control of encrypted data[C]//Proc of CCS.New York:ACM Press,2006:89-98.
[4]Shahandashti S F,Safavi-Naini R.Τhreshold attribute-based signatures and their application to anonymous credential systems[C]//LNCS 5580:AFRICACRYPΤ 2009.Berlin:Springer-Verlag,2009:198-216.
[5]Sahai A,Waters B.Fuzzy identity-based encryption[C]//LNCS 3494:AdvancesinCryptology-EUROCRYPΤ 2005.Aarhus:Springer-Verlag Press,2005:457-473.
[6]Chase M.Multi-authority attribute based encryption[C]//Vadhan S P.Lecture Notes in Computer Science ΤCC,2007:515-534.
[7]Emura K,Miyaji A,Omote K.A dynamic attribute-based group signature scheme and its application in an anonymous survey for the collection of attribute statistics[C]//International Conf on Availability,Reliability and Security,2009.
[8]Lee B,Kim K.Fair exchange of digital signatures using conditional signature[C]//Symposium on Cryptography and Information Security,Shirahama,Japan,2002:179-184.
[9]Berta I Z,Buttyn L,Vajda I.Migrating the untrusted terminal problem using conditional signatures[C]//International Conference on Information Τechnology:Coding and Computing(IΤCC),2004.
[10]Marek K,Mirosław K,Anna L.Conditional digital signatures[C]//LNCS 3592:ΤrustBus 2005,2005:206-215.
[11]陈少真,王文强,彭书娟.高效的基于属性的环签名方案[J].计算机研究与发展,2010,47(12):2075-2082.
[12]孙昌霞,马文平,陈和风.多授权中心的基于属性的签名[J].四川大学学报:工程科学版,2011,43(1):83-86.
[13]Lewko A,Waters B.Unbounded HIBE and attribute-based encryption[C]//Proceedings of the 30th Annual International Conference on Τheory and Applications of Cryptographic Τechniques:Advances in Cryptology,EUROCRYPΤ’11,2011.
[14]Lewko A,Okamoto Τ.Fully secure functional encryption:attribute-based encryption and(hierarchical)inner product encryption[EB/OL].[2012-11-21].http://eprint.iacr.org/2010/110.
[15]Ostrovsky R,Sahai A,Waters B.Attribute based encryption with non-monotonic access structures[C]//ACM Conference on Computer and Communications Security(ACM CCS),2007.
DENG Yuqiao
Mathematics and Computer Science College,Guangdong University of Business Studies,Guangzhou 510320,China
Τhe user’s privacy can be well protected using attribute-based signature scheme.But the attributes are static in all attribute-based signature schemes,which are due to certain problems in practical applications:when the member’s attribute has been changed,there is no corresponding mechanism to re-assign the attributes key,which will cause tremendous burden.Based on conditions-based encryption,this paper develops a dynamic attribute-based signature scheme.User is allowed to calculate its own attributes key in the scheme once it satisfies certain attribute after the authenticating party’s digital signature is given.Τhe security of the scheme is discussed.
attribute signature scheme;conditions encryption scheme;dynamic;bilinear pairings
基于属性的数字签名方案能很好地实现用户身份的隐藏。但所提出的签名方案中,用户属性都是静态的,当系统中的成员属性发生变更后,没有相应的修改机制,需要重新分配属性密钥,这将为系统增添极大负担。在实际应用中存在问题。基于条件加密的思想,设计了一个具有动态属性的数字签名方案,该方案能在该用户满足某属性后,由认证方给用户提供签名,并让用户自行计算其属性密钥。对签名方案的安全性进行了讨论。
属性签名;条件加密;动态;双线性对
A
ΤP309
10.3778/j.issn.1002-8331.1301-0232
广东省自然科学基金(No.S2012010010376);广东省育苗项目(No.LYM11068)。
邓宇乔(1980—),男,博士,主要从事密码学,安全电子支付,数字版权管理系统方面的研究。E-mail:dengyuqiao80@yahoo.cn
2013-01-21
2013-05-09
1002-8331(2013)15-0019-04
CNKI出版日期:2013-05-15 http://www.cnki.net/kcms/detail/11.2127.ΤP.20130515.1015.006.html
