人工鱼群算法在桥梁传感器优化配置中的应用

赵宇，彭珍瑞，殷红

兰州交通大学机电工程学院，兰州 730070

人工鱼群算法在桥梁传感器优化配置中的应用

赵宇，彭珍瑞，殷红

兰州交通大学机电工程学院，兰州 730070

1 引言

目前，国内外桥梁结构健康监测系统的研究与应用已取得了一定的成果与进展，传感器子系统作为其中不可或缺的重要部分，在桥梁结构健康监测系统中为反映桥梁结构健康状况信息的获取奠定了基础[1]。如何在最小的经济投入下，使用最少的传感器获取最全面的信息，是一个完整桥梁健康监测系统所需解决的问题之一。黄民水[2]等人在基本遗传算法的基础上进行改进，提出了一种基于二重结构编码的遗传算法桥梁结构传感器优化配置方法；田莉[3]等人基于自适应模拟退火遗传算法研究了传感器的优化配置。采用随机类算法（如遗传算法、模拟退火算法、粒子群算法等）来进行传感器的优化配置，是目前研究桥梁结构健康监测传感器优化配置的热点，但这些算法收敛速度慢精度低，易早熟陷入局部最优。

人工鱼群算法（Artificial Fish School Algorithm，AFSA）是一种基于动物行为的仿生类新型智能优化算法，模拟鱼群在觅食过程中的行为，通过鱼群中人工鱼之间的协作达到群体最优。人工鱼群算法已经在参数估计[4]、聚类分析[5]、神经网络[6]、故障诊断[7]等方面的到了应用，并取得了较好的效果。本文采用人工鱼群算法对桥梁结构健康监测传感器进行优化配置，经比较，其结果优于粒子群算法（Particle Swarm Optimization，PSO）。

2 人工鱼群算法的描述

人工鱼群算法是李晓磊[8]等提出的一种基于鱼类觅食、聚群、追尾、随机等行为的群体智能优化算法。

在求解问题时，首先初始化鱼群，鱼群中每条人工鱼是给定范围内的随机n维数组。设一条人工鱼的当前位置为Xi=(x1，x2，…，xn)，感知范围为Visual，某时刻所在位置在求解极小值问题中，若该时刻所在位置目标函数值Yν=f(Xν)即食物浓度低于当前位置食物浓度Yi，则人工鱼向该位置前进，到达位置Xnext：

其中，r为[0，1]之间的随机数；Step为步长。若该位置食物浓度Yν高于当前位置，则继续对周围环境做出巡视。人工鱼群算法就是基于观测感知范围内其他人工鱼食物浓度决定自身前进方向这种思想实现寻优过程的。

图1 桥梁平面布局图（单位：mm）

3 基于人工鱼群算法的桥梁传感器优化配置

3.1 桥梁传感器优化配置数学模型

首先，建立桥梁有限元模型，进行模态分析，提取其模态振型。设桥梁有限元模态振型矩阵Φn×l，n为有限元模型节点自由度即传感器待配置点的自由度，l为模态振型的阶数。从中选取m个自由度作为传感器最终配置点，使目标函数MAC矩阵的非对角线元达到最优，即：

桥梁传感器优化配置作为一种典型的组合优化问题，要求使用最少的成本将传感器配置在最合理的位置，使得传感器所测得的信息能够真实的反映桥梁的健康状况，为桥梁状态的评估提供依据。而人工鱼群算法在对问题目标函数最优解的搜索过程中，有一定的自适应力，可以并行搜索，具有较强的全局优化能力。故运用人工鱼群算法求解桥梁传感器优化配置的数学模型所得的目标函数，解决了这一优化问题。

3.2 桥梁传感器优化配置算例

本文对一座主桥（21 133.4+33 509.8+21 133.4）的拱桥[10]进行传感器优化配置，桥面宽度8 000 mm，主要结构由梁和板材料（桥面材料厚度为12 mm）组成。桥面材料的弹性模量为E=1.6×105MPa，泊松比为0.35；其他梁材料的弹性模量为E=2.06×105MPa，泊松比为0.3。桥梁平面布局图如图1所示。

利用ANSYS13.0建立拱桥有限元模型，其中桁架采用BEAM188单元模拟，桥面板采用SHELL63单元模拟，有限元模型如图2所示。对桥梁结构进行模态分析，提取前l阶振型，构造模态振型矩阵Φn×l，n为节点自由度即传感器待配置点的自由度，为了便于计算将节点自由度从小到大进行编号，假定单个节点自由度为3，则编号为1，2，…，3n。将该矩阵作为人工鱼群算法解决桥梁传感器优化配置问题的基本数据，用于求得MAC矩阵。

图2 桥梁有限元模型图

3.3 人工鱼群算法在桥梁传感器优化配置中的应用

3.3.1 人工鱼群算法的三种行为

人工鱼群算法主要有觅食、聚群、追尾等行为。模拟鱼群趋向食物的行为，称为觅食行为。设人工鱼当前位置Xi，感知范围内的某一位置Xj，若当前食物浓度Yi＞Yj，则向Xj方向前进一步；否则，继续尝试try_number次。若仍不满足前进条件，则随机移动一步，随机行为就是在感知范围内随机的选择移动方向。

鱼类大量或少量的进行聚群行为，觅食或躲避敌害。设人工鱼当前位置Xi，感知范围内其他人工鱼的数目nf，当前中心位置Xc，食物浓度Yc。若＜δYi（δ为拥挤度因子），表明当前中心位置有较多食物并且周围不太拥挤，人工鱼向当前中心位置Xc方向前进一步；否则，执行觅食行为。同时，某一条人工鱼Xj，食物浓度Yj。若＜δYi，表明当前位置有较多食物并且周围不太拥挤，人工鱼向当前位置Xj方向前进一步，附近的人工鱼会尾随其后游过来，完成追尾行为；否则，执行觅食行为。

人工鱼通过以上几种行为感知周围环境，在所对应问题中，某条人工鱼表现出的状态即为目标函数最优解。

3.3.2 人工鱼群算法桥梁传感器优化配置步骤

在人工鱼群算法求解桥梁传感器优化配置问题中，每条人工鱼作为传感器候选配置点，MAC矩阵最大非对角元最小时的人工鱼所对应的点为传感器的最终配置点。

（1）初始化鱼群，针对桥梁传感器优化配置问题，初始化鱼群，人工鱼群大小为N，随机产生n行N列初始鱼群，n为节点自由度即传感器待配置点的自由度，人工鱼行号与节点自由度编号相对应，每列表示一条人工鱼的传感器待配置点，每条人工鱼取[0，1]范围的随机数。设置最大迭代次数MAXGEN，觅食行为尝试次数try_number，感知范围Visual，步长Step以及拥挤度因子δ。

（2）计算各条人工鱼的目标函数值，根据有限元模态分析后构造的模态振型矩阵Φn×l，n为节点自由度即传感器待配置点的自由度，按式（2）给出的目标函数，随机选取其中m(2＜m＜n)行求得的MAC矩阵最大非对角元，m为传感器最终配置点自由度。

（3）对人工鱼群执行聚群行为、追尾行为，选择目标函数值小的方向为移动方向，若两种行为均不满足前进条件，则执行觅食行为，若达到觅食行为最大尝试次数try_number时仍不满足前进条件，则执行随机行为。

（4）重新计算各条人工鱼的目标函数值，判断是否达到最大迭代次数，是则继续下一步，否则执行步骤（3）。

（5）确定最优解，即MAC矩阵最大非对角元最小时的配置点为最优解，此时传感器最终配置点自由度m及MAC矩阵最大非对角元均为最优。

人工鱼群算法流程图如图3所示。

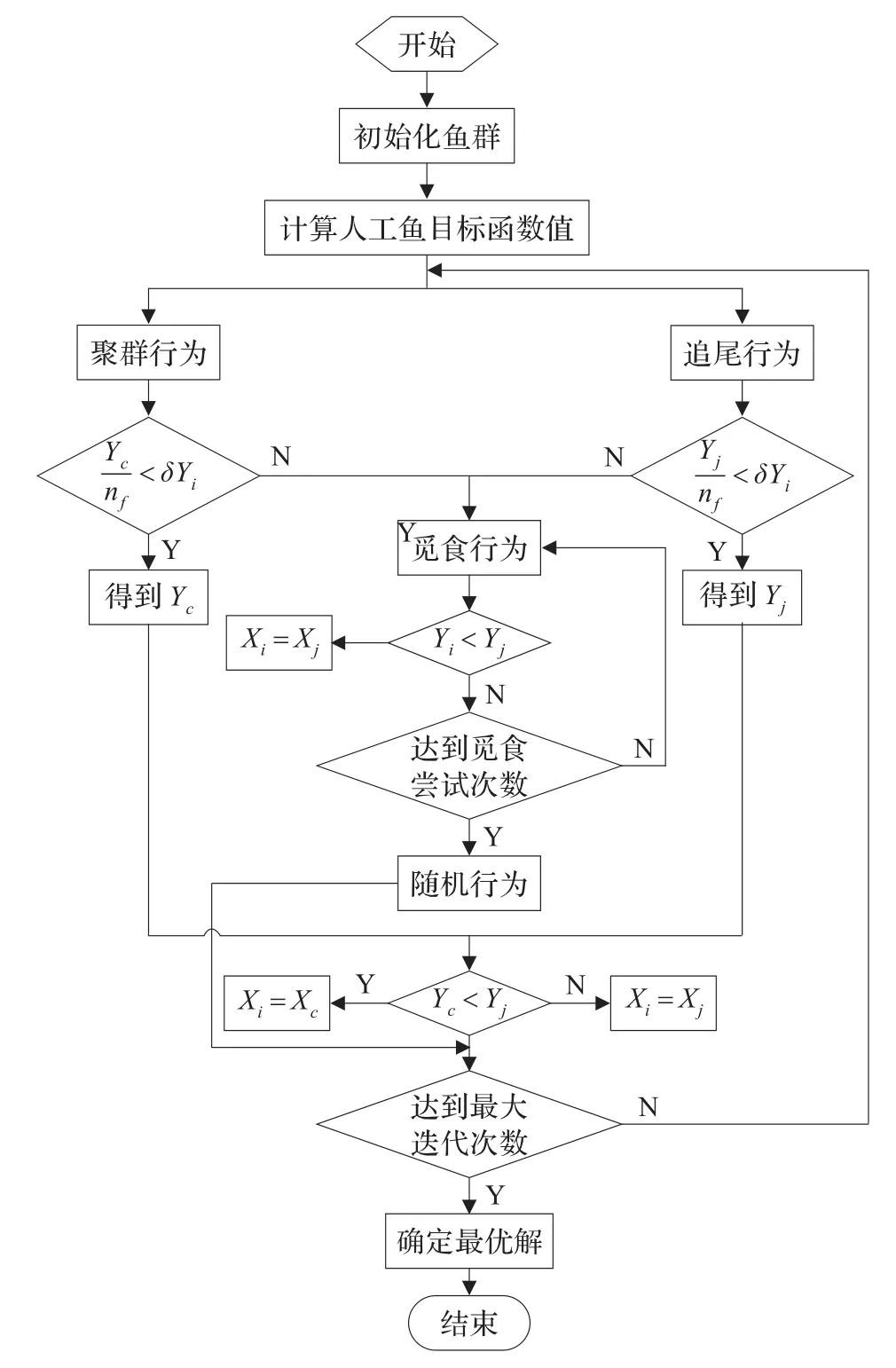
图3 人工鱼群算法流程图

4 仿真实验

在图2桥梁有限元模型中，全桥共划分12 631个单元，11 332个节点，提取模型前6阶振型。选取桥面主梁与主拱拉梁及副拱立柱连接处作为传感器候选测点，由于桥梁结构对称，选择桥梁1/4结构进行传感器优化配置，其他部分参照配置。共26个节点，每个节点3个自由度，即x、y、z方向的平动，共78个自由度，模态振型矩阵Φ78×6。候选测点示意图如图4所示，并将节点自由度从小到大进行编号1，2，…，78。例如，节点12的3个自由度编号为1、2、3。

图4 传感器候选测点示意图

4.1 人工鱼群算法参数选取

根据人工鱼群算法的流程，利用MATLAB R2009b编程对算例进行求解。针对参数的不同设置对桥梁结构健康监测传感器优化配置结果的影响，通过多次实验测试，对各参数进行调整，观察各参数的取值对优化值（目标函数值MAC矩阵的最大非对角线元最小）的影响。初选人工鱼群大小N=100，最大迭代次数MAXGEN=150，觅食行为尝试次数try_number=5，感知范围Visual=0.5，步长Step=0.1，拥挤度因子δ=0.5。

4.1.1 觅食行为尝试次数try_number与优化值

人工鱼群大小N、最大迭代次数MAXGEN、感知范围Visual、步长Step、拥挤度因子δ均为初选值，对觅食行为尝试次数try_number取不同的值，程序运行20次，它与优化值关系如图5所示。

图5 try_number与优化值关系曲线图

从图5来看，当try_number在10到45之间时，优化值在0.04到0.05之间且波动不大；当try_number=95时，优化值达到最大0.102 5，误差较大。

4.1.2 拥挤度因子δ及感知范围Visual与优化值

其他参数均为初选值，运行程序，观察不同拥挤度因子δ及感知范围Visual对优化值的影响，关系曲线如图6所示。

由图6可知，δ在0.5到2.0之间所对优化值较小，Visual在1之后，优化值在0.032到0.042之间。总体来看，当δ的取值在0.5到2.0之间，Visual为3时优化值较小，其他取值对优化值影响较大。

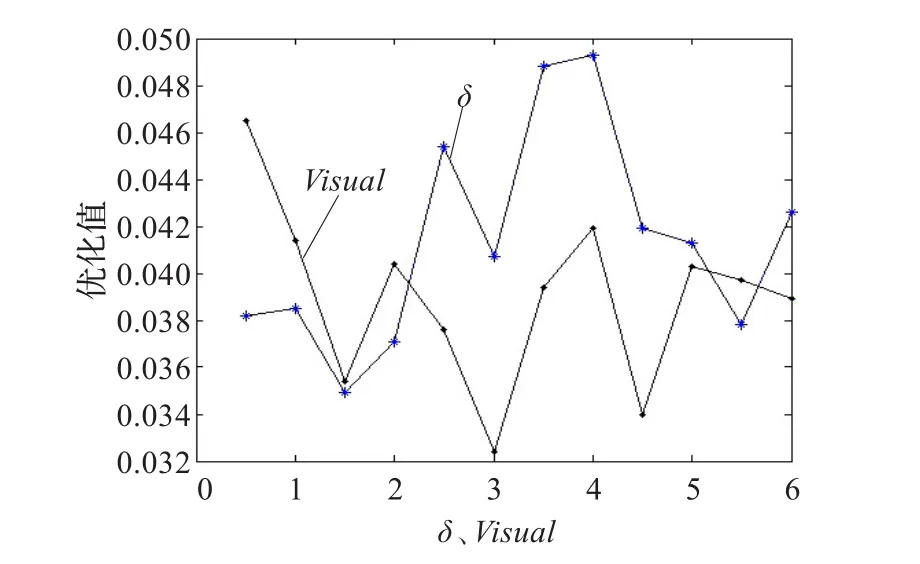
图6 δ、Visual与优化值关系曲线图

4.1.3 步长Step与优化值

参数选取同上，调整步长Step，测试结果如图7所示。

图7 Step与优化值关系曲线图

从测试结果可以看出，在0.1到0.4之间，随着Step的增加，优化值会变大，但是当达到0.4以后，优化值又逐渐减小，随后有波动，Step为1时最小，Step在1.4到2.0之间优化值变化不大。

综合考虑各参数设置与优化值的关系，最终选取所用传感器最少且MAC矩阵的最大非对角线元最小时所对应的参数值，参数设置如表1所示。

表1 人工鱼群算法参数设置

4.2 桥梁传感器优化配置

根据以上参数设置运行程序，从78个自由度选择m(2＜m＜78)个自由度配置传感器，各自由度所对应MAC矩阵的最大非对角线元，如图8所示。自由度在2到10之间MAC矩阵的最大非对角线元迅速减小，10到20之间其值平稳，自由度在20以后缓慢增大。当自由度为10时，可达到传感器配置要求（MAC矩阵的非对角线元越接近于0越好），MAC矩阵的最大非对角线元为0.029 5，故所选传感器数目为10个。传感器配置方案如表2所示。

图8 MAC矩阵的最大非对角线元变化曲线图

表2 传感器配置方案

4.3 结果对比

为了评价基于人工鱼群算法的桥梁传感器优化配置方法的优劣，将人工鱼群算法与基于粒子群算法的传感器优化配置方法进行比较，收敛对比曲线如图9所示。

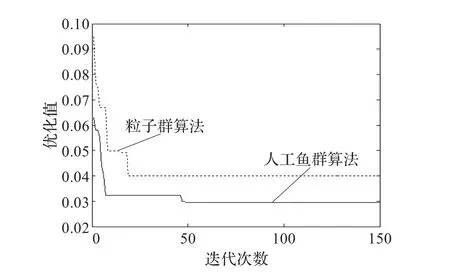
图9 人工鱼群算法与粒子群算法收敛曲线对比图

由图9可以看出，在第1到7次迭代过程中，人工鱼群算法快速收敛到0.033 0，随后继续收敛且在第48次迭代后达到传感器配置要求（MAC矩阵的最大非对角线元为0.029 5），而粒子群算法得到的MAC矩阵的最大非对角线元为0.040 0。人工鱼群算法迭代速度稍慢于粒子群算法，但人工鱼群算法自适应能力强，收敛精度高，克服了一般算法过早收敛陷入局部最优的问题，可以实现桥梁结构健康监测传感器优化配置。

5 结论

本文提出了针对桥梁结构健康监测传感器优化配置问题的人工鱼群算法。为了更好地实现算法在该问题中的应用，通过多次实验测试观察各参数对算法性能的影响，最终选取传感器配置最优的参数设置，提高了人工鱼群算法求解桥梁传感器优化配置问题的精度，实现了人工鱼群算法在组合优化问题上的又一应用。

[1]李爱群，缪长青.桥梁结构健康监测[M].北京：人民交通出版社，2009：157-173.

[2]黄民水，朱宏平，李炜明.基于改进遗传算法的桥梁结构传感器优化布置[J].振动与冲击，2008，27（3）：82-87.

[3]田莉，陈换过，祝俊，等.基于自适应模拟退火遗传算法的传感器优化配置研究[J].振动工程学报，2012，25（3）：238-243.

[4]李晓磊，薛云灿，路飞，等.基于人工鱼群算法的参数估计方法[J].山东大学学报：工学版，2004，34（3）：84-87.

[5]苏锦旗，吴慧欣，薛惠锋.基于人工鱼群算法的聚类挖掘[J].计算机仿真，2009，26（2）：147-150.

[6]张颖.基于改进鱼群算法的BP神经网络优化设计[D].广州：华南理工大学，2012.

[7]陈安华，周博，张会福，等.基于改进人工鱼群算法的机械故障聚类诊断方法[J].振动与冲击，2012，31（17）：145-148.

[8]李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法[J].系统工程理论与实践，2002，22（11）：32-38.

[9]刘寒冰，吴春利，程永春.不同适应度函数的遗传算法在桥梁结构传感器布设中的应用[J].吉林大学学报：工学版，2012，42（1）：51-56.

[10]涂振飞.ANSYS有限元分析工程应用实例教程[M].北京：中国建筑工业出版社，2010：83-94.

[11]吴月萍，杜奕.改进的人工鱼群算法的参数分析[J].计算机工程与应用，2012，48（13）：48-52.

[12]Kammer D C.Sensor placement for on orbit modal identification of large space structures[J].Journal of Guidance，Control，and Dynamics，1991，14（2）：252-259.

[13]Li D S，Li H N，Fritzen C P.The connection between effective independence and modal kinetic energy methods for sensor placement[J].Journal of Sound and Vibration，2007，305（4/5）：945-955.

[14]路杨，张晓丽.CW-PSO及其在古建筑传感器优化配置中的应用研究[J].计算机工程与应用，2013，49（5）：268-270.

[15]林贤坤，覃柏英.微粒算法在传感器优化配置中的应用[J].控制工程，2013，20（1）：84-92.

ZHAO Yu,PENG Zhenrui,YIN Hong

School of Mechatronics Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

In order to achieve optimal sensor placement for bridge structural health monitoring,using less sensors gain as many as information reflect health status of bridges structural,artificial fish school algorithm is applied in an arch bridge,to solve optimal sensor placement problem for bridge with three typical behaviors of artificial fish.The results show that artificial fish school algorithm has high self-adaptive ability and precision,can achieve optimal sensor placement for bridge structural health monitoring.

artificial fish school algorithm;optimal sensor placement;bridge structural health monitoring

为了实现桥梁结构健康监测传感器的优化配置，用尽可能少的传感器获取尽可能多的反映桥梁结构健康状况的信息，将人工鱼群算法应用于一座拱桥的传感器配置中，利用人工鱼的三种典型行为，解决桥梁传感器优化配置问题。结果表明，人工鱼群算法自适应能力强，收敛精度高，可以实现桥梁结构健康监测传感器优化配置。

人工鱼群算法；传感器优化配置；桥梁结构健康监测

A

TP18

10.3778/j.issn.1002-8331.1305-0063

ZHAO Yu,PENG Zhenrui,YIN Hong.Optimal sensor placement for bridge structural health monitoring based on artificial fish school algorithm.Computer Engineering and Applications,2013,49（19）：260-264.

赵宇（1990—），女，硕士研究生，主要研究方向为智能算法桥梁结构健康监测；彭珍瑞（1972—），男，博士，教授；殷红（1978—），女，博士研究生，副教授。E-mail：zhaoyulzjtu@163.com

2013-05-09

2013-07-22

1002-8331（2013）19-0260-05