基于双层微粒群优化的机器人全局路径规划
2013-07-19曾现峰张勇
曾现峰,张勇
1.中国矿业大学信息与电气工程学院,江苏徐州 221116
2.江苏联合职业技术学院徐州机电工程分院,江苏徐州 221011
基于双层微粒群优化的机器人全局路径规划
曾现峰1,2,张勇1
1.中国矿业大学信息与电气工程学院,江苏徐州 221116
2.江苏联合职业技术学院徐州机电工程分院,江苏徐州 221011
1 引言
路径规划是机器人能够完成给定任务的前提,解决的问题是:在已知或未知的环境中,寻找一条从起点到终点的满足一定优化指标的无碰撞路径。根据机器人对环境的掌握状况,已有的路径规划方法可分为基于模型的全局路径规划和基于信息检测的局部路径规划,其中,全局路径规划的基本问题是环境建模和路径寻优。当环境模型已知时,全局路径规划的重点在于开发高性能的搜索算法,使得规划的路径全局最优。目前,用于全局路径规划的方法主要有基于图论、栅格等的传统方法[1]和基于进化算法的智能方法[2-3]。这些方法各具优点,但又都有不足之处[4-6]。针对环境的特点和优化的性能指标,研究不同的路径规划方法,具有重要的意义,是提高路径规划性能的有效途径。
微粒群优化是Kennedy等借鉴鸟群的集体捕食行为,提出的一种随机群进化方法[7]。相对传统的优化方法,该方法易于实现,可调参数少,收敛速度快,已成功应用于函数优化、模式识别、神经网络训练、数据挖掘,以及路径规划等领域。但是,利用微粒群优化进行机器人路径规划,存在局部收敛,效率低下,以及精度不高等缺点,尤其是含有非规则密集障碍物的复杂环境,优化的路径多与障碍物碰撞。文献[8]提出一种改进的微粒群优化方法,先用神经网络训练碰撞罚函数,得到无碰撞的路径,再用微粒群优化求解路径最优问题;文献[9]提出一种蚁群微粒群优化方法,先用微粒群优化得到蚁群优化的初始信息素分布,再用蚁群优化搜索全局最优路径。该方法有效结合了微粒群优化和蚁群优化的优点,具有速度快和精度高等优点。
针对微粒群优化用于密集障碍物环境机器人全局路径规划存在的问题,本文提出一种双层微粒群优化方法(Two-Layer Particle Swarm Optimization,TL-PSO)。该方法通过底层微粒群优化,得到若干最优路径;通过顶层微粒群优化,在这些最优路径附近局部搜索,从而得到机器人的全局最优路径;通过对不可行路径实施脱障操作,使其成为可行路径。多场景的机器人路径规划结果表明,本文方法能够找到机器人的全局最优路径。
2 问题建模
为了规划机器人路径,首先需要建立问题的数学模型。如图1所示,在机器人工作空间建立两维绝对坐标系O-XY,其中,S为机器人的起点,G为终点,多边形物体表示障碍物。当起点与终点的连线与X轴不重合时,建立如下相对坐标系S-xy:以S和G间的连线为x轴,过S点且垂直SG的直线为y轴[10]。两坐标系间的变换公式为:
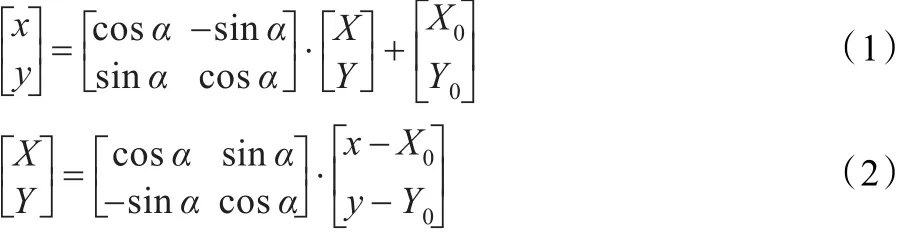
式中,(X,Y)和(x,y)分别为点在坐标系O-XY和S-xy的坐标,α为坐标轴X与x的夹角,(X0,Y0)为S在坐标系O-XY的坐标。
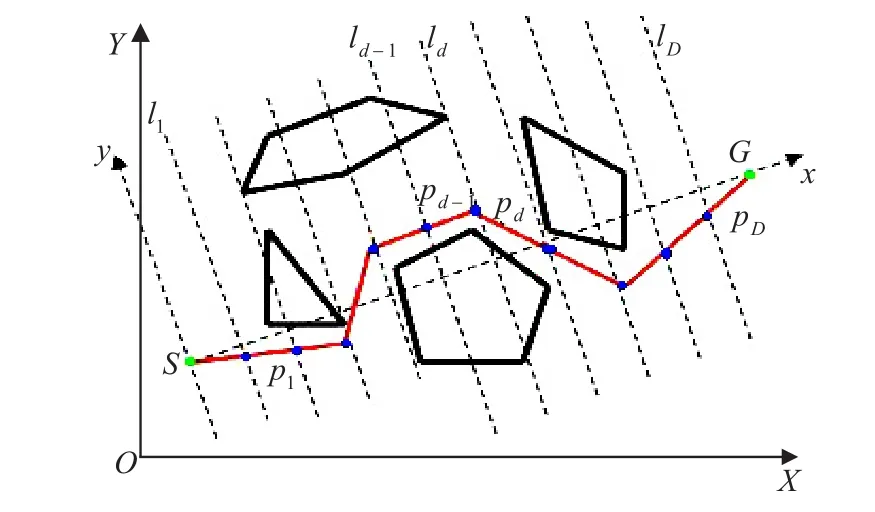
图1 环境模型
对线段SG进行D+1等分,并过每个等分点作SG的垂线,可以得到平行直线族(l1,…,ld-1,ld,…,lD),该直线族与路径的交点,即为规划的目标点序列(p1,…,pd-1,pd,…,pD)。
机器人路径规划,就是在相对坐标系S-xy中,寻找一个目标点序列(p1,…,pd-1,pd,…,pD),使得构成的路径


式中,LSG为S和G间的距离。
机器人路径规划问题,可以建模为一个约束优化问题,通过惩罚不可行路径,得到如下无约束优化问题:
minF(p)=L(p)·(1+N(p))(5)式中,N(p)为p与障碍物碰撞的次数。由式(5)可知,p与障碍物碰撞的次数越多,受到的惩罚程度越大,该路径的性能越差。
3 本文方法
本文提出的基于双层微粒群优化的机器人全局路径规划的思想是:通过底层微粒群优化,得到若干最优路径;通过顶层微粒群优化,在这些最优路径附近局部搜索,得到机器人的全局最优路径;通过对不可行路径实施脱障操作,使其成为可行路径。
3.1 双层微粒群优化
对于含有密集障碍物的环境,采用微粒群优化进行机器人全局路径规划,得到的结果多为非可行路径。即使路径是可行的,也多为局部最优的。通过调整微粒群优化的参数,虽然可以在一定程度上提高规划后路径的性能,但是,性能的提高往往很有限。为了提高机器人路径的全局性能,这里提出一种新的微粒群优化方法,即双层微粒群优化。
该方法的思想是:微粒群优化包含2层,即底层和顶层优化。其中,底层微粒群优化在决策空间广度搜索,得到若干最优路径;顶层微粒群优化基于这些最优路径,进行深度搜索,得到机器人的全局最优路径。
传统的微粒更新公式如下[7]:
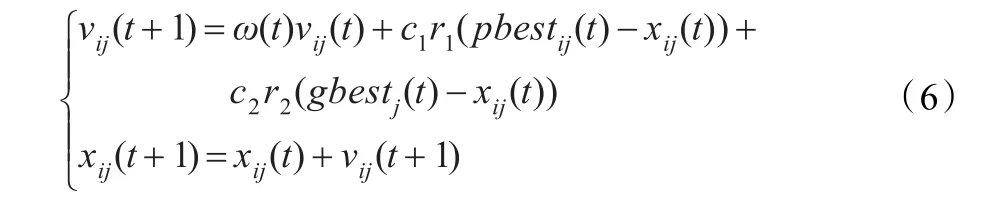
式中,i=1,2,…,N,N为微粒群规模;j=1,2,…,D,D为决策空间的维数;pbest和gbest分别为微粒的个体极值点和全局极值点;c1和c2是两个学习因子,通常取c1=c2=2;r1和r2是(0,1)之间的随机数;ω是惯性权重,用来控制前次迭代的速度对当前迭代速度的影响,以协调微粒的广度和深度搜索。为了增强底层微粒群优化的广度搜索性能,更新微粒的速度时,采用下式线性递减惯性权重:

式中,ωmax和ωmin分别为惯性权重的最大和最小值,本文取ωmax=0.9,ωmin=0.4;t和T分别为当前和最大迭代次数。
顶层微粒群优化基于底层微粒群优化得到的最优路径,进行深度搜索。更新微粒的速度时,惯性权重ω和学习因子c1线性递减,学习因子c2线性递增,其取值如下:

式中,cmax和cmin分别为学习因子的最大和最小值,本文取cmax=2.5,cmin=0.5。
3.2 脱障操作
采用微粒群优化进行机器人路径规划时,如果能够根据机器人的起点和终点位置,以及障碍物的位置,引导微粒的搜索,那么,将会提高优化解成为可行路径的概率。基于此,当某路径不可行时,说明该路径的某段与障碍物相交,对该路径实施脱障操作,也即对微粒的相应分量定向定步长变异,以避免机器人与障碍物碰撞。

由式(9)可知,当ymin≥0 或ymax>|ymin|时,整个障碍物或其大部分位于x轴的上方;相反,当ymax<0 或ymax≤|ymin|时,整个障碍物或其大部分位于x轴的下方。通过变异使路径点pd和pd+1向x轴平移l,可以远离障碍物Obj,进而使路径成为可行的。由式(5)可知,这样可以提高微粒的适应值。
图2给出了脱障操作的过程。图中,I线为原来的路径,由于与障碍物相交,因此,是不可行的;II线为脱障操作后得到的路径,不再与障碍物相交,从而成为可行路径。
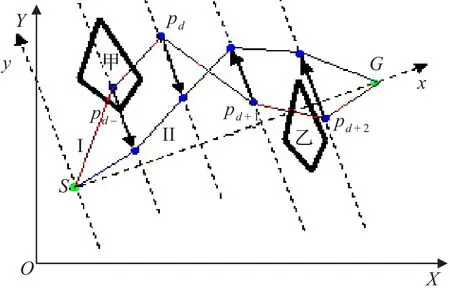
图2 脱障操作过程
需要注意的是,对微粒实施脱障操作后,如果微粒的某维,如pd,超出了取值范围,那么,采用下式进一步调整:

3.3 算法步骤
本文提出的基于双层微粒群优化的机器人全局路径规划方法的步骤如下:
步骤1设定微粒群优化的参数取值;
步骤2随机初始化底层种群;
步骤3计算每个微粒的适应值,更新个体极值点Pbest和全局极值点Gbest;
步骤4由式(6)和(7)更新底层微粒;
步骤5判定路径与障碍物是否相交,若是,对微粒实施脱障操作;
步骤6判定底层微粒群优化是否满足终止条件,若否,转步骤3;
步骤7判定底层微粒群优化的运行次数是否满足要求,若否,转步骤2;
步骤8基于底层微粒群优化得到的最优路径,形成顶层微粒群优化的初始种群;
步骤9:计算每个微粒的适应值,更新个体极值点Pbest和全局极值点Gbest;
步骤10由式(6)和(8)更新顶层微粒;
步骤11判定路径与障碍物是否相交,若是,对微粒实施脱障操作;
步骤12判定顶层微粒群优化是否满足终止条件,若否,转步骤9;
步骤13输出全局最优路径,算法结束。
4 实验
为了验证本文方法的有效性,将其应用到含有密集障碍物环境的机器人路径规划中,并与仅含脱障操作的改进微粒群优化(Particle Swarm Optimization with Escape Obstacle Operator,EOO-PSO),以及标准微粒群优化(Standard Particle Swarm Optimization,SPSO)进行比较。
算法所需的参数设置如下:底层和顶层微粒群优化的微粒群规模N=20,维数D=10,最大迭代次数T=100。EOO-PSO、SPSO的参数设置同底层微粒群优化方法,但是,在EOO-PSO中利用了本文的脱障操作。实验的运行环境为Intel Celeron M-1.6 GHz CPU,504 MB RAM的PC机,以及MATLAB7.4。
机器人的移动环境如图3~5所示,在50 unit×50 unit的正方形环境中有12个静态障碍物,其顶点坐标已知,机器人的始点S和终点G的坐标已知。始点和终点任意改变3次,运行上述3种方法各30次,图3~5分别针对3种不同始终点的位置,给出3种方法得到的最好路径。表1列出相应的统计数据,由表1可知:
(1)对于相同的始终点位置,本文方法得到路径的性能指标均值最小,其次是EOO-PSO,最大的是SPSO。这说明,本文方法得到的路径具有最好的性能指标值,这体现在路径的长度短或者与障碍物相交的路段少,这是由于本文方法不但采用了双层微粒群优化,而且在每层还对不可行路径实施了脱障操作,而EOO-PSO仅对不可行路径实施了脱障操作,缺少双层微粒群优化,SPSO对不可行路径也没有实施脱障操作。通过可行解比例也可以看出,对不可行路径实施脱障操作是十分必要的。
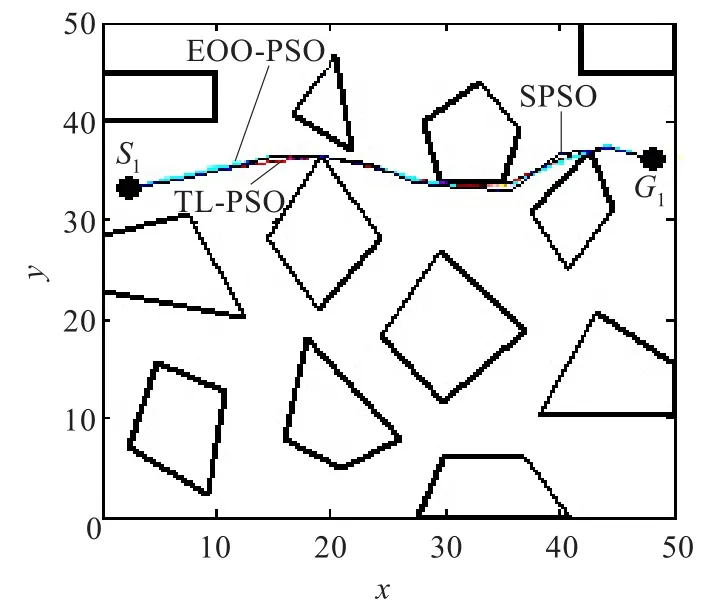
图3 始终点1不同算法所得最好结果
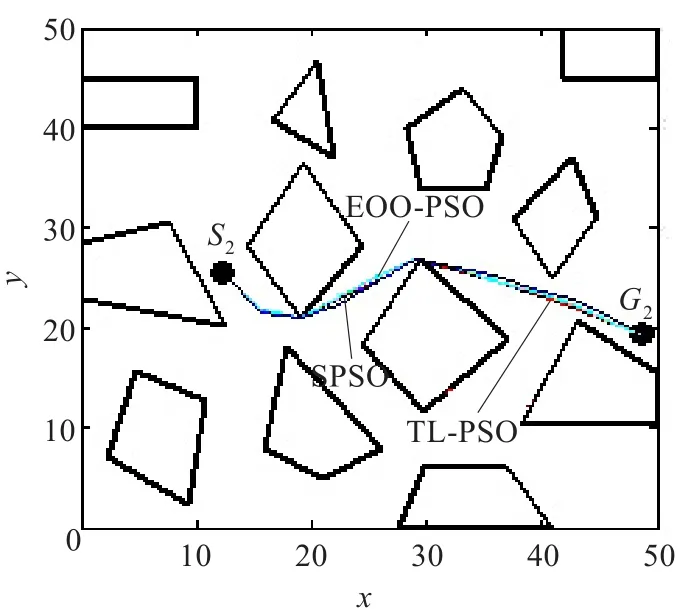
图4 始终点2不同算法所得最好结果
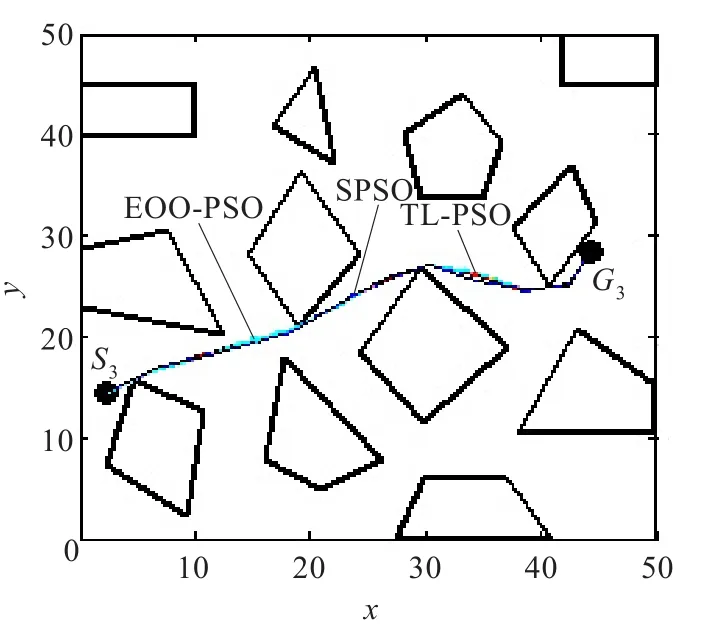
图5 始终点3不同算法所得最好结果
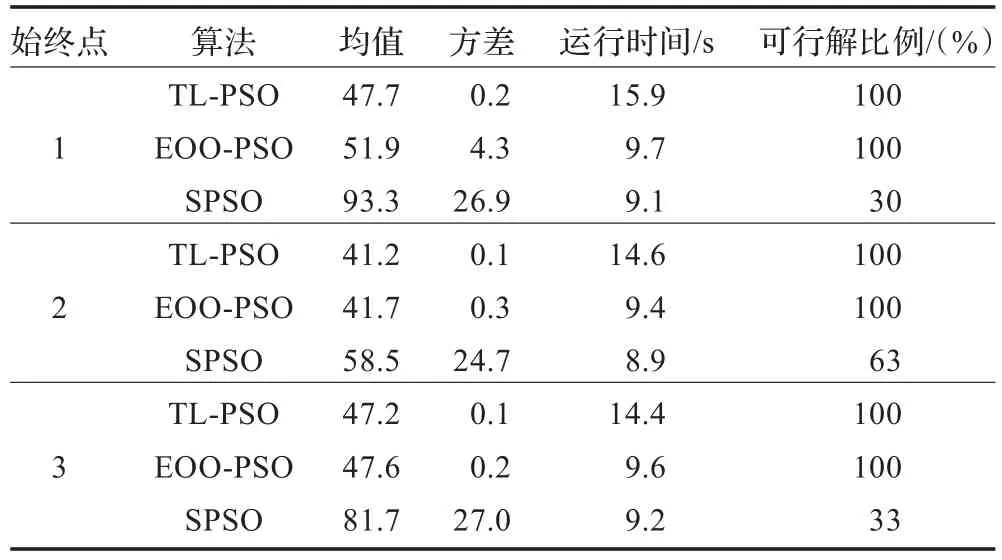
表1 不同算法得到路径的性能
(2)对于相同的始终点位置,本文方法得到路径的性能指标方差最小,其次是是EOO-PSO,最大的是SPSO,这说明,本文方法的稳定性优于EOO-PSO和SPSO。
(3)对于相同的始终点位置,优化机器人路径本文方法花费的时间最多,其次是EOO-PSO,最少的是SPSO,这是容易理解的,多花费的时间主要用于双层微粒群优化和脱障操作上。
上述实验结果表明,本文方法能够找到机器人的全局最优路径。
5 结论
针对微粒群优化用于密集障碍物环境机器人全局路径规划存在的问题,本文提出一种双层微粒群优化方法。该方法通过底层微粒群优化,得到若干最优路径;通过顶层微粒群优化,在这些最优路径附近局部搜索,从而得到机器人的全局最优路径;通过对不可行路径实施脱障操作,使其成为可行路径。三种场景的机器人路径规划结果表明,所提方法得到的路径均为可行路径,且性能指标优,算法的稳定性好。
[1]刘华军,杨静宇,陆建峰,等.移动机器人运动规划研究综述[J].中国工程科学,2006,8(1):85-94.
[2]Castillo O,Trujillo L,Melin P.Multiple objective genetic algorithms for path-planning optimization in autonomous mobile robots[J].Soft Computing,2007,11(3):269-279.
[3]谭冠政,贺欢,Sloman A.基于ACS算法的移动机器人实时全局最优路径规划[J].自动化学报,2007,33(3):279-285.
[4]李垒,叶涛,谭民,等.移动机器人技术研究现状与未来[J].机器人,2002,24(5):475-480.
[5]王志文,郭戈.移动机器人导航技术现状与展望[J].机器人,2003,25(5):470-474.
[6]张捍东,郑睿,岑豫皖.移动机器人路径规划技术的现状与展望[J].系统仿真学报,2005,17(2):439-443.
[7]Kennedy J,Eberhart R C.Particle swarm optimization[C]//Proc of IEEE Int Conf on Neural Networks.Piscataway,NJ:IEEE Press,1995:1942-1948.
[8]胡玉兰,姜明洋,赵慧静.基于改进粒子群优化算法的移动机器人路径规划方法研究[J].计算机工程与科学,2009,31(6):139-141.
[9]邓高峰,张雪萍,刘彦萍.一种障碍环境下机器人路径规划的蚁群粒子群优化算法[J].控制理论与应用,2009,26(8):879-883.
[10]孙波,陈卫东,席裕庚.基于粒子群优化算法的移动机器人全局路径规划[J].控制与决策,2005,20(9):1052-1060.
ZENG Xianfeng1,2,ZHANG Yong1
1.School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou,Jiangsu 221116,China
2.Electrical and Mechanical Engineering Branch of Xuzhou,Jiangsu Union Technical Institute,Xuzhou,Jiangsu 221011,China
Solving the problem of global robot path planning using Particle Swarm Optimization(PSO)has attracted various researchers in recent years,and fruitful achievements have been obtained.Previous studies,however,are hard to be applied to environments containing dense obstacles.Aiming at solving the problem of global robot path planning in environments containing dense obstacles,a two-layer PSO is presented.In this method,several optimal paths are first obtained using the bottom layer PSO.The globally optimal path is then got by local search near these optimal paths using the up layer PSO.In addition,an infeasible path becomes feasible by performing an escape obstacle operator.The proposed method is applied to solve the problem of robot path planning in various scenarios,and compared with previous methods.The experimental results confirm that the proposed method can find the globally optimal robot path.
robot;path planning;Particle Swarm Optimization(PSO);escape obstacle
采用微粒群优化解决机器人全局路径规划问题,近年来得到国内外学者广泛关注,并已经取得丰硕的研究成果。但是,已有成果往往难以应用于含有密集障碍物的环境。针对解决含有密集障碍物环境的机器人全局路径规划问题,提出一种双层微粒群优化方法。该方法通过底层微粒群优化,得到若干最优路径;通过顶层微粒群优化,在这些最优路径附近局部搜索,从而得到机器人的全局最优路径;通过对不可行路径实施脱障操作,使其成为可行路径。将所提方法应用于多场景的机器人路径规划,并与已有方法进行比较。实验结果表明,该方法能够找到机器人的全局最优路径。
机器人;路径规划;微粒群优化;脱障
A
TP242.6
10.3778/j.issn.1002-8331.1201-0059
ZENG Xianfeng,ZHANG Yong.Global robot path planning based on two-layer particle swarm optimization.Computer Engineering and Applications,2013,49(19):238-241.
国家自然科学基金(No.61005089);高等学校博士学科点专项科研基金资助课题(No.20100095120016)。
曾现峰(1972—),男,讲师,研究领域为智能优化与控制,机器人路径规划;张勇(1979—),男,博士,讲师,研究领域为智能优化与控制。E-mail:xianfeng669@126.com
2012-01-06
2012-03-01
1002-8331(2013)19-0238-04
CNKI出版日期:2012-06-01http://www.cnki.net/kcms/detail/11.2127.TP.20120601.1458.048.html
