一种新的k-medoids聚类算法

姚丽娟，罗可，孟颖

长沙理工大学计算机与通信工程学院，长沙 410114

一种新的k-medoids聚类算法

姚丽娟，罗可，孟颖

长沙理工大学计算机与通信工程学院，长沙 410114

1 引言

聚类是一个将数据集划分成若干组或类的过程，它使得同一个组内的数据对象具有较高的相似度，而不同组中数据对象则不相似，相似或不相似通常可利用距离进行度量。聚类已成为数据挖掘的一个重要研究领域[1]。

k-medoids算法[2-3]由于算法简单，收敛速度快及局部搜索能力强的优点被应用到了很多方面[4]。但是该算法依然存在对初值敏感，时间复杂度高，不适应大数据集和形状不规则的数据集等问题。而且该算法是基于梯度下降的[5-6]，因此，常常不可避免地使目标函数陷入局部极值，甚至会出现退化解和无解的情况。鉴于此，最近许多学者提出了很多改进的算法：文献[7-8]提出一个基于最小支撑树的聚类中心初始化方法，克服了Stephen J.Redmond给出的方法在估计密度方面的缺陷，但是增加了时间复杂度；文献[9]提出基于“metric access method”的方法，提高了聚类的正确率但也增加了额外的开销；文献[10]通过计算各个对象之间的距离选择初始中心点，并将中心点替换的范围局限于簇类，提高了算法的效率，但降低了聚类的正确率；文献[11]通过密度信息来产生初始中心，但它是以牺牲时间复杂度来换取较好的搜索性能，从而提高聚类效果；文献[12]采用基于核的自适应聚类，克服了k-medoids对初始值的敏感性问题，但是没有降低时间复杂度；文献[13]提出了将局部搜索过程嵌入到迭代局部搜索过程中的方法，显著减少了计算时间，但提高聚类效果没有得到提高。

上述文献中有些改进算法解决了初值敏感问题但时间复杂度却较高，有些能降低时间复杂度却对初值较较敏感，且都没有从实质上解决k-medoids算法聚类精度的问题，同时也没有解决高维数据集及形状不规则数据的聚类问题。

因此，本文提出一种能提高聚类精度的改进算法：（1）采用密度初始化，以克服k-medoids中存在的初值敏感问题；（2）基于密度的迭代搜索策略降低时间复杂度；（3）采用加权优化的准则函数进一步提高聚类精度。

2 k-medoids算法介绍及分析

典型的k-中心点算法描述如下：

输入：簇的数目k，包含n个对象的数据集。

输出：满足平方差最小的k个聚类中心及划分的k个聚类。

处理流程为：

步骤1从n个对象的数据集中随机选择k个对象作为初始的中心点；

步骤2指派每个剩余的对象给离它最近的中心点所代表的簇；

步骤3按照平方差函数值减少的原则，更新每个簇的中心点；

步骤4重复执行步骤2和步骤3，直到每个聚类不再发生变化为止。

平方差函数可以定义为：

其中，p为类Ci中的样本，Oj为聚类中心（p和Oj均是多维的）。

由于k-medoids聚类算法具有对初值敏感的缺点，不少学者提出基于密度思想的聚类[14]，具体表述如下。

取相隔距离较远的k个处于高密度区域的点作为中心点，则样本x的密度为：

Density(x)={p∈C|dist(x，p)≤r}（2）dist为某种距离度量，r为半径，C为样本集，公式（2）表示为以x为中心点，r为半径组成的球体所包含的样本数；其中r设定为r=u×θ，θ为用户给定常数，u为两两数据对象距离的均值，可以表述为：

密度初始化流程为：

（1）每个样本的密度计算出后，将密度大于平均密度的样本放于集合S，S表述为：

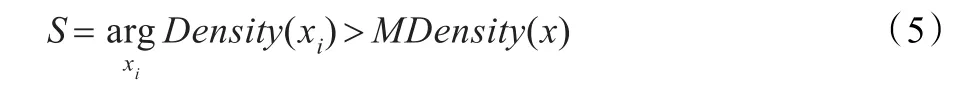
在S中取最大密度点作为第一个聚类中心Z1，并从S中删除：

公式（5）～（9）中变量i的取值均为1，2，…，n。

3 算法的改进思想

3.1 基于密度的迭代搜索策略

k-medoids算法因步骤3中心点的替代策略导致时间复杂度较高，计算代价也较大，因此很难适应到大数据和高维数据，为了解决这一问题，引入了一种基于密度的迭代搜索策略。该策略是在高密度区域内进行中心点的更新，即中心点的候选范围为最初的高密度区域。

在密度初始化流程中通过计算每个样本之间的距离来确定每个样本的密度，因此可以在此阶段实行一种机制：

（1）记录所有样本的欧氏距离矩阵（相似度矩阵），记为D；

（2）记录和初始中心点密度相近的k个矩阵，分别为M1，M2，…，Mk：

Mi={p∈S|dist(ki，p)≤MDensity}（10）公式（10）表示以ki为中心，MDensity为半径的点集，分别记为M1，M2，…，Mk，其中ki表示第i个中心点，S表示高密度点集。

每次迭代过程都在M1，M2，…，Mk个矩阵内进行，即每簇候选中心点优先在M1，M2，…，Mk个矩阵中选择，直到满足搜索条件为止；若都不满足，则考虑其他候选中心点。

因为密度相近的点很大程度上都属于同一聚类，且离最优中心点最近。这样的迭代过程避免了盲目地在所有样本中寻找最优中心点，这种改进策略很大程度上降低了时间复杂度。

相似度矩阵D的记录，也减少了k-medoids算法在划分簇时计算样本到簇中心距离的时间，而只需从D中查找相应样本的距离，从而减少计算时间。

3.2 准则函数优化

大多数聚类主要表现在：每类的内部距离应该尽量近，而各类之间的距离应该尽量远。但是一般算法都是将类内距离和最小作为准则函数，没有考虑到聚类总体质量是类内距离和类间距离共同决定的。基于这一思想，本文提出一种基于加权的准则函数作为k-medoids算法的目标函数，能有效地均衡类间距离和类内距离的不协调性。当基于加权的均衡化函数达到最小时，将得到最优的空间聚类结果。

类间距离b(c)定义为不同聚类中心点间的距离，可以表述为：

基于加权优化的准则函数采用类内距离和类间距离共同决定，则准则函数可以表示为：

其中，w1、w2为加权系数，且w1+w2=1；w1、w2加权系数设定的目的是：对于那些聚类效果不明显、数据形状不规则的数据集，必须在w1、w2达到某种关系的情况下，聚类效果才达到最好。

3.3 新算法描述

下面给出新算法的主要步骤：

输入：包含n个数据对象的样本数据库，参数k，θ，w1，w2值；

输出：k个聚类中心及最优聚类。

步骤1选择、优化初始中心并做初步聚类划分：

（1）根据相似度矩阵D和密度初始化方法找出k个初始中心点，并记录M1，M2，…，Mk；

（2）根据当前的中心点对其他对象进行初始聚类划分。

步骤2执行基于密度的迭代过程：

步骤3输出最终的k个中心点及聚类划分。

3.4 算法分析

本文算法采用密度初始化方法找到接近最终聚类中心的初始中心点，之后的迭代过程就可以简化；同样考虑每个聚类中心往往都是处于高密度区域，在迭代过程中中心点的替换范围可以限制在与初始中心点密度相近的高密度区域之内，则迭代次数明显降低，在大数据集上尤为明显。采用加权优化的准则函数判断聚类是否达到收敛，进一步提高聚类的准确率。

在时间复杂度方面，起决定作用的是步骤2，在这个阶段，新算法进行k次搜索的范围是不同的。对于在数据分布均匀的情况下，可以确定每个中心点候选范围在[2，(n-k)/k]内，再根据公式（4）的计算，可以缩小范围，则表示为[2，d1/k](d1≪n-k)。根据算法流程，在进行第i(i=1，2，…，k)轮替换时，此时中心点候选范围Mi中数据点的数量最大为d1/k个。在中心点替换过程中，对其余n-k个数据对象进行划分，需进行k次，所以时间复杂度为O(d1×(n-k))。而根据步骤2，整个替换过程需要进行k次，则总的时间复杂度可以为O(k×d1×(n-k))，由于d1≪n-k，所以时间复杂度可以表述为O(k(n-k))，与传统k-medoids算法的时间复杂度O(k(n-k)2)相比，小一个数量级，明显降低了时间复杂度。

3.5 参数分析

聚类的一个难点是算法要适应各种情况，聚类参数则是根据实验和经验来进行确定，参数θ的经验值一般为0＜θ＜1。

MDensity参数体现了候选解范围的大小，过大会因为迭代次数较多导致时间复杂度高，而过小会因为收敛较快导致聚类精度较低。因此，MDensity参数需要根据实际样本的平均密度进行计算得到。

w1、w2对于数据形状规则的数据集一般相差不大，几乎都接近0.5。但是对于形状不规则的数据，w1、w2体现了数据集的不规则程度，且影响准则函数E的大小，最终决定了聚类的准确率。因此，根据不同的数据集需要设置不同的w1、w2，但w1、w2必须满足w1+w2=1的关系，使聚类效果达到最好并能提高算法的适应性。

4 算法仿真与性能分析

为了检验该算法的有效性，采用传统的k-medoids算法及部分改进算法与本文算法进行实验对比，且在聚类效果和算法收敛时间两方面进行比较。

仿真环境：操作系统Windows 7，编译软件Matlab7.0.1；Pentium®Dual-Core CPU T4200@2.00 GHz，内存为2 GB。

（1）样本数据：下面给出一个样本数据库（如表1），并对它实施本文改进的k-medoids算法。

表1中有24个样本对象，为了表现样本数据库的空间效果，把表中的属性对应到坐标轴上，如图1所示。为了验证加权准则函数的高效性，图3给出了各个准则函数的趋势图说明w(c)、b(c)与加权准则函数之间的关系。按照改进的算法，当k=4时，加权准则函数值最小E=28.23，且w(c)=18.12，b(c)=34.17。图2给出当k=4时聚类的结果，m0、m1、m2、m3分别为各类的中心点，与样本数据库的最优结果相吻合。

分析：当k=4时，加权准则函数值最小，其中准则函数由类内距离和类间距离两部分组成，且与类间距离和类内距离保持一定关系。图3给出加权准则函数和类间距离、类内距离的趋势图。加权准则函数最小值对应的k值为4，即样本数据库的最优聚类数目，其中类内距离随着k值的增大呈下降趋势。在该实验中k越大，类的数目就越多，类所含的样本对象数目就越少，影响也随之减小，因此类间距离是呈下降趋势的，并且在k值比较小的情况下，其变化速度比较快。而类间距离随着k值的增大呈上升趋势，并且当k等于样本个数时，类间距离达到最大，因为这时每个对象都是一个类，类内距离已经为零。而加权准则函数均衡了类内距离和类间距离对样本对象造成的影响，符合最优聚类的结果。

表1 样本数据库

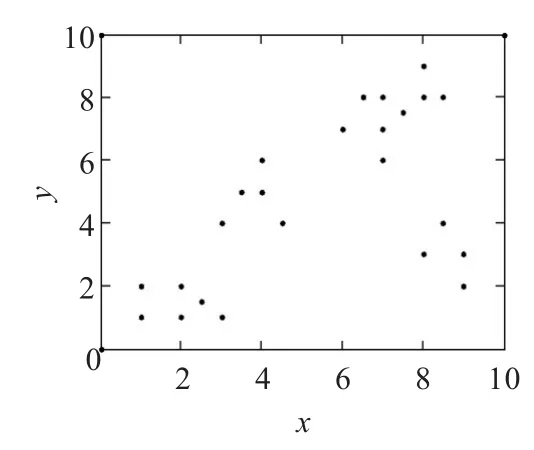
图1 样本数据

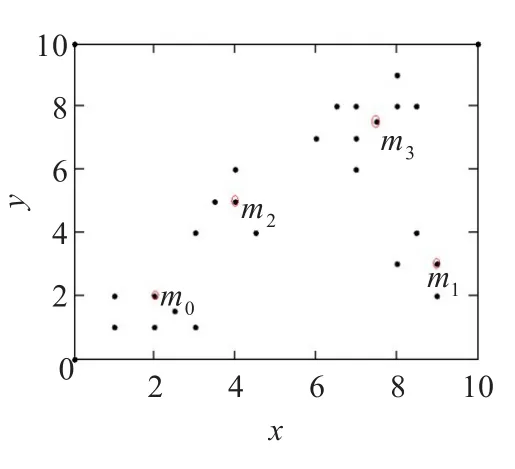
图2 k=4时的样本聚类图

图4表示样本数据库中，在k=4的情况下不同算法准则函数的收敛时间图。从图中可以看出，在开始的时候，本文算法的加权准则函数E值均比其他算法采用的准则函数都要小，说明采用密度初始化中心点效果明显，此时的中心点离最终的中心点较近。随着聚类迭代的推进，E加权准则函数在0.4 s就已经收敛，达到最终的聚类，说明采用基于密度迭代的搜索策略能减少聚类时间和迭代次数并有效聚类。而其余三种算法均采用随机初始中心，因此最初准则函数值较大，IKMD算法采用在各簇内选择候选中心点，一定程度上也减少了算法收敛时间。算法2[15]采用增量式的思想扩大搜索范围，效果比IKMD算法好，但是相比于本文算法，收敛时间还是较长。

图4 各算法聚类收敛图

（2）标准数据集：Iris、Wine及Breast Cancer数据集，每类数据集介绍如表2所示。

表2 各数据集的参数比较

在上述三个数据集中，Iris、Wine及Breast Cancer（BC）的数据类型为区间标度变量，用欧氏距离度量数据库中对象之间的相异度。

通过30实验，本文提到的用户自定义参数设置如下则效果最好：

本文算法和原始k-medoids、部分改进算法及k-means的改进算法进行比较，结果如表3～表5。

表3 各算法在Iris数据集的正确率和收敛时间比较

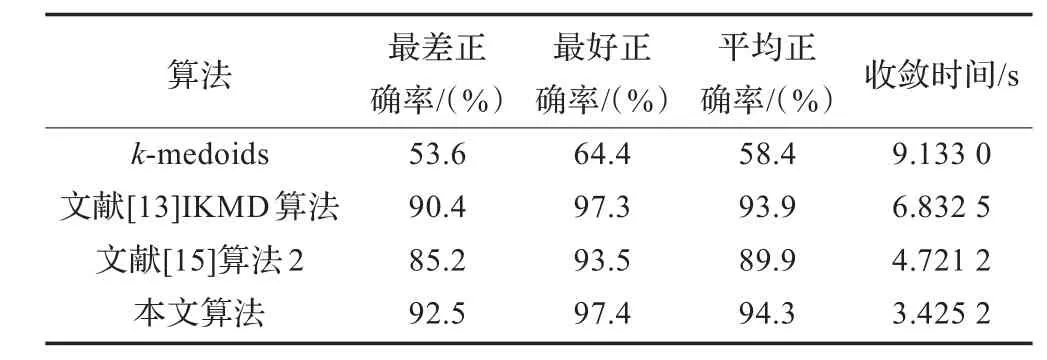
表4 各算法在Wine数据集的正确率和收敛时间比较

表5 各算法在Breast Cancer数据集的正确率和收敛时间比较

从表3、表4和表5可以看出，三种不同类型的数据集，聚类正确率及收敛时间都有所提高。Iris和Wine数据集最好正确率都达到97%以上，且多次实验的结果都比较平稳，波动范围几乎都控制在5%以内，聚类效果较好。在BC数据集中收敛时间大幅度减少，远远小于IKMD算法和算法2的收敛时间，并提高了正确率。

综上所述，在同样的实验条件下，针对不同的数据集，本文算法既能保证聚类性能又能大幅度提高算法效率；对于不同形状的数据集具有较好的适应性；对数据集中的噪音数据具有较好的抗干扰能力，聚类效果较稳定。上述实验结果验证了本文算法的可行性和有效性，并能适应多维大数据集。

5 结束语

提出一种新k-medoids聚类算法，在分析聚类特性的基础上给出基于加权的准则函数，与传统评价函数不同，该函数对类内和类间差异进行有效权衡，使得算法的有效性得到充分的发挥；同时在中心点替换过程中采用基于密度迭代的搜索策略，很大程度上降低了算法的计算量。本文算法输入的参数较少，时间复杂度低，能对任何形状、不同分布特性、不同密度、不同大小的数据进行聚类。与k-medoids算法及其相关改进算法相比，本文算法具有较强的适应性，适合大规模的数据集，且执行效率较高，聚类结果稳定。但是本文算法还存在以下问题：（1）w1、w2参数能否自适应给出；（2）算法能实现k值自动确定，但是在大数据集的情况下本文算法没有讨论。这将是下一步的研究重点。

[1]Han Jiawei，Kamber M.数据挖掘：概念与技术[M].范明，译.北京：机械工业出版社，2007-03.

[2]Chen Xinquan，Peng Hong，Hu Jingsong.K-medoids subatitution clustering method and a new clustering validity index method[C]// Proc of 6th World Congress on Intelligent Control and Automation，2006：5896-5900.

[3]任晓东，张永奎，薛晓飞.基于K-Mode聚类的自适应话题追踪技术[J].计算机工程，2009，35（9）：222-224.

[4]Mishra N，Motwani R.Optimal time bounds for approximata clustering[J].Machine Learning，2004，56：35-60.

[5]Ben-David S.A k-median algorithm with running time independent of data size[J].Machine Learning，2004，56：61-87.

[6]Har-Peled S，Kushal A.Smaller coresets for k-median and k-means clustering[J].Discrete Comput Geom，2007，37：3-19.

[7]李春生，王耀南.聚类中心初始化的新方法[J].控制理论与应用，2010，27（10）：1436-1440.

[8]Gao Danyang，Yang Bingru.An impronved K-medoids clustering algorithm[C]//Proc of the 2nd International Conference on Computer and Autonmation Engineering（ICCAE），2010：132-135.

[9]Barioni C N M，Razente H L，Traina A J M，et al.Acceleration K-medoids-based algorithms through metric access method[J]. Jourmal of Systerm and Software，2008，81（3）：343-355.

[10]Park H S，Jun C H.A simple and fast algorithm for k-medoids clusting[J].Expert Systerm with Applications，2009，36（2）：3336-3341.

[11]Pardeshi B，Toshniwal D.Improved K-medoids clustering based on cluster validity index and object density[C]//Proc of the 2ndIEEEInternational AdvanceComputingConference，2010：379-384.

[12]孙胜，王元珍.基于核的自适应k-medoid聚类[J].计算机工程与设计，2009，30（3）：674-677.

[13]吴景岚，朱文兴.基于k中心点的迭代局部搜索聚类算法[J].计算机研究与发展，2004，41：246-252.

[14]孙秀娟，刘希玉.基于初始中心优化的遗传k-means聚类新算法[J].计算机工程与应用，2008，44（23）：166-168.

[15]夏宁霞，苏一丹，谭希.一种高效的k-medoids聚类算法[J].计算机应用研究，2010，27（12）：4517-4519.

YAO Lijuan,LUO Ke,MENG Ying

Institute of Computer and Communication Engineering,Changsha University of Sciences and Technology,Changsha 410114,China

For the disadvantages that sensitivity to centers initialization,lower clustering accuracy and slow convergent speed ofk-medoids algorithm,a novelk-medoids algorithm based on density initialization,density of iterative search strategy and optimization criterion function is proposed.The Initialization of the algorithm is that,it chooses k cluster centers in the high-density area which are far apart,effectively positioning of the final cluster center.To replace the centers are in the ranges which are proximity to thek-initial centers,to reduce the scope of the search candidate point.Criterion function of equalization based on class density and within-class density weighted is adopted to improve the clustering precision.Experimental results show that this algorithm can improve the clustering quality,shorten the clustering time compared with traditionalk-medoids algorithms or other improved algorithms.

clustering;k-medoids algorithm;density initialization;criterion function

针对k-medoids算法对初始聚类中心敏感，聚类精度较低及收敛速度缓慢的缺点，提出一种基于密度初始化、密度迭代的搜索策略和准则函数优化的方法。该算法初始化是在高密度区域内选择k个相对距离较远的样本作为聚类初始中心，有效定位聚类的最终中心点；在k个与初始中心点密度相近的区域内进行中心点替换，以减少候选点的搜索范围；采用类间距和类内距加权的均衡化准则函数，提高聚类精度。实验结果表明，相对于传统的k-mediods算法及某些改进算法，该算法可以提高聚类质量，有效缩短聚类时间。

聚类；k-medoids算法；密度初始化；目标函数

A

TP391.4

10.3778/j.issn.1002-8331.1112-0644

YAO Lijuan,LUO Ke,MENG Ying.New k-medoids clustering algorithm.Computer Engineering and Applications, 2013,49（19）：153-157.

国家自然科学基金（No.11171095，No.10871031）；湖南省自然科学衡阳联合基金（No.10JJ8008）；湖南省教育厅重点项目（No.10A015）；湖南省科技计划项目（No.2011FJ3051）。

姚丽娟（1986—），女，硕士，主要研究方向为数据挖掘，计算机应用；罗可（1961—），男，博士，教授，研究方向为数据挖掘，计算机应用等；孟颖（1984—），女，硕士，主要研究方向为数据挖掘，计算机应用。E-mail：yaolijuan1986@163.com

2012-01-11

2012-03-26

1002-8331（2013）19-0153-05

CNKI出版日期：2012-05-22http://www.cnki.net/kcms/detail/11.2127.TP.20120522.1316.012.html