4类图完美匹配数目的显式表达式

唐保祥，任韩

1.天水师范学院数学与统计学院，甘肃天水 741001

2.华东师范大学数学系，上海 200062

4类图完美匹配数目的显式表达式

唐保祥1，任韩2

1.天水师范学院数学与统计学院，甘肃天水 741001

2.华东师范大学数学系，上海 200062

1 引言

匹配计数理论是图论研究的重要内容之一，在过去的几十年中，它是快速发展的组合论中许多重要思想的源泉，其研究成果已经在多个领域得到应用[1-5]。此问题引起一些学者的广泛研究，也得到了许多特殊图类完美匹配的计数公式[6-13]。遗憾的是，Valiant证明了一个图（即使是偶图）的完美匹配计数是NP-难问题[5]。因此，不存在计算图的完美匹配图数目的一般方法，要得到一个图的完美匹配的数目是很困难的。文献[14-18]用划分、求和、再递推的方法给出了一些图类完美匹配的计数公式。本文在此基础上，使用了嵌套递推的方法给出了4类新图的完美匹配数目的计算公式，本文方法适合相同结构重复出现的，结构比较复杂的图类完美匹配数的求解。

定义1若图G的两个完美匹配M1和M2中有一条边不同，则称M1和M2是G的两个不同的完美匹配。

定义2两条长为n的路为P1=u1u2…un+1，P1=ν1ν2…νn+1，分别连接路P1与P2的顶点ui与νi(i=1,2,…,n+1)所得到的图，称为长为n的梯子，记为Tn。

2 结果及其证明

图12 -nDC4图

图2 G1图

图32 -nW6图

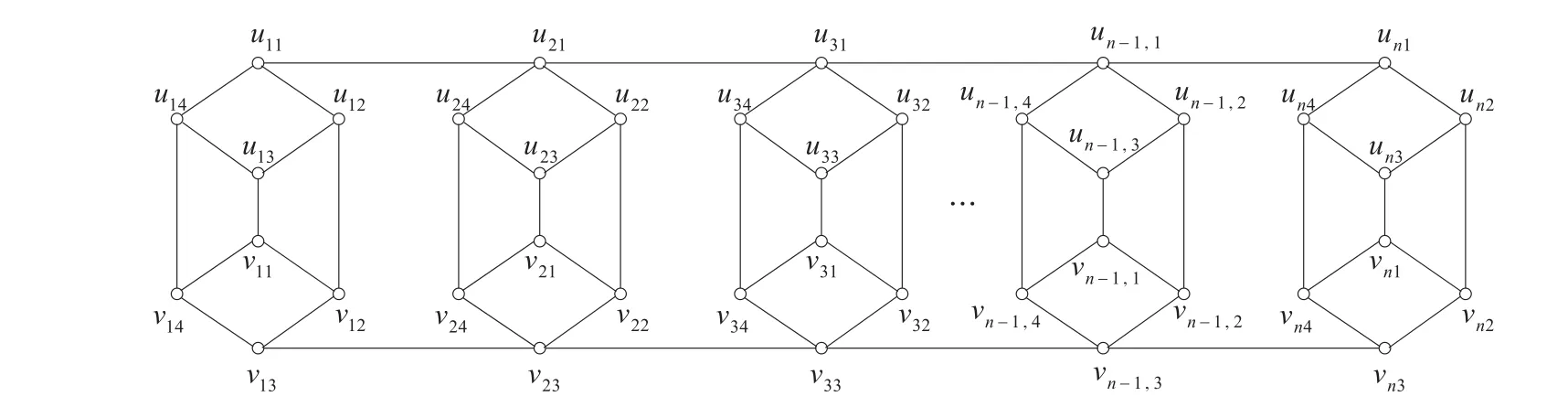
图42 -2nDC4图

图52 -nT4图

证明为了求σ(n)，先定义2个图G2和G3，并求其完美匹配的数目。将长为1的路u1u2的端点u1和u2分别与图2-nT4的顶点u12和u13，u13和u14各连接一条边，得到的图分别记为G2和G3，如图6和7所示。易知图G2和G3均有完美匹配；β(n)和γ(n)分别表示图G2和G3的完美匹配的数目，显然G2≅G3，所以β(n)=γ(n)。

图6 G2图

图7 G3图

3 结论

图的完美匹配计数是图论和组合数学中的一个重要课题，有着广泛的应用前景。Lovász L和lummer M曾提出完美匹配计数的一个猜想：任何2-边连通3-正则图都有指数多个完美匹配。本文结论验证了Lovász L和Plummer M猜想在这4类图上的正确性。本文方法是求解许多特殊图类完美匹配数目的有效方法，用此方法还可以求出一些图的所有Hamilton圈的数目[14]。

[1]Pauling L.The nature of chemical bond[M].New York：Cornell University Press，1939.

[2]Kasteleyn P W.Graph theory and crystal physics[M]//Harary F.Graph Theory and Theoretical Physics.London：Academic Press，1967：43-110.

[3]Hall G G.A graphic model of a class of molecules[J].Int J Math Edu Sci Technol，1973，4（3）：233-240.

[4]Swinborne-Sheldrake R，Herndon W C，Gutman T.Kekule structures and resonance energies of benzennoid hydrocarbons[M]// Tetrahedron Lett.Oxford：Pergamon-Elsevier Science Ltd，1975：755-758.

[5]Valiant L G.The complexity of computing the permanent[J]. Theoretical Compute Science，1979，8（2）：189-201.

[6]Lovász L，Plummer M.Matching theory[M].New York：North-Holland Press，1986.

[7]张福基，陈荣斯.六角系统克库勒结构的计数[J].新疆大学学报：自然科学版，1986，3（3）：10-14.

[8]张福基，陈治柏.广义渺位苯图的完美匹配数的计算[J].新疆大学学报：自然科学版，1986，3（3）：6-10.

[9]Zhang Heping.The connectivity of Z-transformation graphs of perfect matchings of polyominoes[J].Discrete Mathematics，1996，158：257-272.

[10]Zhang Heping，Zhang Fuji.Perfect matchings of polyomino graphs[J].Graphs and Combinatorics，1997，13：259-304.

[11]Yan Weigen，Zhang Fuji.Enumeration of perfect matchings of a type of Cartesian products of graphs[J].Discrete Applied Mathematics，2006，154：145-157.

[12]王洪伟.二部图匹配强迫数的谱[J].山东大学学报：理学版，2009，44（12）：30-35.

[13]江蓉，王守中，任海珍.两类2-共振的六角系统的刻画[J].河北大学学报：自然科学版，2009，29（4）：342-350.

[14]唐保祥，任韩.几类图完美匹配的数目[J].南京师大学报：自然科学版，2010，33（3）：1-6.

[15]唐保祥，李刚，任韩.3类图完美匹配的数目[J].浙江大学学报：理学版，2011，38（4）：16-19.

[16]唐保祥，任韩.2类图完美匹配的数目[J].西南师范大学学报，自然科学版，2011，36（5）：16-21.

[17]唐保祥，任韩.3类图完美匹配的计数[J].南京师大学报：自然科学版，2012，35（1）：16-21.

[18]唐保祥，任韩.6类图完美匹配的数目[J].中山大学学报：自然科学版，2012，51（2）：40-44.

TANG Baoxiang1,REN Han2

1.School of Mathematics and Statistics,Tianshui Normal University,Tianshui,Gansu 741001,China
2.Department of Mathematics,East China Normal University,Shanghai 200062,China

Matching counting theory is at the core of graph theory,since it is origins from both physics,computer science and chemistry.But the problem of counting the number of perfect matching for general graphs is NP-hard.By applying differentiation,summation and re-nested recursive calculation,several counting formulas of the perfect matching for four specific types of graphs are given.By the presented method,the number of all perfect matching of many graphs that the same structure is repeated can be calculated.

perfect matching;linear recurrence relation;characteristic equation

匹配计数理论是图论的核心内容之一，此问题有很强的物理学、计算机科学和化学背景；但是，一般图的完美匹配计数问题却是NP-难问题。用划分、求和、再嵌套递推的方法给出了4类图完美匹配数目的显式表达式；所给出的方法，可以计算出相同结构重复出现的许多图的所有完美匹配的数目。

完美匹配；线性递推式；特征方程

A

O157.5

10.3778/j.issn.1002-8331.1206-0203

TANG Baoxiang,REN Han.Explicit formulae for number of perfect matching in four types of graphs.Computer Engineering and Applications,2013,49（19）：44-48.

国家自然科学基金（No.11171114）。

唐保祥（1961—），男，副教授，研究方向：图论和组合数学。E-mail：tbx0618@sina.com

2012-06-12

2012-08-10

1002-8331（2013）19-0044-05

CNKI出版日期：2012-09-25http://www.cnki.net/kcms/detail/11.2127.TP.20120925.1000.028.html