非结构网格自适应细化的实现与应用❋

李于锋

（中国工程物理研究院 计算机应用研究所，四川 绵阳 621900）

0 引言

在工程数值模拟领域，针对复杂结构的有限元计算应用十分广泛。在机械零件制造中如何高效得到结构关键点的应力，以及在流场中如何快速准确地捕捉激波等问题，若单纯依靠不断全局细化的网格增加计算量，是不经济的。网格自适应技术兼顾了计算精确性和计算效率，能够使用较少的网格计算代价获得较为准确的计算结果［1］。

自适应网格技术在国外发展十分迅速，在成熟的商业软件中都有功能体现，如LS－Dyna的重划分网格的自适应实现等；在美国Sandia实验室开发的多物理耦合计算框架SIERRA［2］中，也实现了H自适应的策略。在国内，北京应用物理与计算数学研究所开发的JASMIN［3］结构化网格自适应框架已经在多个应用程序中得到实际应用。中科院科学与工程计算国家重点实验室开发的PHG［4］能够对四面体网格进行自适应细化。然而涵盖二维和三维非结构化网格自适应的软件模块还相对缺乏，本文采取基于拼片修复的误差估计方法，尝试在自主研发的有限元计算框架中实现二维三角形网格和三维四面体网格的自适应细化，在多层细化中考虑网格质量，并用算例验证该方法的有效性。

1 后验误差估计

后验误差估计是通过对有限元计算结果进行再处理以提高计算精度的后验方法，这种过程称为修复。修复解更接近精确解，以此作为标准衡量有限元解的误差的方法称为后验误差估计。误差定义为精确解和近似解的差，对于位移u，定义为：

其中：L为线性微分算子，p为已知函数。

定义能量范数为：

其中：D为弹性矩阵；S为应变关于位移的算子。由算子S定义的应变和应力分别为：

将式（1）代入式（4），联立式（5）、式（6），能量范数也可以写为：

误差能量范数中的真实应力是未知的，采用超收敛的拼片修复（Superconvergent Patch Recovery）［5，6］方法获得较准确的应力或应变，来对有限元近似解进行衡量。

2 三角形网格细化策略及实现

为了保持网格质量，二维三角形网格的自适应细化采取互连三个边中点将单元一分为四的正则细化方案。在细化单元和非细化单元之间会产生过渡单元，这些单元的一条边或者两条边被细化。一个单元在细化过程中可能被标识细化边的情形如图1所示。

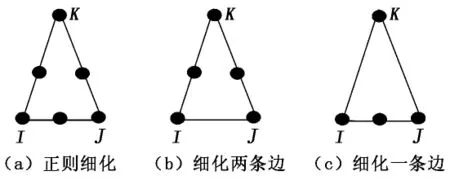
图1 三角形可能的细化情况

图1（a）为正则细化情形，将三条边的中点互连即可将原单元一分为四；图1（c）的单元只有一条边被细化，直接将细化边中点与相对的顶点连接，可将单元一分为二；图1（b）的单元有两条边被细化，此类单元细化要考虑质量问题，细化方式有如图2所示的两种选择。经过简单计算，就可以选择较好的细分方式。

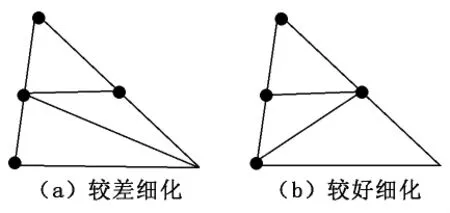
图2 过渡单元的质量控制

三角形网格经过多次细化后，一个单元可能会产生多次非正则细化情形，从而导致较差的网格质量，为了保证多层细化之后，网格质量不至于太差，需要对细化过程进行一定的约束控制。为此设定一个规则：若将被细化单元本身不是正则细化而得到的，则返回到该单元的父单元，进行正则细化后，再细化该单元（可能是正则或非正则细化）。该准则控制网格质量在实际中取得较好效果，如图3所示。

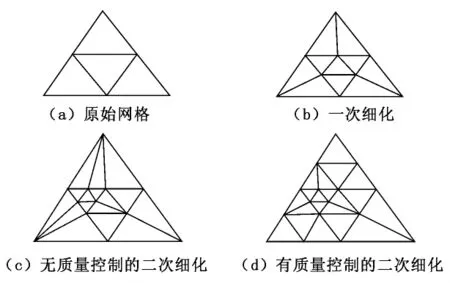
图3 三角形网格细化的质量控制

3 四面体网格细化策略及实现

三维四面体网格由于对复杂几何模型更容易逼近，在工程实际的建模中应用广泛。然而四面体网格的细化由于维度的增加，比三角形的细化算法更加复杂。首先，若选择每条边细化的完全细化方式，可以将单元一分为八（见图4），四个顶点处形成4个四面体外，内部还可剖分形成4个四面体，然而内部的小四面体并不能保证质量，由于网格协调性的约束，导致过渡网格的剖分情形复杂而且质量更差。为此，本文采取二分法作为四面体的细分方案。二分法实现简单，一次细化只需添加一个新节点，也不至于产生过多的单元，见图5。

图4 四面体的八分细化 图5 四面体的二分细化

为了在程序中实现二分细化，根据网格几何协调性总结出了三种细化方法，分别是边细化法、逐单元细化法和细化边列表法。边细化法是被标细化单元全部细化最长边，若某单元有多个边被细化的，则按照边的长度进行顺序二分。该方法的缺点是一次细化将导致某单元多次细化，网格质量很差。逐单元细化法是被标识细化单元即时细化最长边，但若由于邻居细化已经细化了，则此次就不再继续细化它的子树，该方法导致短边细化的情形较多且质量不好。细化边列表法是将所有被标识待细化单元的最长边存入一优先队列，按照长度递减排序，遍历该细化边列表，对每个细化边，即时细化该边所在的单元，为了不至于产生过多的细化，将引起该边被细化的单元记为该细化边的主单元，若遍历细化边列表时，该边的主单元（可能有多个）都已经被细化，则跳过该细化边。经改进后的细化边列表法能在实际算例中表现出网格质量的极大改善。

4 自适应网格实例分析

4.1 L形结构板的应力分析

经典的L形结构的物理模型如图6（a）所示，顶部和右侧为滑移边界，左侧受均布拉力，材料为弹性。该结构在L的拐角处容易产生应力集中，自适应细化的网格很好地展示了该问题，用较少的网格量达到了较为精确的解，相对能量范数误差从初始网格的24%下降到最终自适应网格的4%，初始网格和自适应网格分别见图6（b）和图6（c）。

4.2 带孔板的拉伸分析

无限大的平面板受单向拉伸的物理模型如图7（a）所示，利用对称性和圣维南原理，模拟计算其四分之一的原始网格见图7（b），经过两次自适应细化之后的网格见图7（c），相对能量范数误差从原始的10%降到4%。

4.3 三维悬臂短梁的应力分析

悬臂短梁受顶端均布压力的物理模型如图8（a）所示，原始四面体网格见图8（b），采用质量控制后的自适应网格见图8（c），相对能量范数误差从45%下降 到7%。

图6 L形结构的应力分析

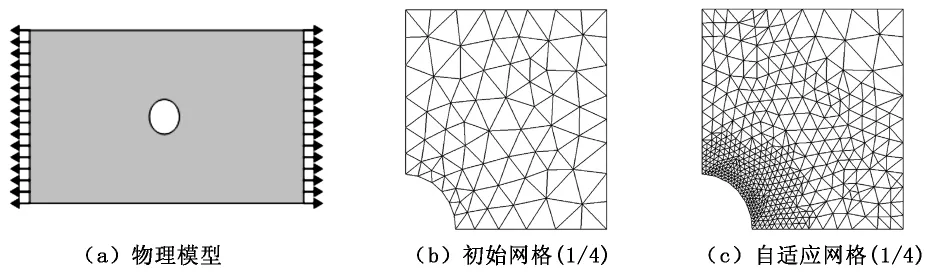
图7 平板拉伸分析

图8 三维悬臂短梁应力分析

5 结论

在大尺度复杂结构的有限元模拟中，非结构网格自适应是一种关键技术，它能够在保证精度的前提下，大大缩减计算代价。本文算例中的自适应网格细化能仅在增加局部细化工作量的情况下，获得较好的模拟效果，表明了非结构网格自适应算法的正确性和有效性。

［1］Zienkiewicz O C，Taylor R L，Zhu J Z.The finite element method：Its basis and fundamentals ［M］.6th ed.England：Elsevier Ltd，2005：456－524.

［2］Stewart J R，Edwards H C.A framework approach for developing parallel adaptive multiphysics applications［J］.Finite Elements in Analysis and Design，2004，40：1599－1617.

［3］Mo Zeyao，Zhang Aiqing，Cao Xiaolin，et al.JASMIN：aparallel software infrastructure for scientific computing［J］.Front Comput Sci China，2010，4（4）：480－488.

［4］Zhang Linbo.PHG：A toolbox for developing parallel adaptive finite element programs ［J］.Bulletin of the Chinese Academy of Sciences，2011，25（4）：298－300.

［5］Zienkiewicz O C，Zhu J Z.Superconvergent patch recovery and a posteriori error estimation in the finite element method，Part 1：A general superconvergent recovery technique［J］.Internat J Num Meth Eng，1992，33：1331－1364.

［6］Zienkiewicz O C，Zhu J Z.The superconvergent patch recovery（SPR）and a posteriori error estimates，Part 2：Error estimates and adaptivity［J］.Internat J Num Meth Eng，1992，33：1365－1382.