鼠笼式感应风力发电系统的优化控制

王 武

(许昌学院 电气信息工程学院，河南 许昌461000)

0 引 言

随着世界经济的不断发展和国际工业化进程的逐步加快，全世界能源需求持续增加。为了缓解能源危机，保护自然环境，可再生能源的开发利用逐渐提上人类可持续发展的日程。风力发电清洁无污染，施工周期短，投资灵活，占地少，具有较好的经济效益和社会效益，风力发电技术已成为全世界竞相开发的重要新能源技术［1］。风力发电技术是涉及空气动力学、自动控制、机械传动、电机学等多学科的综合性高技术系统工程。国内对风电机组系统设计技术的研究起步不久，风电机组的大型化、变桨距控制、变速恒频等先进风电技术还远未解决，致使我国大型风力机几乎全部为进口产品。因此，深入研究风力发电机组系统设计技术对于开发风能和实现风电机组国产化具有重要理论意义和工程应用价值。目前，风力发电机组的研究难点是风电机组大功率、高可靠性、高效率、低成本。为攻克这些难点，国内外的研究热点是系统优化设计和先进控制策略［2］。由于所受工况瞬态多变且工作环境恶劣，空气动力学的不确定性和电力电子功率变换装置模型的复杂性，系统模型不易确定，风力发电机组是一个复杂、多变量、非线性的不确定系统，因此，系统建模分析是风力发电机系统设计的关键［3］。文献［4］建立了风能转换系统的机理模型，并得到线性参数变化系统模型，设计了基于LPV 模型的增益调度控制器，实现了节距角和电磁转矩的动态补偿。文献［5］提出变桨距风电系统功率控制的逆系统鲁棒方法，可以在风速任意波动条件下有效地控制风电系统的输出功率，并且对系统参数的大范围扰动具有较强的鲁棒性。文献［6］开发了基于无源性的双馈风力发电机控制系统，能够高速、有效实现最大风能捕获，同时对电机参数摄动及负载转矩变化具有很强的鲁棒性。文献［7］为了实现额定风速以下风能转换系统风能捕获率的最大化，根据风速的多时间尺度特性，基于频率分离原理建立了风能转换系统的双频环模型。并针对低频环和高频环分设优化控制器，实现了风能转换系统双频环滑模控制，实现了风能捕获率最大化。

鼠笼式异步电机风力发电系统包括恒速运行的失速型风力发电系统以及由鼠笼异步电机和背靠背的四象限变流器组成的变速恒频风力发电系统，该系统存在齿轮箱、传动轴这一脆弱环节，在频繁的转矩冲击和大幅度波动下容易损坏。国内、外虽然大量开发直驱式风力发电系统以提高效率和可靠性，但已装机的感应风力发电系统还未退出历史舞台，研究以鼠笼式异步电机作为发电机的风力发电系统中传动链的受冲击情况以及以减少转矩冲击、提高风能利用率的控制方法，可以改善其控制品质，同时对其他风电系统控制具有一定的借鉴和指导意义。本文以鼠笼式感应发电机为对象构建大功率变速定桨距风能转换电磁子系统，结合风力机空气动力学模型的分析和建模，给出了传动装置模型和鼠笼式感应电机模型，并结合MATLAB/Simulink 软件实现了系统的控制策略，通 过系统仿真说明风力发电系统的最优控制特性跟踪。

1 基于笼型感应电机风力发电系统数学模型

基于笼型感应电机的风力发电系统可以将捕获的气流能量转换成电能的装置，包含四个子系统构成，空气动力子系统(AS)、机械传动链子系统(DT)、电磁子系统(EMS)和电网界面，典型的定速变桨距风能转换系统框图如图1 所示［8］。

1.1 空气动力子系统建模

风力机的叶尖速度比表示叶片速度与风速之比:

式中:R 是叶片长度;Ω1是风轮角速度;υ 是风速。

功率系数Cp表示风力机的风能利用效率，风力机的捕获功率可表示为:

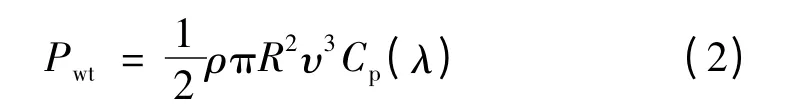
式中，ρ 为空气密度。

转矩系数CΓ，可表示为:

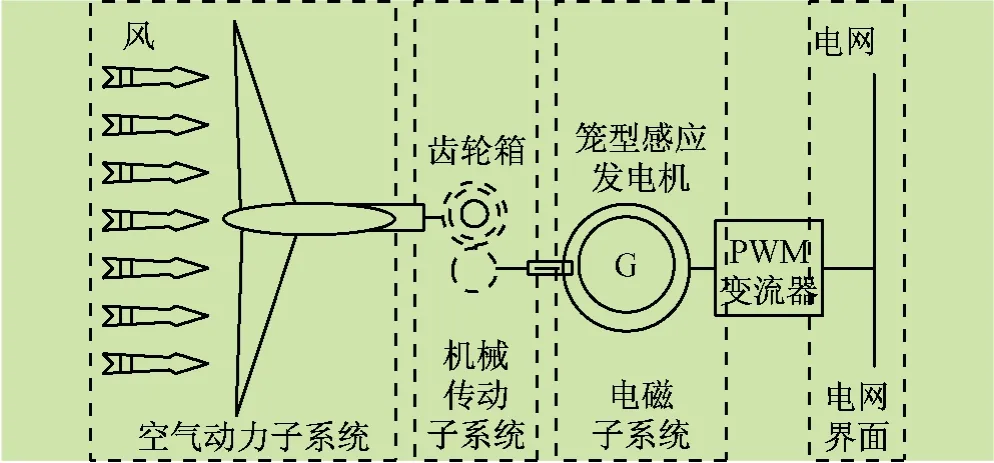
图1 定速变桨距风能转换系统框图

1.2 机械传动链子系统模型

风力发电系统的刚性传动系统连接风轮和发电机，负责机械能的传递，其主要机械部件为增速齿轮［9］。对于刚性传动链，忽略黏性摩擦，其模型包含一个高速轴或低速轴提供的一阶运动方程，表示为:

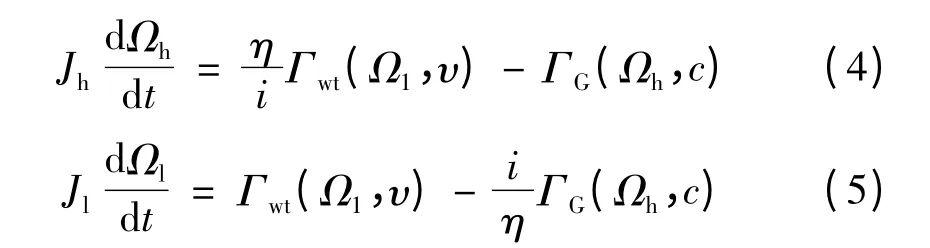
式中:i 为传动比;η 为效率;Γwt(Ω1，υ)是空气动力转矩，以风速υ 作为参数;ΓG(Ωh，c)是电磁转矩，以表示的负荷变量作为参数;Jh、Jl分别是高速轴和低速轴的惯量，其计算表达式为:J1、J2是增速齿轮的惯量，Jwt是风轮的惯量，Jg是发电机的惯量。

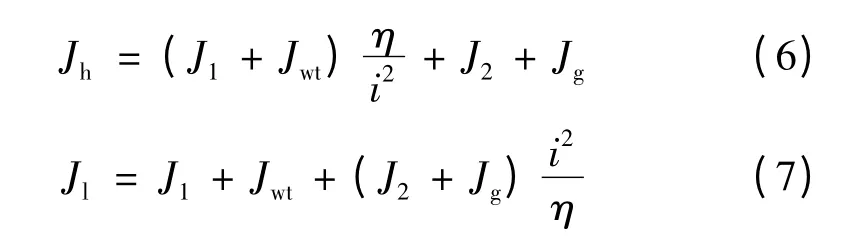
在柔性传动链系统中，高速轴两部分以不同旋转速度旋转，其模型可描述为:

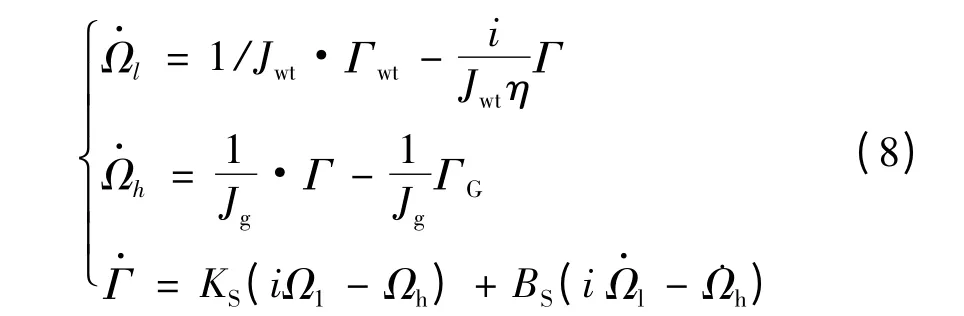
1.3 鼠笼式感应电机模型

设状态向量和输入向量为［10］:

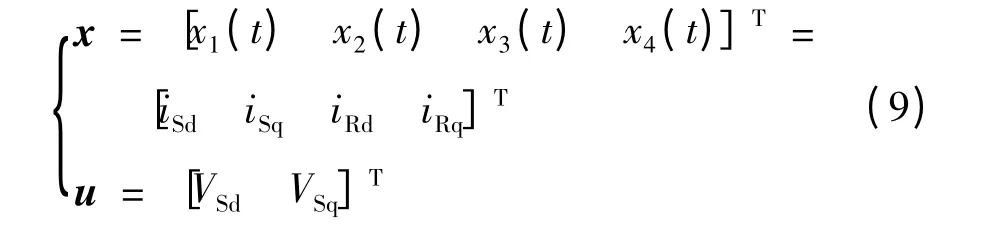
则鼠笼式感应电机的数学模型可描述为:

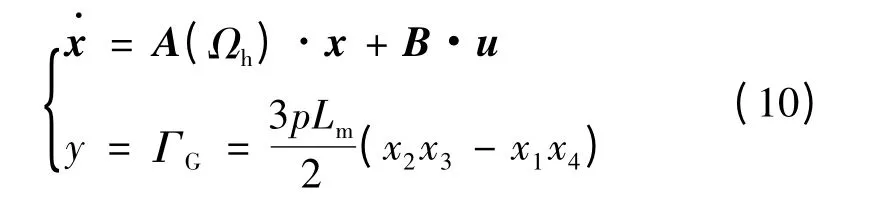
令:σ=1－L2m/LSLR，则矩阵A(Ωh)为:

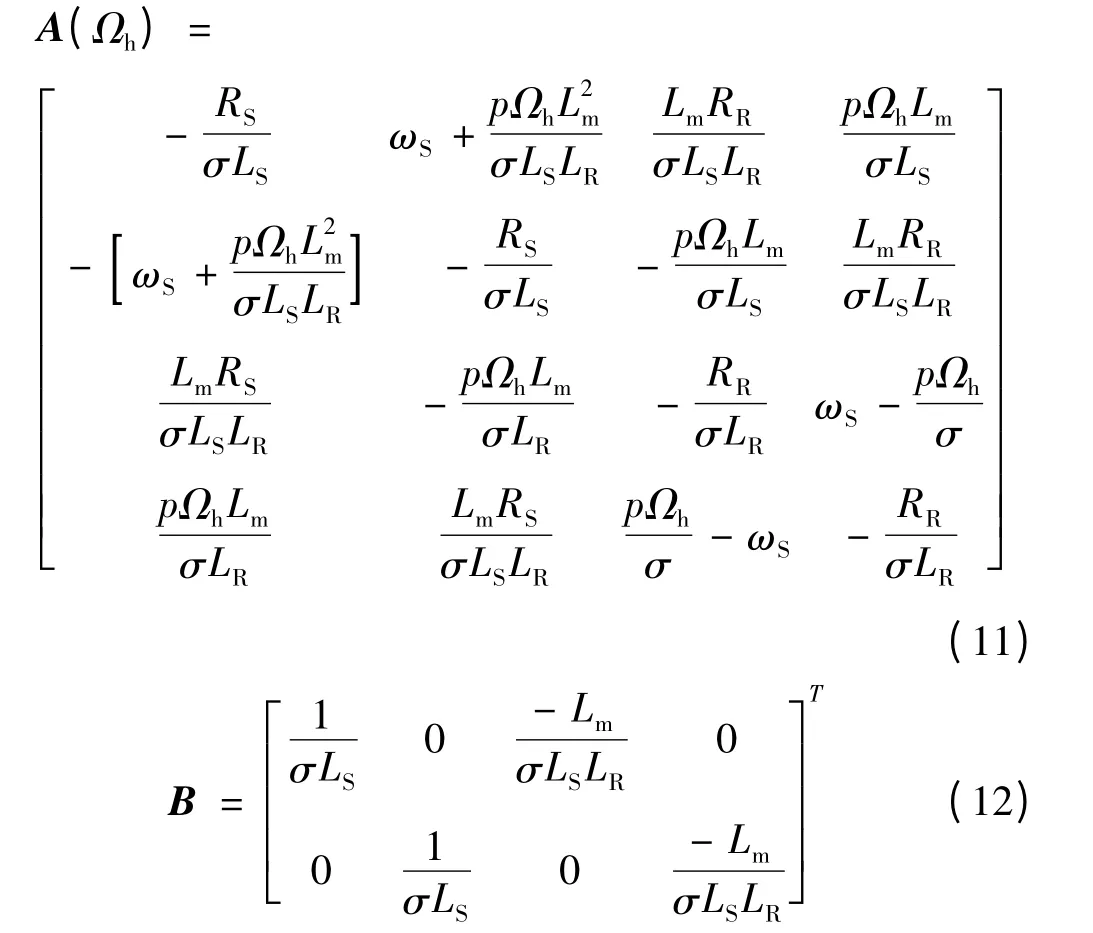
式中:p 是电机的极对数;Lm是定、转子互感;iSd、iSq、iRd、iRq分别是定、转子在d-q 轴坐标下的电流分量;VSd、VSq分别是定子在d-q 轴坐标下电压分量，Ωh为发电机的旋转角速度;ωS是定子的场频，RS、RR分别是定子电阻和转子电阻;LS、LR分别是定子电感和转子电感。忽略静态和粘性摩擦，发电机高速运动轴的方程可描述为:

式中:J 是高速轴的转动惯量;Ωh是高速轴的旋转角速度;Γmec是机械转矩;ΓG是电磁转矩。

2 鼠笼式感应电机风力发电优化跟踪控制器设计

2.1 鼠笼式感应电机优化控制结构

经典PI 控制器的比例系数和积分系数易于设计，控制器设计方便，所取的反馈信息量少，在笼型感应发电机控制中广泛使用［11］。鼠笼式感应电机矢量控制结构由两个解耦环组成，一个是保证感应电机磁场导向的转子磁通环，用以控制转子磁通，另一个是转矩控制环用以控制定子电流。通过对风速、转速测量，可以建立叶尖速度比控制环，对转矩变化的反应较灵敏，通过对电流的控制实现转矩控制环，有助于增加系统的机械灵活性，通过建立功率控制环，使系统运行于最大功率点。

2.2 系统控制环设计

转矩环基于鼠笼式感应电机矢量控制结构直接得出，目标参考转矩可设为［12-14］:

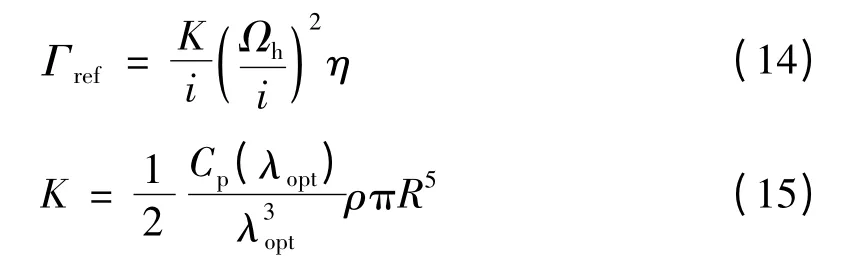
式中:λopt为叶尖速比最优值;η 表示功率传动的总机械效率。

速度环PI 控制器设计为:

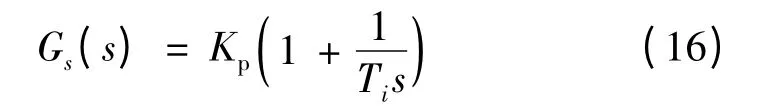
控制器参数为:

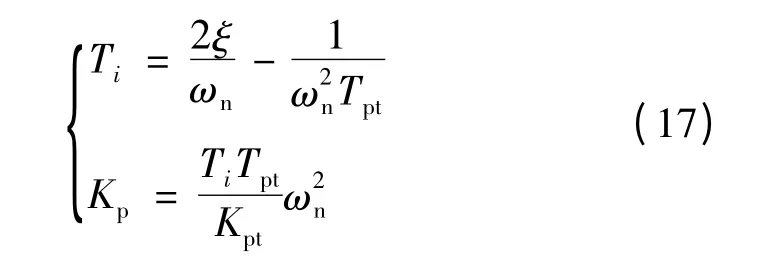
式中:ωn、ξ 为二阶系统的自然频率和阻尼系数;Tpt、Kpt为功率传动模型的时间常数和增益。

功率环也采用PI 控制器设计，实现对有功功率的跟踪控制，保证系统运行到功率最大点［15］。

3 风力发电系统优化跟踪控制仿真

根据系统所构建的鼠笼式感应电机风能转换系统，以2 MW 大功率变速定桨距系统为研究对象，具体参数选取如表1 所示。

表1 系统仿真中用到的参数

在Matlab 环境下进行系统仿真，转速优化跟踪曲线如图2 所示，可见系统能有效实现对参考输入速度的跟踪，图3 给出了转速跟踪的误差曲线，可见系统经过约50 s 左右，便可有效实现转速跟踪，控制器反应迅速，系统响应灵敏，稳态误差小。图4 给出了功率系数和叶尖速比变化曲线，仿真中同时给出了图5、图6所示的输出转矩变化曲线和电磁转矩变化曲线。

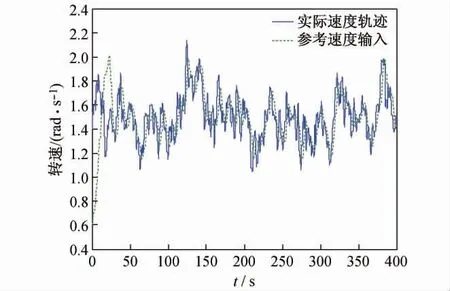
图2 转速优化跟踪曲线

图3 转速跟踪误差曲线

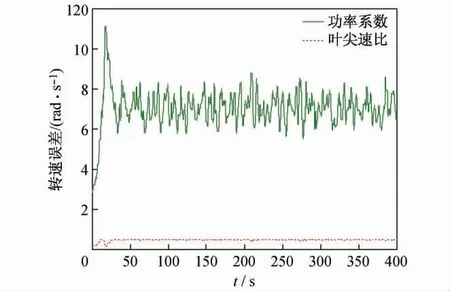
图4 电磁转矩曲线

4 结 语

论文构建了以鼠笼式感应电机为发电系统的大功率定速变桨距风力发电系统，对系统中的空气动力学子系统、机械传动链子系统、电磁子系统进行了详细分析，并给出了对应的数学模型;在Matlab/Simulink 环境下进行了系统仿真，采用模块化设计思想构建了各个子系统，并完成了子系统集成，实现了大功率风能转换系统的建模和鼠笼式感应发电机的矢量控制。详细设计了转矩控制环、速度控制环和功率控制环，通过仿真表明，该系统能实现大功率风能转换系统的最优控制特性跟踪，该系统可以为解决已装机笼型风力发电系统的优化控制提供理论基础，以期通过自动控制技术改造传统产业，以自动化带动工业化，并将理论成果应用于实际风电工程建设及改造。

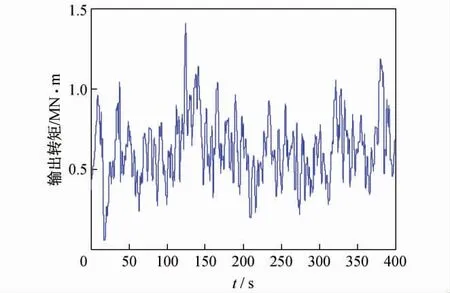
图5 输出转矩曲线

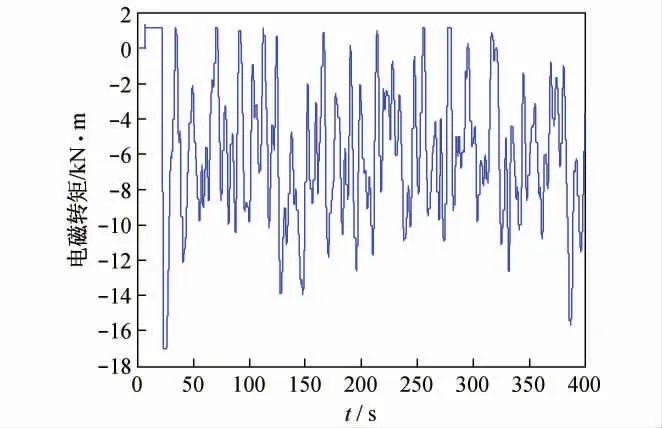
图6 电磁转矩曲线

［1］ BIANCHI F D，DE BATTISTE H，MANTZ R J. Wind Turbine control systems［M］. London:Springer，2007，60-160.

［2］ 杨晓红，葛海涛.基于模糊控制的风力发电机组低风速时最大风能追踪控制仿真研究［J］.机械设计与制造，2010(8):207-209.

［3］ 凌 禹，张同庄，邱雪峰.直驱式风力发电系统最大风能追踪策略研究［J］.电力电子技术，2007(7):3-5.

［4］ 沈艳霞，朱 芸，纪志成.LPV 动态补偿的风能转换系统变桨距控制［J］.控制理论与应用，2009(11):1282-1288.

［5］ 耿 华，周伟孙，杨 耕.变桨距风电系统功率控制的逆系统鲁棒方法［J］.清华大学学报(自然科学版)，2010(5):718-723.

［6］ 高 勇，张文娟，杨 媛，等.基于无源性的变速恒频双馈风力发电机控制系统［J］.电工技术学报，2010(7):130-136.

［7］ 孟 涛，纪志成.风能转换系统双频环滑模控制［J］.电机与控制学报，2009(11):152-156.

［8］ 郑雪梅，李 琳，徐殿国.双馈风力发电系统最大风能追踪滑模变结构控制［J］.控制理论与应用，2010(7):923-926.

［9］ 赵 宇，郭清滔，王 奔，等.基于变结构控制的交流励磁变速恒频风力发电机励磁控制研究［J］. 电力系统保护与控制，2010(7):12-23.

［10］ Parma G，Menezes B R，Braga A P，Costa M A. Sliding mode neural network control of an inducton motor drive. International Jouranal of Adaptive Control and Signal Processing，2003，17(6):501-508.

［11］ MUNTEANU I，BRARCU A I，CUTULULIS N A，et al. Optimal control of wind energy systems［M］. London:Springer，2008，40-80

［12］ NICHITA C，LUCA D，DAKYO B，et al. Large band simulation of the wind speed for real time wind turbine simulators［J］. IEEE Transactions on Energy Conversion，2002(4):523-529

［13］ 惠 晶，杨元侃，顾 鑫.变速恒频无刷双馈风力发电机的功率控制系统［J］.电机与控制应用［J］，2008(7):27-30.

［14］ 潘庭龙，纪志成.基于PSCAD 的变速恒频双馈风电系统建模与仿真［J］.控制理论与应用，2009(6):771-774.

［15］ 朱卫平，王秀丽，王锡凡.分频风力发电系统最优功率输出控制［J］.电力自动化设备，2010，(6):6-10.