临近空间双基地雷达探测性能分析

2013-07-19陈长兴牛德智卞东亮

实验室研究与探索 2013年4期

王博，陈长兴，牛德智，卞东亮

(空军工程大学理学院电子系，陕西西安710051)

0 引言

临近空间是一片有待开发的空间资源，属于空天的结合部，通常被称为“亚太空”、“超高空”。因临近空间作战平台相对于一般飞机和卫星具有飞行高度适中、生存概率高、威胁作用大、部署速度快等独特的优点［1］，而得到各国的广泛关注，美国在临近空间的发展上处于世界领先地位，美国国防技术开发局的ISIS计划目前正处于关键技术攻关阶段。按照计划，该飞艇可留空1 年以上，利用其有源相控阵雷达对空中和地面目标进行监视和跟踪。我国对临近空间有一定的研究。2005 年，由605 所自行研制了“哨兵3”型飞艇［2］。飞艇长30 m、高15 m，载重150 kg，不足的是，该飞艇没有动力装置，主要靠空气浮力升空，飞行高度仅仅达到1 000 m，与国外先进飞艇差距很大。由于我国没有自己的临近空间飞行器作为平台，因此目前对临近空间的相关技术研究均处于理论探索阶段。

2009 年空军工程大学田新华副教授将临近空间作战领域与收发分置体制相结合，提出了一种基于临近空间作战平台的双基地雷达反隐身技术［3］，临近空间双基地雷达的构想应运而生。作为一种新型体制的雷达，目前对其探索相对较少，在探测隐身目标方面的优势已经得到证实，但在探测范围上的优劣却没有较为具体的论述，本文将从这个问题入手。

1 临近空间双基地雷达布站方式

临近空间双基地雷达布站方式如图1 所示，发射站位于地面T 处，接收站置于临近空间平台R 处，基线长为L，地球半径为R0，临近空间平台高度为H，发射站、接收站与地心的连线夹角为θ1，为增加雷达布站时的可操作性，根据余弦定理，计算地心角θ1和平台高度H 与基线长L 之间的关系:

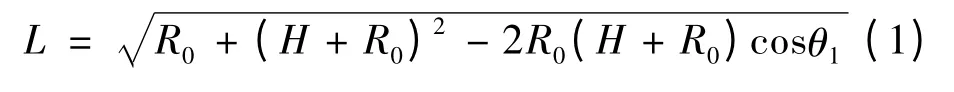
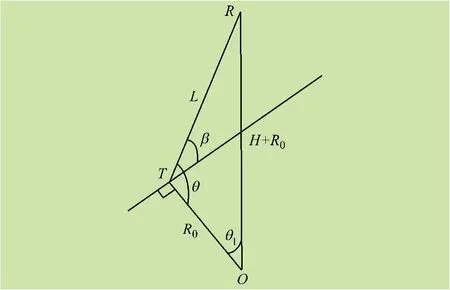
图1 临近空间双基地雷达布站方式

假设平台高度H 固定为20 km，基线长L 随地心角θ1的增大而变大，其关系如图2 所示。这样在将地面发射站固定之后，即可根据基线长度从而选择适当的θ1，进而来确定临近空间平台的位置。

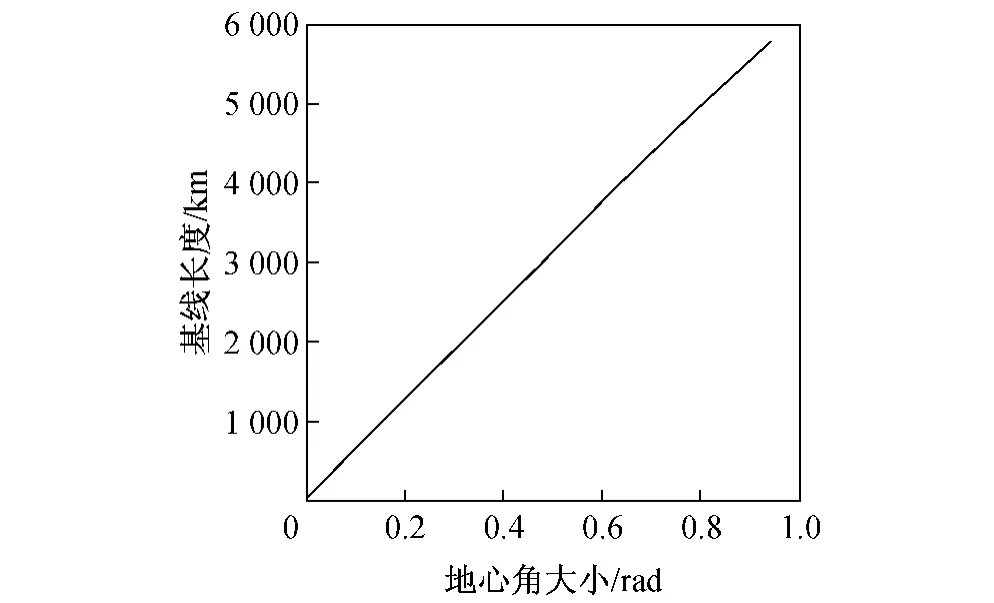
图2 H=20 km 时，L 随θ1 的变化关系

这种布站方式的双基地雷达与地波超视距雷达相比，因将接收站置于临近空间，能克服单一地波雷达探测能力受双程电波绕射传播衰减因素的影响［4］;与天波雷达系统相比，因平台高度的大大降低，可提高对舰船等低速目标的发现概率。对于隐身目标来说，由于大部分隐身目标在上下两侧的隐身能力较弱，所以该类型雷达在探测隐身目标上有突出优势。

2 雷达作用距离

2.1 雷达作用距离

假设不考虑方向图传播因子、大气衰减因子，双基地雷达方程为:

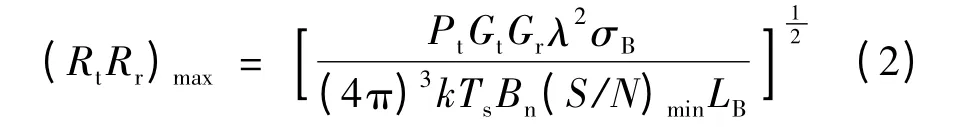
式中:Pt为发射机信号发射功率;Gt、Gr分别为发射天线和接受天线的功率增益;λ 为雷达工作波长;σB为目标的双基地雷达截面积;k 为玻耳兹曼常数;Ts接收机的噪声温度;Bn为接收机检波器前的噪声带宽;(S/N)min为接收机输入端所需的最小信噪比;LB为双基地雷达的总损耗。

记式(2)右端为kB，当双基地雷达系统参数确定后，kB为常数，即目标到T、R 两点的距离乘积(RtRr)max为常数kB。

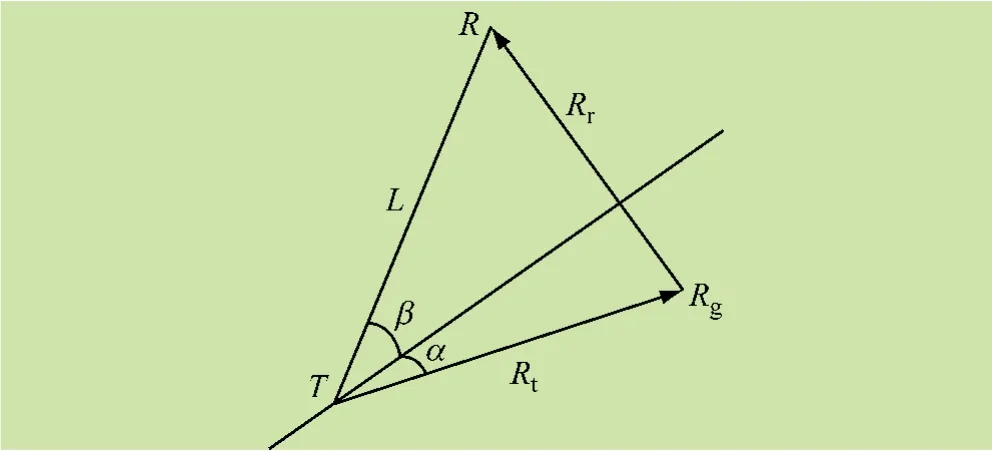
图3 临近空间双基地雷达几何配置

临近空间双基地雷达几何配置如图3 所示，Tg为需要探测的目标;Rt、Rr分别为发射站和接收站到目标Tg的发射距离和接收距离;β 为双基地雷达基线与发射站处地球切线所夹锐角;α 为待探测目标偏离雷达水平线的角度。

根据余弦定理可得:

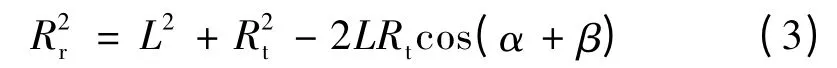
将式(3)代入式(2)，可得:

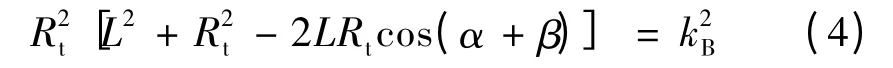
2.2 探测范围分析

当基线长L 确定时，不难确定β 角为定值。因此在式(4)中，探测距离Rt仅与α 角有关。而在L 取不同值时，对于雷达的覆盖面积又有不同的算法［5］:

3 仿真

3.1 临近空间双基地雷达的探测性能仿真

为方便讨论，以下仿真中取地球半径R0=6 371 km。下面对临近空间双基地雷达探测范围进行仿真，仿真参数如下:发射机功率Pt=200 kW，发射天线功率增益Gt=35 dB，接收天线功率增益Gr=35 dB，发射波长λ=0.3 m，双基地雷达的目标RCS 为σB=－10 dB，kTs=4 ×10－21W/Hz，接收机噪声带宽Bn=1 MHz，检测所需最小信噪比(S/N)min=12 dB，双基地雷达的总损耗LB=10 dB。

3.1.1 固定基线条件下的仿真

固定临近空间平台H =20 km，取基线长L =80 km，在图1 中，由各角度关系可计算出∠β =0.246 5，根据(4)式，图4 给出了在雷达基线长度为80 km，雷达平台高20 km 时，探测距离Rt与α 角的关系，随着α 角的增大，探测距离Rt逐渐减小。这是由于双基地雷达的探测范围在平面上类似于一个椭圆，在α 角为零时，探测半径Rt与基线L 的延长线即椭圆的长轴部分重合。当α 角增大时，最大探测半径Rt所对应的点沿着椭圆边缘移动，探测半径逐渐减小。按照上述方法计算，最远探测距离为α=0 时，Rt≈107.036 km。

根据雷达方程，很容易得出在相同参数条件下，单基地雷达的最大探测距离为RMmax≈61.53 km;地基双基地雷达的最大探测距离为R'tmax≈92.31 km。由此可见，临近空间双基地雷达有较大的低空探测距离。

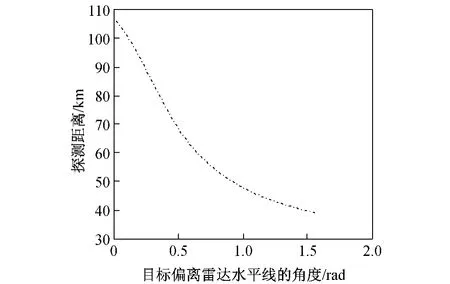
图4 α 角与探测距离Rt 的关系

3.1.2 变基线条件下的仿真

为探究临近空间双基地雷达的最大作用距离，固定临近空间平台H=20 km，取α =0。利用MATLAB，根据式(4)可得出当基线L 变化时，雷达探测距离Rt的变化关系如图5 所示。随L 的增大，Rt增大。

3.1.3 变平台高度条件下的仿真

固定基线L=120 km，取α=0。利用Matlab，根据式(4)可得出当雷达平台高度H 变化时，探测距离Rt的变化关系如图6 所示。随H 的增大，Rt减小。

3.2 影响雷达探测性能因素分析

3.2.1 发射机输出功率的改变对探测性能的影响

根据方程2，不同的发射机输出功率会产生不同的探测距离，而发射机置于地面，其功率大小的调节相对容易。下面通过仿真分析当发射功率分别为Pt=30 kW，Pt=50 kW 和Pt=200 kW，其他参数同3.1，图7 给出了发射机功率变化时双基地雷达探测范围的变化。

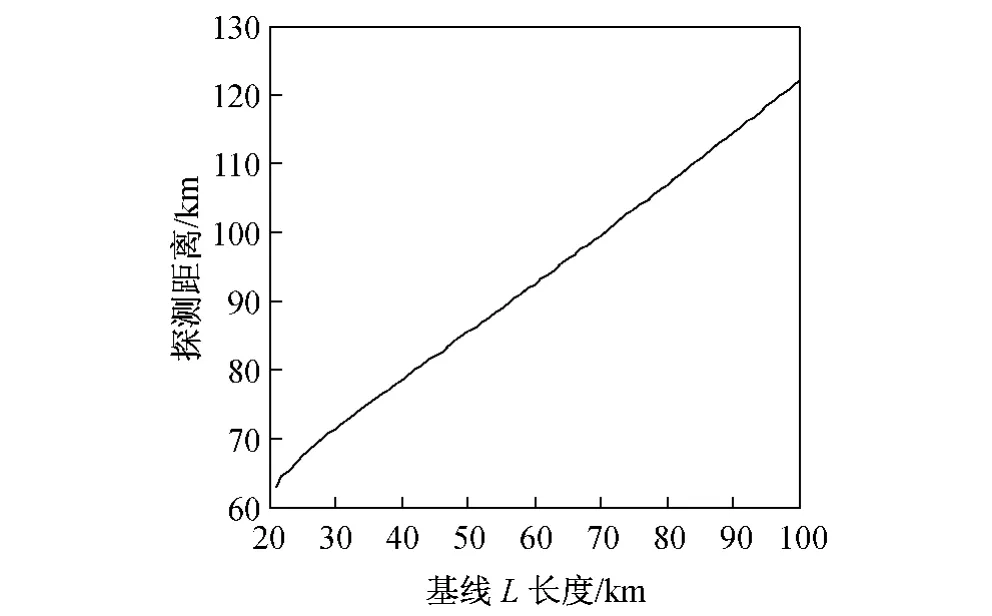
图5 基线L 与探测距离Rt 的关系

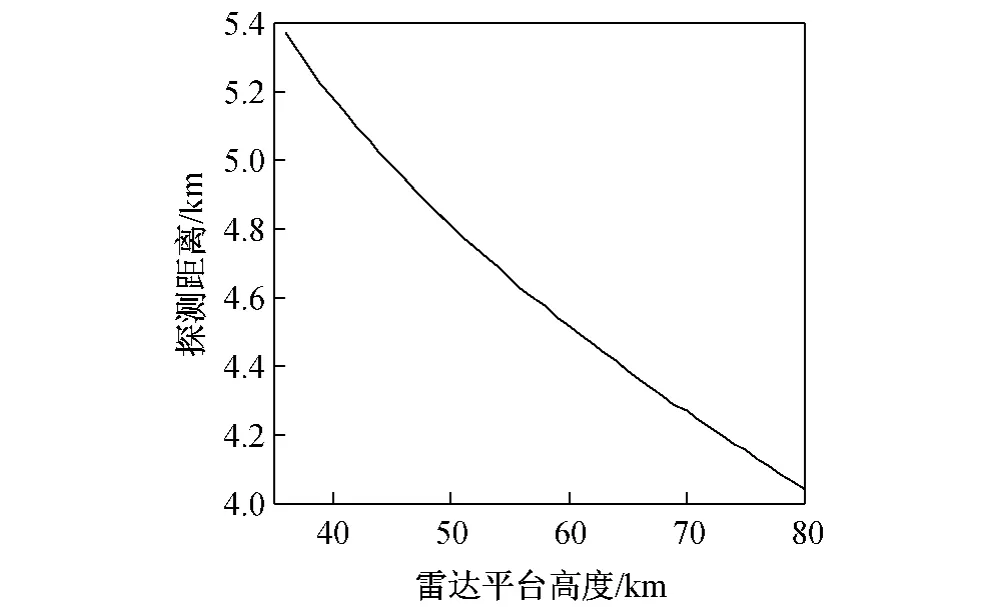
图6 雷达平台高度与探测距离Rt 的关系

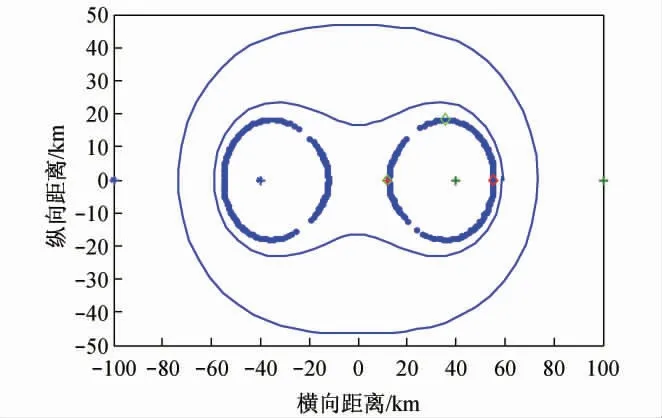
图7 不同发射功率时的双基地雷达探测范围图

图7 中的卵形线由内到外分别为发射功率为30、50 和200 kW 时的探测范围，仿真结果可知:①Pt=30 kW 时为双卵形线，最大可探测距离为95.22 km，最大探测范围为2 061 km2。②Pt=50 kW 时为单卵形线，最大可探测距离为98. 91 km，最大探测范围为4 751.2 km2。③Pt=200 kW 时为单卵形线，最大可探测距离为113.37 km，最大探测范围为11 193.1 km2。

3.2.2 发射波波长的改变对探测性能的影响

为讨论波长的影响，在甚高频(VHF)、特高频(UHF)、超高频(SHF)、极高频(EHF)频段内各取一波长。取λ 分别为0.01、0.05、0.3、1 m，其他参数同3.1。图8 显示的是发射波分别在上述4 种波长下，雷达的探测范围，由内到外分别是波长为0.01、0.05、0.3、1 m 时的探测范围。图9 所示为图8 中左侧双卵形的放大图。

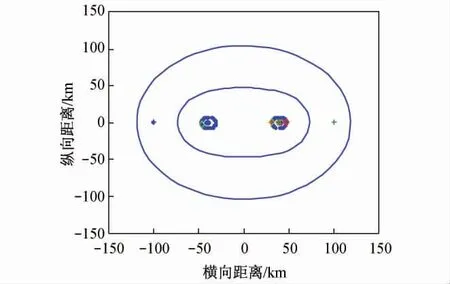
图8 不同波长时的双基地雷达探测范围图

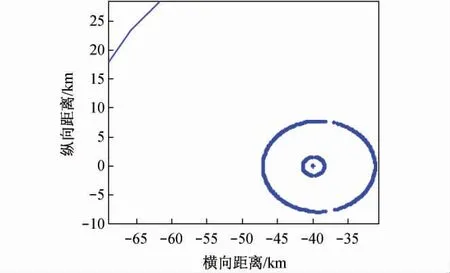
图9 图8 中左侧双卵形的放大图

仿真结果:①λ=0.01 m 时为双卵形线，最大可探测距离为81.53 km，最大探测范围为15.26 km2。②λ=0. 05 m 时为双卵形线，最大可探测距离为87.16 km，最大探测范围为381.60 km2。③λ =0.3 m时与3.2 中①的第二种情况相同。④λ=1 m 时，最大可探测距离为113.36 km，最大探测范围为39 002.1 km2。

在式(2)中影响探测性能的其它因素，如目标RCS、收发天线功率增益积GtGr在文献5 中有详细说明。