对2012年江苏高考第14题的探讨
2013-07-19张冕
张 冕
(无锡市第六高级中学,江苏 无锡 214000)
高中物理有关弹簧的问题一直是个典型又重要的问题,2012年江苏高考再次以计算题的形式考查了此类问题.
原题.某缓冲装置的理想模型如图1所示,劲度系数足够大的轻质弹簧与轻杆相连,轻杆可在固定的槽内移动,与槽间的滑动摩擦力恒为f.轻杆向右移动不超过l时,装置可安全工作.一质量为m的小车若以速度v0撞击弹簧,将导致轻杆向右移动轻杆与槽间的最大静摩擦力等于滑动摩擦力,且不计小车与地面的摩擦.
(1)若弹簧的劲度系数为k,求轻杆开始移动时,弹簧的压缩量x;
(2)求为使装置安全工作,允许该小车撞击的最大速度vm;
(3)讨论在装置安全工作时,该小车弹回速度v′和撞击速度v0的关系.
标准答案:
(1)轻杆开始移动时,弹簧的弹力F=kx,且F=f,解得

图1
(2)设轻杆移动前小车对弹簧所做的功为W,则小车从撞击到停止的过程中,运用动能定理,可得

同理,小车以vm撞击弹簧时有-f·l-W=
本文的讨论重点在第(2)问,不涉及第(3)问,所以该问的答案就不给出了.
第(2)问的突破口在于对“轻杆”运动方式的理解.轻杆不计质量,所以就没有惯性,因此当弹簧弹力大于轻杆所受最大静摩擦力时,它能立刻获得与小车相同的速度,并时刻保持与小车同速;当弹力小于最大静摩擦力时它又能瞬间静止.为了不与下文涉及的模型冲突,这里称这种“瞬动瞬停”的轻杆为“理想轻杆”.我们用Mathematica模拟了这一运动,图2、图3分别表示小车的v-t图像、水平轻杆的v-t图像.从两个物体的v-t图像可以看出,小车一直减速,在弹簧形变量x超过f/k后弹力大于轻杆受到的最大静摩擦力,轻杆瞬间获得速度并在随后的时间里与小车同步减速.从它们相对速度随时间的变化图(图4)可以更明显地看出,在轻杆开始运动直至减速到速度为0的过程中,它们保持相对静止,而弹簧的形变量也将保持x=f/k不变,其蕴含的弹性势能也不变,所以答案中的W 只需考虑轻杆移动前小车对弹簧做的功就可以了,并且此W 与小车的初速度无关.

图2
图3
图4
上面的讨论是基于“理想轻杆”、“瞬动瞬停”的特点,但是实际情况下的物体并不具有这样的特点,而应该依据牛顿定律运动,学生也更习惯处理按牛顿定律运动的物体.那么如果考虑杆的质量但仍旧保证其很轻(远小于小车质量),在符合牛顿定律描述的运动下,是否也能很好的逼近此题中设置的理想情形呢?答案所给的解题方法是否适用于牛顿定律描述下的轻杆运动情形,还是只能处理“理想轻杆的问题”?为了更好的探究这一问题,我们利用Mathematica做了进一步的模拟.在模拟中设置了如下的参数:小车的质量M车=1000kg,轻杆的质量M杆=1kg,轻杆所受最大静摩擦力f=10N,弹簧劲度系数k=2N/m.
首先假设小车以4m/s的初速度撞击弹簧,在小车减速到0的过程中,有了质量的轻杆按照牛顿定律加速和减速,图5,图6分别表示小车和轻杆的v-t图像,从图中看出轻杆和小车不再能保持相对静止,弹簧形变化量随时间变化图像如图7所示,从图7可以看出弹簧的形变量出现了周期性的变化,所以在计算小车对弹簧所做功时就无法只研究轻杆开始运动之前的阶段了,这似乎让人对答案在此情形下的适用性产生了疑问.但是由于摩擦力不断做负功消耗系统的能量,弹簧的振幅越来越小,当小车减速到0时,形变量有趋于一个定值的趋势(图7).进一步研究发现,现,在以不同初速度撞击下,每当小车减速到0时,弹簧形变量的最终值都为5m,见表1.(之所以有一些波动,是由于这里计算时轻杆的相对质量不够小,如果我们把小车的质量设定为10 000kg,得到的数据见表2.可以看到波动更小了,因此有理由相信极限情况下,弹簧最终形变量为一定值).也就是说,虽然整个过程中弹簧的形变量在不断变化,但是小车减速到零时,弹簧最终储存的弹性势能是一定的.从模拟时所设定的参数可以看出,弹簧最终的形变量等于f/k,对应的弹性势能与原题答案中所用的W一致.

图5

图6
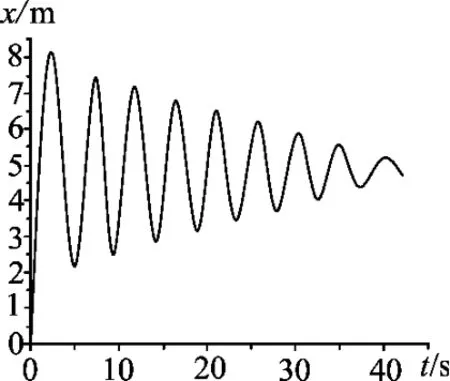
图7

表1 M车=1 000kg;M杆=1kg,小车以不同初速度减速到0时的弹簧最终形变量

表2 M车=10 000kg;M杆=1kg,小车以不同初速度减速到0时的弹簧最终形变量
由此看来,我们可以以小车开始接触弹簧到速度减为0整个阶段为研究过程,仍然采用与原题答案相同的解题方法得到相同的结论.按照牛顿定律运动的轻杆和“理想轻杆”的运动在极限情况下是一致的.2012年的这道高考计算题虽然是一个涉及弹簧的老情景,但是由于出现了不计质量的“轻杆”,使得整个分析过程和最终的状态都出现了新的变化,这是值得我们好好分析的.
