索赔额服从混合指数分布的破产概率及其渐近估计

2013-07-16许璐赵闻达余茜茜

五邑大学学报（自然科学版） 2013年1期

关键词：指数分布概率论学报

许璐，赵闻达，余茜茜

许璐1，赵闻达2，余茜茜1

（1.江汉大学数学与计算机科学学院，湖北武汉 430056；2.明尼苏达大学双城分校数学系，美国明尼苏达州 55414）

运用古典概率论的有关知识，针对个体索赔额服从混合指数分布的破产概率问题，通过建立合适的数学模型导出了它的最终破产概率的显式表达式，并得到了它的渐近估计. 所得结果包含了现有文献的相关结论.

混合指数分布；最终破产概率；渐近估计；显式解

文献[1-2]利用计算机技术对一些具体分布的破产概率进行了数值计算分析；文献[3]对任意的初始盈余与任意的个体索赔额给出了破产概率的递推解、隐式解，同时得到了指数分布破产概率的显式解；文献[4-5]给出了最终破产概率与有限时间的生存概率的显式解，却没有讨论刻画保险公司破产概率的渐近估计；文献[6-10]讨论了几种不同分布模型的破产概率问题，但是，没有涉及到个体索赔额服从混合指数分布的破产概率问题. 本文主要是在古典概率理论的基础上讨论个体索赔额服从混合指数分布的破产概率，并得到了它的渐近估计.

1 模型的描述

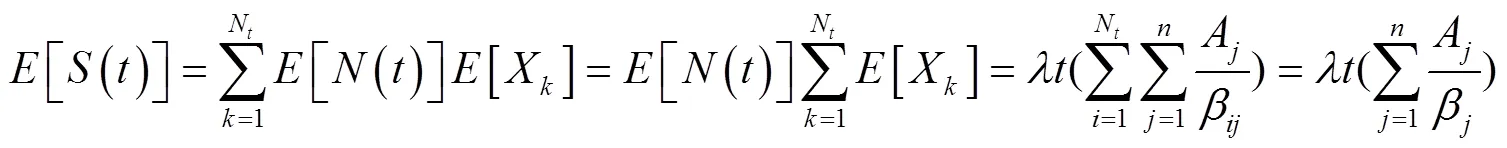
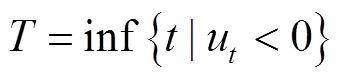
2 主要结果

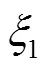
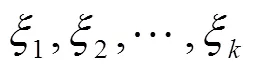
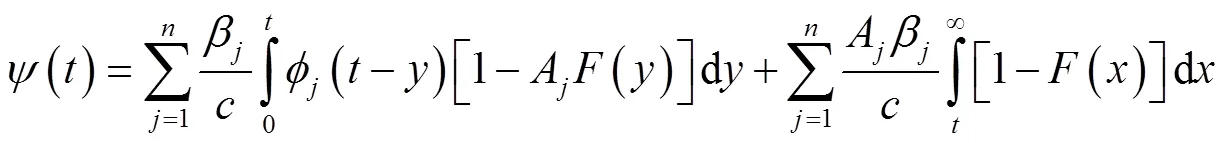
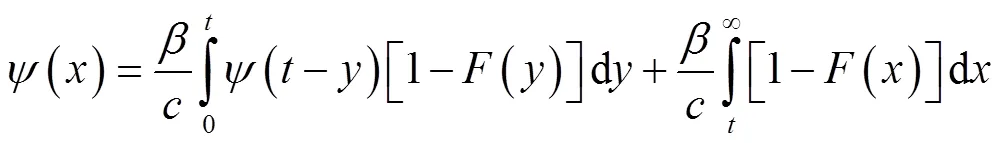
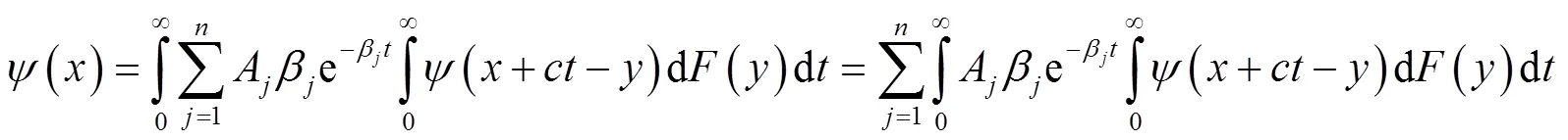
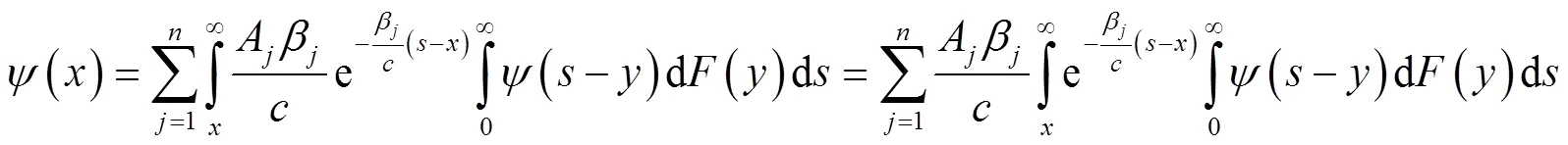
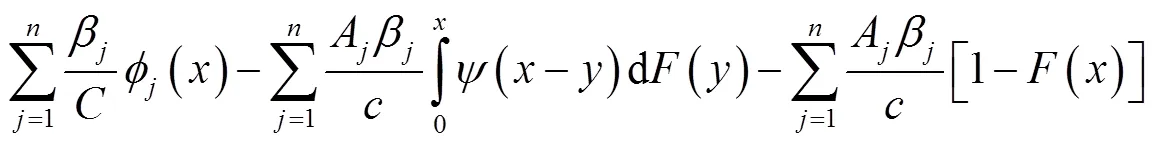
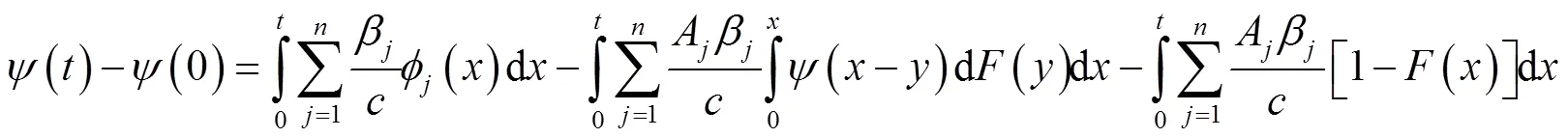
所以

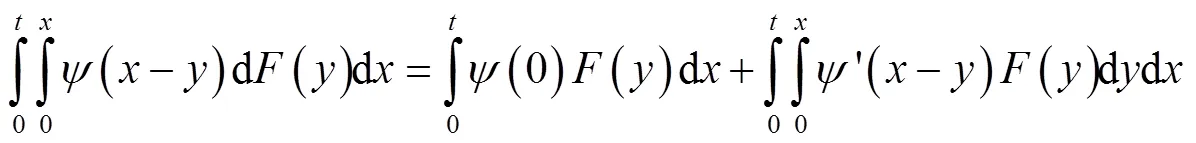
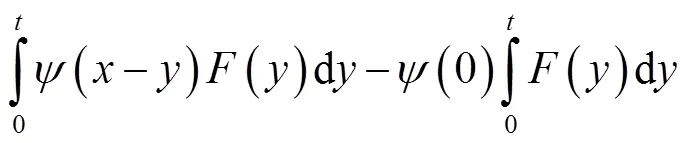
将式（4）代入式（3）得：

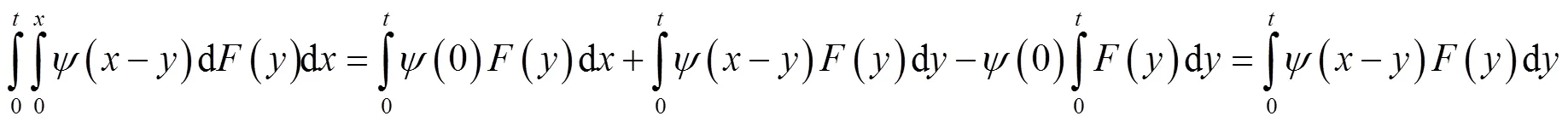
故

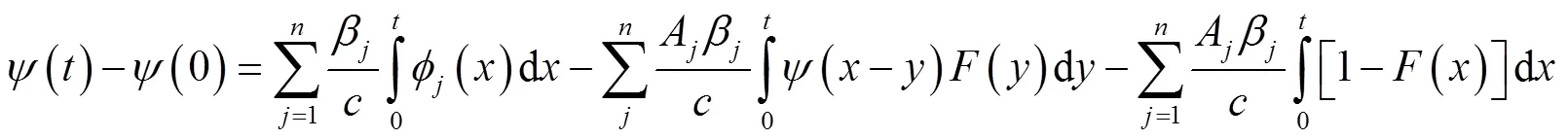
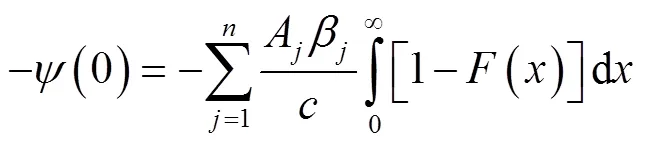
所以

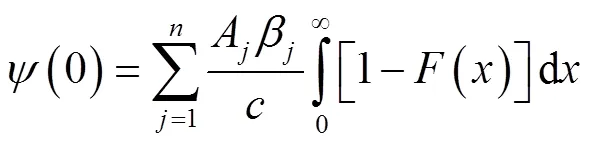
从而可知：

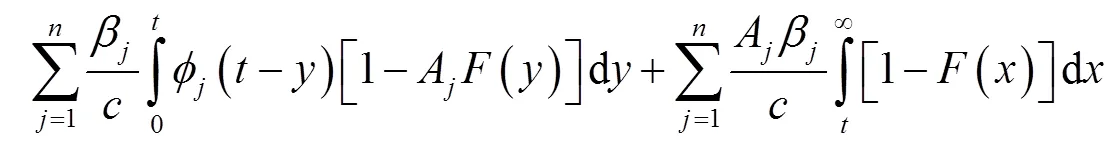
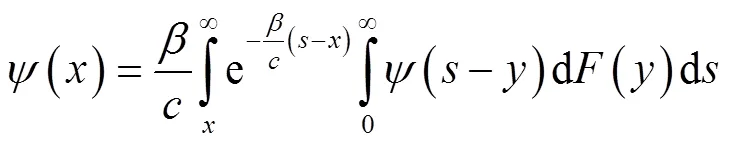
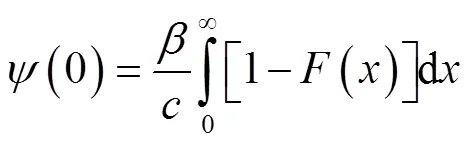
故

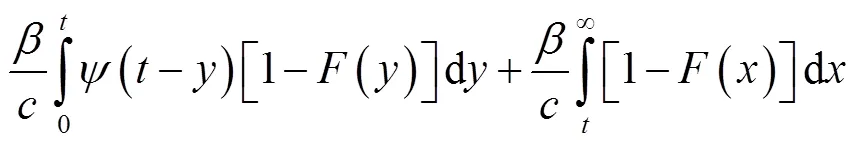
从而式（2）得证，并且这与文献[3]中的结果一致.

定理2 设个体索赔额服从混合指数分布，则索赔总额也服从混合指数分布的最终破产概率的渐近估计为：

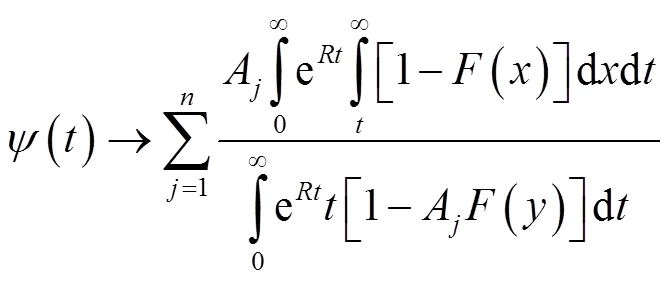
证明采用通常的卷积记法，利用更新方程的定义有

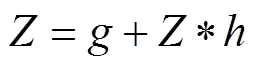
由式（1）知：

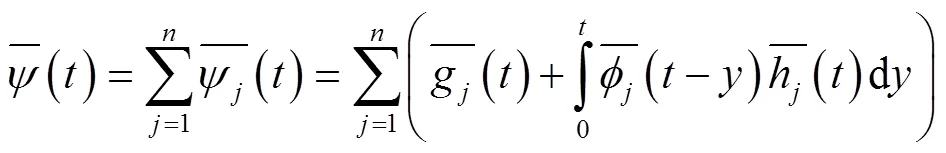
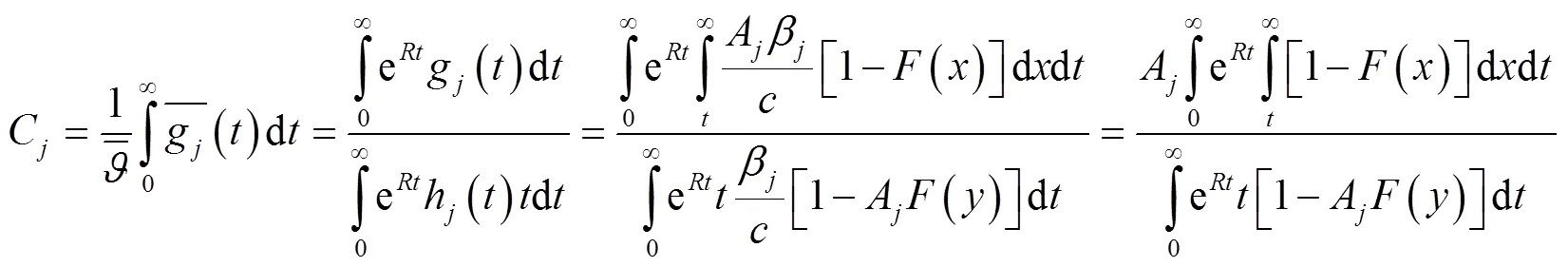
[1] SEAL H L. Numerical calculation of probability of ruin in the Poisson/exponential case [J]. Mitteilangen der Vereinigung Schmeicerischer Versichrungs Mathematiker, 1972, 72: 77-100 .

[2] RAMSAY C M. On an integral equation for discounted compound-Annuity distributions [J]. ASTIN Bulletin, 1989, 19(2): 191-198.

[3] GERBER H U. 数学风险论导引[M]. 成世学，严颖，译. 北京：世界图书出版公司，1997.

[4] 成世学，伍彪. 完全离散的经典风险模型[J]. 运筹学学报，1998, 2(3): 42-54.

[5] SHIU E S W. The probability of eventual ruin in the compound binomial model [J]. ASTIN Bulletin, 1989, 19(2): 179-190.

[6] 许璐. 离散经典风险模型中的破产概率及其渐近解[J]. 江汉大学学报：自然科学版，2001, 18(3): 43-45, 78.

[7] 许璐. 索赔总额服从几何分布的破产概率及渐近解[J]. 高等数学通报，2001(l): 28-30.

[8] 成世学，朱仁栋. 完全离散的经典风险模型中的渐近解和Lundberg型不等式[J]. 数学学报，2001, 16(3): 348-358.

[9] 成世学. 破产论研究综述[J]. 数学进展，2002, 31(5): 403-422.

[11] 梁之舜，邓集贤，杨维权，等. 概率论与数理统计[M]. 北京：高等教育出版社，1990.

[责任编辑：熊玉涛]

Ruin Probability and Asymptotic Estimate When Claims Obey a Mixed Exponential Distribution Model

XULu1, ZHAOWen-da2, YUQian-qian1

(1. School of Mathematics and Computer Science, Jianghan University, Wuhan 430056, China; 2. Department of Mathematics, University of Minnesota Twin Cities, Minnesota 55414, U.S.A.)

The classical probability theory is used to derive solution of the ultimate ruin probability in a mixed exponential distribution model, and its asymptotic estimation is obtained. The related results in literatures are improved in this conclusion.

mixed exponential distribution; the ultimate ruin probability; asymptotic estimation; explicit expression

1006-7302（2013）01-0006-05

O211.67

2012-10-26

国家自然科学基金资助项目（No.10961003）；江西省教育厅科学计划资助项目（GJJ08338）

许璐（1969—），男，湖北武汉人，副教授，硕士，研究方向为概率论与数理统计.