Parallelizing Modif i ed Cuckoo Search on MapReduce Architecture
2013-07-14ChiaYuLinYuanMingPaiKunHungTsaiCharlesWenandLiChunWang
Chia-Yu Lin, Yuan-Ming Pai, Kun-Hung Tsai, Charles H.-P. Wen, and Li-Chun Wang
1. Introduction
Meta-heuristics such as particle swarm optimization(PSO) and cuckoo search (CS) are widely used in engineering optimization. PSO was inspired by foraging social behavior of birds and fi shes[1]. At the beginning, the species have no idea about the food location and thus search according to their experience and intuition. Once an individual fi nds the food, it informs other individuals of such location. Accordingly, others adjust their flight.Bird/f i sh foraging behavior is a concept of socially mutual inf l uence, which guides all individuals to move toward the optimum. PSO is prevailing because it is simple, requires little tuning, and is found effective for problems of wide-range solutions.
Moreover, cuckoo search (CS), an optimization algorithm was proposed in 2009[2]. The cuckoo eggs mimic the eggs of other host birds to stay in their nests. This phenomenon leads to the evolution of egg appearance towards optimal disguise. In order to improve the performance of cuckoo search, a modif i ed cuckoo search(MCS) was later proposed in 2011[3]and successfully demonstrated good performance. Based on [3], we parallelize MCS to propose a MapReduce modif i ed cuckoo search (MRMCS) in this work. As a result, our MRMCS outperforms previously proposed MapReduce particle swarm optimization (MRPSO)[4]on all evaluation functions and two engineering design problems in terms of both convergence of optimality and runtime.
MapReduce[5]is a widely-used parallel programming model in cloud platforms and consists of mapping and reducing functions inspired by dividing and conquering.Mapping and reducing functions execute the computation in parallel, combine the intermediate result, and output the fi nal result. Independent data are suitable for the MapReduce computing. For example, in the k-means algorithm, each data node computes the distance from itself to all central nodes and thus the work[6]proposed its parallelized version on MapReduce in 2009. Similarly,particle swarm optimization (PSO) addresses that each data node computes its own best value by itself and thus were also successfully parallelized on a MapReduce framework[4].
Since PSO can be successfully parallelized into MRPSO[4], we are motivated to parallelize MCS on a MapReduce architecture and compare the performance of MRMCS with that of MRPSO. However, two critical issues are worth pointing out when parallelizing MCS on a MapReduce architecture: 1) job partitioning (i.e. which jobs go to the mappers and which jobs go to the reducers) needs to be decided in MRMCS; 2) the support of information exchange is critical during evolution in MCS. However, an original MapReduce architecture like Hadoop cannot support this and thus need proper modif i cation. Therefore,this work is motivated to deal with these two problems to enable good parallelism on MRMCS.
The rest of the paper is organized as follows. Section 2 introduces the fundamentals of MCS, and Section 3 describes the MapReduce architecture in detail. MRMCS is proposed and elaborated in Section 4. Section 5 shows several optimization applications with MRMCS and compares their performance and runtime with MRPSO.Finally, Section 6 concludes the paper.
2. Modified Cuckoo Search
CS was proposed for optimization problems by Yang et al. in 2009[2]. Later, in order to improve the performance of the baseline CS, Walton et al. in 2011 added more perturbations to the generation of population and thus proposed MCS in [3]. In this work, we further parallelize MCS on a MapReduce architecture and propose MRMCS.
The original CS was inspired by the behavior of cuckoo laying eggs. Cuckoos tend to lay eggs in the nests of other host birds. If the host birds can differentiate cuckoo eggs from their own eggs, they may throw away cuckoo eggs or all eggs in the nest. This leads to the evolution of cuckoo eggs mimicking the eggs of local host birds. Yang et al.[2]conducted the three following rules from the behavior of cuckoo laying eggs for optimization:
· Each egg laid by one cuckoo is a set of solution coordinates and is dumped in a random nest at a time.
· A fraction of the nests containing the eggs (solutions)with best fitness will carry over to the next generation.
· The number of nests is fi xed and there is a probability that a host can discover such alien egg. If this happens, the host can either discard the egg or the nest, resulting in building a new nest in a new location.
Besides the three rules stated above, the use of Lévy fl ight[7]for both the local and global search is another important component in CS. The Lévy fl ight, also frequently used in other search algorithms[7], is a random walk in which the step lengths have a probability distribution with heavy tails. The egg generated by Lévy fl ight compares its fitness value with that of the current egg.If the fitness value of the new egg is better than the current one, the new egg takes place of the position. The random size of Lévy fl ight is controlled by a constant step size α where α can be adjusted according to the problem size of target applications. The fraction of nests to be abandoned is the only one parameter which is needed to be adjusted during the CS evolution.
In order to speed up the convergence of evolution,Walton et al.[3]proposed MCS. There are two modif i cations over CS. The fi rst change is that the step size1α is no longer a constant and can decrease as the number of generation increases. Adjusting1α dynamically leads to faster convergence on optimality. At each generation, a new step size of Lévy fl ight is

where A is initialized as 1 and G is the generation number.This setting is used for deciding the fraction of nests to be abandoned.
The second change is the information exchange between eggs. In MCS, eggs with the best fi tness values are put in the top-egg group. Every top egg will be paired with a randomly-picked egg. During the selection process, if the same egg is picked, a new egg is generated with the step size

Otherwise, a new egg is generated from two top eggs using the golden ratio

The fraction of nests to be abandoned and the fraction of nests to generate next top eggs are two adjustable parameters in MCS. Algorithm 1 shows the details of MCS as follows.
Algorithm 1. MCS Algorithm in [3]
1: A←MaxLévyStepSize
2: φ ←GoldenRatio
3: Initialize a population of n host nests xi,(i=1,2,⋅⋅,n)
4: for all xido
5: Calculate fitness Fi=f( xi)
6: end for
7: Generation number G←1
8: while
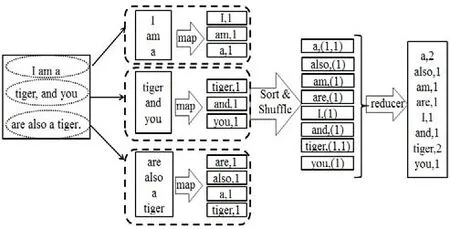
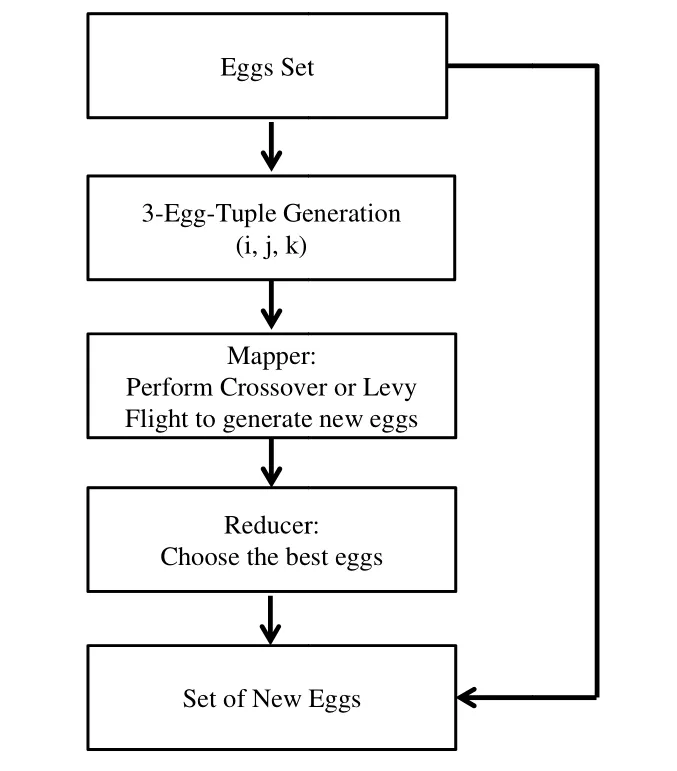
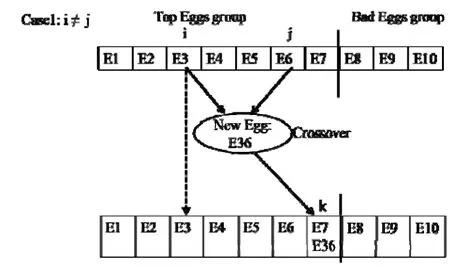
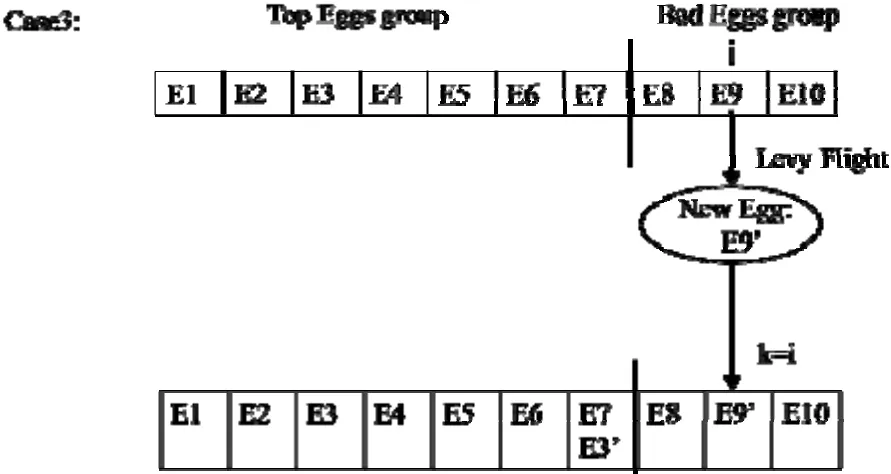
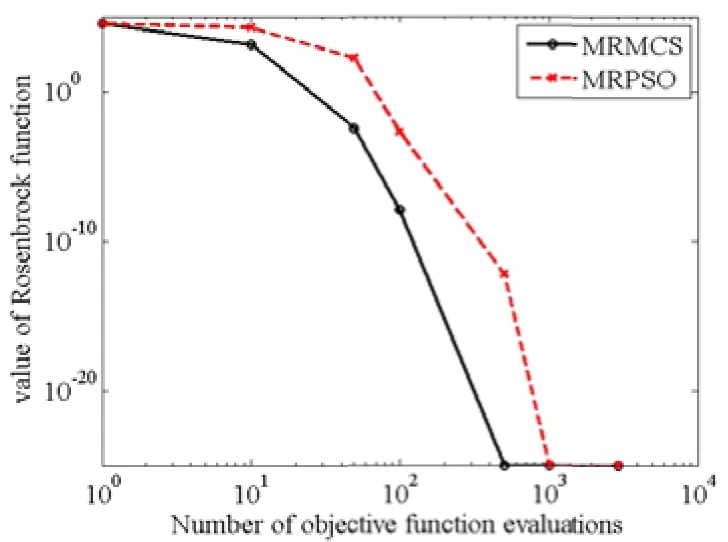
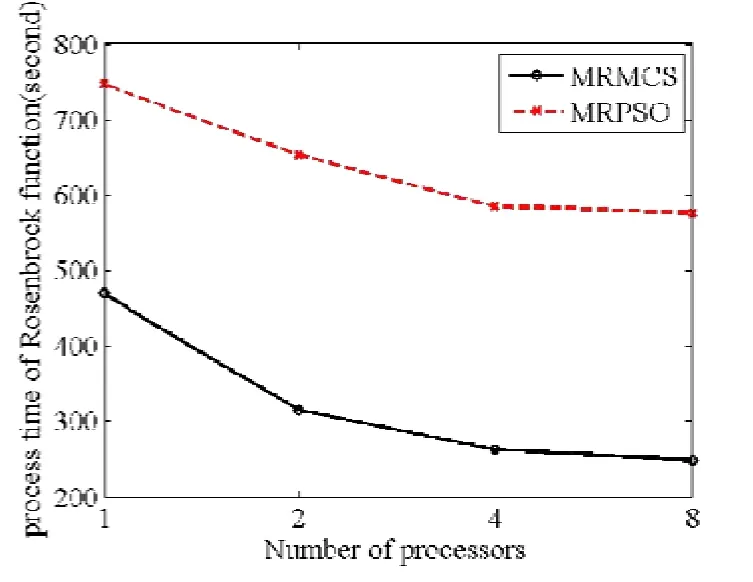
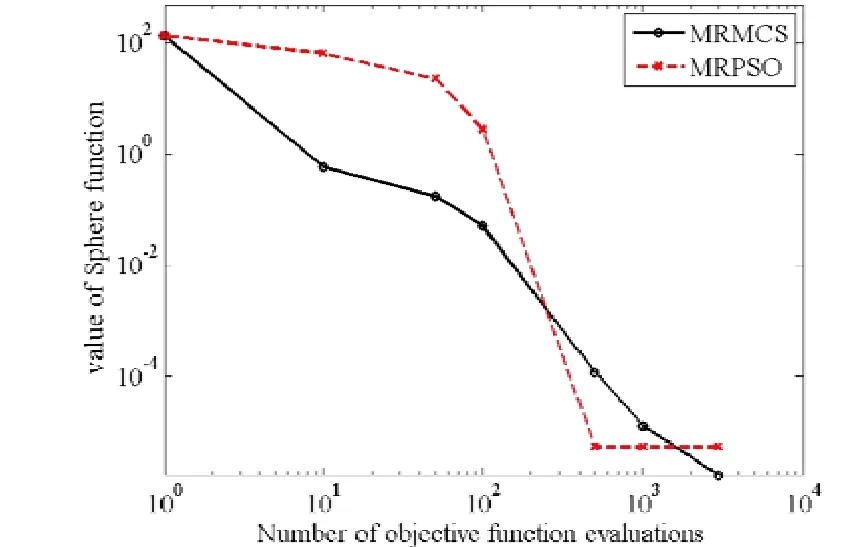
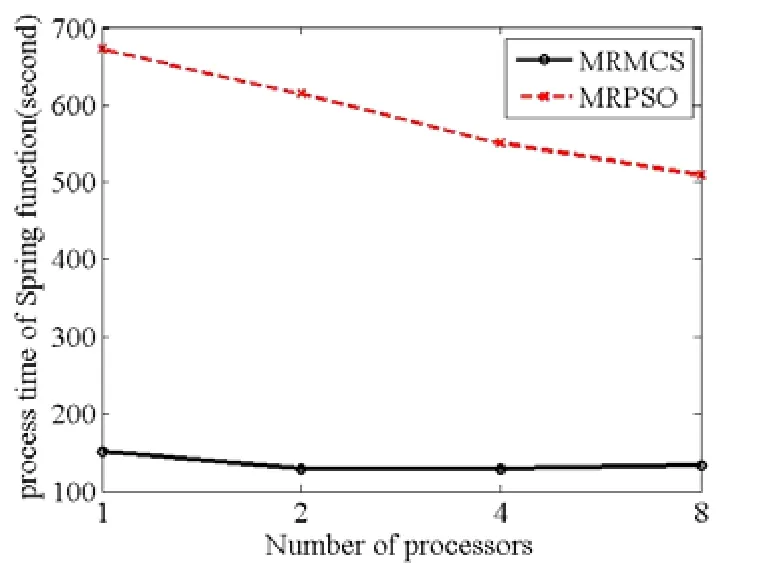
NumberObjectiveEvaluations do 9: G←G+1 10: Sorts nests by order of fitness 11: for all nests to be abandoned do 12: Calculate position xi 13: Calculate Lévy flight step size α1←A 14: Perform Lévy flight from xito generate new egg xk 15: xi← xk 16: Fi←f( xi) 17: end for 18: for all of the top nests do 19: Calculate position xi 20: Pick another nest from the top nests at random xj 21: if xi=xjthen 22: Calculate Lévy flight step size α←A/ G2 2 23: Perform Lévy flight from xito generate new egg xk 24: Fk=f( xk) 25: Choose a random nest l from all nests 26: if Fk>Flthen 27: xl←xk 28: Fl←Fk 29: end if 30: else 32: Move distance dx from the worst nest to the best nest to find xi 33: Fk=f( xk) 34: Choose a random nest l from all nests 35: if Fk>Flthen 36: xl←xk 37: Fl←Fk 38: end if 39: end if 40: end for 41: end while MapReduce[5]is a patented software framework introduced by Google to support distributed computing on large data volumes on clusters of computers. MapReduce can also be considered as a parallel programming model and it aims at processing large datasets. A MapReduce framework consists of mapping and reducing functions which are inspired by dividing and conquering. The map function, which is also known as the mapper, parallelizes the computation on large-scale clusters of machines. The reduce function, which is also called the reducer, collects the intermediate results from the mappers and then outputs the fi nal result. In the MapReduce architecture, all data items are represented as the form of keys paired with associated values. For example, in a program that counts the frequency of occurrences for words, the key is the word itself and the value is its frequency of occurrences.Applications with independent input data or computation are suitable to be parallelized on the MapReduce framework. For example, for PSO, each data node can fi nish computing its own best value without acquiring information from other nodes. Therefore, PSO is a good candidate that can be parallelized on the MapReduce framework to save runtime greatly. Such idea was termed MRPSO and realized in [4]. A MapReduce job usually splits the input data set into many independent chunks which are processed by the map function in a completely parallel manner. The map function takes a set of (key, value) pairs and generates a set of intermediate (key, value) pairs by applying a designated function to all these pairs, that is, Before running the reduce function, the shuff l e and sort functions are applied to the outputs from the map function. Then the new outputs become the input to the reduce function. The reduce function merges all pairs with the same key using a reduction function: The input type and output type of a MapReduce job are illustrated in Fig. 1, respectively. The data which is a (key,value) pair is the input to the mapper. The mapper extracts meaningful information from each record independently.The output of the mapper is sorted and combined according to the key and passed to the reducer where the reducer performs aggregation, summarization, fi ltering, or transformation of data and writes the fi nal result. An example of the overall Map/Reduce framework is shown in Fig. 2. This is a program named “WordCount”used for counting the frequency of occurrences for different words. The input data is partitioned into several fi les and sent to different mappers to count occurrences of one target word. The input key is ignored but arbitrarily set to be the line number for the input value. The output key is the word under interest, and the output value is its counts. The shuff l e and sort functions are performed to combine key values output from the mappers. Finally, the reducer merges the count value of each word and writes out the fi nal result(i.e. the frequency of occurrences). Google has published its MapReduce implementation in [5], but has not yet released the system to the public.Thus, the Apache Lucene project developed Hadoop, a Java-based platform, as an open-source MapReduce implementation. Hadoop[8]was derived from Google’s MapReduce architecture and the Google file system (GFS).Data-intensive and distributed applications can work on Hadoop which can support up to thousands of computing nodes. In this work, we referred to [4] and implemented PSO and MCS into MRPSO and MRMCS, respectively, on the Hadoop platform. (input) Fig. 2. Example of a MapReduce framework. Fi g. 3. Overall fl owchart of MR MCS. Fi g. 4. One of the map function in MRMCS. Parallelizinng MCS ona MapReducce architecturre is ellaborated in thhis section. Twwo major probblems remainto be soolved. First,we have todetermine aa strategy forr job paartitioning. Inn other wordss, we need too decide jobss that mmappers andreducers neeed to take ccare, respectiively.Second, informmation is enabbled to exchaange in MRMMCS,annd computingg nodes need tto communicaate with each oother inn the MapRedduce architecture, which wwas not suppoorted orriginally. TTherefore,we propoose 3-egg-tuple trransformationto facilitateexchange infformation betwween egggs. Fig. 3 shhows the oveerall fl ow oof MRMCS.The 3--egg-tuple traansformationfunction outpputs a new sample coomposed of ooriginal samplles (i, j, k) forr mappers, whhere i deenotes the inndex of currrent egg, j iss the indexof a raandomly-pickeed egg to bepaired with eegg i, and k iis the inndex of the nnest for puttinng the new eggg after evoluution.AAfter the 3-eegg-tuple trannsformationprocess, mapppers peerform gold-rratio crossoveer or Lévy fl iight to generaate a neew egg. Laterr, each reduceer chooses the best eggs aas the deescendant sammple among all candidates oof its own. Deetails off three steps sstated above arre further disccussed as folloows. IIn MCS, eggss are separatedd according too top-egg grouups andbad-egg grooups. The eggg picked fromm one top-eggg grouup and the oother one ranndomly pickedd from anothher top-egg group aree first pairedand then MCCS performs tthe crosssover operatioon over the ppair to generatte a new egg.If twoeggs are ppicked fromthe sametop-egg grouup coinncidently, theLévy fl ight iss used insteadd to generate tthe neww egg. Sincethe egg inforrmation is noot preserved oon diffeerent mapperrs in the MMapReduce arrchitecture, wwe commbines informmation from thhree eggs intoo one and suuch funcction is calledd 3-egg-tupletransformatioon. The outputs of 33-egg-tuple traansformationfunction aresets of (current eggindex, randommly-picked eggg index, targeet-nest index for puttiing the new egg) denoted aas (i, j, k). Eacch 3-egg-tuple (i,j, k)is sent to a mmapper for gennerating a neww egg. OOne key chhallenge ofparallelizingg MCS ona MappReduce platform is job parrtitioning. Wee have to deciide whicch jobs go too mappers andd which jobsgo to reducerrs.Thegeneral rule iis that mapperrs take chargee of independeent jobss and reducerss are responsibble for combinning the resullts.Sincce operationsof crossoverand Lévy fl igght for new eggg geneeration are inddependent ammong all samplles, mappers aare assiggned to peerform thenew-egg geeneration. The 3-eggg-tuples arethe inputto new-egggenerationin mapppers and eachh new-egg geeneration canbe divided innto three cases. ·Case 1: Thhe top egg xiaand top egg xxjare not drawwn fromm the same nest. The egg xiis fi rst dupliccated and placed at thhe nest niforthe next genneration. Thenn the egg xiand eggxjare furtherr used to perfform the crossover operation andgenerate a neew egg to beplaced at thee nest nk. Fig.4 showws an examplee for this casee. ·Case 2: The top egg xiaannd top egg xjare drawn from thesame nest. Thhe egg xiis fif rst duplicated and placedat thenest niforthe next geeneration. The Lévy fl ight operration is perfoormed on theegg xiinstead and a new egg is generated to bbe placed at tthe nest nk. FFig. 5 showsan exammple for Case2. Fig. 5. Case two o f the mapper function in MRMCS. Fig. 6. Case thr ee of the mapper function in MRMCS. Fii g. 7. Example on the reduce ff unction. ·Case 3: TThe Lévy fl ighht operation is performed on the baad egg xidireectly and a neww egg is generated to be placed att nk=ni, as shoown in Fig. 6. Reducers aare responsiblle for combingg the intermeediate reesults from mmappers. In MMRMCS, reduccers determine the neext-generationn egg of the nnests, respectivvely. Fig. 7 shhows ann example ffor the reduccer operationn. After mapppers geenerate new eeggs, every nest may contaain more than one eggg. Each reduucer fi nds thebest value froom all eggs in one neest and usesthe egg witth the best vvalue as thenext geeneration. The results of reeducers are ussed as the input to thhe next MRMCCS generationn. Algorithmss 2 and 3 summmarize thedetails of mapper opperations inccluding threecases statedd above and the reeducer operatiions in MRMCCS.A lg orithm 2. MMRMCS on MMap 1: A←MaxLévyStepSize 2 2: φ ←GoldennRatio 33: f( xi) ← TThe fitness ofxi 4: definition:Mapper ( keyy, value ) 5: input: (Lasst iteration Fittness value, S)), S:{(x1, xj,xxk),…,( xn, xj,,xk)}, a set of (the current egg,a random egg, the nest foor putting new egg). 6 6: if Bad nestthen 7 7: Pick thenest ni 8: Calculatte Lévy flightstep size α1←AG 99: PerformLévy flight frrom xito generate new eggxk 100: xi← xk 11:Fi←f( xi) 12: eend if 13: iif Top nest thhen 14:Pick the neest ni 15:Randomlypick another nnest njfrom another top ness t 16:if i = j thhen 17:Calculaate Lévy flighht step size α2←A G2 18:Performm Lévy flightfrom xito generate new egg xk 19:Fk=ff( xk) 20:else 22:Move ddistance dx froom the worst nest to the bes t nest tofind xk 23:Fk=ff( xk) 24:end if 25: eend if Algoorithm 3. MRMMCS on Reduuce 1: ddefinition: Reeducer (key, vvaluelist ): 2: iinput: (Last itteration fitness value, a population of n hhost nest Fi, i==1, 2,⋅⋅, n) 3: ffor all Fido 4:Find the beest value xbestoof Fi 5:Calculate ffitness Fi=f( xbest) 6: eend for In our experiiments, we immplemented bboth serial annd paraallel versionsfor MCS andd PSO on Haddoop. The seriial MCS generated thhe new egg of every nest aand replaced tthe oldegg with thhe better one serially. TThe processof MRMMCS was simmilar to the seerial MCS. Hoowever, instead of pperforming MMCS sequentiially, in ordeer to exchange information onHadoop, the3-egg-tupletransformation procceeded beforee executingthe mappingg and reducing funcctions. The ouutput of 3-egg--tuple transforrmation was the inpuut to the MapRReduce operattion. HHadoop carrried out asequence oof MapReduuce operrations, eachof which evaluated a sinngle iterationof MCS. In each MMapReduce opperation, Haddoop called tthe mappping functionn (as in Algorithm 2) annd the reducinng funcction (as in Allgorithm 3). MMappers in Haadoop generatted thenew egg of eevery nest thrrough the croossover or Lévvy flighht operation inn parallel andd reducers choose the best eggg fromm all candidattes of every nnest, respectivvely. The outpput of eeach MapReduuce operationn representedthe best eggof eachh nest. MRPSO was also immplemented aaccording to [4].Variious evaluatioons of MRMCCS and MRPSO in termsof perfformance andruntime weree compared inn the following sectiions. Experimentswere conduccted on a commputer withan AMD FX(tm)-8150 eight-coore processorr and 12 GB memory. Eighht virtual macchines (VMs)were run onn the phhysical machhine. A 10 Gdisk and a 11 G memorywere alllocated to eacch VM. Hadooop version 0.221 in Java 1.77 was used as the MMapReduce syystem for allexperiments.The innput dataset ((containing 10000 data nodees) was generated byy Latin hypeercube sampliing[9]with reespect to different appplications. HHere four eevaluation fuunctions andtwo engineeringoptimizationapplicationss[10]withtheir experimental reesults are pressented as folloows, respectively. The Griewannk function caan be expresseed as where in our eexperiment, dimension d iss set as 30, xiiis a raandom variablle, xi∈[-600, ++600], and i iis their indexfrom 1to d. Fig. 8compares thee performancee of MRMCSS and MMRPSO for GGriewank. As aa result, MRMMCS and MRRPSO foound the minnimum valuess at the scaleof 10-2and10-1affter 3000 times of iterationn evolution, ddemonstratingg that MMRMCS showws a faster convvergence thann MRPSO doees. Fig. 9 commpares the runntime of MRMMCS and MRRPSO onn Griewankusing 1, 2,4, and 8virtual machhines,reespectively. AAs you cansee, MRMCSS run fasterthan MMRPSO. Suchh phenomenoon can be aattributed totwo reeasons: 1) MRRPSO in [4] did not use fi tnness values askeys.AAs a result, inn each iteratioon, searchingthe optimal vvalue ammong all saamples requirres more timme for addittional coomparison operations. 2) MMRPSO requirres an extra fi lle for thhe dependentlist as its inpput data. Howwever, such alarge file incurs morre processingtime to the tootal runtime. MMore sppeci fi cally, inFig. 9, we caan also observve that the runntime off MRMCS deecreases whenn VM increaases. Althoughh the ruuntime reducttion is not linnear, MRMCCS still runs mmore eff fi ciently thann MRPSO doees on Hadoop. Define thee second evaluuation function—Rastrigrinas where in our eexperiment, ddimension d iss set as 30, xiiis a raandom variabble, xi∈[-5.122, +5.12], andd i is their iindex frrom 1 to d. Thhe performance comparisonn of MRMCSS and MMRPSO for Raastrigin is shoown in Fig. 100. Surprisinglyy, the mminimum valuue found by MMRMCS is mmuch smallerthan thhat found byy MRPSO aafter 3000 tiimes of iterration evvolution. Aggain, MRMMCS demonsstrates a better coonvergence tthan MRPSOO does. Runntime comparison beetween MRPSO and MRMMCS is pressented in Fig. 11.Similarly, thannks to two reeasons statedd above, MRMCS uses much shhorter runtimee than MRPSSO under vaarious numbers of VM in use. The total runtime used by MRMCS alsodecreases when the number of VM in use increases. Fig.8. Performance of MRMCS and MRPSO on Griewank. Fig.9. Runtime of MRMCS and MRPSO on Griew ank. Fig.10. Performanc e of MRMCS and MRPSO on Rastrigrin. Fig.11. Runtime of MRMCS and MRPSO on Ra strigrin. Fi g. 12. Performance of MRMCS and MRPSO on Rosenbroc k. Fi g. 13. Runtimee of MRMCS and MRPSO on Rosenbrock. The third eevaluation funcc tion, Rosenbrock, is define as where in our eexperiment, dimension d iss set as 30, xiiis a raandom variablle, xi∈[-100, ++100], and i iis their indexfrom 1to d. Fig. 122 compares thee performance of MRMCSS and MMRPSO forRosenbrock.In this casse, MRMCSand MMRPSO can fif nd the minimmum value off the same quuality affter 3000 timmes iterationevolution. However, MRMMCS coonverges durring the 5000th iterationwhere MRRPSO coonverges duriing the 1000thh iteration. Thherefore, MRMMCS iss more ef fi ciennt than MRPSSO in fi ndingthe optimalitty for RRosenbrock. Fig. 13 commpares the runntime of MRMMCS and MRRPSO onn Rosenbrockk using 1, 22, 4, and 8virtual machhines,reespectively. AAs you cansee, MRMCSS run fasterthan MMRPSO. Againn, MRPSO usses 2 to 3 times of runtimethan MMRMCS does,, demonstratinng that MCS iis more suitabble to bee parallelizedd on the MappReduce archiitecture thanPSO foor the functionn Rosenbrock. The expresssion of the Spphere function is w where in our experiment, dimension d is set as 30, xiis a random variable, xi∈[-5.12, +5.12], and i is their index fromm 1 to d. Fig.14 comparesthe performannce of MRMCCS andMRPSO forr Sphere. Unnlike previouss cases, in tthe midddle of the seaarch process,MRPSO oncee found a bettter valuue than MRMMCS duringaround the 4400th iteratioon.Howwever, it cannnot make anyadvancementt for the restof 26000 iterations.MRMCS, oon the other hand, keeps polishing it solutiion. Before thhe end of ourexperiment, we havee not yet cooncluded if thhe optimal vvalue found by MRMMCS is the truue minimum vvalue. AAs to the runttime, Fig. 15 ccompares it of MRMCS with MRPPSO to the Sphere functioon. Followingthe same trend as pprevious evaluuations, MRMMCS runs fasteer than MRPSO doess, maintainingg a 3 times speeed-up. Tensional andd/or compressional springsare used wideely in eengineering. TThere are thhree design vvariables in tthe sprinng design prooblem: the wirre diameter ww, the mean cooil diammeter d, and thhe length (ornumber of cooils) L. The goal is too minimize thhe weight of tthe spring witth the limitation of tthe maximumm shear stresss, minimumde fl ection, and geommetrical limitss. The detailsof spring desiign problem are desccribed in [11]and [12]. This overall pproblem can be formulated a s subj ect to wheere FFig. 16 and FFig. 17 showthe comparisson in termsof perfformance andd runtime oof MRMCSand MRPSO,resppectively, onthe spring deesign applicattion. It is cleear thatMRMCS andd MRPSO cann fi nd the samme optimal value butMRMCS ruuns much ffaster thanMRPSO doees,mainntaining a 4-tiimes speed-upp. Fig.14. Performanc e of MRMCS and MRPSO on Sphere. Fiig . 15. Runtimee of MRMCS annd MRPSO on Sphere. The Welded-beam design problemcomes fromm the sttandard tesst problemfor connstrained deesign opptimization[12],[13]. There arre four designn variables inn this prroblem: the wwidth w and leength L of thee welded areaa, the deepth d and thiickness h of tthe main beamm. The objectiive is too minimizethe overallfabricationcost, underthe apppropriate connstraints of thhe shear stresss τ, bending sstress σ, buckling loaad P(x), and mmaximum enddeflection δ. This overalll problem cann be formulateed as: suubject to where Fig. 18 and Fig. 19 show the performmance and runtime comparisons of MRMCS and MRPSO onn the welded-bbeam design application, respectively. Similaarly as the sppring design optimization, MRMCS and MRRPSO achievee the solutions of comparable quality whereasMRMCS only takes a quarter ofruntime thanMRPSO does. Fig.16. Performanc e of MRMCS and MRPSO on spring design. Fig.17. Runtime of MRMCS and MRPSO on spr ing design. Fig.18. Performance of MRMCS and MRPSO on welded-bea m design. Fig.19. Runtimeof MRMCS and MRPSO on welded-bea m design. Meta-heuristics as a search strategy for optimization has been extensively studied and applied to solve many engineering problems. Most of them suffer from long runtime and thus parallelizing them to improve their eff i ciency is a thriving topic in research. Recently, PSO has been successfully implemented on the MapReduce platform.Therefore, in this paper, we parallelize MCS on a MapReduce platform and propose MRMCS. Problems of job partitioning and information exchange are solved by modif i cation on the MapReuce architecture and 3-egg-tuple transformation. As a result, MRMCS outperforms MRPSO on four evaluation functions and two engineering design optimization applications. Experimental results show MRMCS has better convergence than MRPSO does.Moreover, MRMCS also brings about two to four times speed-ups for four evaluation functions and engineering design applications, demonstrating superior eff i ciency after parallelization on the MapReduce architecture (Hadoop). [1] J. Kennedy and R. Eberhart, “Particle swarm optimization,”in Proc. of IEEE Int. Conf. on Neural Networks, Perth, pp.1942–1948, 1995. [2] X. Yang and S. Deb, “Cuckoo search via Lévy fl ights,” in Proc. of IEEE World Congress on Nature & Biologically Inspired Computing, Coimbatore, 2009, pp. 210–214. [3] S. Walton, O. Hassan, K. Morgan, and M. Brown, “Modif i ed cuckoo search: a new gradient free optimisation algorithm,”Chaos, Solitons & Fractals, vol. 44, pp. 710–718, Sep.2011. [4] A. McNabb, C. Monson, and K. Seppi, “Parallel PSO using mapreduce,” in Proc. of IEEE Congress on Evolutionary Computation, Singapore, 2007, pp. 7–14. [5] J. Dean and S. Ghemawat, “Mapreduce: simplif i ed data processing on large clusters,” Communications of the ACM,vol. 51, no. 1, pp. 107–113, 2008. [6] W. Zhao, H. Ma, and Q. He, “Parallel k-means clustering based on mapreduce,” Lecture Notes in Computer Science vol. 5931, 2009, pp. 674-679. [7] I. Pavlyukevich, “Lévy fl ights, non-local search and simulated annealing,” Journal of Computational Physics,vol. 226, no. 2, pp. 1830–1844, 2007. [8] Hadoop: The Def i nitive Guide, O’Reilly Media, 2012. [9] R. L. Iman, “Latin hypercube sampling,” in Encyclopedia of Statistical Science Update, New York: Wiley, 1999, pp.408–411. [10] X. Yang and S. Deb, “Engineering optimisation by cuckoo search,” Int. Journal of Mathematical Modelling and Numerical Optimisation, vol. 1, no. 4, pp. 330–343, 2010. [11] J. S. Arora, Introduction to Optimum Design, Waltham:Academic Press, 2004. [12] L. Cagnina, S. Esquivel, and C. Coello, “Solving engineering optimization problems with the simple constrained particle swarm optimizer,” Informatica, vol. 32,no. 3, pp. 319–326, 2008. [13] K. Ragsdell and D. Phillips, “Optimal design of a class of welded structures using geometric programming,” ASME Journal of Engineering for Industries, vol. 98, no. 3, pp.1021–1025, 19763. MapReduce Architecture
3.1 Map Function (Mapper)

3.2 Reduce Function (Reducer)
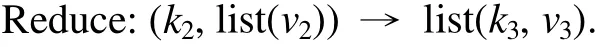
3.3 MapReduce Example
3.4 MapReduce Implementation
4. MRMCS
4.1 3-Egg-TupleTransformattion
4.2 MRMCS Maappers


4..3 MRMCS RReducers
5. Evaluations and Appl ications
5.1 Function GGriewank

5..2 Function RRastrigrin
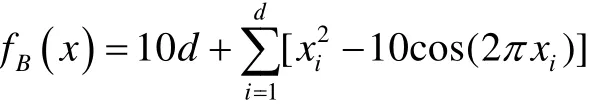




5.3 Function RRosenbrock

5..4 Function SSphere

5.5 Applicationof Spring Design

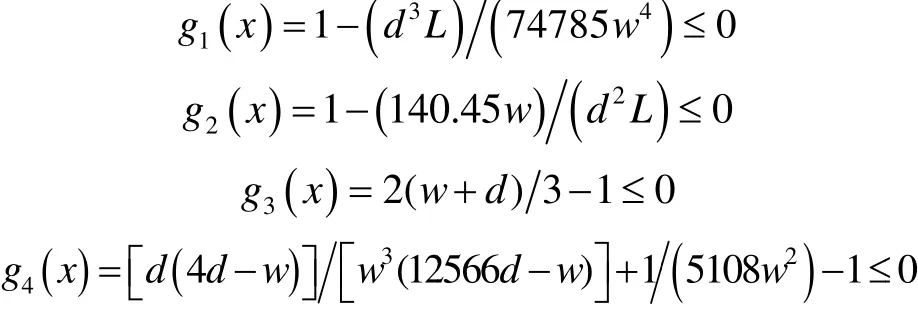
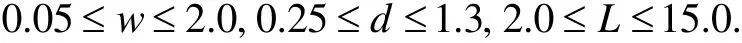

5..6 Applicatioo n of Welded--Beam Designn






6. Conclusions
杂志排行
Journal of Electronic Science and Technology的其它文章
- Design of a House Lease Management System in Cloud Computing
- Analysis of Key Attributes Influencing the User Satisfaction towards Applications
- Access Control Policy Analysis and Access Denial Method for Cloud Services
- A Unified Framework of the Cloud Computing Service Model
- ID-Based User Authentication Scheme for Cloud Computing
- Modified Packing Algorithm for Dynamic Energy-Saving in Cloud Computing Servers
