图像多角度局部特征提取及相似性匹配技术研究
2013-07-13徐望明石汉路
徐望明,石汉路
(武汉科技大学 信息科学与工程学院,湖北 武汉 430081)
图像特征提取是计算机视觉应用的根本基础。提取稳定而具有区分性的图像特征对于后续的一系列图像处理操作的效果具有重大的影响。图像的特征可分为全局特征和局部特征。由于全局特征难以应对图像畸变、遮挡、裁剪等情形导致其应用场合十分有限,近年来图像局部不变特征得以重视并飞速发展。然而,在大多数应用中,使用的是单一的局部特征。单一属性的局部特征只能描述图像某一方面的特性。局部特征的提取方法有多种,可以用多种性质互补的局部特征,即多角度局部特征,对图像内容形成多角度、更全面的描述。提取图像的多角度局部特征后,往往需要研究如何利用这些特征进行图像间相似性匹配,从而满足目标识别、图像检索等计算机视觉应用。基于稀疏编码的图像相似性匹配算法具有较少的空间与时间开销,能够适应大规模图像数据库的实时处理要求。
文中选取了SIFT、LBP、HOG这3种典型的图像局部特征作为多角度局部特征的实例,它们分别描述了图像的斑点区域特性、局部纹理特性和局部形状特性,结合基于稀疏编码的图像相似性匹配算法,并通过基于内容的图像检索实验验证了综合使用多角度局部特征相比单一局部特征能得到更高的检索正确率。
1 图像多角度局部特征提取算法
1)SIFT特征提取算法
SIFT(Scale Invariant Feature Transform,尺度不变特征变换)算法是David Lowe于2004年提出的一种对图像缩放、旋转、光照变化甚至遮挡和裁剪等保持不变性的特征提取算法。SIFT特征描述了图像的斑点(Blob)区域特性。
SIFT特征生成主要包括下面4个步骤[1-2]:
第1步:尺度空间极值检测。在高斯差分尺度空间中求出局部极值作为潜在的特征点。
第2步:精确定位特征点。去掉潜在特征点中的低对比度点和不稳定的边缘点,得到真正的特征点。
第3步:特征点方向分配。根据特征点邻域内点的梯度方向,为确定的特征点分配主方向。
第4步:生成特征描述向量。将特征点周围邻域分为4×4个子区域,对每个子区域在8个方向上进行梯度方向直方图统计得到4×4×8=128维的特征描述向量。
这样每幅图像可提取得到一个128维的SIFT特征矩阵。
2)LBP特征提取算法
LBP(local binary patterns,局部二值模式) 最初由 Ojala等人[3]提出,表述了灰度图像某像素点与周围像素点灰度值的大小关系。LBP算子描述了图像的局部纹理特性。原始的LBP算子定义在3×3窗口内,以窗口中心像素灰度值为阈值,将窗口内相邻的8个像素灰度进行二值化,按照一定的权值将二值化结果组成一个8位二进制数,即得该点的LBP值。像这样由整个图像可以得到一个对应的LBP响应图像,这个响应图像的直方图就是LBP特征。
为提高LBP特征的表达能力,Ojala等对原始的LBP特征进行扩展和改进。计算特征时不再局限于3×3窗口,而扩展到由参数R和P决定的圆域上,R和P分别代表设定的采样半径和圆周上的等间隔采样点数。为提高算子区分性,Ojala等提出了统一模式 (uniform patterns)LBP 特征 LBPu2D,R,在将对应的二进制位串视为循环串的情况下,如果串中包含的从0至1和从1至0的总的跳变次数不超过两次,则称它为统一模式。统一模式的意义在于,在LBP直方图计算过程中只为统一模式分配单独的直方图收集箱(bin),而所有非统一模式被放入一个公用收集箱中。
文中LBP采用的是取P=8,R=1时的Uniform(统一)模式LBP,对图像划分为若干小块后统计各块子区域内像素的LBP特征的统计直方图向量,统计时为全部的58个统一模式分配57个收集箱 (其中全0和全1放入同一收集箱),全部的非统一模式放入一个收集箱,共58个不同模式。最终每幅图像都得58维的LBP特征向量矩阵。
3)HOG特征提取算法
HOG (Histograms of Oriented Gradients, 梯度方向直方图)算法由法国的Dalal于2005年提出[4],目前它已经是目标检测领域里优秀的算法之一。HOG特征描述了图像的局部形状特性。
HOG算法的具体的实现方法是:首先将图像分成具有部分互相重叠的区间(Block),每个区间由 2×2 个单元(Cell)组成,每个单元(Cell)由若干像素区域组成(文中为10×10像素区域),然后计算这些区域中各像素点的梯度方向直方图并归一化,直方图将0~360°平分形成9个bin,这样每个区间(Block)被描述成一个4×9=36维向量,最后把这些直方图组合起来就构成了HOG特征向量矩阵。
2 基于稀疏编码的图像相似性匹配算法
经过局部特征提取后,图像的视觉内容由一组高维特征向量的集合来表示。图像数据内容的差异性导致各个向量集的大小是不同的。图像的相似性匹配问题转化为两个大小不一致的高维向量集的相似性匹配问题。在大规模图像数据库中,这些局部特征的数据数量十分庞大,直接利用它们进行图像相似性匹配将产生巨大的空间与时间开销。基于稀疏编码的图像相似性匹配算法,利用稀疏编码将图像的局部特征集转化为更高维的稀疏特征向量[5],然后通过计算稀疏向量之间的相似性(可由向量的距离函数来度量)得到图像之间的相似性,从而大大降低了时间与空间复杂度。
记 X=[x1,x2,…,xn] (xi∈Rd×1)为输入矩阵(每列是一个特征向量),表示d维空间中的一组包含n个局部特征向量的集合,即图像的“局部特征集”表示;B=[b1,b2,…,bn] (bi∈Rd×1)为基矩阵(每列是一个基向量),表示由k个基向量构成的视觉词典,可由训练图像学习得到;S=[s1,s2,…,sn](si∈RK×1)为系数矩阵(每列是一个系数向量),表示k利用视觉词典进行稀疏分解得到输入矩阵X的稀疏编码矩阵。则对特征向量的稀疏编码过程可以表示成下面的优化问题:
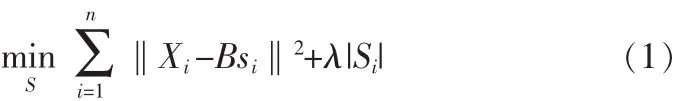
其中‖bk‖2≤1,k=1,2, …,K。 ‖Xi-Bsi‖2表示重构误差,|Si|是稀疏性的惩罚函数,λ为规则化参数,用于权衡重构误差和稀疏约束。
文中在此基础上,综合使用多角度局部特征,使之拥有更全面的图像信息表达能力。如图1所示,借助图像库提取得到的每种特征库进行训练得到的各自的视觉词典,分别为每个图像的局部特征矩阵进行稀疏编码,对得到的稀疏编码矩阵进行最大值合并(max pooling),从而得到同维度的高维特征向量。这样,每幅图像由提取得到的3种局部特征分别获取各自的稀疏特征sc_sift,sc_lbp,sc_hog,再按照一定的权重进行首尾相连能得到一个融合了多角度信息的稀疏特征向量sc_sift-lbp-hog。
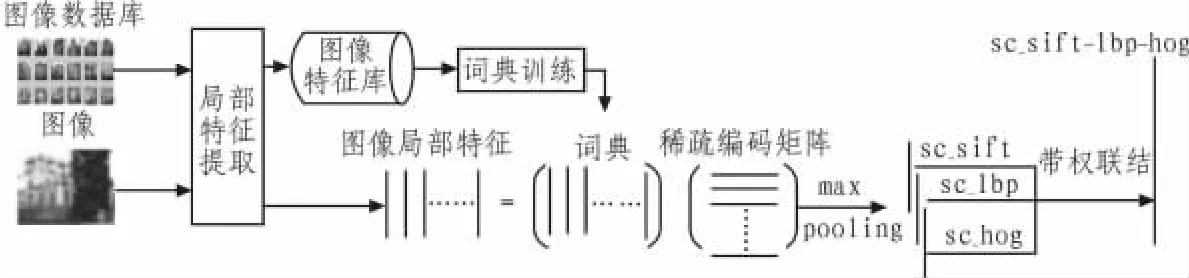
图1 稀疏特征向量形成过程示意图Fig.1 Schematic diagram of the forming process of sparse feature
这样,每幅图像能用一个包含图像多种局部信息的高维稀疏向量来描述。不同于直接进行图像局部特征之间的相似性匹配,此时图像的相似性匹配问题转化为向量之间的相似性匹配问题,可用向量的距离函数来衡量,距离越小越相似。用这个稀疏特征向量来描述图像的特征,相比单一特征对图像进行了更全面的描述,又具备全局特征的形式,因而这样的特征既具备了较强的图像局部信息描述能力,又能够适应大规模数据库中的图像处理要求。
3 基于稀疏编码的图像检索实验
实验时使用如图2所示的ZuBuD数据库[6]中全部的1 005幅图像作为数据库。ZuBuD库中共有201个不同场景,每个场景各有5张不同图片。每组各取一张图片,对201张图片对应的每种特征库进行采样smpN个向量进行训练,得到具有K个基向量的视觉词典。利用词典对全部的1 005张图片的特征矩阵进行编码,从而将每幅图像用一个K维的向量进行表示。然后,用向量间的距离来衡量图像之间的相似性程度。实验中取 smpN=20 000,K=1 024。
检索性能评价标准为查准率或查全率。对于一幅查询图像,定义n为检索出的相关图像数,T为检索出的总图像数,N为所有的相关图像数,则其查准率和查全率分别定义为:

图2 ZuBuD图像库中的图像示例Fig.2 Image examples in ZuBuD image database

根据ZuBuD库的特点,设定这里的T=N=5,故查准率与查全率是相等的,本文用平均查准率来衡量新特征用在检索上的准确性。将这1 005张图片逐个当作查询图像,进行5-近邻检索。分别计算3种特征单独编码检索和3种稀疏编码特征按一定权值联结得到的新特征检索的平均查准率。结果如表1和表2所示。

表1 单稀疏特征检索的平均查准率Tab.1 Average precision for single spares feature based retrieval

表2 多角度稀疏特征检索的平均查准率Tab.2 Average precision for multi-view sparse feature based retrieval
在文中实验条件下,新特征最高能取得75%的查准率,比其中任一单一特征的稀疏特征进行检索的平均查准率提高至少7%。由此可见,相比单一局部特征,综合利用多角度局部特征进行图像检索,能够得到更高的检索正确率。即多角度局部特征对图像局部信息具有更全面的描述与区分能力。
4 结束语
文中主要研究了SIFT、LBP、HOG等多角度图像局部特征提取算法以及基于稀疏编码的图像相似性匹配算法,在ZuBuD数据库上进行图像检索实验验证了算法有效性和高效性。研究结果表明:综合利用多角度局部特征,相比单一局部特征,能够更全面地描述图像信息;对提取的多角度局部特征进行稀疏编码,能获取表征图像本质内容的全局向量表示形式,同时具有全局特征和局部特征的优点;基于稀疏编码的图像相似性匹配算法,以一定的精度损失为代价,时间与空间开销很少,能够适应大规模图像数据库的实时处理要求。
[1]David G L.Distinctive image features from scale invariant keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[2]David G L.Object recognition from local scale-invariant features[C]//International Conference on Computer Vision,Washington,DC,USA:IEEE Computer Society,1999:1150-1157.
[3]Ojala T,Pietikinen M,Maenpaa T.Multiresolution gray scale and rotation invariant texture classification with local binary patterns[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):971-987.
[4]Dalal N,Triggs B.Histograms of oriented gradients for human detection[C]//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition,San Diego,CA,USA,2005:886-893.
[5]Yang Jian-chao,Yu Kai,Gong Yi-hong,et al.Linear spatial pyramid matching using sparse coding for image classification[C]//IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL,2009:1794-1801
[6]ZuBuD Image Database[EB/OL].[2012-08-20].http://www.vision.ee.ethz.ch/showroom/zubud.
