三塔斜拉桥地震响应分析
2013-07-13赵娟娟
赵娟娟
(天津铁道职业技术学院,天津 300240)
一、工程概况
济南建邦黄河大桥位于济南市西北部老徐庄附近,主桥采用三塔斜拉桥,跨度布置为53.5+56.5+2×300+56.5+53.5m=820m共6跨连续结构,整幅布置。三塔采用不等高形式布置,中塔高于两边塔。边跨长110m,中跨长300m,如图1所示。边塔采用塔、梁分离,主梁开8×4.5m的孔洞供边塔塔柱穿过,中塔采用塔、梁、墩固结体系。桩基础为摩擦桩,中塔桩长110m,边塔桩长100m,桩直径2m。

图1 三塔斜拉桥总体布置图(单位:m)
二、空间有限元模型的建立
模型A采用空间梁单元模拟,共计梁单元454个,节点597个。边塔和主梁交接处有竖向主从约束,中塔、梁、墩固结。边塔和中塔墩底固结。

图2 模型B
模型B是在模型A基础上建立承台、桩和土弹簧单元形成的,如图2所示。共计梁单元1273个,节点1498个,桩底固结。桩土的相互作用用等代土弹簧模拟[1],土弹簧刚度k的确定采用“m法”[2]。
三、动力特性分析
对模型A和模型B均采用Lanczos法分析了桥梁结构动力特性,表1分别列出了两模型的前十阶自振频率和振型的主要特征,图3给出了模型B的部分振型图。

表1 模型A和模型B的动力特性比较

图3 模型B前四阶振型图
通过分析表1,可知:
1)模型B的自振频率均小于模型A的自振频率,说明考虑桩土效应后,结构体系变柔。
2)在模型A和模型B中,中塔横弯都出现较早,说明中塔横向刚度较小,应采取措施加大中塔横向刚度。
3)模型B中,边塔横弯比主梁对称竖弯较早出现,中塔在第七阶出现二阶横弯,说明考虑桩土效应之后,边塔和中塔的横向刚度都减弱。
4)主梁竖弯在两模型前十阶振型中占到50%,就该斜拉桥来说,主梁的竖向刚度都偏小。
四、地震响应分析
1.地震动参数[3]
根据《中国地震动参数区划图》并结合新实行的《公路桥梁抗震设计细则》,查得桥位处场地抗震设防烈度为7度,水平向设计基本地震加速度峰值为0.1g,设计特征周期为0.45s,由于场地类别为Ⅲ类,周期调整为0.65s,结构阻尼比为ξ=0.05。计算中分别考虑:顺桥向+竖向、横桥向+竖向两个工况。动力分析取前300阶。
2.反应谱曲线
水平设计加速度反应谱最大值[3]为:

式(1)中,Ci=1.0为抗震重要性系数,Cs=1.3为场地系数,Cd=1为阻尼调整系数,A=0.1g为水平向设计基本地震加速度峰值。
水平设计加速度反应谱曲线由下式确定:

式(2)中,Sa(T)为水平设计加速度反应谱,T为结构自振周期,Tg为特征周期。水平向设计加速度反应谱如图4所示。竖向地震动加速度峰值取为水平地震动加速度峰值的0.5倍[3]。
3.加速度时程曲线[4]
正确的地震加速度时程曲线,应该满足频谱特性、加速度峰值和持续时间这三个要素的要求。由于缺少该场地地震波历史记录和人工地震波,按照三要素要求,选取三条与桥址场地相符的地震波记录,即EL-Centro波(270°)、EL-Centro波(180°)和EL-Centro波(vertical)[5]并分别将地震波峰值加速度调整为0.1g.

图4 E1作用下水平向设计加速度反应谱

图5 地面加速度时程样本一
五、动力计算结果
1.反应谱分析
通过反应谱分析,得出两种工况下的最大内力和最大相对位移,表格中内力响应为局部坐标方向,取相应数值的绝对值最大值,位移响应为整体坐标方向,取正负位移绝对值最大值,计算结果见表2-4:

表2 结构内力响应峰值(纵+竖)

表3 结构内力响应峰值(横+竖)
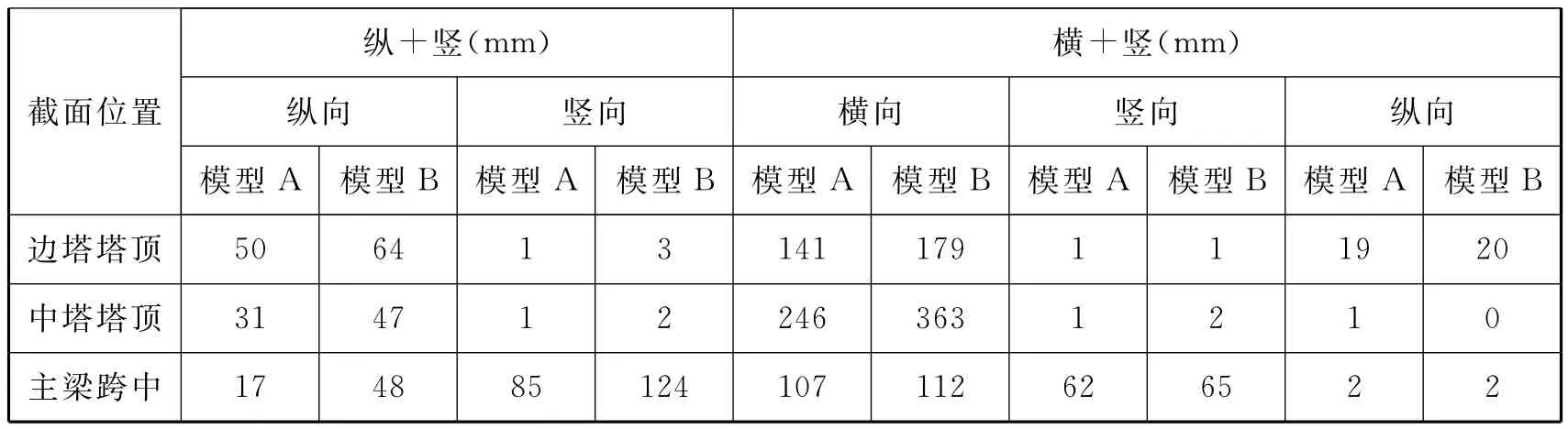
表4 结构位移响应峰值
从表2-4可知:
1)无论是在纵+竖输入还是横+竖输入下,中塔根部的剪力和弯矩远远大于边塔根部,这是由于中塔采用塔墩梁固结的方式,中塔墩刚度很大,导致分配到的内力就大,这对抗震很不利。
2)在纵+竖输入下,模型A与模型B轴力相差不大,但模型A的剪力和弯矩都大于模型B。
3)在横+竖输入下,模型A与模型B轴力相差不大,但模型A的剪力和弯矩都小于模型B。
4)对于塔来说,塔在纵+竖输入下产生的内力大于在横+竖输入下产生的内力,对主梁来说,主梁在纵+竖输入下产生的弯矩小于在横+竖下产生的弯矩,这点在抗震设计中要引起重视。
5)在纵+竖输入下,边塔和主梁横向位移不明显,但在横+竖输入下,除产生横向和竖向位移外,边塔纵向位移明显,这是由边塔左右索力不对称所致,中塔纵向位移很小,因为中塔左右索力对称。
6)无论是在纵+竖输入还是横+竖输入下,模型B产生的位移都比模型A产生的位移要大,这是由于考虑了桩土效应后,结构变柔,基本周期变大,位移响应更明显,特别是中塔两模型位移相差较大,这是由于中塔柱要高于边塔,塔顶位移响应更明显。
2.时程分析
在两种地震工况的激励下,获得结构在El波作用下的时间历程反应,时程分析结果采用每个工况下的最大值。模型B中塔弯矩时程曲线和中塔塔顶位移时程如图6-7所示。

表5 结构内力响应峰值(纵+竖)
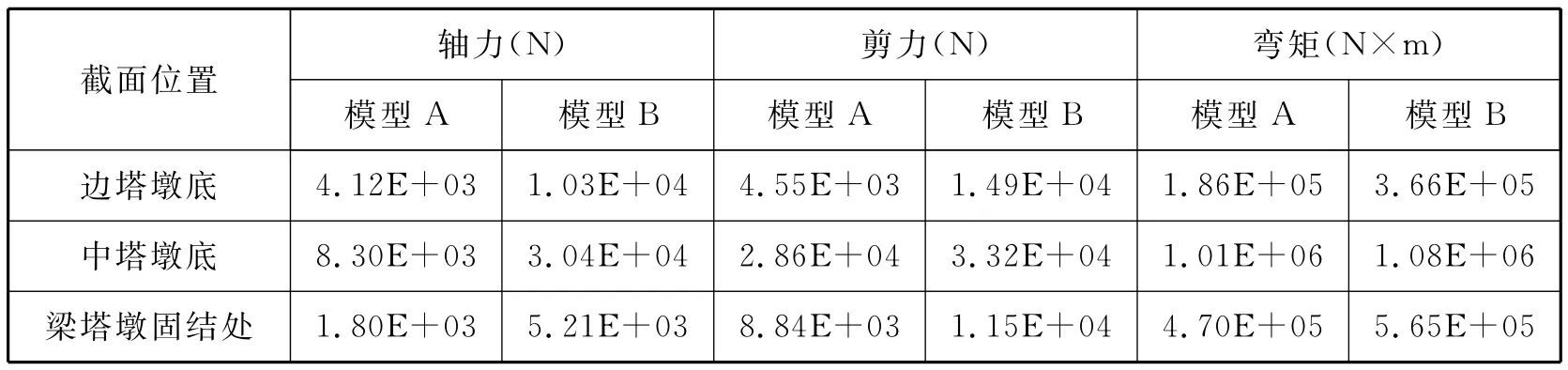
表6 结构内力响应峰值(横+竖)
从表5-6可知:
在两种工况下,除模型B轴力比模型A轴力较大外,弹性时程分析内力结果的规律同反应谱分析内力结果趋势一致,且时程计算值在反应谱法计算值上下波动,故时程分析可用于对反应谱的校核,反应谱法可用于初始设计阶段的截面验算。

图6 模型B中塔弯矩时程曲线(纵+竖)

图7 模型B中塔塔顶纵向位移时程曲线(纵+竖)
由图6-7可知,在纵+竖向地震波作用下,桥塔根部的弯矩时程曲线和中塔顶部的位移时程曲线呈明显的周期性变化,随时间的延续,趋于平缓。
六、结论
对于桩基础为摩擦桩且桩长较长的桥梁,考虑桩土效应,相对于不考虑桩土效应,结构的频率减小,基本周期变大,地震位移响应变大。在进行抗震分析时,需要考虑桩土效益。
在纵+竖输入下,模型B的剪力和弯矩较模型A减小,在横+竖输入下,模型B的剪力和弯矩较模型A增大,说明考虑桩土效应后内力变化有大有小,所以在分析大跨度斜拉桥抗震时,考虑桩土效应更能反映桥梁实际结构受力。为使结构设计安全合理,应该考虑桩土效应。
[1]范立础,胡世德,叶爱君.大跨度桥梁抗震设计[J].北京:人民交通,2001,(03).
[2]范立础.桥梁抗震[M].上海:同济大学出版社,1996.
[3]公路桥梁抗震设计细则(JTG/T B02-01-2008).
[4]李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,1992.
