双环Petersen网络直径公式及最优路由算法

魏葆雅，刘日华，陈宝兴

1.漳州师范学院 计算机科学与工程系，福建 漳州 3630002.江西教育学院 数学与计算机科学系，南昌 330032

双环Petersen网络直径公式及最优路由算法

魏葆雅1，刘日华2，陈宝兴1

1.漳州师范学院 计算机科学与工程系，福建 漳州 363000
2.江西教育学院 数学与计算机科学系，南昌 330032

1 引言

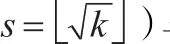
2 DLCPG（k）的直径公式

从下面的定理1可以看出文献[5]中的性质2有误，性质2给出的双环Petersen网络DLCPG(k)的直径为（其中为向上取整操作符）。

下面先给出同余方程的最小非负解与最小交叉解的定义。设s是一个整数，1≤s＜k。

定义1称(a1，a2)是同余方程

的非负解，如果a1+a2s≡0(modk)，a1≥0，a2≥0且(a1，a2)≠(0，0)。称(u，v)是同余方程（1）的最小非负解，如果(u，v)是同余方程（1）的非负解且满足以下条件：

（1）如果(a1，a2)是同余方程（1）的非负解，则u+v≤a1+a2。

（2）如果(a1，a2)是同余方程（1）的非负解，且(a1，a2)≠(u，v)，a1+a2=u+v，则u＞a1。

例如，容易验证（4，1），（2，3），（0，5），（8，2），（4，6），…是同余方程 x+6y≡0(mod10)的非负解，而（4，1）是方程x+6y≡0(mod10)的最小非负解。

定义2设(u，v)是同余方程（1）的最小非负解。称(-a1，a2)是同余方程（1）的交叉解，如果-a1+a2s≡0(modk)，a1≥0，a2≥0，(-a1，a2)≠(0，0)，且三个坐标点(-a1，a2)，（0，0），(u，v)不在同一直线上。称(-a，b)是同余方程（1）的最小交叉解，如果(-a，b)是同余方程（1）的交叉解且满足以下条件：

（1）如果(-a1，a2)是同余方程（1）的交叉解，则a+b≤a1+a2。

（2）如果(-a1，a2)是同余方程（1）的交叉解，且(-a1，a2)≠(-a，b)，a1+a2=a+b，则b＞a2。

例如，容易验证（2，2）是同余方程x+5y≡0(mod12)的最小非负解，且（-5，1），（-3，3），（-1，5），（-12，0），（-10，2），（-8，4），…是同余方程x+5y≡0(mod12)的交叉解，而（-1，5）是同余方程x+5y≡0(mod12)的最小交叉解。

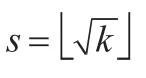
引理1设s是一个大于或等于2的整数。

（1）当k=s2时，同余方程（1）的最小非负解与最小交叉解分别为(0，s)与(-s，1)。

（2）当s2＜k＜s2+s时，即k=s2+r，1≤r＜s，同余方程（1）的最小非负解与最小交叉解分别为(r，s)与(-s，1)。

（3）当k=s2+s时，同余方程（1）的最小非负解与最小交叉解分别为(0，s+1)与(-s，1)。

（4）当s2+s＜k＜s2+2s时，即k=s2+s+r，1≤r＜s，同余方程（1）的最小非负解与最小交叉解分别为(r，s+1)与(-s，1)。

（5）当k=s2+2s时，同余方程（1）的最小非负解与最小交叉解分别为(0，s+2)与(-s，1)。

证明 现在就情形（4）给予证明，其余类似可证。先证(r，s+1)是同余方程（1）的最小非负解。

设(p，q)是同余方程（1）的非负解，分3种情形讨论：

（1）当 p＜r时，必有 q＞s+1（否则，0＜p+qs＜r+ (s+1)s=k，这与(p，q)是同余方程（1）的非负解矛盾）。因为s+p-r+(q-s-2)s≡0(modk)且0＜s+p-r＜s，所以有q-s-2＞s。可知 p+q≥q＞2s+2＞r+s+1。

（2）当 p=r时，必有 q≥s+1（否则，0＜p+qs＜r+ (s+1)s=k，这与(p，q)是同余方程（1）的非负解矛盾）。可知p+q≥r+s+1。

（3）当 p＞r时，考虑4种子情形。

①当q=0时，有p=tk，t≥1，此时p+q＞r+s+1。

②当q=1时，有p=s2+r+tk，t≥0，此时p+q＞r+s+1。

③当1＜q＜s+1时，则必有 p≥s+r（否则，0＜p+qs＜ r+s+s×s=k，这与(p，q)是同余方程（1）的非负解矛盾）。因此有 p+q＞r+s+1。

④当q≥s+1时，有 p+q＞r+s+1。

由上可知当(p，q)≠(r，s+1)时，必有 p+q＞r+s+1。由定义可知(r，s+1)是同余方程（1）的最小非负解。

现证(-s，1)是同余方程（1）的最小交叉解。

设(-p，q)是同余方程（1）的交叉解，分3种情形讨论：

（1）当q=0时，有 p=tk，t≥1，此时p+q＞s+1。

（2）当 q=1时，则由 -p+s≡0(modk)，可得 p-s≡0(modk)，即p=tk+s，t≥0，可知 p+q≥s+1。

（3）当q＞1时，考虑3种子情形。

①当p=0时，必有q≥s+2（否则，0＜-p+qs≤(s+1)s＜k，这与 (-p，q)是同余方程（1）的交叉解矛盾），此时p+q＞s+1。

②当1≤p＜s时，必有 q≥s+1（否则，0＜-p+qs≤-p+s×s＜r+s+s2=k，这与(-p，q)是同余方程（1）的交叉解矛盾），此时 p+q＞s+1。

③当 p≥s时，有 p+q＞s+1。

由上可知当(-p，q)≠(-s，1)时，必有 p+q＞s+1。由定义可知(-s，1)是同余方程（1）的最小交叉解。证毕。

由引理1可得下面的推论。

推论 设k，s是正整数，s≥2，k=ps+q，p≥1，0≤q＜s。当s2≤k≤s2+2s时，同余方程（1）的最小非负解与最小交叉解分别为(q，p)与(-s，1)。

引理2设s是一个大于或等于2的整数。用d记双环网络G(k;±1，±s)的直径。

（1）当k=s2时，d=s-1。

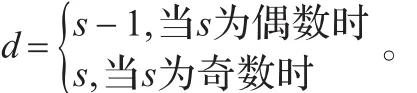
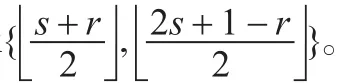
（4）当k=s2+s时，d=s。

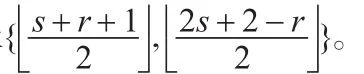
（6）当k=s2+2s时，d=s。

证明 现在就情形（5）给予证明，其余类似可证。由引理1可知当k=s2+s+r，1≤r＜s，同余方程（1）的最小非负解与最小交叉解分别为(r，s+1)与(-s，1)。

由引理2可得下面的定理1。

定理1设s是一个大于或等于2的整数。用D记双环Petersen网络DLCPG(k)的直径。

（1）当k=s2时，D=s+1。

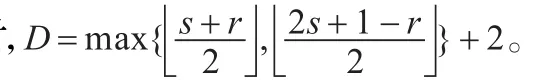
（4）当k=s2+s时，D=s+2。

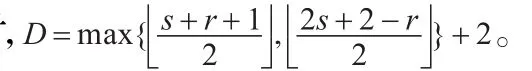
（6）当k=s2+2s时，D=s+2。

3 DLCPG（k）的最优单播路由算法

对于无向双环网络G(k;±1，±s)，从点i到点(i+1)(modk)的边称为[+1]边，点i到点(i-1)(modk)的边称为[-1]边，点i到点(i+s)(modk)的边称为[+s]边，点i到点(i-s)(modk)的边称为[-s]边。若一条从点i到点 j的路径，它包含x1条[+1]边，x2条[-1]边，y1条[+s]边，y2条[-s]边，则有j≡(i+x1-x2+y1s-y2s)(modk)，且等式成立与路径中边的顺序无关，故可将此路径记为x1[+1]+x2[-1]+y1[+s]+y2[-s]。

性质1设 x1[+1]+x2[-1]+y1[+s]+y2[-s]是一条从i到j的最短路径，则x1与x2至少有一个为0，y1与 y2至少有一个为0。

从性质1知从i到 j的最短路径使用的边仅含[+1]边与[+s]边，或仅含[-1]边与[+s]边，或仅含[+1]边与[-s]边，或仅含[-1]边与[-s]边。为了方便起见，把路径x1[±1]+ x2[±s]用(±x1)[+1]+(±x2)[+s]表示。比如用6[+1]+(-3)[+7]表示6[+1]+3[-7]。

路由算法是影响计算机网络通信的重要因素。文献[5]给出了DLCPG(k)的单播路由算法，然而此算法所找到的路径一般情况下并不是最短的。例如：按照文献[5]的算法（2），2），无向双环网络G(9 950;±1，±99)中从节点0到节点4408应走的路径为(-47)[+1]+45[+99]，其路径长度为92。事实上按照下面所给的算法Routing Algorithm for G(k;±1，±s)，找到的最短路径为2[+1]+56[-99]，其长度为58。

利用文献[1，7]所得的结论，直接给出无向双环网络G(k;±1，±s)的一个路由算法，此路由算法是最优的，文献[1]已就其一般情形进行严格证明。欲求从节点i到节点j的最短路径，只需求出从节点0到节点(j-i)(modk)的最短路径。为讨论方便起见，以下总设节点0为源节点。

Routing Algorithm forG(k;±1，±s)：利用引理1，可以得到同余式x+ys≡0(modk)的最小非负解(u，v)与最小交叉解(-a，b)。下面的算法将给出从0到t的最短路径。

这里[( x，y)]=([x]，[y])，[x]表示对x进行四舍五入得到的整数。

步骤2 P1:=a1[+1]+b1[+s]

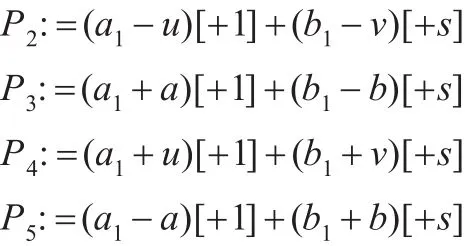
P1，P2，P3，P4，P5这5条路径中的最短者就是从节点0到节点t的最短路径。

例1找出无向双环网络G(9 950;±1，±99)中从节点0到节点4408的最短路径。

因为9 950=992+99+50，利用引理1，（4）的结论：同余方程（1）的最小非负解与最小交叉解分别为(50,100)与(-99，1)。由算法的步骤1：

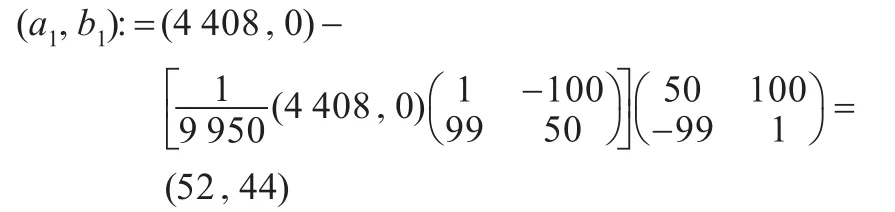
步骤2：

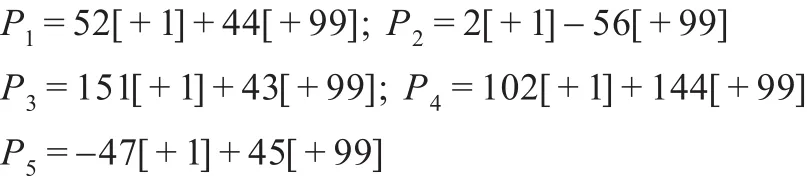
所以从节点0到节点4408的最短路径为P2=2[+1]-56[+99],其长度为58。

利用上面的路由算法Routing Algorithm forG(k; ±1，±s)，给出DLCPG(k)的一个最优路由算法。假设节点A(Ar，Ap)向节点B(Br，Bp)发送数据。

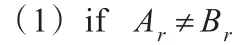
{利用上面的算法Routing Algorithm forG(k;±1，±s)，找出从0到(Br-Ar)(mod k)的最短路径，即可找到从A(Ar，Ap)到节点C(Br，Ap)的最短路径。}

（2）ifAp=Bp，结束。

Else ifC(Br，Ap)与B(Br，Bp)是相邻节点，可以直接通信。

Else通过公共的相邻节点进行通信。

因为双环Petersen图互联网络DLCPG(k)是双环网络与Petersen图的笛卡尔积，且上面算法的第一步是双环网络G(k;±1，±s)的最优路由算法，第二步是Petersen图的最优路由算法，所以所给的算法是DLCPG(k)网络的一个最优路由算法。下面举一例予以说明。

例2求 DLCPG(9 950)中从节点 (7，aaaaaa)到节点 (4415，baab00)的最短路径（参见文献[5]中图2的Petersen图）。

根据算法第一步，利用算法Routing Algorithm for G(k;±1，±s)，找出从双环网络G(9 950;±1，±99)中从0到4408的最短路径为2[+1]-56[+99]。如此找到了从节点(7，aaaaaa)到节点(4415，aaaaaa)的最短路径。

此时节点 (4415，aaaaaa)与 (4415，baab00)在同一Petersen图。因为aaaaaa≠baab00，从Petersen图知baaa00 是aaaaaa与baab00的公共邻点，所以有(4415，aaaaaa)—＞(4415，baaa00)—＞(4415，baab00)。

综上可知从节点(7，v1)到节点(4415，u2)的最短路径为：(7，aaaaaa)—＞(8，aaaaaa)—＞(9，aaaaaa)—＞(9860，aaaaaa)—＞(9761，aaaaaa)—＞(9662，aaaaaa)—＞…—＞(4415，aaaaaa)—＞(4415，baaa00)—＞(4415，baab00)，路径长度为60。

4 结论

本文给出了双环Petersen图互联网DLCPG(k)的直径显式公式，并利用x+ys≡0(modk)的最小非负解与最小交叉解给出了网络DLCPG(k)的一个简单且最优的单播路由算法，并用例子予以说明。

[1]Chen B X，Meng J X，Xiao W J.A constant time optimal routing algorithm for undirected double-loop networks[C]// MSN'05.Berlin：Springer-Verlag，2005，3794：308-316.

[2]王雷，林亚平.基于超立方体环连接的Petersen图互联网络研究[J].计算机学报，2005，28（3）：409-413.

[3]OhringS，DasS K.FoldedPetersencubenetworks：new competitors for the hypercubes[J].IEEE Transactions on Parallel and Distributed Systems，1996，7（2）：151-168.

[4]刘方爱，刘志勇，乔香珍.一种实用的互连网络RP（k）及其路由算法[J].中国科学：F辑，2001，44（6）：461-473.

[5]王雷，林亚平，夏巍.双环Petersen图互联网络及路由算法[J].软件学报，2006，17（5）：1115-1123.

[6]Chen B X，Meng J X，Xiao W J.A diameter formula for an undirected double-loop network[J].Ars Combinatoria，2009，90：395-404.

[7]钟玮，陈宝兴，朱素钦.无向双环网络的新直径公式[J].计算机工程与应用，2010，46（32）：84-87.

WEI Baoya1,LIU Rihua2,CHEN Baoxing1

1.Department of Computer Science and Engineering,Zhangzhou Normal University,Zhangzhou,Fujian 363000,China
2.Department of Mathematics and Computer Science,Jiangxi Institute of Education,Nanchang 330032,China

The Double-Loops Connected Petersen Graph network DLCPG（k）is Cartesian product of a double-loop network and the Petersen graph.It has good extensibility,short diameter and simple topology structure.By studying its topology structure,the diameter formula of DLCPG（k）is obtained,and a simple and optimal routing algorithm for the DLCPG（k）is given.

interconnection networks;diameter;double-loops connected Petersen graph;optimal routing

双环Petersen图互联网络DLCPG（k）是双环网络与Petersen图的笛卡尔积，它具有良好的可扩展性、较短的网络直径和简单的拓扑结构等特性。通过研究其拓扑结构，得到了DLCPG（k）直径的显式公式，并给出了该网络的最优单播路由算法。

互联网络；直径；双环Petersen图；最优路由

A

TP393

10.3778/j.issn.1002-8331.1207-0295

WEI Baoya,LIU Rihua,CHEN Baoxing.Diameter formula and optimal routing algorithm for double-loops Petersen networks.Computer Engineering and Applications,2013,49（5）：81-83.

国家自然科学基金（No.60973150）；福建省自然科学基金（No.2010J01354）。

魏葆雅（1981—），女，讲师，主要研究领域为计算机网络、算法设计与分析；刘日华（1963—），男，副教授，主要研究领域为算法设计与分析；陈宝兴（1961—），男，博士，教授，主要研究领域为计算机网络、算法设计与分析。E-mail：tinawby@hotmail.com

2012-07-20

2012-12-03

1002-8331（2013）05-0081-03