基于演化博弈的农民工返乡创业研究
2013-07-11董文波杜建国
董文波,杜建国,2,任 娟
(1.江苏大学 管理学院,江苏 镇江212013; 2.南京大学 工程管理学院,江苏 南京210093)
一、引 言
农民工是我国特有的城乡二元体制的产物,是我国在特殊历史时期出现的一个特殊社会群体,根据国家统计局《2011年我国农民工调查监测报告》显示,2011年全国农民工总量达到25278万人。然而,近年来,大批农民工集中返乡的现象引起了社会的高度关注。影响农民工回流的影响因素众多,主要包括:受金融危机影响,国外对我国劳动密集型产品需求降低,农民工就业岗位减少;城市的生活成本过高;中央对“三农”问题的高度关注,并出台了一系列支农、惠农、强农的政策等。正确认识“民工潮回流”现象,鼓励和支持返乡农民工创业,以创业带动就业,以创业推动经济发展,使其成为新农村建设的积极力量是解决返乡农民工问题的新思路,具有重要的经济和社会意义。
返乡农民工创业具有一定的优势,其中包括: 农民工打工期间开阔了视野、扩大了知识面,通过工作的磨练掌握了一定的生产技术;与从事传统农业相比,农民工的收入较为可观,具备一定的创业物质基础;返乡农民工务工期间建立了较为广泛的人际关系网,掌握一定的社会资源等[1]。然而,返乡农民工创业也面临着诸多依靠个人力量难以克服的困难和问题,影响着创业的成功,具体表现为:政府支持力度不够,缺乏正确引导;创业融资困难,得不到金融机构的支持;农村创业教育与培训力度不够等[2]。因此,如何有效利用返乡农民工创业的优势,规避其创业过程中的障碍,是各地政府亟需重视和解决的问题。
在返乡农民工创业过程中,存在当地政府和农民工两个主体,双方博弈关系明显。为了解返乡农民工创业过程中博弈双方的演化机制,本文将在分析影响当地政府和返乡农民工主体行为因素的基础上,构建返乡农民工创业过程中博弈双方行为交互的演化博弈模型,分析相关情形下模型的均衡点和稳定性,基于相关参数变动对模型演化结果的影响提出改善建议。
演化博弈论源于生物进化理论,是将博弈理论分析与动态演化过程相结合的一种理论。在解释社会习惯、规范和制度的自发形成及其影响因素方面取得了众多成绩[3-8]。该方法以参与群体为研究对象,假设参与主体具有有限理性,参与人的行为是动态调整的过程,弥补了经典博弈论方法的局限性。本文将在演化博弈模型分析的基础上探讨引导系统良性演化的方法,以期为返乡农民工创业问题的研究提供一个新的视角。
二、农民工返乡创业的演化模型
(一)模型假设
本文根据地方政府和返乡农民工群体之间的策略及收益关系构建博弈模型,根据动态复制方程研究博弈双方的行为演化。地方政府的策略空间为S1{支持,不支持},返乡农民工的策略空间为S2{创业,不创业},博弈双方均为有限理性。为了更好地描述双方的收益支付关系,做如下假设:
(1)地方政府的正常收益为R,当其支持返乡农民工创业时将付出一定的支持成本,记作C1,当然,返乡农民工通过创业能够给当地政府带来一定的收益,记为r;当其不支持农民工创业时C1=0。
(2)在当地政府的支持下,返乡农民工选择创业的最大预期收益为E1,其付出的创业成本为C2;当政府不支持返乡农民工创业时,其选择创业的成本将会增加,记作C3,C3>C2。同时,由于缺乏当地政府的支持,返乡农民工创业的预期收益将会受到影响,记作vE1,其中0 <v <1。同样,给当地政府带来的效益也将受到影响,为vr。
(3)当返乡农民工不选择返乡创业时,将继续从事一般性的就业活动,获得正常收益E2,E1>E2。
根据上述变量的定义,本文可以构建出地方政府和返乡农民工群体双方的博弈矩阵,如表1 所示。

表1 当地政府与返乡农民工策略支付矩阵
其中,E1>E2,C3>C2,0 <v <1。
(二)模型的演化
假设在初始状态下,当地政府采取“支持”策略的比例为p,采取“不支持”的比例则为1-p;农民工选择“创业”的比例为q,选择“不创业”策略的比例为1-q,下面将计算博弈双方的期望收益及平均收益。
U1为当地政府选择“支持”策略的期望收益,U2为当地政府选择“不支持”策略的期望收益为当地政府的平均收益。

同理,V1为农民工选择“创业”策略的期望收益,V2为农民工选择“不创业”策略的期望收益。为农民工的平均收益。

根据Malthusian 动态方程,策略的增长率等于其对应的适应度[9-10],得出当地政府群体和农民工群体策略交往随时间演化的动力学方程,如(1)所示。
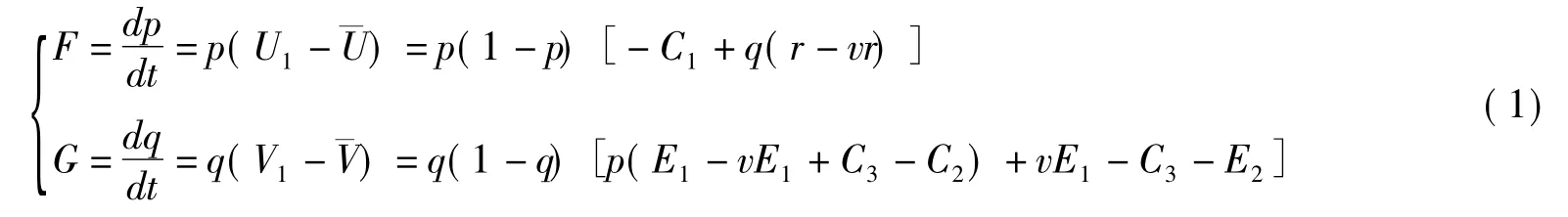
根据Firedman 提出的方法,演化系统均衡点的稳定性可由该系统的雅克比矩阵的局部稳定性分析得到。根据方程(1),可求得相应的雅克比矩阵J,以及雅克比矩阵J 的行列式DetJ、迹Tr。其中

三、模型分析
(一)均衡点及其稳定性分析
演化稳定策略( Ess)表示具有思考能力的有限理性主体,在博弈过程中根据其既得收益对行为策略进行调整以追求更佳的收益,最终形成的一种动态平衡[11]。根据上述的复制动态方程(1)可知,当时,当地政府群体中使用“支持”策略所占比例是稳定的; 当q =0,1 或p =时,农民工群体中选择“创业”策略的农民工所占比例是稳定的。由于p、q分别表示博弈双方群体中选择某一策略的个体所占比例,因此有0≤p≤1,0≤q≤1,从而本文将在M={( p,q)|0≤p≤1,0≤q≤1}的平面上讨论系统方程的均衡点及稳定性,由及可得约束条件为C1<(1-v)r 且vE1-C3<E2<E1-C2。在此约束前提下,该系统有5个局部平衡点,根据雅克比矩阵的局部稳定分析法对这5个均衡点进行分析,具体如表2 所示。

表2 局部稳定分析结果
从局部稳定分析中可知,5个均衡点中有两个为Ess,分别对应于当地政府和返乡农民工博弈过程中两个极端的模式,即:当地政府支持、返乡农民工创业;或当地政府不支持、返乡农民工不创业。(0,1)、(1,0)为不平衡点为鞍点。这三点的折线是系统收敛于不同模式的临界线,折线左侧区域为收敛于不良模式的概率,右侧区域为收敛于理想模式的概率。由鞍点的表达式可知,相关参数变动会引起鞍点的移动,从而起到调控演化方向的作用。图1 显示了当地政府与返乡农民工交往的动态过程。

图1 当地政府和返乡农民工交往的动态过程
(二)参数分析及系统相图
本文下面将分析当地政府的获益r、当地政府的支持成本C1、返乡农民工创业的收益E1及返乡农民工创业成本C2等参数变动对演化结果的影响,并绘制相应的相图。绘制相图时,需分析及在相平面上的符号表示轨线的水平分量p( t)增加,且鞍点水平向右移动0 时鞍点会水平向左移动。同理,当时,分量q( t)增加,鞍点垂直向上移动;而时鞍点垂直向下移动。
(1)农民工创业给当地政府带来的收益r。由鞍点表达式可知0。这表明当农民工通过创业能够给当地政府带来更高的收益时,图1 中的鞍点垂直下降( 见图2( b)),使得区域面积SNMHL增加,从而系统收敛到理想状态的可能性提高。现实社会生活中,返乡农民工的创业实践能够为农村创造就业岗位,推动经济发展,促进农村工业化进程,当地政府从中所获的收益r 显著。
(2)当地政府支持农民工创业的成本C1。在鞍点M( p*,q*)处有当地政府的支持成本过高时,鞍点会垂直向上移动( 见图2( a)),使得收敛于良好状态( 支持,创业)的概率降低,从而不利于系统的良性演化,因此,科学合理的政策措施才能保证支持机制的长期有效运行。
(5)其他参数分析方法类似,本文不做进一步阐述。

图2 (a)参数C1 增加、r 减小
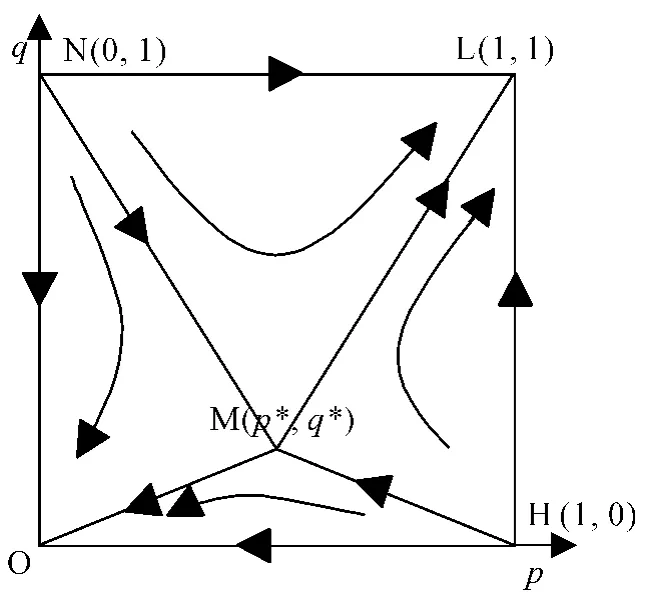
图2 (b)参数r 增加、C1 减少

图3 (a)参数E1 增加、C2,C3,E2 减小
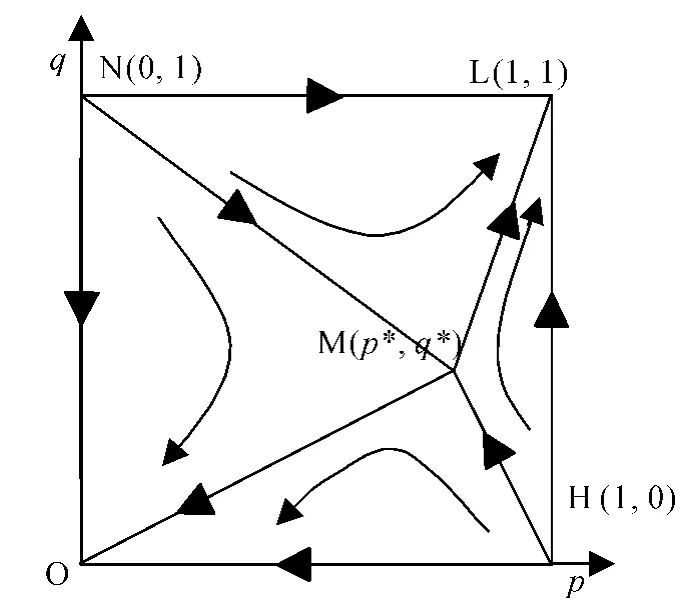
图3 (b)参数C2,C3,E2 增加、E1 减小
四、建议与结论
根据相位图( 见图2、3)的变动规律可知,要引导系统朝良好模式演化就需调节相关参数大小,使得区域面积SNMHL增大。因此,本文针对现实中返乡农民工创业面临的主要问题,从降低返乡农民工创业成本,保障其收益等方面就如何推动农民工返乡创业问题提出建议措施。
(1)提高地方政府对返乡农民工创业工作的重视力度。地方政府应认识到返乡农民工创业实践在促进地方经济发展、提升工业化水平、推进城镇化进程,加快新农村建设等方面的重要意义,这也意味着返乡农民工的创业实践能够为地方政府创造可观的收益r。因此,地方政府需通过强化服务意识、放宽创业准入条件、简化审批程序、加强基础设施建设等措施,切实解决返乡农民工创业过程中面临的难题,保障创业活动的顺利开展,从而在提高地方政府收益r 的同时,降低了返乡农民工创业的成本,确保农民工的创业收益E1,形成博弈双方共赢的良性局面。
(2)完善金融服务,加大财政和税收扶持力度。如:为返乡创业农民工提供便利的信贷服务,降低融资成本;对返乡创业农民工的提供鼓励性的创业补贴,提高创业积极性;对农民工创办的企业给予税收方面的优惠,减轻负担等。只有开辟多渠道的支持方案,才能有效降低返乡农民工的创业成本,提高其创业积极性,保障返乡农民工创业机制的长期有效运行。
(3)重视对返乡农民工创业的教育培训和技术支持力度。为了进一步提高返乡农民工的创业意愿,提升其创业能力,各地政府需加大对返乡农民工的教育培训和技术支持力度。通过整合资源,为农民工提供便捷的创业培训和指导,使其能够对宏观经济、市场行情以及现代管理经验等方面有更好的认识,从而形成“造血式”创业扶持模式,这种模式不仅能够避免“输血式”模式造成C1的过高成本压力,而且能够对返乡农民工创业氛围的营造和维持起到至关重要的作用。
本文借助演化博弈理论对返乡农民工创业问题进行了探讨,得出系统收敛于两种模式,一种为当地政府支持、农民工创业的理想模式; 另一种是当地政府不支持、农民工不创业的不良模式,这两种模式都为演化稳定策略。因此引导系统朝理想模式演化,避免锁定于不良模式就必须采取措施调节相关参数的影响程度。本文通过演化博弈模型分析及绘制相位图,直观展示了农民工返乡创业过程中相关参数对演化机制的影响,并就理论分析结果提出了相关改进建议,为返乡农民工创业问题的研究提供了一个新的视角。当然,文中所涉及的相关参数实际影响效果还有待进一步的实证研究,我们会在下一步的研究中继续完善。
[1]杨仁德,向 华,魏善元.返乡农民工就业与新农村建设: 贵州返乡农民工就业的思考[J]. 贵州农业科学,2009,37(3): 178-181.
[2]孙富安.公共服务视角下回流农民工创业影响因素及应对方略[J]. 经济经纬,2010,(5):67-71.
[3]梅 强,马国建,杜建国.中小企业信用担保路径演化研究[J]. 系统工程学报,2009,24(3):280-285.
[4]梅 强,马国建,杜建国.中小企业安全生产管制路径演化研究[J].中国管理科学,2009,17(2): 160-168.
[5]任玉珑,刘 贞,粟增德,曹 杨.发电企业经营博弈过程中的效仿行为仿真研究[J].系统工程理论与实践,2006,26(11):46-52.
[6]李洪波,杨 兰,杜建国,等.基于演化博弈的大学生诚信考试研究[J]. 数学的实践与认识,2010,40(12):33-45.
[7]张苏荣,王文平.基于知识更新的企业合作演化博弈分析[J]. 软科学,2011,25(1):24-27.
[8]盛昭瀚,高 洁,杜建国.基于NW 模型的新熊彼特式产业动态演化模型[J]. 管理科学学报,2007,10(1):1-8.
[9]FRIEDMAN D.Evolutionary games in economics[J]. Economical,1991,59(3):637-666.
[10]盛昭翰,蒋德鹏.演化经济学[M].上海:上海三联书店,2002.
[11]HODGSON G.Economics and evolution: bring life back to economics[M].Cambridge: Polity Press,1993.
