基于AHP和灰色理论的登陆作战效能评估*
2013-07-11胡峥涛钟兴军
胡峥涛 钟兴军,2 谢 勇
(1.海军装备研究院标准规范研究所 上海 200235)(2.上海交通大学 上海 200240)
1 引言
登陆作战是对敌方海岸地带或岛、礁的渡海背水进攻作战。登陆作战通常包括以下四个阶段,即集结上船、海上航渡、突击上陆、巩固和扩大登陆场,前两个阶段的任务主要是由水面舰艇编队来完成,这两个阶段的作战效能可以理解为水面舰艇编队的作战效能。由于不同阶段所使用的主战兵力不同,评估的方法也有区别,因此,本文所论述的登陆作战主要是指在水面舰艇编队夺取了一定的海上优势后进行的联合抢滩登陆作战。在有些登陆作战效能评估中,主要考虑作战部队的静态效能,即仅考虑武器装备对作战效能的固有影响,不考虑人员训练水平、心理素质以及指挥员的指挥能力等影响作战效能的人为因素。为此,本文将作战中的主观与客观因素相结合,对登陆作战效能进行评估。
2 影响登陆作战效能的因素和指标体系建立
2.1 影响作战效能的主要因素[1~2]
登陆作战效能主要由以下因素决定:一是登陆部队生存能力。为了达成登陆任务的目的,必须使登陆部队(包括武器装备)生存下来,否则登陆无法完成。二是指挥与协同作战能力。正确、及时、连续的指挥是夺取登陆作战胜利的重要环节,为了使登陆部队发挥出整体功能,还必须把握整体性原则,将所有登陆部队中的陆、海、空三军联合起来,将所有传感器、武器系统统一协调起来形成合力。三是作战保障能力。及时为登陆部队提供信息、情报、资源、火力、工程、后勤和技术保障是登陆部队发挥作战效能的前提。四是战场环境适应能力。登陆战场不仅地理条件复杂,而且还处于复杂电磁环境和敌人火力攻击范围中,因此登陆部队必须具有良好的抵御和适应能力。
2.2 建立登陆作战效能指标体系
根据以上分析,建立登陆作战效能指标体系如图1所示。
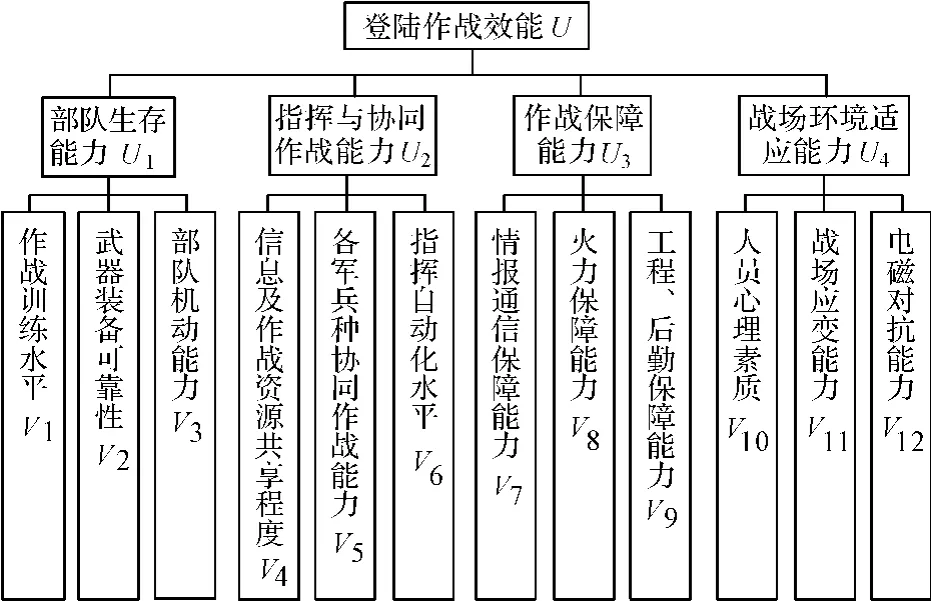
图1 登陆部队作战效能的指标体系
3 使用AHP法确定每个因素集中各子因素的权重[3~5]
层次分析法(The Analytic Hierarchy Process简称AHP法)是20世纪70年代由美国运筹学家T.L.Saaty提出的一种决策分析方法。它是一种定性与定量相结合的多目标决策分析方法,适用于解决结构比较复杂、决策准则较多且不易量化的决策问题。在本文中,为了表示登陆作战效能中各指标因素的相对关系,给不同的因素赋予不同的权重,采用AHP法确定权重,可以将决策者的专业知识和经验判断充分给予量化,克服其它方法的弊端。
现在以指标体系中第一层子目标为例,建立和求解判断矩阵,确定这一组四个因素的相对重要性或相对价值。构造两两比较的判断矩阵,判断矩阵中的各元素数据来自军事专家调查数据的统计分析,该矩阵元素满足T.L.Saaty提出的1—9标度,其判断矩阵A(相对于登陆作战效能而言各因素之间相对重要性的比较)如下:

3.1 计算判断矩阵的最大特征值和特征向量
计算最大特征值λmax和特征向量的方法有很多,这里采用方根法求解判断矩阵A的特征值,并确定子因素权重数值的大小。具体步骤如下:
1)计算矩阵A中每一行元素乘积的n次方根βi:

2)对向量β= (β1,β2,…,βn) 进行归一化处理:
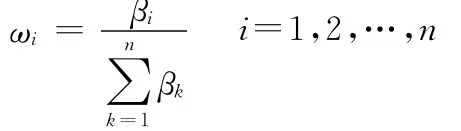
得向 量ω= (0.4690,0.3137,0.1376,0.0797)T即 为 所 求的特征向量。
3)计算矩阵A的最大特征根λmax:
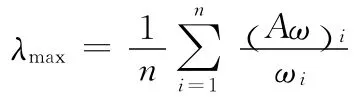
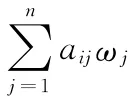
3.2 判断矩阵的一致性检验
理想的判断矩阵应满足aij=aik/ajk,i,j,k=1,2,…,n;同时有λmax=n,其余特征根为0。但是,由于客观事物的复杂性和某种程度上的模糊性,靠直觉和判断力不可避免地带有估计误差,因此,这样构造出来的判断矩阵通常不可能具备完全一致性,只能说近似地具备一致性。下面对判断矩阵进行判断。
1)计算判断的一致性检验指标CI:
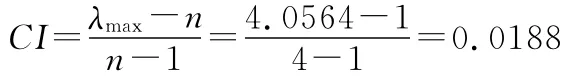
2)确定平均一致性指标RI。平均一致性指标是每次重复进行随机判断矩阵特征值计算之后取算术平均值得到的。多级矩阵的平均随机一致性指标见表1。

表1 多级矩阵的平均随机一致性指标
3)根据随机一致性比率检查判断矩阵是否具有满意的一致性
随机一致性比率为判断矩阵的一致性指标和同级平均随机一致性指标之比。若CR=CI/RI≤0.1,判断矩阵RI具有满意的一致性指标;否则需要重新调整判断矩阵。当n=4时,有RI=0.90,CR=0.0188/0.9=0.021<0.1,所以判断矩阵具有满意的一致性指标。
采用2.1的方法,可得第二层指标体系权重,亦可计算出CR1=0.0091、CR2=0.0268、CR3=0.0192、CR4=0.0091,均<0.1,判断矩阵A1,A2,A3,A4都具有满意的一致性。
3.3 计算最底层元素对于目标的合成权重
1)计算第二层子目标相对于总目标的权重系数wij=Wij·ωi
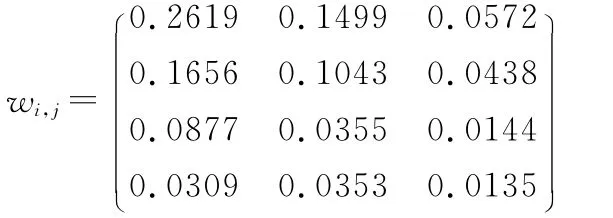
2)底层元素相对于目标的合成权重
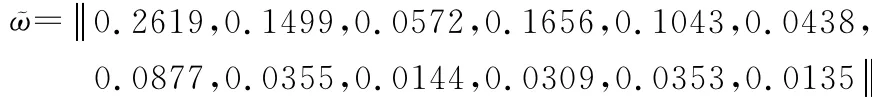
4 运用灰色评估法评估[4]
4.1 求指标的评估样本矩阵
指标体系中最底层有m=12个评估指标,假设有p=4个专家参与评估,第k(k=1,2,3,4) 个评估者对于第i(i=1,2,…,12) 个评估指标给出的评分是dik,得到如下评估样本矩阵D:

4.2 确定评估类
确定评估类就是要确定评估灰类的等级数,灰类的灰数以及灰数的白化权函数,针对具体对象,通过定性分析确定。
本文主要采用以下两种形式的白化权函数:
1)灰度数为⊗∈[0,d1,∞),其白化权函数为
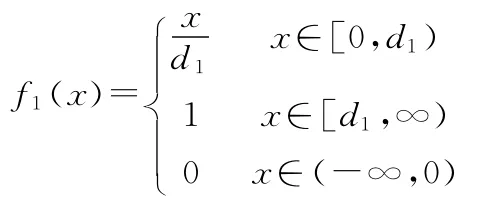
2)灰度数为⊗∈[0,d1,d2),其白化权函数为
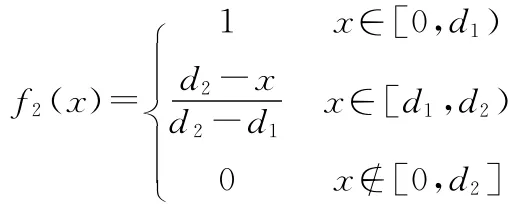
在对登陆作战效能评估中,将指标的评分等级划分为优、良、中、差四个等级,对应四个评估灰类,即N=1,2,3,4,其相应的灰数及白化权函数如下:
N=1,设定灰数⊗1∈[0,9,∞),白化权函数为f1,如图2所示;
N=1,设定灰数⊗2∈[0,7,10],白化权函数为f2,如图3所示;
N=1,设定灰数⊗3∈[0,4,8],白化权函数为f3,如图4所示;
N=1,设定灰数⊗4∈[0,2,6],白化权函数为f4,如图5所示;
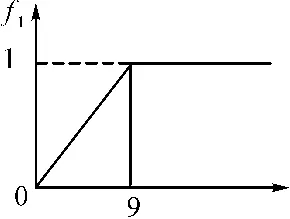
图2 白化权函数f1
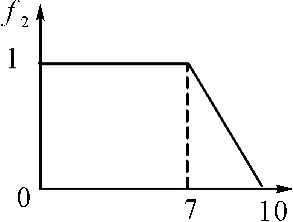
图3 白化权函数f2
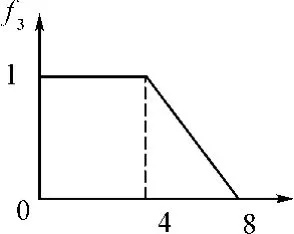
图4 白化权函数f3

图5 白化权函数f4
4.3 计算灰色评估系数、灰色评估权重
对于评估指标Vi,第N(N=1,2,3,4)个评估灰类的灰色评估系数记为xi,N,评估灰类的总灰色评估系数记为xi,属于第N个评估灰类的灰色评估权记为ri,N,则
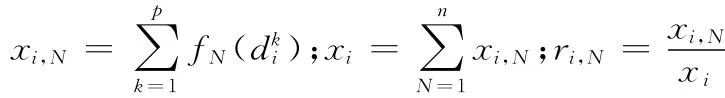
对于评估指标V1(作战训练水平),其四个评估灰类的灰色评估系数分别为

则指标V1相对各个评估灰类的总评估系数x1为

指标V1属于四个评估灰类的灰色评估权重分别为

同理可求得指标V1,V2,…,V12的灰色评估权重矩阵为

4.4 计算综合聚类系数,给出评估结果
设评估对象关于第N个灰类的综合聚类系数为σN,则
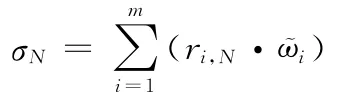
登陆作战效能关于四个灰类的综合聚类系数分别为

5 结语
本文运用AHP结合灰色系统的原理和方法,建立了登陆作战效能的评估模型,模型中采用AHP确定登陆作战效能各评估指标的权重,应用灰色评估法进行信息的量化和比较,评估采取定量分析为主,与定性分析相结合。评估结果证明,层次分析法与灰色评估相结合能有效降低人为因素的影响,评价结果具有客观性,一定程度上能给决策者提供可靠的判断依据。
[1]杨世幸,陈松辉.登陆作战概论[M].北京:海潮出版社,2002.
[2]刘万年,徐振邦.登陆作战纵横谈[M].北京:海潮出版社,1995.
[3]李策,马开城,刘树立.军事运筹基本方法[M].北京:解放军出版社,2004.
[4]邓聚龙.灰色系统理论教程[M].武汉:华中工学院出版社,1990.
[5]邢利华,刘式宋.炮兵精确打击指挥信息系统作战效能评估[J].计算机与数字工程,2010(1).
[6]栾孝丰,温瑞.基于UML和ADC法的舰载反舰导弹武器系统效能评估[J].计算机与数字工程,2010(8).
[7]张卓,刘伊林.作战效能评估[M].北京:军事科学出版社,1996.
