薄壁轴承套圈在旋转气场中的自定位分析
2013-07-10王晓强刘宇峰崔凤奎张兆龙
王晓强,刘宇峰,崔凤奎,张兆龙
(1.河南科技大学机电工程学院,河南洛阳471003;2.匹兹堡州立大学,美国匹兹堡66762)
0 引言
薄壁套圈轴承是尺寸系列中壁厚最薄的一种轴承,由于其精度高、摩擦因数小、噪声低以及极限转速高等优点,广泛应用于模型飞机、机床、电机及纺织机械等产品。薄壁轴承套圈尺寸一般有D/d1≤1.143 或D/d2≤1.340,如图1 所示。此类轴承内外套圈的内径或外径尺寸较大,壁厚尺寸小于四分之一内径,且小于两倍滚动体直径[1]。在一个系列的薄壁轴承中,采用保持恒定的横截面尺寸,与其内径无关;而常规球轴承系列中,径向横截面及球径一般与其内径尺寸呈正比关系。薄壁轴承以其极轻的质量和不随孔径增大而增大的小横截面而引人瞩目[2]。相对于常规大型及重载轴承,薄壁轴承还具有更严格的配合公差。因此,薄壁轴承经常被推荐用于需要精确控制或者旋转轴拆卸位置苛刻的地方。传统的轴承套圈检测方法一般是用机械夹持方式进行定位,并采用接触式测头进行检测。这种定位及测量方式极易使薄壁轴承套圈产生变形,无法实现精确测量。此问题一直是困扰国内轴承行业实现薄壁轴承套圈精密测量的一大难题。采用电磁无心夹具和支撑配合的装夹方式,目前多用于大中型轴承外径加工中,不适合成品轴承套圈装夹及检测[3-5]。文献[6]提出采用多对气动测量装置,能有效地对薄壁轴承套圈进行检测,但需对套圈进行初定位。因此,要实现薄壁轴承套圈的精确测量,首先要解决对薄壁轴承套圈的精确定位。本文提出利用旋转稳定气场实现薄壁轴承套圈自定位的方法,并对薄壁轴承套圈在旋转气场作用下的变形及受力进行分析与评价。

图1 薄壁轴承套圈结构示意图
1 旋转气场定位原理
在薄壁轴承套圈的检测中,为防止定位力导致轴承套圈产生变形,一般可采取电磁装夹、气动定位等方法。电磁装夹在检测后需对零件进行消磁处理,主要用于非成品的检测[3]。本文根据薄壁轴承套圈质量小、易变形的特点,提出了在套圈内部产生稳定气场,由气场压力实现零件自定位的技术方案。此方法与传统装夹定位方式相比,同样定位力下压强很小,能有效防止被测零件产生变形。
图2 为旋转气场定位方案的结构原理示意图。整个装置是以喷气式旋翼中心为中心位置,其工作原理为:高压气体经进气道顶端开口处进入喷气式旋翼气道,并由旋翼末端喷气口高速射出;因气体的反作用力使旋翼产生旋转,在旋翼旋转过程中喷气口气体持续稳定射出,形成旋转稳定气场。若轴承套圈中心与气场中心不重合,套圈因内壁受到非均布压力产生位移,套圈中心与气场中心之间的距离逐渐减小,直到零件中心与气场中心重合为止,从而达到轴承套圈自动定心的目的。根据整体测量技术方案的要求,定位装置允许套圈轴线与气场中心最大偏距为2 mm。

图2 喷气式旋翼自定心结构示意图
2 流固耦合数值模拟
为准确获得套圈内壁的表面周向应力分布及套圈变形情况[7-10],本文采用ANSYS 与FLUENT 相结合,通过流场耦合模态求解的方式获得套圈内壁压力,分析得出最佳的气场输出压力值。
2.1 流固耦合方式
ANSYS+FLUENT 耦合方法利用ANSYS 软件包中强大的结构分析模块,采用有限单元法的基本思想进行结构分析,同时,利用FLUENT 进行模拟和分析集合区域内的流体流动。这种耦合方法借助了两大软件各自的优势,通过用户自定义功能(UDF)接口程序将两者连接起来,在流固耦合场中进行稳态求解,相互迭代,直到收敛[11-12]。
ANSYS+FLUENT 耦合流程(如图3 所示)为:
(1)根据旋转气场定位对薄壁轴承套圈定位的实际情况,抽象出相应的力学模型,并确定其几何参数。(2)利用PRO/E 软件建立流体模型和固体模型,并分别划分流体、固体模型网格设置边界条件,实现耦合面的匹配。(3)设置流体域计算收敛标准,进行稳态计算,达到收敛解。(4)将经运算收敛后的交界面上的结点力作为边界条件,通过接口程序施加到固体边界结点上,在ANSYS 的Static Structural 模块中进行有限元静力分析并导出固体中流固耦合面的结点位移文件,将其传递给FLUENT,使用动网格技术重构并更新网格,再进行流场的稳态计算,如此往复计算直至流体域与固体域均达到收敛标准,在计算过程中分别采用边界结点力和位移作为收敛标准。

图3 双向流固耦合流程图
2.2 模型建立及耦合条件设置
在流体入口压力不变的情况下,对壁厚为3 mm、直径Di分别为80 mm、90 mm、100 mm、110 mm、120 mm 的系列轴承套圈进行有限元求解,计算出套圈变形大小及受力变化趋势。设定套圈偏心距(轴承套圈轴线与气场中心轴线间距离)选取范围为2 ~20 mm,节距2 mm,共10个节点来进行计算分析。建立几何模型如图4 所示,外部为被测轴承套圈模型,内部为定位气场模型。
在ANSYS 中添加轴承套圈材料为滚动轴承钢,其参数如表1 所示。在FLUENT 中设置流体模型参数条件,设置如表2 所示。
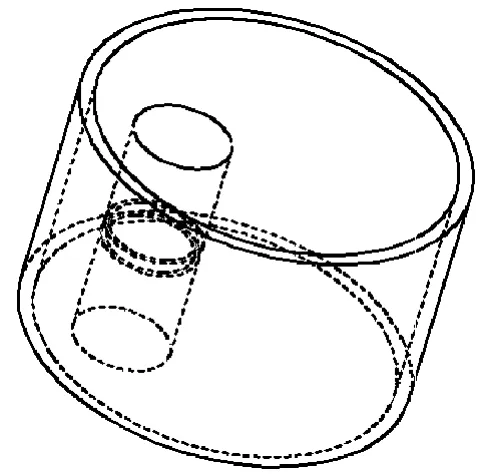
图4 轴承套圈与内部气场模型

表1 滚动轴承钢材料参数
表2 流体模型边界条件
套圈与气场接触面定义为Fluid Solid Interface(流固耦合面)。流体材料选择理想不可压缩气,FLUENT 流体模型中,上下两底面定义类型为Pressure Outlet(压力出口);其进口类型定义为Pressure Inlet(压力入口);其余默认定义为Wall(壁面)。Mesh Motion(网格运动类型)设置如下:Option 选ANSYS MultiField(多场分析)选项,Receive from ANSYS 选Total Mesh Displacement(网格总位移)选项,Send to ANSYS 选Total Force(总压力)选项。
2.3 耦合求解结果
图5 为流体部分压强分布图,图6 所示为套圈变形情况。从图5 和图6 中可以看出:流体压强在旋翼与轴承套圈偏心方向上中间部分最大,与方案制定预期结果一致。从图6 中可以看到套圈变形情况与流体压强分布一致。

图5 流体部分压强分布图
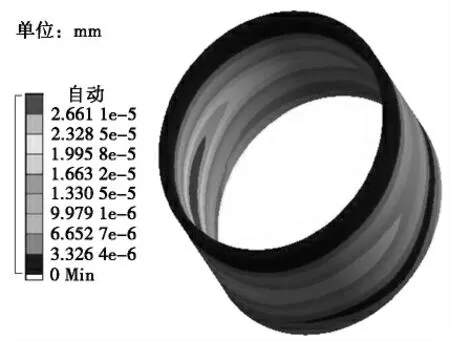
图6 套圈变形图
3 流固耦合结果分析
从软件中导出5 组直径的轴承套圈试验数据,如表3 所示。其表明在对该系列薄壁套圈定位时,直径为80 mm 的套圈,在其轴线与气场中心轴线偏距20 mm 时受到最大应力为21.696 kPa,其最大应力远远小于其屈服极限;薄壁轴承套圈在偏距2 mm 时所受旋转气场最小推力为0.857 4 N,套圈与大理石底座产生的静摩擦力为0.83 N,故可得出:当旋翼出口压力为一个大气压时,所形成气场产生的推力足以对套圈进行中心定位并不会产生塑性变形。
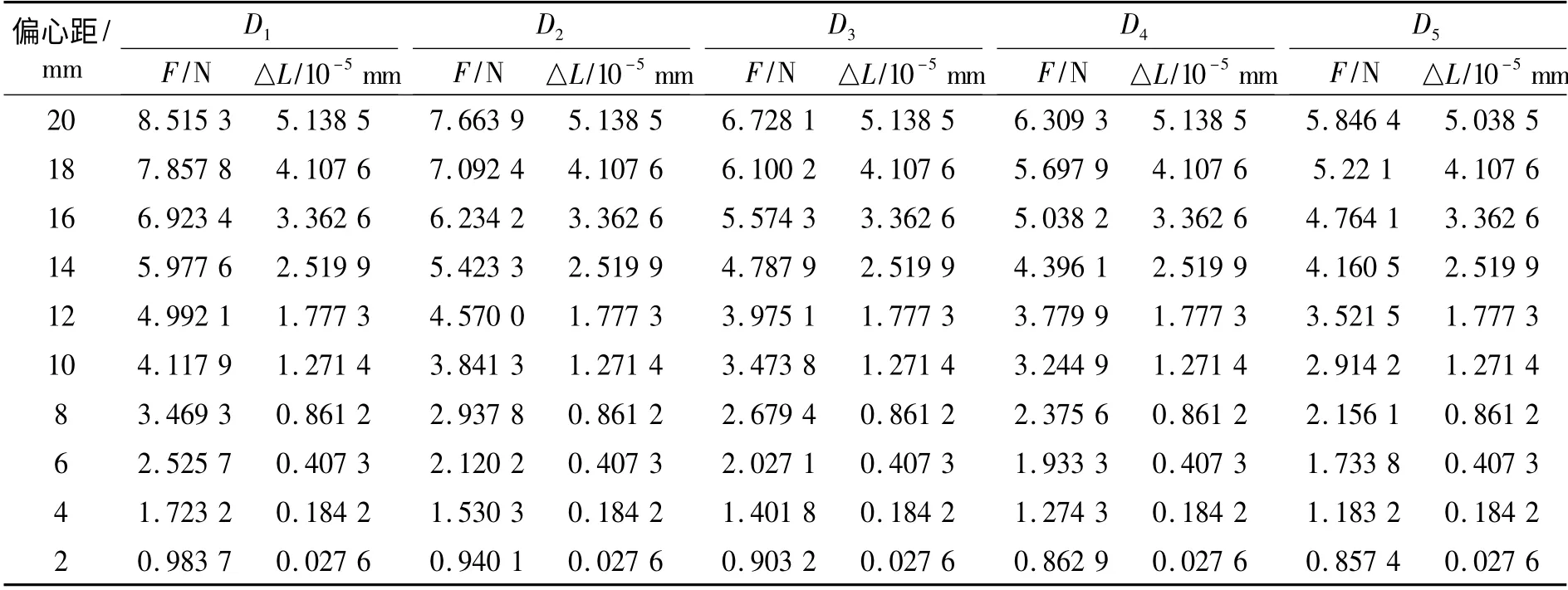
表3 套圈所受推力与变形量数据表
图7 为在不同的偏心距(套圈中心与气场中心距离)下,由于气场压差产生的推力变化曲线。该推力F 与偏心距d 呈线性关系,如图7 所示对两者进行线性拟合,其拟合数据结果见表4,方程式为:

其中,ki为各个拟合直线斜率,d 为偏心距,a1为拟合直线方程截距。当偏心距为0 时,轴承套圈受力为0,故拟合直线方程截距a1=0。对方程(1)中各拟合直线斜率ki与套圈直径Di做线性拟合,其拟合方程式为:

综合以上分析,在影响套圈所受推力F 的因素中只考虑套圈直径与偏心距时,可将方程(1)和方程(2)联立得:

从而可以得出:当旋翼出口压力一定时,对于已知直径的轴承套圈,在旋转气场中所受推力F 大小与偏心距d 呈式(3)所表述的线性正比关系。根据式(3),即可判定能否对某尺寸轴承套圈进行自定位并求出定位精度(推力F 大于轴承静摩擦力时的d 值)。
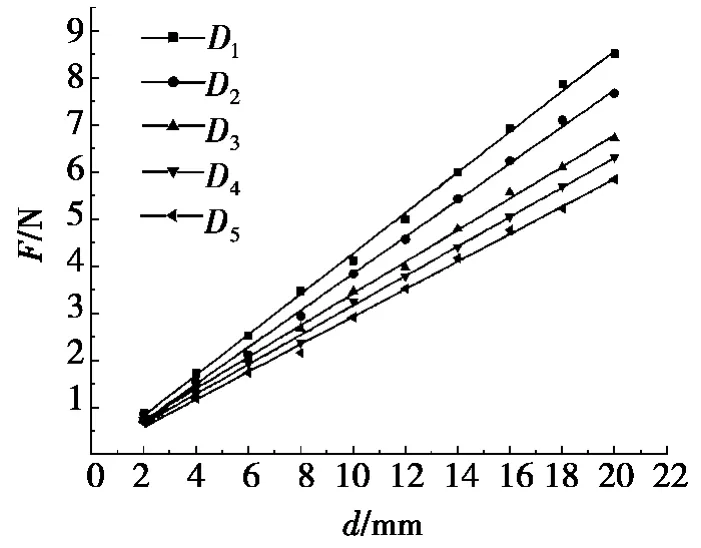
图7 偏心距与推力关系图

表4 线性回归结果数据
图8 为各尺寸轴承套圈的弹性变形量△L 与推力F 数据分布图,从图8 中可清晰得出:在本试验模型下,两者基本符合二次多项式关系,故将表1 中所有推力与变形量的数据以一条直线拟合,其拟合方程为:

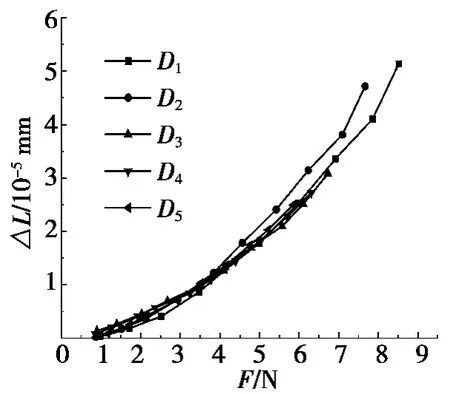
图8 套圈变形量与推力关系图
拟合数据结果中B0=-9.503 5 ×10-4,根据方程(4),当F 为0 时,△L 应为0,拟合曲线可决定因数为0.988 75。试验数据与实际情况相符合,误差较小。
经过试验及对其结果数据的分析可以得出:在使用旋转气场对轴承套圈进行定位且旋翼出口压力一定时,轴承套圈变形量与其所受推力呈上式拟合方程所表述的二次多项式关系,与轴承套圈直径无关。故对任意直径的轴承套圈进行定位时,由其所受推力大小即可求出其变形量。
4 结论
本文针对薄壁轴承检测的定位问题,设计了旋转气场自定位装置,并通过数值模拟分析了定位中造成薄壁套圈变形的因素,建立了弹性变形量与套圈直径、偏心距以及套圈受力的定量关系,最终得到使用该定位装置对任意直径轴承套圈定位的判定依据,套圈定位精度及变形量的计算公式。试验结果表明:通过旋转稳定气场实现薄壁轴承套圈自定位的方法是可行和有效的;本文所涉及的定位装置不仅可实现对被测薄壁轴承套圈的快捷定位,同时由于定位力仅使套圈产生弹性变形,保证了零件质量及测量精度要求。
[1] 张秀君.薄壁轴承的设计应用[J].轴承,1997(3):6-10.
[2] Rodrguez R A 公司.薄壁轴承[J].现代制造,2008(8):58.
[3] 陈白宁,赵明,任亚军.轴承外径非接触在线检测系统的研究[J].自动化仪表,2009(5):55-59.
[4] 刘海,任小中,张洛平.基于BP 神经网络的轴承套圈磨削误差的预报[J].河南科技大学学报:自然科学版,2006,27(2):13-15.
[5] 孙伟,韩建海,赵书尚,等. 轴承内径尺寸机器视觉在线检测技术[J]. 河南科技大学学报:自然科学版,2007,28(5):10-12.
[6] 薛明,李济顺,孙金花.薄壁轴承内外径气动测量装置测头的设计[J].轴承,2007(6):33-34.
[7] 伍开松,李明,余长柏,等.受局部内压管道外表面周向应力函数模拟[J].石油矿场机械,2008(12):42-44.
[8] 李彤,刘阿龙.基于MATLAB 的圆环承受均布压力分析[J].机械工程与自动化,2008(2):14-16.
[9] 刘小宁,张红卫,刘岑,等.钢制薄壁内压短圆筒静强度的试验研究[J].压力容器,2009(7):11-14.
[10] 杨增帅,袁玮,姚海兵.基于ANSYS 的内压薄壁圆筒壁厚计算有限元研究[J].中国高新技术企业,2009(8):9-10.
[11] 吴云峰.双向流固耦合两种计算方法的比较[D].天津:天津大学,2009:29-30.
[12] 沈栋平,郭波,王发峰.基于ANSYS 12.0 的静压轴承双向流固耦合分析[J].轴承,2012(7):7-10.
